含初始缺陷海底管道非线性屈曲失稳外压判别方法研究
王小龙,张 强
(东北石油大学 机械科学与工程学院,黑龙江 大庆 163318)
海底管道是海洋油气输运的主要工具,具有连续运作、输送量大、输送速度快和受气候影响小等优点,但海底管道在受到巨大的外部静水压力时仍然存在失效风险。这种情况下,海底管道有2种失效形式[1],一种是刚度不足导致的破坏,另一种是强度不足导致的屈曲失稳。在深海高压环境中,管道存在的任何微小缺陷都可能大幅降低管道的屈曲压力,引起海底管道的屈曲,而且海底管道直径与壁厚的比值(径厚比)通常大于20,其周向失稳通常发生在破坏之前。所以,失稳外压是海底管道计算时首要考虑的影响因素。
文中针对承受外压作用的某深水海底管道,采用有限元模拟方法,利用特征值屈曲分析的最大变形,构造管道初始缺陷,进行不同径厚比管道的非线性屈曲分析,提出了海底管道的临界外压判别的新方法。
1 海底管道外压失稳文献研究
针对海底管道失稳屈曲问题,国内外学者均有研究。Timoshenko[2]给出了均匀厚度的圆形薄壳受外压作用产生局部屈曲的平面应变经典解。针对含初始缺陷的海底管道,余建星等[3]研究了在弯矩和水压联合作用下的屈曲破坏问题,采用有限元法分别计算所受载荷在不同加载路径条件下的管道破坏形式。王泽武等[4]数值模拟了含缺陷海底管道横向屈曲,大量学者也对海底管道在高温高压下的屈曲进行了研究[5-9]。王品贤等[10]对国内外不同的管道设计标准中壁厚的计算方法进行对比并分析差异。冯胜等[11]对含腐蚀缺陷海底管道安全评价方法进行了比较。李牧之等[12]对真实工况下的海底管道进行数值模拟,并研究了管道初始缺陷对管道屈曲传播速度的影响。
这些研究涉及的研究方法普遍使用了特征值屈曲分析。特征值屈曲分析无法考虑真实结构存在的缺陷和非线性问题,但特征值屈曲分析可以为非线性屈曲分析提供参考[13]。当初始缺陷无法准确估计时,特征值屈曲模态可以作为几何缺陷的形状,故含几何缺陷的非线性屈曲分析更符合实际工程应用。
2 海底管道外压失稳线性屈曲分析
2.1 线性屈曲计算模型
海底管道失稳是指在深水条件下,海底管道承受的外部压力超过某一临界值时突然失去原有几何形状的现象。目前分析海底管道失稳最常用的方法是,应用有限元分析软件模拟计算海底管道屈曲载荷,用Timoshenko经典解验证模拟结果的可行性。有限元线性屈曲分析方法可以当作非线性屈曲分析的第一步来评估临界载荷,可以用来作为决定产生屈曲模型形状的设计工具,为设计提供指导。
特征值对应的临界外压载荷pcr可通过式(1)和式(2)得出。

式中,Ke为结构的弹性刚度矩阵;Kσ为应力刚度矩阵;λ为特征值;d为特征值对应的特征向量;p为均布外压,MPa。
2.2 海底管道结构模型
某单层管深水海底管道材质API 5L X65 MO SAWL,直径 D=270 mm,壁厚 t=9 mm,管道长度L=30D,管道两端固支,受均布外压p=18.92 MPa作用,管道模型示意图见图1。
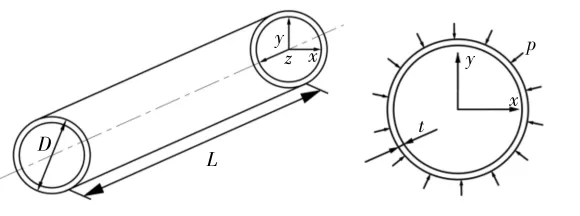
图1 单层管深水海底管道模型
2.3 线性屈曲模态分析
应用ANSYS有限元分析软件,分析单层管深水海底管道整体一阶线性及中间截面线性屈曲模态,结果见图2。
由图2可见,在均布载荷的作用下,管道发生屈曲失稳,海底管道整体变形十分明显。失稳后的管道变形对称,特征值λ=0.97。根据式(2),计算得到 pcr=0.97×18.92=18.35(MPa)。

图2 单层管深水海底管道整体一阶线性及中间截面线性屈曲模态
2.4 管道长度无关性验证
当管道长度L超过临界值,即管道足够长时,可以忽略长度对管道临界外压的影响。取D/t=30,用管道直径D的倍数表示管道长度L,模拟计算不同长度管道的临界外压pcr,有限元计算结果的拟合曲线见图3。
由图3可知,L小于30D时,误差较大,管长引起的临界压力变化不能忽略;L由10D加长至30D,pcr逐渐减小;L由 30D加长至 50D,pcr基本不变。因此,确定30D为管道的临界长度。
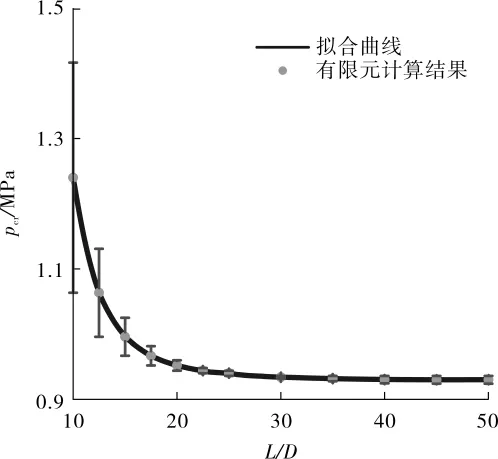
图3 不同长度管道临界外压有限元计算数据及关系拟合曲线
2.5 解析解与有限元结果对比
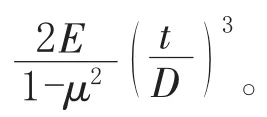
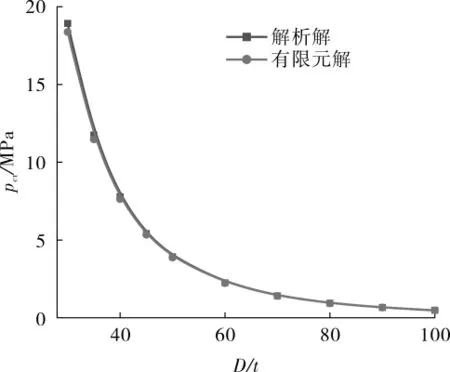
图4 不同长度管道临界外压解析解与有限元解对比
由图4可知,随着D/t的增大,pcr快速降低。当D/t为30时,解析解与有限元解的误差为2.9%;当D/t大于70时,解析解与有限元解误差几乎为0,误差值随D/t的增大而减小。
3 海底管道外压失稳非线性屈曲分析
3.1 非线性屈曲模型
对于受对称载荷的对称结构,可采取加扰动力的方法直接得到屈曲解,也可基于线性分析的屈曲模态间接得到屈曲解。间接法的做法是,将线性分析的一阶屈曲变形量乘以一个很小的系数,使整体结构具有初始缺陷,然后按照非对称结构求出非线性屈曲解。
本文中海底管道的非线性屈曲求解采用间接法,其中一阶屈曲变形量系数的确定条件为,变形量乘以系数后对应的管道缺陷值在0.1t~0.44t。以线性屈曲外压为非线性分析的施加载荷,研究管道缺陷对管道变形量的影响,以及不同径厚比的管道在不同缺陷情况下的临界屈曲外压的变化情况。非线性计算过程中,外压载荷随载荷步数的逐渐增加而增大,迭代过程不收敛时停止,不收敛前的某一阶载荷值即为非线性临界失稳压力。经过迭代计算得到管道整体一阶线性及中间某截面的非线性屈曲模态,见图5。
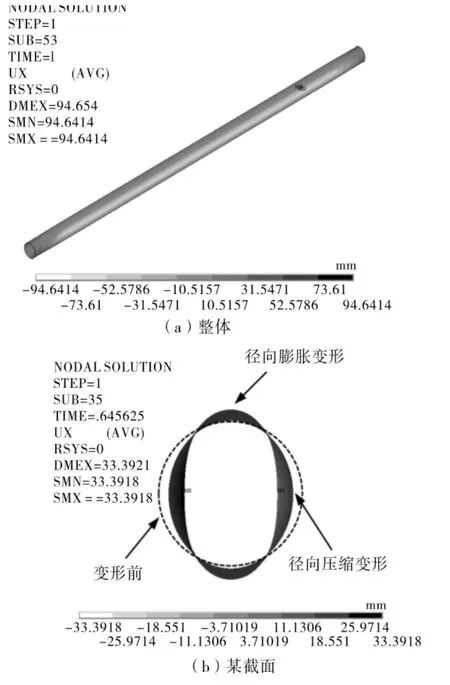
图5 单层管深水海底管道整体一阶线性及中间某截面非线性屈曲模态
3.2 几何缺陷对最大变形的影响
对海底管道进行非线性屈曲分析时,由于外压作用,在直径方向产生膨胀变形up和压缩变形us。有限元计算不同管道缺陷条件下外压载荷p对应的up、us,用计算数据绘制变量变化关系曲线,见图6和图7。
可以看出,图6和图7呈现的变化规律相似。当管道缺陷一定时,up、us均随着p的增大而变大,变化趋势为先缓慢后加快,相同条件下us>up。p相同时,管道缺陷越大,管道受外压后的up与 us越大。

图6 不同管道缺陷条件下管道膨胀变形与外压变化关系曲线

图7 不同管道缺陷条件下管道压缩变形与外压变化关系曲线
3.3 几何缺陷沿轴向变形分析
管道受到外压作用下,首先在局部产生径向变形,随着压力的增大,变形沿着管长方向传播。模拟计算了不同管道缺陷条件下管长L对应的up、us,用计算数据绘制变量变化关系曲线,见图8和图9。
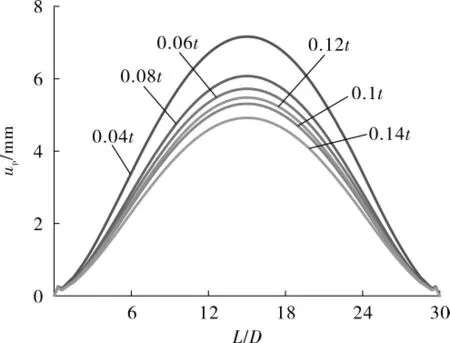
图8 不同管道缺陷条件下管道膨胀变形与管长变化关系曲线

图9 不同管道缺陷条件下管道压缩变形与管长变化关系曲线
可以看出,图8和图9呈现的规律相似。随着管长的增大,up、us逐渐增大,管道两端固定约束,径向变形量为0,变形量在管道中部达到最大。相同缺陷条件下,up>us。
4 海底管道失稳外压判别方法研究
4.1 文献方法
参考文献[14-15]中的方法,对有缺陷的管道进行非线性屈曲分析。模拟计算不同管道缺陷条件下管道外压p对应的管道位移u。以u为管道变形量,将计算数据绘制相应的变化关系曲线,见图10。
由图10可知,当载荷达到一定值时,管道变形突然增大,即曲线的斜率突然增大。参考文献[14-15]中根据斜率突然增大将对应状态的外压判定为管道的临界外压,得到的临界外压是一个大致的压力范围。

图10 不同管道缺陷条件下管道变形与外压载荷变化关系曲线
4.2 拐点方法
本文提出准确判定到达临界外压的载荷步,即临界压力值的拐点方法。此法的基础是文中前述的管道受压分析,即管道受外压作用,在径向产生膨胀变形up和压缩变形us,并沿轴向传播,us大于up。基于有限元软件模拟计算得到的us和up数据,计算压缩变形us与膨胀变形up的比值,制了不同管道缺陷条件下外压载荷p与变形量比us/up的变化关系曲线,见图11。

图11 不同管道缺陷条件下管道变形比us/up与外压载荷p变化关系曲线
由图11可知,随着p的增大,us/up先是逐渐降低,低至某一临界值时突然变大,随后又逐渐增大,形成图中可见的拐点。到达拐点之前,压缩变形速率小于膨胀变形速率,拐点之后,压缩变形速率大于膨胀变形速率,但管道总体变形趋势一直呈现逐渐压瘪的状态。到达此拐点之后,相对于膨胀变形,压缩变形表现为突然增大,因此将图中的拐点压力定义为临界压力值。
图11还表明,管道的缺陷越大,曲线越早出现拐点,即临界外压越小。
4.3 拐点法应用
应用本文提出的拐点法,取径厚比D/t在30~100的深水海底管道,研究了在不同缺陷情况下的临界外压,结果见图12。
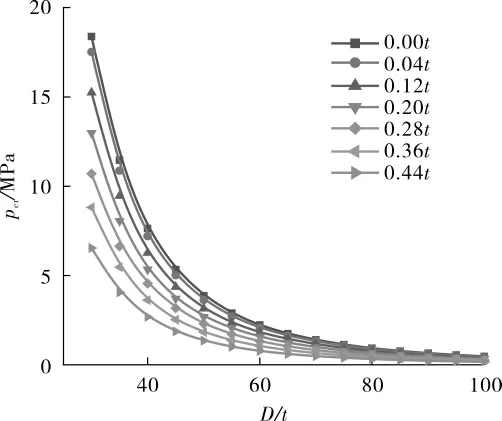
图12 不同管道缺陷情况下海底管道径厚比D/t与临界外压pcr变化关系曲线
由图12可知,随着D/t的增大,临界外压pcr逐渐减小。当D/t从30增加到40,pcr降低了58.46%。同一D/t情况下,管道的缺陷越大,对应的pcr越小。当D/t为30,管道无缺陷时,pcr为18.375 MPa;管道缺陷为 0.04t时,pcr为 17.517 MPa;当缺陷增大为0.44t时,pcr为6.54 MPa,降低了62.66%。
5 结论
(1)受外压含初始缺陷海底管道的非线性屈曲过程中,径向方向会产生膨胀变形和压缩变形,压缩变形大于膨胀变形。变形在管道中间部分达到最大,沿管长方向传播,变化速率为先慢后快。
(2)取压缩变形与膨胀变形的比值,分析了二者的比值随管道外压的变化趋势。研究发现,随着外压的增大,比值先降低到最低点,然后逐渐增加,曲线出现明显的拐点。将比值达到最低点的压力,判定为管道非线性屈曲的临界外压。
(3)应用上述判断管道临界外压的方法,分析了不同径厚比海底管道的临界外压。管道的临界外压随着径厚比的增大而减小,径厚比是影响海底管道临界外压的重要因素。对于同一径厚比的管道,其承压能力随着管道缺陷的增大而减小。

