借助“一题一课”建构数学概念复习课
王闻 李克民

[摘 要] 文章借助“一题一课”建构数学概念复习课,引领学生理性回归课本,梳理数学概念;画图叙事,运用图形直观辨析数学概念;叙事画图,在问题中加深对数学概念的理解;融合数学活动,增强数学概念的应用性,提升学生正确运用数学概念分析问题和解决问题的能力.
[关键词] 一题一课;数学概念;深度思维;复习课
“一题一课”是指教师对一道典型题或一项学习材料进行深入研究,挖掘其内在的学习线索与资源,科学有序地组织学生开展学习活动,激发学生深度思维,从而完成一节课的教学任务.
数学概念是学生学习数学的根基,学生只有掌握数学概念的本质,了解数学概念产生和发展的过程方能厘清数学概念之间的关联,继而引发学生的深度思维,才能正确运用概念解决问题.
在中考数学复习的过程中,笔者发现许多学生在遇到与“距离”有关的试题时容易出错,究其原因是学生没有厘清与“距离”有关的数学概念的本质与关联. 于是,笔者围绕与“距离”有关的数学概念展开“一题一课”的概念复习课设计. 借助“一题一课”建构数学概念复习课,引领学生学会剖析数学概念的本质,厘清数学概念的关联,能够提升学生正确运用数学概念分析问题和解决问题的能力.
理性回归课本,梳理数学概念
课本是最好的教材. 学生学会回归课本,理性地研究数学概念,对相似的概念进行类比分析,厘清知识间的脉络,可将知识“连点成线,织线成网”.
章建跃老师说,“对同类概念进行对比,可概括共同属性”. 教师让学生先到课本上找到“两点之间的距离”概念、“直线外一点到直线的距离”概念、“平行线间的距离”概念,结合生活实际说明距离的含义、点与点的距离含义、点与线的距离含义、同一平面内两条平行线之间的距离含义;接着,教师再引领学生联想与之相关的概念,如线段的垂直平分线的性质(判定)定理、角平分线的性质(判定)定理、三角形的外心内心、圆中的两条平行弦推论等;最后,教师引领学生画出与距离有关的“思维导图”,形成概念群,如图1.
通过思维导图让学生意识到线段垂直平分线的性质(判定)定理实质上指点与点之间的距离,而角平分线的性质(判定)定理是指點与线之间的距离,同一平面内两条平行线之间的距离指其中一条线上的任一点到另一条线的距离. 这样,学生能抓住以距离为中心的核心概念之间的关联,最终将其转化为点与点之间的距离和点与线之间的距离这两大类问题.
通过回归课本,厘清相似数学概念的本质及其关联,锁定不同概念之间的内在联系及不同表象之间的关联,在头脑中形成相关概念的网络,概括其共同属性,厘清其特性,有助于学生正确解决问题.
画图叙事,运用图形直观辨析
数学概念
画图叙事是指通过绘制图形来叙述一件事情. 这里的画图叙事是指通过画图来叙述数学概念、定理,运用数形结合的思想方法辨析数学概念,能让学生直观地感受到数学概念. 例如,在复习与“距离”有关的数学概念时,教师引领学生通过画图感受点到点的距离是指连接两点之间线段的长度(如图2)、点到直线的距离是指点P到直线的垂线段的长度(如图3)、平行线间的距离是指一条直线上的任意一点P到另一条直线的垂线段的长度(如图4),从而让学生理解垂线段的长度含义,能说出线段与垂线段的含义及功能. 接着,学生再通过画三角形的外接圆与内切圆,感受外心与内心的形成过程,并正确地叙述三角形外心与内心的特征. 然后,学生根据同一平面内两条平行线的距离解决圆中两条平行弦之间的距离问题,进而能得出圆中两条平行弦所夹的弧相等的推论. 这样,学生通过直观画图和具体操作能亲身感受数学概念的形成过程及定理(推论)产生的依据,就会对距离的概念有深刻印象和本质的认识.
例题:已知∠MON等于60°,E,F两点分别位于∠MON的两边上. 试在∠MON的内部寻找一点O,使点O到E,F两点的距离相等,且到∠MON的两边距离相等.
面对此题,学生就要根据题目的叙事画出图形进行分析,发现线段EF的垂直平分线和∠MON的角平分线的交点即为点O. 学生在叙事画图中切实体验了“到线段两端距离相等的点在这条线段的垂直平分线上”“到角两边距离相等的点在角的平分线上,这个距离是点与直线之间的垂线段的长度”,并能正确地解决问题. 画图叙事是渗透数形结合思想方法的桥梁,它能更直观地引领学生深刻地理解数学概念,让学生进入深度思维状态.
直观和具体是理解数学概念的重要方式和手段,教学中我们可以设计生动形象的数学实验解释抽象的数学理论,让学生真正理解数学概念的本质意义,增强概括与抽象能力. 直观和具体的画图叙事方式让学生有效地认清了数学概念的本质,并能运用数学概念解决问题.
叙事画图,在问题中加深对数 学概念的理解
图形语言是一种直观模型,简明扼要. 根据叙事能正确地画出图形等于学会了数形结合的思想方法,称之为叙事画图. 在解决数学问题时,学生如果能根据题目的意思(即叙事)正确画出图形,解决问题就变得更简单. 若想真正解决问题还需要学生有扎实的数学基础知识,尤其是运用数学概念解决问题的能力.
问题1:如图5,OP平分∠MON,PA⊥ON于点A,Q是射线OM上的一个动点,若PA=2,求PQ的最小值.
教师先引领学生用自己的语言叙事,通过问题分析和直观地画图发现当PQ为垂线段时才有最小值,从而用角平分线的性质定理求出PQ的最小值是2.
问题2:如图6,点A在∠MON的OM边上,点B在∠MON的内部,点D是边ON的一个动点,当点D在何处时使得点D到点A、点B的距离之和最小?
这道题既加深了两点之间距离的概念,又巩固了典型的几何求最值的方法. 这要求学生运用轴对称的性质将问题转化为两点之间线段最短问题,进一步提升学生运用数学概念解决问题的能力.
问题3:如图7,点A在∠MON的OM邊上,点B在∠MON的ON边上,点D是ON边上的一个动点,点E是OM边上的一个动点,当动点D,E在何处时使得AD+DE+BE的和最小?
这道题是由上题的一个动点改编成两个动点,难度又增大很多,要求学生从部分开始先考虑AD+DE的最小值,转化为两点之间线段最短问题. 需要先找定点A关于直线ON的对称点A′,再找A′E+BE的最小值,此时动点E在OM边上,点A′与点B是在OM同侧的两个定点,再找点B关于OM边的对称点B′,即可又转化为两点之间线段最短问题. 教师要引领学生学会多个动点问题的处理方法,把陌生问题逐步转化为熟悉的情境,再加以归纳总结,问题便可迎刃而解.
在画图的过程中,教师要引领学生学会思考与分析数学概念,学会在变式训练中引发深度思维、碰撞灵感、总结思想方法和技能,形成基本的数学活动经验,学生才能正确地运用数学概念解决实际问题.
融合数学活动,增强数学概念
的应用性
数学概念起源于问题又应用于问题解决. 近年来,与数学活动有关的中考题也越来越多,其中平移、翻折、旋转等图形变换是中考的热点问题之一. 学生要在日常学习中经历图形的运动变化,并在变化过程中积累操作经验,学会运用数学概念解决问题.
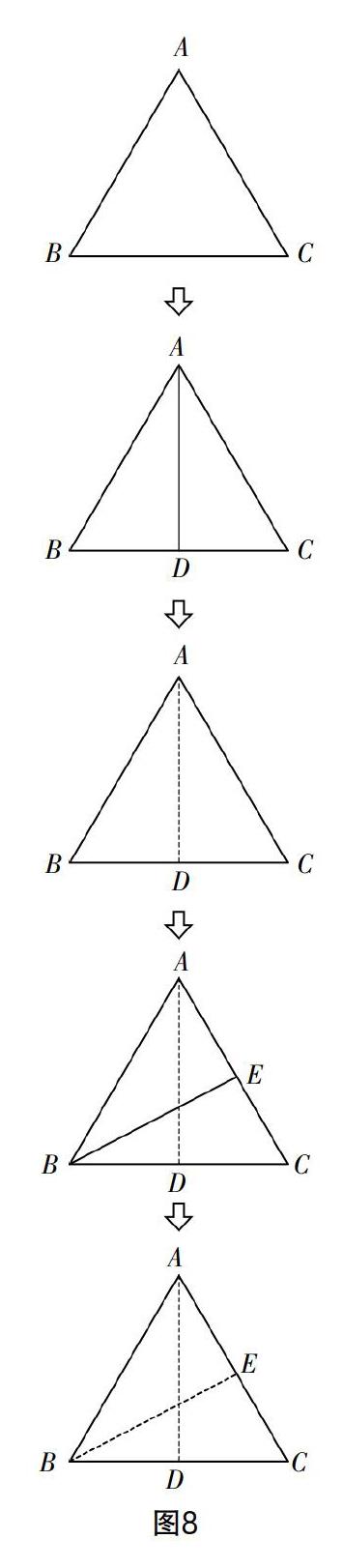
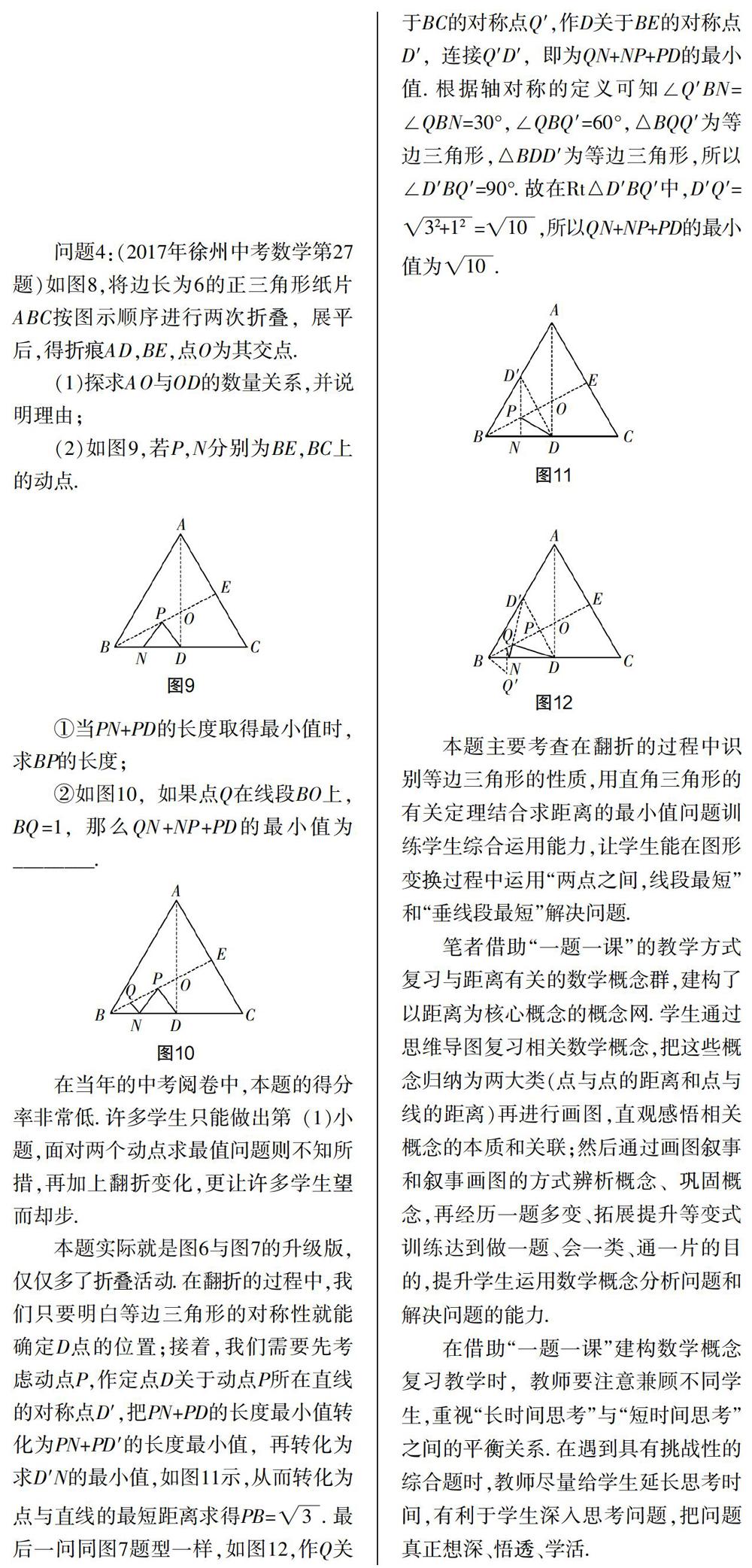
问题4:(2017年徐州中考数学第27题)如图8,将边长为6的正三角形纸片ABC按图示顺序进行两次折叠,展平后,得折痕AD,BE,点O为其交点.
(1)探求AO与OD的数量关系,并说明理由;
(2)如图9,若P,N分别为BE,BC上的动点.
①当PN+PD的长度取得最小值时,求BP的长度;
②如图10,如果点Q在线段BO上,BQ=1,那么QN+NP+PD的最小值为________.
在当年的中考阅卷中,本题的得分率非常低. 许多学生只能做出第(1)小题,面对两个动点求最值问题则不知所措,再加上翻折变化,更让许多学生望而却步.
本题主要考查在翻折的过程中识别等边三角形的性质,用直角三角形的有关定理结合求距离的最小值问题训练学生综合运用能力,让学生能在图形变换过程中运用“两点之间,线段最短”和“垂线段最短”解决问题.
笔者借助“一题一课”的教学方式复习与距离有关的数学概念群,建构了以距离为核心概念的概念网. 学生通过思维导图复习相关数学概念,把这些概念归纳为两大类(点与点的距离和点与线的距离)再进行画图,直观感悟相关概念的本质和关联;然后通过画图叙事和叙事画图的方式辨析概念、巩固概念,再经历一题多变、拓展提升等变式训练达到做一题、会一类、通一片的目的,提升学生运用数学概念分析问题和解决问题的能力.
在借助“一题一课”建构数学概念复习教学时,教师要注意兼顾不同学生,重视“长时间思考”与“短时间思考”之间的平衡关系. 在遇到具有挑战性的综合题时,教师尽量给学生延长思考时间,有利于学生深入思考问题,把问题真正想深、悟透、学活.

