数学课堂教学践行学科育人理念的探索

韦艳君

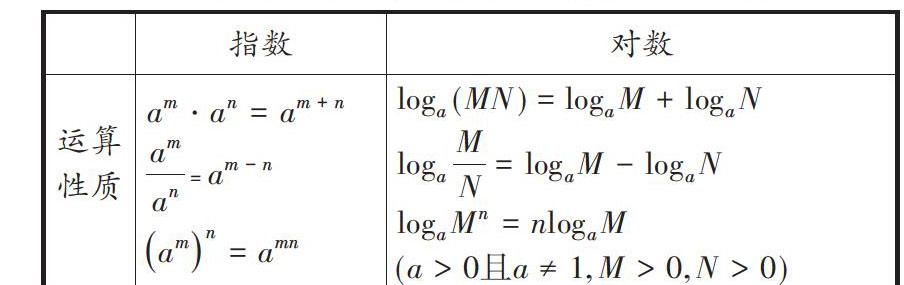
[摘 要]数学学科育人及数学核心素养的培养高度契合，在高中数学课堂教学中育人，即是对学生关键能力及必备品格的培养.在对数的概念与对数运算性质的教学中融入对数发展史，引导学生学习数学家克服困难、勇于创新的科研精神就是在教学中践行学科育人的有效途径.

[关键词]学科育人;数学课堂;对数

高中数学教学要注重培养学生的关键能力和必备品格，解答“培养什么样的人”的问题.习近平总书记在全国教育大会上强调“全面贯彻党的教育方针，把立德树人融入教育各环节中”，指导我们怎么培养人.育人是一种过程，贯穿于数学教学的始终.育人，是培育具有良好的政治素质、道德品质、科学思想等综合能力的人.数学学科育人，渗透在数学教学中，能潜移默化地培养学生的关键能力，塑造其品行.下面笔者以《对数与对数运算》教学为例，谈谈具体做法.

一、教学背景

《普通高中数学课程標准》指出，数学课堂教学应“努力揭示数学概念、结论发展过程，体会蕴含在其中的数学方法，追寻数学发展的历史足迹，把数学的学术形态转化成学生容易接受的教育形态”.高中数学人教A版中，对数概念的引入是由指数入手的.虽然承接了前面知识的学习，但对数的发现早于指数这一历史实际并没能有所体现.高中数学的学习，时间紧任务重，如何在一节课40分钟内完成对数概念的形成及对数性质的生成，是很多教师都在思考的问题.笔者尝试将数学史融入对数概念及性质的教学中，让学生体会学习对数的必要性和重要意义，从而激发探索的欲望.教师带学生回溯数学家艰难而漫长的对数研究之路，学习数学家克服困难、锤炼意志、勇于创新及挑战的科研精神和高尚品质，让学生在学习数学史料中自主合作探究对数的运算性质，感悟对数在运算化简中发挥的重要作用，感受转化与化归、数形结合、类比、从特殊到一般的数学思想，从而提升学生数学抽象、运算素养.笔者的教学设计旨在发挥数学学科的育人功能，落实数学核心素养的培养，培养德、智、体、美、劳全面发展的社会主义建设者和接班人.

二、教学过程

师：下面，我们一起来追溯对数产生的历史.古希腊时期阿基米德曾经发现几个10的乘方及10的个数之间的关系，我们用表格表示如下：

师：阿基米德发现规律之后并没有继续往下研究，错失了发明对数的机会.十五、十六世纪欧洲在航海、贸易、天文等方面发展迅速，在天文上的计算，经常要花上几天和半个月，计算难度比较大，人们迫切希望解决这一实际问题.十五世纪法国数学家许凯在以下双数列表中也发现了规律，并准确提出了数列中的乘、除、乘方、开方运算法则.

问题4：你能进一步发现双数列表中的乘、除、乘方、开方运算吗？

学生小组合作讨论，得出指数运算的相关结果.

师：受上述所发现的规律的影响，英国数学家纳皮尔研究了二十多年的时间，于1614年出版《奇妙的对数定理说明书》，对数就此诞生.纳皮尔将[ax=N]中的[x]称为以[a]为底N的对数.十七世纪，笛卡儿发明了幂的记号，指数概念才应运而生.因此，历史的长河里，先发明了对数，才有指数.随后，欧拉发现了指数与对数之间的联系，并创造了对数符号“[logaN]”，因此才有现在的对数概念.

设计意图：M·克莱因认为：“课本中的字斟句酌的叙述，未能表现出创造过程中的斗争、挫折以及在建立一个可观的结构之前，数学家所经历的艰苦漫长的道路.而学生一旦认识到这些，他将不仅获得真知灼见，还将获得顽强地追究他所攻问题的勇气，并且不会因为他自己的工作并非完美无缺而感到颓丧. ”追溯对数知识发展的漫长历程，让学生真实感受对数的来之不易，学习数学家开拓创新，对科学执着追求的品质.通过观察、归纳、猜想，由特殊到一般发现规律，初步认识对数对化简运算的重大作用及其必要性，激发学生的求知欲和创造欲，为对数运算性质的探索做好铺垫.以史育人之品德及坚韧意志，培养数据分析、数学运算素养.

问题5：能否在数学家的启发下，借助指数式与对数式的等价关系，研究对数的性质及运算性质？

设计意图：以对数发展史作为铺垫，强调指数式与对数式的关系的基础上，明确方法，为对数的性质与运算性质的探究提供思路.探究的过程，也是对对数概念的熟悉、领悟过程.

活动一：对数性质的探究

师生活动：教师提供指数中的性质[a0=1]，[a1=a]，让学生写出对应的对数，从而得出对数恒等式：[logaa=1]，[loga1=0]，并得到真数和对数的范围.

设计意图：熟悉对数定义中将指数式化为对数式的转化思路，深化对数的概念理解，同时为对数运算性质的探究做好铺垫.

活动二：对数运算性质的探究

师生活动：教师给出指数的运算性质，希望学生对应地得出对数的3种运算性质，并研究证明.

[ 指数 对数 运算性质

学生可能从以下方式来研究对数的运算性质.

（1）受数学家双数列表的启发，引入对数的运算符号，先发现一些特殊的对数运算关系，由特殊到一般，归纳猜想出对数的运算性质;

（2）紧紧抓住指数与对数的对应关系，由运算结构类比，抓住指数式中的指数就是对数式中的对数，指数式中的幂就是对数式中的真数这一联系猜想结论;

（3）通过指数式与对数式的关系，用符号表示对数，将对数化为指数，利用指数运算性质得出结论.

师：对数是苏格兰数学家纳皮尔在研究天文学的过程中，为了简化其中的运算而发明的.同学们从这三条运算性质有没有体会到“对数”对于简化运算的作用？

生：对数运算中，化乘为加，化除为减，化乘方为乘法，实现大数化小数运算.

设计意图：设计两个探究活动，让学生亲历对数恒等式及运算性质的生成过程.学生不断回归定义，由具体到抽象，深入“思辨”，多角度、多方位、多层次进行探索，锻炼学生思维的广阔性.

环节四：应用探究

师：以10为底的对数叫作常用对数，简记为[log10N=lg N].在物理、化学、建筑学等自然科学中还经常用到以e（e=2.71828…）为底的对数，叫作自然对数，简记为[logeN=ln N].

师：数学史上，人们经过大量的探究，制作了常用对数表和自然对数表，只要通过查表就能求出任意正数的常用对数或自然对数，现在还可以用计算器或计算机计算这两个对数值.

问题7：[logab=]？能否转化为以c（[c>0且c≠1]）为底的对数？

设计意图：利用转化与化归思想，对指对数互化知识进行再巩固，用所学的数学知识、思维方式和形式去解决实际问题，在实践中树立战胜困难的信心，体会知识的应用价值，促进学生创新性思维的发展.

环节五：归纳小结

问题8：请从知识、思想方法、课堂体验等方面谈一下你的收获和体会.

师生活动：

（1）知识：对数的概念、性质、运算性质;

（2）思想方法：转化与化归、数形结合、类比、特殊到一般等;

（3）情感体验：对数发展的艰辛历程，科学家坚持不懈、勇于探索的精神，合作探究中对指对互化的深刻理解.

设计意图：小结环节是一节课中的升华，促进学生从知识脉络、重难点、思想方法、情感体验等方面对学习过程进行总结，提高学生总结概括能力，锻炼学生对知识的表达能力.

三、教学反思与改进

这是笔者第一次尝试将对数的概念及性质合在一节课里教学，其合理性有以下几点.

（1）对数的概念及性质始终由“指对互化”展开，因此，同时对概念及性质的研究，本质是对指对互化思想的再三强调，有利于学生把握对数的基本知识，领悟处理指数与对数的基本技能.

（2）对数及其运算性质的产生与发展是数学家们无畏艰难，对科学执着追求，积极探索与创新得来的成果，课堂中重溯历史，有助于培养学生的科学研究精神、高尚品德及坚韧意志.

（3）对数定义及概念的探究，以问题为导向，环环相扣，层层推进.尤其对对数性质的证明，紧紧围绕指对互化展开，可以由特殊到一般归纳猜想，也可以用转化与化归思想、类比思想进行解决.研究的过程是数学抽象、运算素养的形成过程.

因此，本节课是在数学课堂中落实“立德树人”目标的优秀载体.但本节课也有一点不足，对数就高一学生而言，是一个全新的概念，接受能力比较弱的学生不能及时抓住核心——指对互化，就对对数性质的探究会比较吃力.关于这点，教师可以在上新课之前布置学生做好课前预习工作加以改善.

[   参   考   文   献   ]

[1]  刘灿文，杨懿荔.将数学史与数学本体知识巧妙融合：“对数概念及其运算”教案生成过程[J].数学学习与研究，2020（4）：116-118.

[2]  殷伟康，唐洁琼.数学史融入高中对数概念教学中的实践与思考[J].中学数学研究，2016（4）：1-4.

[3]  黄河清.构建学科育人模式的实践探索：以數学学科为例[J].广西教育，2021（8）：37-39.

（责任编辑 黄桂坚）