立足问题知识考点探究破题解析视角

常燕

[摘 要]二次函数与直角三角形问题的突破存在一定难度，需要学生把握知识考点，灵活选用解法来构建解题思路.总体而言，可从几何、代数两大方向进行问题探究，充分利用直角三角形的勾股定理、斜率之积为-1的几何意义来解题.

[关键词]二次函数;直角三角形;勾股定理;斜率

【真题探究】

2020年江苏省徐州市中考数学的压轴题以二次函数与直角三角形为背景，其解析方法具有一定的代表性，下面笔者对其进行深入剖析.

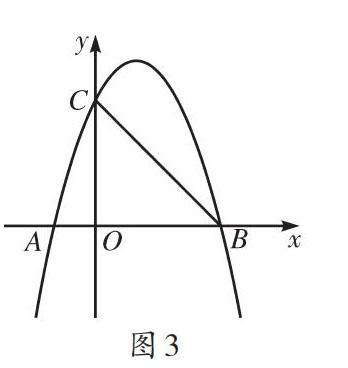
考题：（2020年徐州市中考数学卷第28题）如图1所示，在平面直角坐标系中，函数[y=-ax2+2ax+3aa>0]的图像交[x]轴于点[A]、[B]，交[y]轴于点[C]，它的对称轴交[x]轴于点[E].过点[C]作[CD∥x]轴交抛物线于点[D]，连接[DE]并延长交[y]轴于点[F]，交抛物线于点[G].直线[AF]交[CD]于点[H]，交抛物线于点[K]，连接[HE]、[GK].

（1）点[E]的坐标为 ;

（2）当[△HEF]是直角三角形时，求[a]的值;

（3）[HE]与[GK]有怎样的位置关系？请说明理由.

解析：考题为二次函数压轴题，第（2）问探究[△HEF]为直角三角形时a的取值，下面主要探究该问的解法，不对第（3）问深究.该问涉及点E，有必要先求解（1）问中点E的坐标.

（1）点E是抛物线对称轴与x轴的交点，由抛物线的解析式可知其对称轴为[x=-2a2×（-a）=1]，则点E的坐标为（1，0）.

（2）该问设定了众多的相交条件，根据交点求法即可求出关键点的坐标，将其表示为与a相关的点坐标.探究[△HEF]为直角三角形时a的取值可采用代数法，由点坐标求线段长，分类讨论不同情形下由勾股定理构建的方程.

评析：上述在突破二次函数与直角三角形问题时采用了代数法，即利用两点之间的距離公式求解三角形的边长，分三种情形讨论直角三角形，由勾股定理构建与坐标参数相关的方程，从而完成求解.该种方法的思维过程较为简单，但计算过程相对较为复杂，解析突破时需严格论证，精准求解.

【解法拓展】

对于二次函数与直角三角形问题，还可从几何视角构建解题思路，若坐标系中两直线相垂直，则直线的斜率之积为-1，具体原理如下.

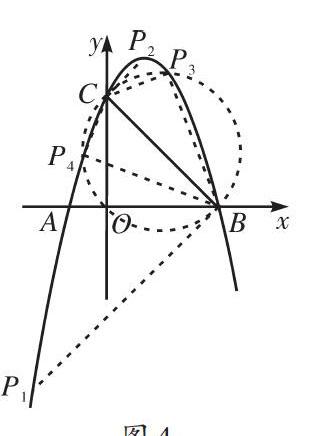
解析：上述为直角三角形探究题，点P为抛物线上的动点，题干没有设定直角顶点，则需要分别讨论点A、B和P为直角顶点的三种情形.可采用几何法，从斜率角度分别探讨.由于动点P位于二次函数图像上，可通过“两线一圆”来绘制图像，则具体步骤如下.

评析：上述在解析二次函数与直角三角形问题时采用了几何解析法，以相互垂直直线的斜率之积为-1来构建方程，然后分类求解点坐标.问题解析的难点主要在模型构建上，函数背景中特定条件下可构建不同的直角模型，会造成多解情形，此时就需要论证直角模型.合理利用几何圆的特性，利用隐圆建模是数学的常用方法，解题时可灵活运用.

【解后反思】

1.挖掘问题考查点，生成程序性解法

二次函数与直角三角形中考压轴题的设问形式较为多变，但考题所涉及的内容是固定的，知识考点有规律可循.往往考题涉及的知识点包括抛物线与直线的交点坐标、直线解析式、勾股定理、三角形相似的性质、两线垂直条件等.可综合运用函数与方程思想、数形结合思想、分类讨论思想来破解问题.教学中教师可引导学生深入挖掘考点，总结类型问题的解题思路，如二次函数与直角三角形问题可按照“设点找点→分类建模→构建方程→解点求值”的流程突破，教师可结合具体问题，帮助学生生成程序性解法.

2.挖掘解法原理，深入拓展探究

上述对二次函数与直角三角形问题开展解法探究，生成了代数法与几何法两种解题方法，每一种方法背后都隐含着对应的数学原理，因此深入挖掘解法原理是教学的关键.教师可立足基本问题引导学生理解几何法中利用斜率乘积构建思路的几何意义，以及代数法中由勾股定理构建方程的本质内涵，从而使学生从根本上掌握解题方法.另外，教师有必要对类型问题的解法进行拓展探究.以上述问题为例，除了利用勾股定理和斜率之积来构建思路，还可利用几何相似，通过直角三角形相似来挖掘垂直关系，求解推导.

3.关注思维发展，设问引导探究

考题探究是提升学生解题能力的重要方式，而在探究过程中应重点关注学生的思维活动，以发展学生思维为目的.如上述考题教学中有必要立足考题结构，引导学生思考问题考查点，结合图像进行条件推理，思考解析方向.教师在探究环节要合理设问，准确把控探究方向，启发学生思考，同时可引导学生适度联想，对比解题方法，有意识地培养学生思维的连续性.

（责任编辑 陈 昕）