考题追本溯源，由习题走向中考

李明莉

[摘 要]对考题开展追本溯源有助于理解问题，发掘结论.中考几何探究题往往与教材的习题、模型、结论有着一定的关联，深入探究可显著提升解题能力，发展数学思维.文章以一道中考几何探究题为例进行考题溯源、解法探究，并开展教学反思.

[关键词]习题;几何;相似;模型;探究

教材是知识的本源，习题具有强化知识、引导方法的作用.历年的中考压轴题往往“根”源于教材习题，深入研读习题可以获得典型问题的解题思路.因此考题教学中，有必要深入探究考题，对考题进行追本溯源.下面以一道2020年中考压轴题为例进行具体探究.

一、考题呈现

评析：本题为几何探究题，以“基础巩固→尝试应用→拓展提高”的形式引导学生探究，题目所涉三个小问既相互独立又存在关联.理解“基础巩固”环节问题的结构和解法思路对于后续问题的探究极为关键.

二、考题探究

1.问题溯源

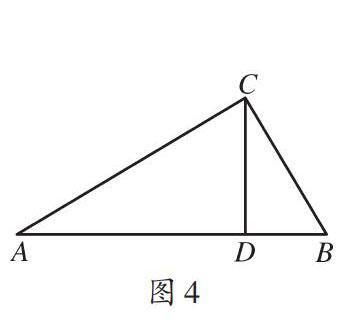
第（1）问，设定[△ABC]的[AB]边上的一点为D，与C相连后形成三个共边共角三角形：[△ABC]、[△ADC]、[△BDC].分析图形结构发现，问题源自人教版教材九年级下册第36题的习题2，其内容如下.

虽然考题与习题的条件存在差异，但本质上是一致的，图像所涉三个三角形是相似关系，以第（1）问证明为例，过程如下：

实则在该相似模型中，还可以由相似性质转化出线段之间的乘积关系，由于[△ACD?△ABC]，则[ACAD=ABAC]，所以[AC2=AD·AB]，这也是上述考题“基础巩固”环节结论证明的思路方法.

2.问题解析

（1）参考问题溯源中习题的解析思路，要证明三线段之间的乘积关系，只需要证明[△ABC∽△ACD]，该对相似三角形存在一个显著特点：含有一个公共角、一条公共边，图形结构为初中数学常见的共边共角相似模型.

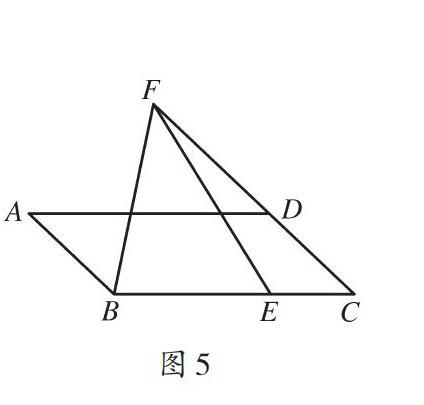
（2）该问依托平行四边形构建了与（1）问相似的共边三角形，问题突破还需参考上述模型的解析思路.具体突破时可进行图形分割，[EF]将[△BCF]分割为[△BFE]和[△ECF]，三者互为共边共角三角形.求[AD]的长，则可由平行四边形的性质进行等量转化，即[AD=BC]，则后续只需分析[BE]、[BF]和[BC]三线段关系即可，显然可将其转化为分析[△BFE]和[△BCF]的图形关系.参考上述问题，可知只需证明两者相似.

（3）该问以菱形为背景，求菱形的边长，根据上述问题突破的思路，显然需要在图形中构建共边共角相似模型，然后利用相似性质进行比例关系转化，进而求出线段长.注意到条件[EF∥AC]，则可分别延长[EF]和[DC]，设两线交点为G，如图6所示，则在[△DEF]中存在共边共角相似模型，具体求解过程如下.

3.问题评析

上述以探究的形式，依托共边共角相似模型构建了几何综合题，整体难度适中.第（1）问的基础巩固实则就是引导学生回顾教材中的共边共角相似模型，这也是整个问题突破的核心关键，掌握三角形相似比例变换是重点.后续两问所考查的侧重点略有不同，第（2）问侧重复杂图像中的模型提取，而第（3）问侧重模型的综合构建，上述突破过程充分利用菱形、平行四边形等基本图形的性质，有效实现问题转化.

三、解后思考

1.重视图像解析，追溯问题原型

中考几何探究题往往进行阶梯递进设问，图像结构由简单到复杂，充分理解图像、掌握图形特点是关键.因此在读题阶段要重视图像解析，必要时可進行问题溯源，思考问题在教材中的原型，从而联想解题思路，获得对应的解题策略，这也是中考几何探究题的重要考查方向.如上述几何探究题实则是对教材共边共角模型的拓展变式，利用相似模型的结论可直接获得关键条件，从而高效破解.在教学中，教师应重视教材经典习题的讲解，结合数学模型来引导学生掌握问题突破策略.

2.重视结论归纳，关注模型变化

几何探究题侧重考查学生提炼结论、总结归纳能力，即基于几何问题的条件、特征提取结论，形成问题的解析策略.如上述探究题中提取了共边共角模型，利用相似比例关系推导线段长，模型的结论是后续破解的基础.因此在探究教学中，要注重提升学生的总结归纳能力，引导学生掌握总结问题、归纳结论的方法，提升学生的数学能力.另外，归纳总结是建立在对模型的深层理解上，故教学中教师还应引导学生关注模型变化，从模型的一般性中获得特殊的结论，逐步提升学生的综合能力.

3.重视探究过程，发展数学思维

“经历探究过程，总结问题结论”是探究型问题的典型特点，即考题以探究形式引导学生思考，进行结论总结，强化应用.因此该类问题更为关注学生的思维过程，教学中教师要注重培养学生发现问题、猜想验证的能力，发展学生的数学思维，可结合具体内容开展探究活动，引导学生操作实践、独立思考.以上述几何探究题的共边共角模型为例，可首先展示习题，让学生思考问题图像的特点，然后讨论问题解析方法，总结并验证结论，在此基础上进行拓展探究，可以函数图像为背景进一步变式探究，帮助学生完成知识融合与思维完善.

四、写在最后

几何探究题往往注重对教材习题、模型、结论的挖掘，开展考题溯源，挖掘问题本源内容对于理解问题、总结方法有一定的帮助.教学中教师要注重引导学生关注教材，以教材为基础开展探究活动，针对性地提升学生的探究能力，发展学生的数学思维.

[   参   考   文   献   ]

[1]  李茂辉.解读几何探究，探讨解析思考：以一道几何探究题的思路突破为例[J].数学教学通讯，2020（11）：71-73.

[2]  刘媚.中考几何探究性问题研究[J].中学数学，2019（8）：87-88.

[3]  徐新.山重水复疑无路，柳暗花明又一村：谈一道中考几何综合题的命制过程[J].中学数学教学参考，2019（15）：57-58+74.

（责任编辑 陈 昕）