整体推进定序列 多元途径破难点
任宁 李亦儿
大概念视角下的单元整体教学,是基于学习者和数学核心概念的需求,对教材内容、教学资源重新进行优化与组合,以结构化的学习活动推进组织教学。我们以人教版数学教材四年级下册“运算定律”单元为例,重新梳理教学序列,关注学科内知识的整合,通过多元途径突破学习重难点,注重学生对大概念的理解和应用,以期达成学生整体素养的提升。
一、整体教学前置思考
(一)整体思维视野下的单元序列重组
国内教材关于运算定律单元编排有两种基本思路:一种是以运算形式为线索,先学习加法运算定律,再学习乘法运算定律;另一种是以运算律为线索,先学习交换律,再依次学习结合律、分配律。
人教版数学教材四年级下册“运算定律”单元是以运算形式为线索的。在实际教学过程中,学生研究完加法交换律后,很自然地会产生疑问:加法有这样的运算定律,那么其他运算中是不是也存在这样的定律呢?此时安排探究活动环节,学生容易通过迁移发现乘法交换律,这样的学习序列更符合学生的学习心理需求。基于这样的思考,本单元学习内容序列调整为:交换律—结合律—交换律、结合律的应用—分配律—分配律练习—减法、除法性质—运算律的应用—拓展(高斯求和、分配律)—整理与复习—综合练习。
(二)大概念指引下的单元整体教学思考
加法交换律和结合律的知识本质是加法的意义,而加法的源头实际上是自然数的计数。如“6+5=11”,就可以解释为“先数左边的6颗糖,再数右边的5颗糖,一共有11颗糖”,而“5+6=11”就可以解释为“先数右边的5颗糖,再数左边的6颗糖,一共有11颗糖”,所以“6+5=5+6”。这就是自然数计数原则中的顺序不相干原则。加法交换律和结合律对算法的侧重点不同,算理上的聚焦点都是相同的,即“加法运算结果与其运算顺序无关”。乘法是加法的简便运算,所以乘法交换律和结合律的本质也是乘法(加法)的意义,乘法分配律涉及两级运算,但其本质依旧是和乘法意义相关,乘法运算结果与其运算顺序也无关。
综上所述,贯穿运算定律单元的大概念就是运算意义(包括加法的意义和乘法的意义)。在运算定律教学中,乘法分配律本身的理解并不难,但因其变式较多,学生容易落入“一学就会、一做就错”的陷阱,因此成了单元学习的难点。剥去运算律的多重“外衣”,基于运算意义的底层逻辑帮助学生理解各个运算律特别是分配律及其变式的意义,突破学生的学习难点,是本单元教学的可取路径。
二、多元途径突破难点
(一)多元表征层层递进,丰富概念表象
人教版数学教材中用文字和字母两种方式对乘法分配律进行表征。为了让学生更好地识记、理解乘法分配律,教学中教师可以引导学生采用多元表征方式,多角度丰富对乘法分配律的概念表象。
教师出示:14×12的点子图及算式,长方形周长计算。
师:请同学们观察算式,你有什么发现?
生:第一题,我发现一种是分开来算,另一种是合起来算。
生:分开来算,就是先算10个14,再算2个14,最后相加;合起来算,就是把10个14和2个14合起来,等于(10+2)个14。
“分开来算”和“合起来算”,虽然不太严谨,但这是贴近学生认知水平的语言表征方式,教学中教师应该提倡学生用这种“不严密”的表达去理解抽象的数学概念。
教师出示两道算式:(1)(40+4)×25,(2)47×6+6×53。
师:说说你是怎么想的。
生:第(1)题,先用40与25乘,再用4与25乘。
师:你能上来用箭头表示一下,让别人看得更清楚吗?
(学生画箭头图,用25分别连接40和4)
生:第(2)题,我先把相同的因数6圈出来,放在括号外面,然后把47和53写在括号里。
画箭头、圈一圈等图示表征方式,能使学生更直观地记忆和理解乘法分配律的两种结构形态,结合之前的文字表征、字母表征、语言表征,帮助学生丰富乘法分配律的概念表象。
(二)多重理解反复穿行,促进概念理解
如果仅从识记结构的角度来看,学生无须花太多时间就能记住乘法分配律的“外形”。但是乘法分配律变式多,遇到结构不完整的就容易算错,且和乘法结合律容易混淆,如典型错例“26×99=26×(99+1)”和“25×(4×20)=(25×4)×(25×20)”。要更好地解答這类题目,仅仅记住结构是不够的,需要引导学生从乘法意义的角度去理解乘法分配律,用“几个几”来表述乘法分配律的两种表征形式的转换,从结构理解水平提升到意义理解水平。
教师出示问题:根据乘法分配律,在□里填上适当的数。
40×25+4×25=(□+□)×25
师:说说你是怎么想的。
生:把等式左边的相同因数25写在了右边括号的外面,那么“40+4”就应该写在括号里面。
师:你能解释一下吗?
生:等式左边表示的是40个25加4个25,所以右边就是(40+4)个25。
[教师出示:125×(40+8)=125×40+8]
师:你觉得这道题对吗?
生:不对。因为等式左边表示(40+8)个125,所以右边应该是40个125加8个125,合起来才是48个125,所以8后面要添上“×125”。
师:从合起来算到分开算我们要注意什么?
生:括号外的数要分别和括号里的两个数相乘,再相加。
教学中,结构理解和意义理解两种形式不可偏废,宜相互促进。当学生关注乘法分配律的结构形式时,教师要及时引导学生用“几个几”从乘法意义的角度进行解释。当学生用“几个几”表述乘法分配律的算式转换时,教师要引导学生关注算式“外形”的变化,促进学生对乘法分配律的真正理解。
(三)多向沟通适度拓展,注重思维提升
1.多重变式,提升思维层级
针对乘法分配律变式多、与乘法结合律容易混淆这一学习难点,需要在练习课中加强题组对比,利用“几个几”的乘法意义来沟通、突破。
教师出示两道算式:(1)25×(4+20),(2)25×(4×20)。
师:第(1)题大家都能做对,但是第(2)题有以下不同答案,你们同意哪个?
①25×4+25×20,②(25×4)×(25×20),③(25×4)×20。
生:第③个,因为它是80个25。
生:第①个是在算第(1)题。
师:这题能用乘法分配律吗?
生:应该用乘法结合律,用分配律的方法算出来的得数和原来的不一样。
师:乘法分配律和乘法结合律的式子看起来有点像,谁有什么好办法,让大家一眼就分辨出来吗?
生:括号里是加号的时候用乘法分配律,括号里是乘号的时候用乘法结合律。
生:乘法分配律的式子有4个数,而乘法结合律的式子只有3个数。
乘法分配律和乘法结合律“外形”类似,学生极易搞错。教师通过“计算原式得数、算式要素比较、运算意义理解”等多种途径,对两种运算定律进行区分,从而加深对乘法分配律的理解。
教师出示3道算式:(1)36×99+36,(2)36×99,(3)29×15+29×18+33×71。
生:第(1)题可以先在第二个36后面补上“×1”,这样就可以看做是99个36加1个36,然后提取相同因数36,就是(99+1)个36,算出来是3600。
生:第(2)题把99拆成100-1,然后把99个36转化成(100-1)个36,等于100×36-1×36,算出来是3564。
生:第(3)题要先把前面两组数进行合并,29×(15+18)=29×33,然后再和第三组数合并,29×33+33×71=(29+71)×33=3300。
本教学环节呈现了“需要补1”“两次提取相同因数”等乘法分配律的多种变式,依然可以引导学生以不变应万变,利用“几个几”的乘法意义进行解释。
2.算用沟通,使知识关联
乘法分配律并不是学生在四年级下册才第一次接触,两位数乘一位数笔算、长方形周长计算公式、相遇问题,都有乘法分配律的影子。
师:看,这是乘法口算和求长方形的周长(配图略)。你能看到乘法分配律吗?
生:12×3的口算,分开来算10×3和2×3,合起来就是12×3。
生:长方形的周长计算方法,可以是6×2+4×2,也可以是(6+4)×2。
郑毓信教授指出:基础知识不应求全而应求联。学习了乘法分配律之后,教师可以引导学生发现之前所学知识中隐藏的乘法分配律,感知知识之间的联系,激发学生学习的兴趣。
三、测查数据彰显实效
(一)解题能力明显增强
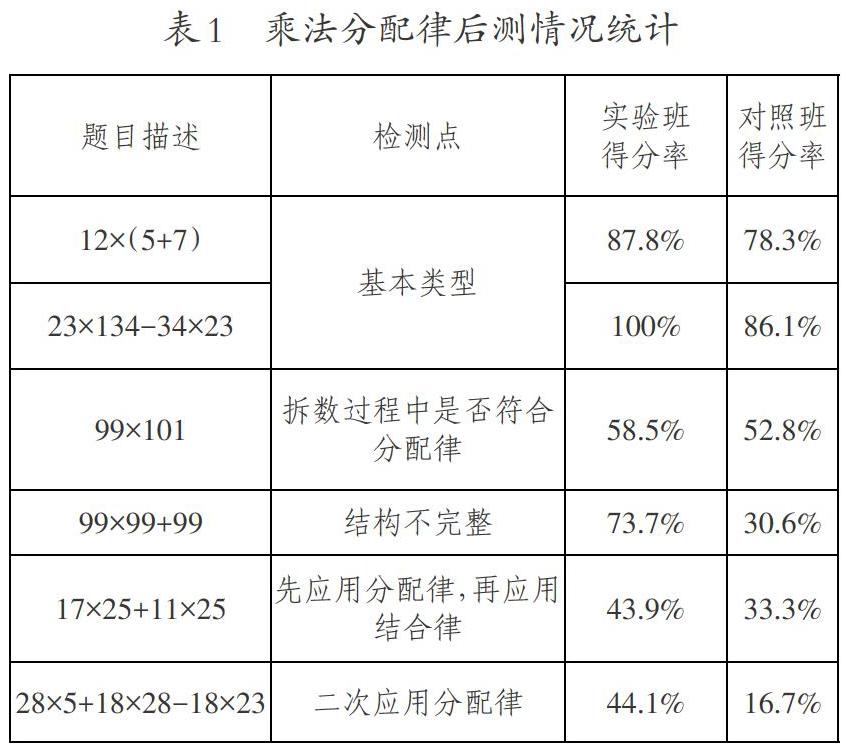
表1后测数据显示,对于基本类型的题目,实验班和对照班差异不明显。对于结构不完整或者其他变式的题型,实验班优势明显。
(二)深度理解概念内涵
对于“在我们学过的一些数学知识里,会存在乘法分配律的现象。你能举个例子,并进行解释说明吗?”这个问题,对照班只有5.6%的学生能回答,而实验班有24.4%的学生会以举例、文字描述、字母式的形式,对概念进行解释说明。由此可见,教学中教师提供丰富的乘法分配律相关素材,对学生深度理解概念起到了一定的作用。
乘法分配律概念内涵理解可以划分为三个层次:第一层次是概念性记忆水平,主要表征为识记结构,记住乘法分配律的多元表征形式;第二层次是说明性理解水平,主要表征为理解意义,能借助乘法意义对乘法竖式进行解释并执行运算;第三层次是探究性理解水平,主要表征为掌握概念内涵,能够把乘法分配律和长方形周长计算其他知识进行沟通。本课教学后三个层次水平的学生占比分别为20%、40%、40%,学生的理解水平呈现较好发展态势。
立足大概念的单元整体教學,要从提升学生核心素养出发,构建新的单元教学体系,以单元的视角发现儿童的认知结构与数学知识结构之间的关联,根据儿童的认知特征和实际水平改变教材序列,丰富数学概念的表征形式,使小学数学教学更具整体性、综合性和创造性,有效突破学习重难点,让学生真正理解知识的本质内涵。
(作者单位:浙江省宁波市奉化区锦屏中心小学浙江省宁波市奉化区居敬小学)
——特级教师周卫东《乘法交换律》教学赏析
——特级教师周卫东苏教版四下《乘法交换律》教学赏析

