抽丝剥茧探本源步步为营巧推断

李秀元 武刚

摘 要：探讨基于函数的复合方程根的四种求解类型，寻求问题的本质，形成解题模式，简化思维过程.

关键词：函数零点;复合函数;数形结合

中图分类号：G632      文献标识码：A      文章编号：1008-0333（2021）22-0039-03

收稿日期：2021-05-05

作者简介：李秀元（1973.11-），男，湖北省黄冈人，中学高级教师，从事高中数学教学研究.武刚（1976.1-），男，湖北省黄冈人，从事高中数学教学研究.

函数零点是高中数学一个重要概念.考查函数的零点，对于等价转化和数形结合思想方法培养有着非常重要意义.函数的零点，即函数图像与x轴交点的横坐标，也即对应方程的根.因此，基于函数的复合方程根的问题，最终将回归到基本函数的零点，研究基本函数的图像，從形上实现问题的求解.

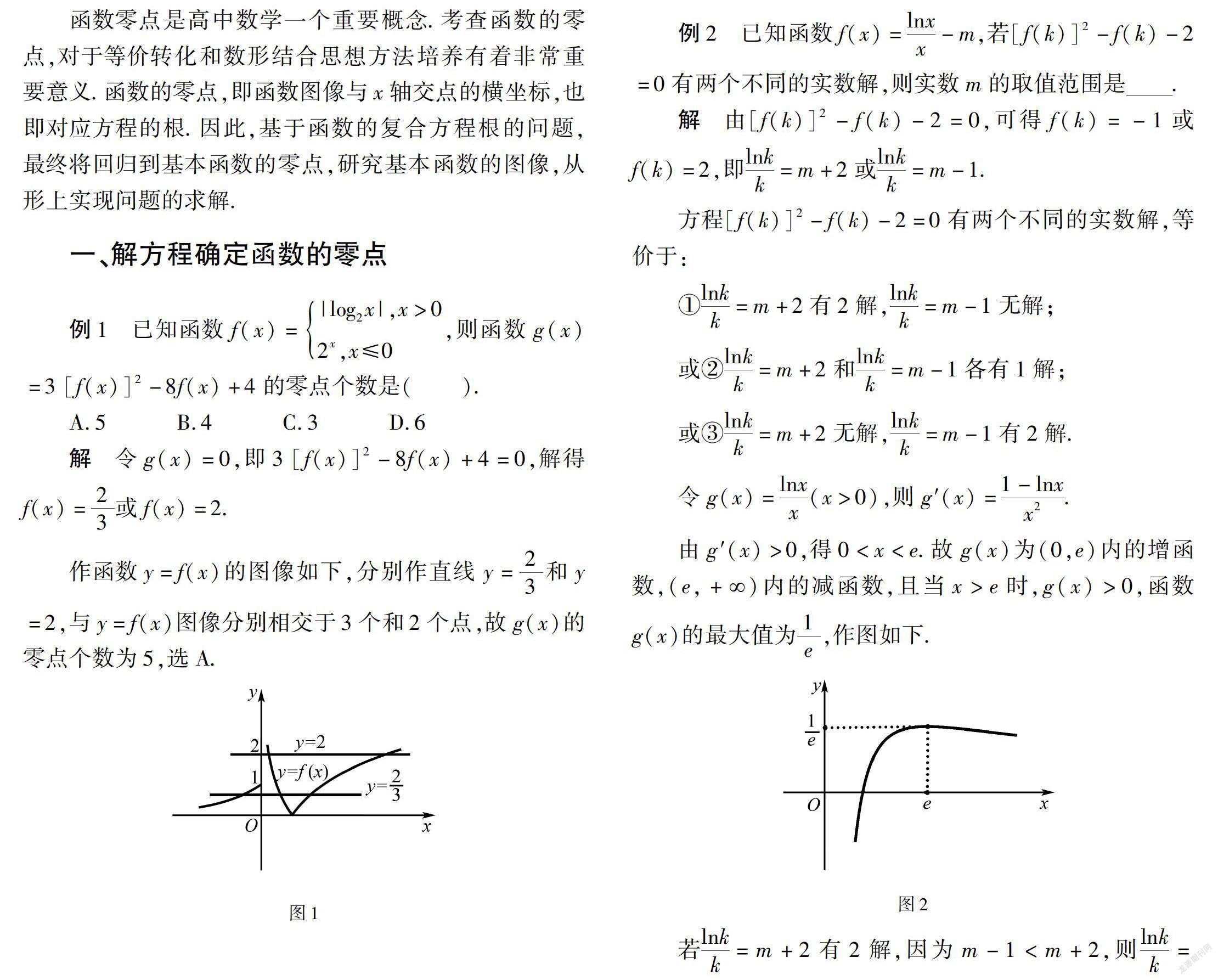
一、解方程确定函数的零点

评析 对于嵌套函数（方程），将f（x）换元后，原方程转化为方程组，但最终复合函数的零点是由f（x）=t来确定，而t的个数和范围直接决定方程f（x）=t解的个数.显然，函数y=f（x）的图像，在试题求解中依然起着举足轻重的作用.

参考文献：[1]李秀元，阮剑文.函数零点问题的处理策略[J].高中数学教与学，2018（13）：20-22.

[责任编辑：李 璟]