从物理模型建构分析高考物理试题
黄胜

摘 要:以2021年广东省普通高中学业水平选择性考试物理试题为例,针对试题中出现的生活实践问题情境和学习探索问题情境,呈现“基础性、综合性、应用性和创新性”四类物理模型建构特点和模型转换过程.引导教师从扎实基础模型、强化综合性和应用性模型以及关注科技的创新性模型的角度进行教学思考.
关键词:问题情境;模型建构;模型转换;高考试题
中图分类号:G633.7 文献标识码:B 文章编号:1008-4134(2021)15-0052-04
作者简介:黄胜(1987-),男,湖南湘潭人,硕士,中学一级教师,研究方向:高中物理教学方法及规律.
物理模型建构是物理核心素养中科学思维的重要组成部分,是学生根据研究问题和情境,在对客观事物进行抽象和概括的基础上构建易于研究的、能反映事物本质特征和共同属性的理想模型、理想过程、理想实验和物理概念的过程[1].模型建构是应用物理概念、规律和原理分析解决实际问题的关键步骤,是真实问题转化为物理问题的思维桥梁.2021年是广东省新高考模式的第一年,广东省普通高中学业水平选择性考试由省自主命题,绝大多数物理试题依托真实问题情境.笔者以2021年广东省普通高中学业水平选择性考试物理试题(以下简称为“2021年广东卷”)中的情境类问题及其中的模型转换方法为例,分享自己的经验及体会.
1 情境类问题
《中国高考评价体系》指出情境是实现“价值引领、素养导向、能力为重、知识为基”的综合考查的载体,是实现培养学生形成改造世界的实践能力的可行路径[2].而情境即为问题情境,是真实的问题背景.实际问题包含两类载体,第一类是生活实践问题情境:(1)大自然中的物理现象,如地球公转、雨后彩虹等;(2)与生产生活紧密联系的物理问题,以2021年廣东卷为例,如曲辕犁和直辕犁、车库出入口的曲杆道闸、赛龙舟、投掷手榴弹、算盘中的算珠、注射器抽取密闭药瓶中的药液等;(3)科技前沿,如我国自主研发的空间站“天和”核心舱、花瓣形电子加速器、银河系中的放射性同位素等.第二类是学习探索问题情境:物理学史问题情境、课程标准和教材中的典型问题情境、科学探究的问题情境,如测量缓冲装置中弹簧的劲度系数的探究问题等.物理情境往往结合自然现象、生产生活或科技应用,情境类试题以文字、符号和图形呈现实际情境,涉及的信息繁杂.考生需要在众多信息点中筛选有效的物理信息,关注实际条件、研究对象进行的过程等,综合应用分析与综合、抽象与概括、比较和分类、逻辑推理等思维方法,逐步将有效信息和物理情境转换为物理模型,进而分析求解.
2 模型转换
解决情境类问题的关键点和难点在于将问题情境转换为物理模型,常用的模型转换主要包括四种类型:(1)研究对象的转换;(2)物理状态和过程的转换;(3)条件的转换;(4)数学模型的转换[3].同一个物理情境中,往往需要经历多次不同类型的转换.一般模型转换的过程为:第一步选择合适的研究对象,形成对象模型;第二步分析对象所处的外部环境和运动过程变化,与已有信息(包括知识、方法、基础物理模型等)建立联系或寻找相似点,通过合理选择或综合应用、类比联想或抽象概括、原型启发或逻辑推理,形成新的状态和过程模型;第三步抓主要因素,忽略次要因素,借助数学模型进行计算、分析和讨论.下面以2021年广东卷为例,分析“基础性、综合性、应用性和创新性”物理模型建构中的模型转换过程.
2.1 基础性物理模型建构
基础性物理模型建构要求学生调动单一的知识或技能建构物理模型,载体为基本层面的问题情境.模型转换过程指向直接应用已知的基础物理模型.
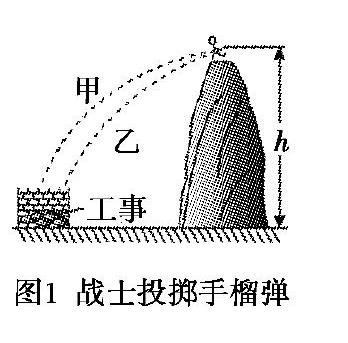
例题1 (第9题)长征途中,为了突破敌方关隘,战士爬上陡峭的山头,居高临下向敌方工事内投掷手榴弹,战士在同一位置先后投出甲、乙两颗质量均为m的手榴弹,手榴弹从投出的位置到落地点的高度差为h,在空中的运动可视为平抛运动,轨迹如图1所示,重力加速度为g,下列说法正确的有
A.甲在空中的运动时间比乙的长
B.两手榴弹在落地前瞬间,重力的功率相等
C.从投出到落地,每颗手榴弹的重力势能减少mgh
D.从投出到落地,每颗手榴弹的机械能变化量为mgh
物理模型转换:(1)对象模型:忽略手榴弹的形状和大小,视为质点;(2)物理运动模型:手榴弹水平抛出,运动模型为平抛运动;(3)条件的转换:忽略空气阻力,手榴弹仅受重力.
评析:物理情境为战士居高临下投掷手榴弹,根据平抛运动模型特点,竖直方向做自由落体运动,下落的高度相等,则下落时间相等.再根据功能关系分析重力势能和机械能的变化情况.使问题情境向物理模型转化的过程简单直接,不涉及过多的思维活动.
2.2 综合性物理模型建构
综合性物理模型建构要求学生在正确思想观念引领下,综合运用多种知识或技能建立物理模型,载体为综合层面的问题情境.模型转换过程指向通过综合选用多种基础模型后形成的新物理模型.
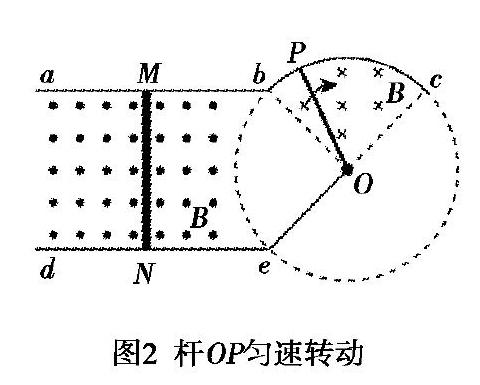
例题2 (第10题)如图2所示,水平放置足够长光滑金属导轨abc和de,ab与de平行,bc是以O为圆心的圆弧导轨,圆弧be左侧和扇形Obc内有方向如图2的匀强磁场,金属杆OP的O端与e点用导线相接,P端与圆弧bc接触良好,初始时,可滑动的金属杆MN静止在平行导轨上,若杆OP绕O点在匀强磁场区内从b到c匀速转动时,回路中始终有电流,则此过程中,下列说法正确的有
A. 杆OP产生的感应电动势恒定
B. 杆OP受到的安培力不变
C. 杆MN做匀加速直线运动
D. 杆MN中的电流逐渐减小
物理模型转换:(1)对象模型:金属杆OP和金属杆MN当作粗细均匀、接触良好、阻值恒定的导体;(2)物理过程模型:金属杆OP匀速转动,金属杆MN向左做加速度逐渐减小的加速运动,属于电磁感应中的双杆模型;(3)条件的转换:足够长且光滑的金属导轨,磁场区域分布的是匀强磁场.
评析:思维分析过程是金属杆OP转动—感应电动势EOP—感应电流I0—金属杆MN受到水平向左的安培力F—金属杆MN向左加速—感应电动势EMN—感应电流减小—安培力F减小—金属杆MN加速度减小,最终建构不同于常规双杆模型的新模型.模型建构中要求学生综合应用电磁感应、牛顿运动定律等多种知识能力,物理结果相互影响形成动态分析过程,对学生的逻辑推理能力要求较高.
2.3 应用性物理模型建构
应用性物理模型建构要求学生在正确的理念引领下,综合运用多种知识或技能建立物理模型解决生活实践中的应用性问题,载体为生活实践问题情境或学习探索问题情境.模型转换过程指向通过类比联想或抽象概括形成的新物理模型.
例题3 (第4题)由于高度限制,车库出入口采用如图3所示的曲杆道闸,道闸由转动杆OP与横杆PQ链接而成,P、Q为横杆的两个端点.在道闸抬起过程中,杆PQ始终保持水平.杆OP绕O点从与水平方向成30°匀速转动到60°的过程中,下列说法正确的是
A.P点的线速度大小不变
B.P点的加速度方向不变
C.Q点在竖直方向做匀速运动
D.Q点在水平方向做匀速运动
物理模型转换:(1)对象模型:转动杆OP的端点P和横杆PQ的端点Q,忽略杆的粗细,视作线状刚性杆(如图4);
(2)物理过程模型:P点绕O点做匀速圆周运动,Q点在竖直方向的运动与P点相同,水平方向的运动满足xQ=xP+lPQ;
(3)条件的转换:杆PQ始终水平,刚性杆两端P点和Q点的运动轨迹均为圆弧的一部分;
(4)数学模型的转换:设OP的长度为lOP,以O点为坐标原点,过原点与PQ水平的轴线为x轴,建立直角坐标系.设杆OP转动的角速度为ω,转动时间为t.则运动过程中:
评析:问题情境是由于高度限制而设计使用的曲杆道闸,横杆PQ保持水平的特点大大减小了道闸的总高度,符合情境的科学性和目的性,模型构建依托生活实践问题情境. P点绕O点做匀速圆周运动,则其线速度大小不变,加速度方向时刻指向圆心.Q点的竖直位移yQ=lPQ·sinπ6+ωt,不是匀速运动.Q点的水平位移xQ=lOP·cosπ6+ωt+lPQ,也不是匀速运动.
2.4 创新性物理模型建构
创新性物理模型建构要求学生在正确思想观念引领下,在开放性的综合情境中创造性地建构模型,创造性地解决问题,形成创造性的结果和结论.载体为开放性的生活实践问题情境或学习探索问题情境.物理模型转换指向通过原型启发或逻辑推理形成的创造性的物理模型.
例题4 (第14题)如图5所示是一种花瓣形电子加速器简化示意图,空间有三个同心圆a、b、c围成的区域,圆a内为无场区,圆a与圆b之间存在辐射状电场,圆b与圆c之间有三个圆心角均略小于90°的扇环形匀强磁场区Ⅰ、Ⅱ和Ⅲ.各区磁感应强度恒定,大小不同,方向均垂直纸面向外.电子以初动能Ek0从圆b上P点沿径向进入电场,电场可以反向,保证电子每次进入电场即被全程加速,已知圆a与圆b之间电势差为U,圆b半径为R,圆c半径为3R,电子质量为m,电荷量为e,忽略相对论效应,取tan22.5°=0.4.
(1)当Ek0=0时,电子加速后均沿各磁场区边缘进入磁场,且在电场内相邻运动轨迹的夹角θ均为45°,最终从Q点出射,运动轨迹如图5中带箭头实线所示,求Ⅰ区的磁感应强度大小、电子在Ⅰ区磁场中的运动时间及在Q点出射时的动能.
(2)已知电子只要不与Ⅰ区磁场外边界相碰,就能从出射区域出射.当Ek0=keU时,要保证电子从出射区域出射,求k的最大值.
物理模型转换:(1)对象模型:电子视为点电荷;(2)物理过程模型:电子在电场区域做匀加速直线运动,在匀强磁场区域做匀速圆周运动;(3)条件的转换:忽略磁场与电场的边界效应,认为边界绝对清晰.忽略相对论效应,电场区域为方向规律性变化的辐射状电场,磁场区域为匀强磁场;(4)数学模型的转换:电子的运动轨迹圆与Ⅰ区边界圆相切时,即为电子出射的临界轨迹.需应用数学几何关系,确定电子轨道半径.
评析:类比教材中回旋加速器的原理(如图6),花瓣形电子加速器的基本原理有着非常多的相似之处.均采用规律性变化的电场以保证每一次电子进入电场区域都被加速,在磁场中利用电子受到的洛伦兹力来巧妙控制和改变电子的运动方向.该模型是基于回旋加速器模型的创新模型,巧妙设计电磁场的大小和分布,实现电子在有限区域内的循环加速过程.电子运动轨迹的精妙设计和其与回旋加速器的共同之处正是此物理情境的精妙之处,学生需要在常规复杂原型问题的基础上获得启发,寻找物理过程和原理的共通之处,才能创造性地解决新的物理问题.
3 模型建构的教学启示
3.1 扎实基础模型
基础模型是模型建构的基石,质点、点电荷、轻绳、轻质弹簧等模型的建立过程需依托情境,以理解其抓住主要因素、忽略次要因素的条件及价值.平抛运动、匀速圆周运动等基本运动模型的特点和规律,需要学生经历观察生活实际—探究运动过程—分析运动特征—发现运动规律,切忌死记公式、题海战术.学生应认识到匀强电场、匀强磁场、光滑、足够长等条件对简化物理模型的意义,隐含条件需通过深挖有效信息获取.重视数学在解决物理实际问题中的应用,常用的代数和几何分析方法需要熟练掌握.
3.2 强化综合性及应用性模型
复杂物理模型中的运动过程往往由多个基础模型组合而成,找准多个过程间的联系点,如瞬时速度、能量变化等,可以快速组装综合模型.建模是基于真实情境的抽象过程[4],在培养学生应用性物理模型的建构能力过程中,教师应通过实物展示、视频、课堂情境再现等方式真实呈现物理问题情境,以真正领会建模思想的内涵,不断强化学生从自然事物中抽象和概括事物或事件关键特征的能力.通过拓展型作业[5]、研究性学习等方式,创造机会让学生应用物理知识解决一个或一类实际问题,重点培养学生主动将物理模型与生活实际相联系的意识.
3.3 关注科技的创新性模型
现代科学技术的发展日新月异,教师除了教好教材中固有的物理知识体系外,也应关注现代科技发展.以期获得灵感可以将了解到的科技知识,通过简化转化为学生可操作自制的趣味物理小实验、改编为开放性的情境类问题试题、分享现代科技成果提升学生学习物理的兴趣等.在日常教学中教师应避免就题讲题,备课时可多设计开放性的问题讨论、多角度多方法地分析同一物理过程、适当地进行问题情境的拓展和变式训练,逐步提升学生思维的灵活度、发散性和创新性.
参考文献:
[1]廖伯琴.普通高中物理课程标准(2017年版2020年修订)解读[M].北京:高等教育出版社,2020.
[2]教育部考试中心.中国高考评价体系[M].北京:人民教育出版社,2019.
[3]陈金忠.浅谈高考物理情境类试题中的模型转换[J].中学物理教学参考,2020,49(12):51-54.
[4]任配璐,張兵荣.2003版与2017版物理课程标准中物理模型及建模的比较研究[J].物理教师,2021,42(03):2-6.
[5]谭国武.高中物理拓展型作业设计的实践探索[J].中小学教材教学,2019(01):69-72.
(收稿日期:2021-06-12)

