以“作图”促理解 探“变化”提素养

钟文丽　万妍青

摘  要：几何是研究空间形式的科学，图形是其最主要的表征形式.“图形的变化”作为初中数学几何学习的重点内容之一，是培养学生直观想象、发展空间观念、提升逻辑思维能力的重要载体. 文章从“作图”的角度，对2020年全国各地区中考数学试卷中部分涉及“图形的变化”的试题进行评析，并基于几何作图视角通过观察问题、分析问题并解决问题，逐步完善学生的认知结构体系，对“图形的变化”知识的内在联系进行归纳、梳理，落实以逻辑推理为核心的思维发展，提升学生的数学学科核心素养.

关键词：图形的变化;几何作图;中考数学

一、考点概述

《义务教育数学课程标准（2011年版）》（以下简称《标准》）要求通过具体实例了解各种变化的概念，能借助图形探索几何变化后图形的性质，并能“运用图形的轴对称、旋转、平移进行图案设计”. 综观2020年全国各地区中考数学试题，在“图形的变化”专题有侧重对学生作图能力的考查的趋势，部分地区“图形的变化”部分的试题在灵活性和创新性上都颇具看点. 而作图能力反映的是学生的基本应用技能和合情推理能力，同时也是直观想象和逻辑推理核心素养的体现.

本文中选取的以作图为载体的“图形的变化”试题，考点主要体现在三个方面：（1）考查轴对称、旋转、平移三种图形变化的基本作图方法;（2）运用尺规作图法分析图形变化后的性质及特点;（3）助力“综合与实践”与“图形的变化”相关联的问题解决.

二、试题分析

1. 重视基础，考查基本作图，强化直观想象能力

“图形的变化”专题侧重对作图技能及图形性质的考查，经历对平移、旋转、轴对称的作图体验，在“观察—操作—归纳—应用”的过程中构建与此相关的知识经验，扎实作图技能. 同时，在理解“作图步骤”的过程中，将文字语言转化为符号语言和图形语言，提升学生的数学阅读理解能力，进而强化学生的直观想象核心素养.

例1 （山东·烟台卷）如图1，已知点[A2，0，][B0，4，C2，4，D6，6，] 连接AB，CD，将线段AB绕着某一点旋转一定角度，使其与线段CD重合（点A与点C重合，点B与点D重合），则这个旋转中心的坐标为_________.

分析：解决此题的关键是能够找到对称中心.

解：所作辅助线如图2所示，设旋转中心是点P，则P[4，2.]

【评析】此题已知两个对称点，要去寻找对称中心，可以借助尺规作图中作线段垂直平分线的方法，即两条中垂线的交点即为对称中心. 灵活应用中心对称的性质是解决此题的关键所在.

例2 （安徽卷）如图3，在由边长为1个单位长度的小正方形组成的网格中，给出了以格点（网格线的交点）为端点的线段[AB，] 线段[MN]在网格线上.

（1）画出线段[AB]关于线段[MN]所在直线对称的线段[A1B1]（点[A1，B1]分别为点[A，B]的对应点）;

（2）将线段[B1A1]绕点[B1]顺时针旋转90°得到线段[B1A2]，画出线段[B1A2 .]

分析：此题考查了轴对称和旋转对称的作图方法.

解：（1）图4中的线段A1B1即为所求.

（2）图4中的线段B1A2即为所求.

【评析】此题第（1）小题考查了轴对称作图的方法，即找出图形中的关键点，过关键点作对称轴的垂线，延长垂线，在垂线的另一端取相等的线段，得到对应点，其他关键点以此类推，连接所有对应点即可得到对称后的图形;第（2）小题考查旋转作图的方法，即找出图形中的关键点，连接关键点和旋转中心，将连线按要求的方向与角度绕中心旋转，在连线上截取相等的线段，得到对应点，连接所有对应点即可得到旋转后的图形. 此题是基本作图法最典型的呈现方式.

例3 （黑龙江·鸡西卷）如图5，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，[△ABC]的三个顶点[A5，2，B5，5，][C1，1]均在格点上.

（1）将[△ABC]向左平移5个单位得到[△A1B1C1]，并写出点[A1]的坐标;

（2）画出[△A1B1C1]绕点[C1]顺时针旋转[90°]后得到的[△A2B2C1]，并写出点[A2]的坐标;

（3）在（2）的条件下，求[△A1B1C1]在旋转过程中扫过的面积.（结果保留[π].）

分析：结合图形平移和旋转的意义作出图形，并求出扫过的圆心角为直角的扇形面积.

解：（1）如图6，△[A1B1C1]即为所求，点[A1]的坐标为[A10，2];

（2）如图6，[△A2B2C1]即为所求，点[A2]的坐标为[A2-3，-3];

（3）如圖6，因为[BC=42+42=42]，

所以[△A1B1C1]在旋转过程中扫过的面积为[90π×422360+12×3×4=8π+6.]

【评析】此题第（1）小题考查了平移作图的一般方法，即找出图形中的关键点，过关键点作直线，这条直线要与已知线段平行，在平行线上截取平移距离的长度，得到对应点，连接所有对应点即可得到平移后的图形;第（2）小题的作法同例2;第（3）小题考查了扇形面积和图形旋转之间的关系.

《标准》指出，在“图形的变化”部分要能够画出轴对称、旋转和平移后的图形. 通过掌握这些基本作图方法，有利于使学生从图形运动变化的角度看全等三角形、平行四边形、圆等几何图形，由静态几何转化为动态几何，更加了解图形的本质和意义.

2. 重视方法，借助尺规作图法，提升逻辑推理能力

尺规作图是帮助学生理解“图形的变化”的基础步骤. 一方面，作图为图形的变化提供了直观的图形条件;另一方面，作图也为运动提供了轨迹和思路. 同时，在作图的过程中，体现了图形的运动路径，有利于发现运动中的不变性，从而有效解决问题，最终达到提升学生逻辑推理核心素养的目的.

例4 （湖南·长沙卷）如图7，人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法.

已知：∠AOB.

求作：∠AOB的平分线.

作法：（1）以点O为圆心，适当长为半径画弧，交OA于点M，交OB于点N.

（2）分别以点M，N为圆心，大于MN的长为半径画弧，两弧在∠AOB的内部相交于点C.

（3）画射线OC，射线OC即为所求（如图7）.

试根据提供的材料完成下面问题.

（1）这种作已知角的平分线的方法的依据是_________.

（填序号）

① SSS  ② SAS  ③ AAS  ④ ASA

（2）试证明OC为∠AOB的平分线.

分析：（1）根据题意填写作图依据;（2）利用（1）的作图依据，借助三角形全等进行证明.

解：（1）①;

（2）由基本作图方法，得

OM = ON，OC = OC，MC = NC.

因为在△OMC和△ONC中，△OMC ≌ △ONC（SSS），

所以∠AOC = ∠BOC，即OC为∠AOB的平分线.

【评析】此题来源于教材，是对教材的“再理解”，其中蕴含着与轴对称相关联的知识点. 从教材或配套练习册中选取素材进行变式成为中考命题的一种角度. 因此，深度剖析教材、注重对教材中典型例题（练习题）资源的利用，也是促进问题解决的关键. 学生在掌握基础知识、基本技能的同时，通过基本活动经验和基本思想方法的体验，能让“数学化”学习过程自然发生，以此深化数学思考，明晰数学本质.

例5 （四川·达州卷）如图8，点[O]在[∠ABC]的边[BC]上，以[OB]为半径作[⊙O，∠ABC]的平分线[BM]交[⊙O]于点[D]，过点[D]作[DE⊥BA]于点[E.]

（1）尺规作图（不写作法，保留作图痕迹），补全图形;

（2）判断[⊙O]与[DE]交点的个数，并说明理由.

分析：（1）根据题意作出圆、角平分线和垂线;（2）根据切线的性质判断[⊙O]与[DE]的位置关系.

解：（1）补全后的图形如图9所示.

（2）直线[DE]与[⊙O]相切，交点只有一个.

理由：因为[OB=OD，]

所以[∠ODB=∠OBD.]

因为[BD]平分[∠ABC，]

所以[∠ABM=∠CBM.]

所以[∠ODB=∠ABD.]

所以[OD∥AB.]

因为[DE⊥BA，]

所以[DE⊥OD.]

所以直线[DE]是[⊙O]的切线.

所以[⊙O]与直线[DE]只有一个交点.

【评析】此题中的尺规作图法体现在：作圆，作角平分线，过直线外一点作已知直线的垂线. 凸显了综合作图与基本作图的关联，再根据轴对称和全等的相关性质，建立求作与已知之间的联系，从而找到解决问题的方法. 此题展现了动手与动脑的和谐，又融入了对相关几何知识的理解，是一种深层次的“做中学”.

例6 （浙江·舟山卷）如图10，在等腰三角形[ABC]中，[AB=AC=25，BC=8，] 按下列步骤作图：① 以点[A]为圆心，适当的长度为半径作弧，分别交[AB，AC]于点[E，F，] 再分别以点[E，F]为圆心，大于[12EF]的长为半径作弧相交于点[H，] 作射线[AH];

② 分别以点[A，B]为圆心，大于[12AB]的长为半径作弧相交于点[M，N，] 作直线[MN，] 交射线[AH]于点[O];

③ 以点[O]为圆心，线段[OA]长为半径作圆.

则[⊙O]的半径为（    ）.

（A）[25] （B）10

（C）4 （D）5

分析：如图11，设[OA]交[BC]于点[T.] 解直角三角形求出[AT]的长，再在[Rt△OCT]中利用勾股定理构建方程即可解决问题.

解：如图11，设[OA]交[BC]于点[T.]

因为[BC=8，AO]平分[∠BAC，]

所以[AO⊥BC]，[BT=TC=4.]

所以[AT=AC2-CT2=252-42=2.]

在[Rt△OCT]中，則有[r2=r-22+42.]

解得[r=5.]

故此题选[D.]

【评析】此题看似作图步骤复杂，但若从轴对称方向观察，其实就是轴对称性质的“集合”，利用轴对称性质构造基本图形——等腰三角形的三线合一. 此题除了可以运用勾股定理列方程求解，还可以利用三角函数求解，即利用[sin∠B=sin∠AON，] 直接计算OA的长度. 再次体现了利用基本作图法和基本图形分析法解决问题的思路，灵活性较强.

例7 （福建卷）如图12，C为线段AB外一点.

（1）求作四边形ABCD，使得CD∥AB，且CD = 2AB;（要求：尺规作图，不写作法，保留作图痕迹.）

（2）在（1）的四边形ABCD中，AC，BD相交于点P，AB，CD的中点分别为M，N，求证：M，P，N三点在同一条直线上.

分析：（1）借助基本作图法以平移运动，作[CD∥AB，] 再作[CD=2AB.]

（2）借助“X”型基本图形，证明△APM ∽ △CPN，得到∠CPN + ∠CPM = 180°，继而得到M，P，N三点共线.

解：（1）如图13，四边形ABCD即为所求.

（2）证明：如图14，因为CD∥AB，

所以∠ABP = ∠CDP，∠BAP = ∠DCP.

所以△ABP ∽ △CDP.

因为AB，CD的中点分别为M，N，

所以AB = 2AM，CD = 2CN.

连接MP，NP，

因为∠BAP = ∠DCP，

所以△APM ∽ △CPN.

所以∠APM = ∠CPN.

因为点P在AC上，

所以∠APM + ∠CPM = 180°.

所以∠CPN + ∠CPM = 180°.

所以M，P，N三点在同一条直线上.

【评析】此题第（1）小题内涵丰富，有三种方法可达成“过直线外一点作已知直线的平行线”. 在进行尺规作图时，有意识地启动一题多解，并对每种作图方法都给出逻辑证明，这样可以在历练学生基本作图能力的基础上，使其知法明理;第（2）小题中证明“三点共线”需要学生具备很强的论证能力，联系中心对称的相关性质，体现“基本作图法”和“基本图形分析法”的有机结合，通过融入思维直觉与逻辑推理，在动手动脑中培养学生的数学学科核心素养.

问题解决体现了“行动 + 反思”的学习过程：尺规作图既有具体的运动行为，也有对运动过程的表示及作图后的反思，即将“外部操作活动”转化为“内部思维活动”的问题载体. 充分利用《标准》中的基本作图法，通过作图将复杂问题简单化，体现了转化思想.

3. 重视应用，设置问题情境，加强综合分析能力

“图形的变化”部分的试题往往会和实际问题或函数问题相结合，通过设置具体的问题情境，体现思考、作图和证明的逻辑链，彰显数形结合思想. 这正是《标准》所提倡的“经历观察、实验、猜测、计算、推理、验证等活动过程”，考查了学生合情推理和演绎推理的能力.

例8 （上海卷）如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形.下列图形中，平移重合图形是（    ）.

（A）平行四边形 （B）等腰梯形

（C）正六边形 （D）圆

分析：根据“平移重合”的概念判断.

解：如图15，在[▱ABCD]中，取[BC，AD]的中点[E，][F，] 連接[EF.]

因为四边形[ABEF]向右平移可以与四边形[EFCD]重合，

所以[▱ABCD]是平移重合图形.

【评析】此题通过阅读理解的形式考查了图形平移的性质. 近年来，以阅读理解和图形的变化相结合的试题屡见不鲜. 由此可见，通过阅读挖掘试题本质才是关键.

例8 （新疆生产建设兵团卷）如图16，在平面直角坐标系中，点[O]为坐标原点，抛物线[y=ax2+bx+c]的顶点是[A1，3，] 将[OA]绕点[O]顺时针旋转[90°]后得到[OB，] 点[B]恰好在抛物线上，[OB]与抛物线的对称轴交于点[C.]

（1）求抛物线的解析式;

（2）[P]是线段[AC]上一动点，且不与点[A，C]重合，过点[P]作平行于[x]轴的直线，与[△OAB]的边分别交于[M，N]两点，将[△AMN]以直线[MN]为对称轴翻折，得到△[A′MN，] 设点[P]的纵坐标为[m.]

① 当△[A′MN]在[△OAB]内部时，求[m]的取值范围;

② 是否存在点[P，] 使[S△A′MN=56S△OA′B，] 若存在，求出满足条件[m]的值;若不存在，说明理由.

分析：（1）抛物线[y=ax2+bx+c]的顶点是[A1，3，]可以假设抛物线的解析式为[y=ax-12+3，] 通过旋转的意义，求出点[B]的坐标，利用待定系数法即可解决问题.（2）根据翻折的意义画出图形，① 根据△[A′MN]在[△OAB]内部，构建不等式即可解决问题;② 求出直线[OA，AB]的解析式，求出[MN，] 利用面积关系构建方程即可解决问题.

解：（1）因为抛物线[y=ax2+bx+c]的顶点为[A1，3]，

所以设抛物线的解析式为[y=ax-12+3.]

因为[OA]绕点[O]顺时针旋转[90°]后得到[OB.]

所以设点[B]的坐标为[B3，-1.]

把[B3，-1]代入[y=ax-12+3，] 得[a=-1.]

所以抛物线的解析式为[y=-x-12+3，]

即[y=-x2+2x+2].

（2）① 如图17，因为[B3，-1，]

所以直线[OB]的解析式为[y=-13x.]

因为[A1，3，]

所以[C1，-13.]

因为[P1，m，AP=PA′，]

所以[A′1，2m-3.]

由题意[-13<2m-3<3，] 得[43<m<3.]

② 因为直线[OA]的解析式为[y=3x]，直线[AB]的解析式为[y=-2x+5，P1，m，]

所以[Mm3，m，N5-m2，m.]

所以[MN=5-m2-m3=15-5m6.]

因为[S△A′MN=56S△OA′B，]

所以[12 · m-2m+3 · 15-5m6=56×12×2m-3+13×3.]

整理，得[m2-6m+9=6m-8.]

解得[m1=6+19]（舍），[m2=6-19.]

当点[P]在[x]轴下方时，同理，可得[m3=6-393，][m4=6+393]（舍）.

所以满足条件的[m]的值为[6-19]或[6-393.]

【评析】此题体现了在直角坐标系中解决“图形的变化”的问题，需要图形在坐标系中有“位置”，这个“位置”就是图形在直角坐标系中的坐标. 借助基本作图法，作出旋转、翻折后的图形，利用全等三角形的性质求出其坐标. 函数背景下的图形的变化问题，其本质是借助数形结合思想，理清变化前后图形之间的关系.

例9 （江苏·南京卷）如图18（1），要在一条笔直的路边[l]上建一个燃气站，向[l]同侧的[A，B]两个城镇分别铺设管道输送燃气.试确定燃气站的位置，使铺设管道的路线最短.

（1）如图18（2），作出点[A]关于[l]的对称点[A，] 线段[AB]与直线[l]的交点[C]的位置即为所求，即在点[C]处建燃气站，所得路线[ACB]是最短的.

为了证明点[C]的位置即为所求，不妨在直线[l]上另外任取一点[C，] 连接[AC，BC，] 证明[AC+CB<][AC′+C′B.] 试完成这个证明.

（2）如果在[A，B]两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域. 试分别给出下列两种情形的铺设管道的方案（不需说明理由）.

① 生态保护区是正方形区域，位置如图18（3）所示;

② 生态保护区是圆形区域，位置如图18（4）所示.

分析：（1）借助轴对称的性质作出图形;（2）借助轴对称、正方形和圆的切线性质作出最短路线.

解：（1）如图19，连接[A′C′，]

因为点[A，A′]关于直线[l]对称，点[C]在[l]上，

所以[CA=CA′.]

所以[AC+BC=A′C+BC=A′B.]

同理，可得[AC′+C′B=A′C′+BC′.]

因为[A′B<A′C′+C′B，]

所以[AC+BC<AC′+C′B.]

（2）如图20，在点[C]处建燃气站，铺设管道的最短路线是折线[ACDB]（其中点[D]是正方形的顶点）;如图21，在点[C]处建燃气站，铺设管道的最短路线是折线[ACD，][DE，EB]构成的曲线（其中[CD]，[BE]都与圆相切）.

【评析】此题是“将军饮马”问题的典型变式. 第（1）小题利用轴对称的相关性质证明了最短距離问题，建立了数学模型;第（2）小题借助第（1）小题的模型，解决了正方形和圆背景下的最短路径问题，考查了学生数学抽象和数学建模的核心能力.

“图形的变化”虽然可以与不同背景的问题相结合，但是其作图依据还是来源于图形变换的性质. 熟悉各种类型的作图方法，了解各类作图的原理，才能在“图形的变化”的新情境中游刃有余.

三、复习建议

通过对2020年全国部分地区中考数学试卷中“图形的变化”部分试题的分析，笔者认为在中考复习中应该注意以下三点.

1. 认识几何作图的价值，为“图形的变化”的教学奠定基础

画图意识的培养不是一蹴而就的，教学中应设计适当的问题（任务），引导学生画图、用图，除了培养学生基本的画图技巧，还要加强学生的图形语言表达能力.

在“图形的变化”的教学中，教师要紧密联系学生熟悉的实例，使学生认识生活中的图形变换，以观察、动手操作为主要方式组织学生开展实践活动，切实把握好图形变换的具体目标及其要求的“度”. 例如，利用“图形的变化”设计图案是一项十分有趣的实践活动，教师应该充分发挥学生的主动性和创造性，引导学生自主设计漂亮的图案，在这样的活动中，学生主动进行基本作图技能的训练，这能对培养学生的类比推理及演绎推理能力起到潜移默化的作用.

2. 加强教学活动设计，为活动经验和数学思想方法的积累搭建平台

“图形的变化”的教学不能仅停留在“作图”这个层面，要通过归纳等手段，引导学生理解作图的依据，发现变化中的不变性. 只有深谙几何知识原理，才能驾轻就熟地解决这类问题. 当然，“图形的变化”的问题背景千变万化，这就要求我们在日常教学时贯穿“能作图时尽量作图”，在作图的基础上看图说话、用图探究. 同时紧扣“四基”，回归到数学知识的层面去分析和解释问题，并注重日常积累，这样才有利于培养学生的综合能力.

3. 以作图为抓手，在“图形的变化”的应用中提升数学素养

“图形的变化”的应用不仅局限于作图或几何证明，而更多地体现在生活中的应用. 例如，将图形的变化与图形设计相结合，将实际生活中的问题抽象成数学问题等，有助于培养学生的数学建模素养.

通过解决此类问题，可以使学生透过运动的过程看本质，在复杂图形中发现基本图形，体验数学在解决实际问题中的价值和作用，有利于激发学生的数学学习兴趣，培养学生的创新意识和实践能力.

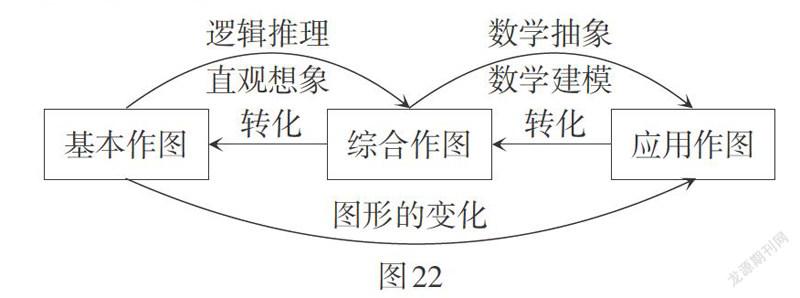
如图22，体现了以作图为抓手的“图形的变化”的学习进程，无论是应用作图还是综合作图，最终都落实为基本作图，体现了扎实基础、回归本源的重要性. 而每上升一个层级，又促进了学生数学学科核心素养的提升. 由此可见，以作图为基点，积累“图形的变化”相关问题的解题经验，是培养学生几何直观、发展学生空间观念、提高学生发现问题和解决问题的能力的助力器.

参考文献：

[1]中华人民共和国教育部制定. 义务教学数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]仇恒光. 尺规作图教学的策略探究[J]. 中学数学教学参考（中旬），2018（4）：61-63.

[3]李铁安. 义务教育课程标准（2011年版）案例式解读（初中数学）[M]. 北京：教育科学出版社，2012.