氯盐环境下钢筋锈蚀损伤混凝土应力应变本构模型

钟小平, 戴仁礼, 袁承斌, 夏 晋, 彭蓝鸽

(1.扬州大学 建筑科学与工程学院, 江苏 扬州 225127; 2.扬州大学 水利科学与工程学院, 江苏 扬州 225009; 3.浙江大学 结构工程研究所, 浙江 杭州 310058)

对于氯盐环境下的钢筋混凝土结构,氯盐侵蚀及由此引起的钢筋锈蚀膨胀力都将使混凝土产生损伤[1-3].混凝土受到损伤后,其应力-应变本构关系将发生改变,而钢筋锈蚀损伤混凝土应力-应变本构关系是研究服役钢筋混凝土结构剩余承载力和变形性能的基础,也是服役结构非线性有限元分析时必不可少的本构关系.

然而,目前有关氯盐环境下钢筋锈蚀损伤混凝土应力-应变本构关系的研究还很少.先前的研究主要关注了不同环境条件下(温度、湿度、干湿交替等)氯盐单因素作用对混凝土的侵蚀特性[4-5]、损伤机理[6-7]、抗压强度[8]、抗折强度[9]、动力学特性[10-11]及变形性能[12]等方面.研究表明,氯盐腐蚀初期对混凝土抗压强度有一定益处,但后期抗压强度、抗折强度、动力学特性等均有明显降低.这些研究成果为深入分析氯盐腐蚀混凝土的损伤机理及力学性能退化规律提供了理论基础.然而,实际氯盐环境中的混凝土结构损伤尤其是钢筋混凝土梁、柱等的损伤,除了氯盐腐蚀造成的损伤以外,由氯盐侵蚀引起的钢筋锈蚀膨胀力作用于混凝土,也会导致混凝土产生开裂、剥落等损伤[13-14],即混凝土损伤是氯盐腐蚀及由此引起的钢筋锈蚀膨胀损伤共同作用的结果,仅考虑氯盐腐蚀损伤部分不能真实反映混凝土力学性能的退化规律.鉴于此,本文通过实验室加速腐蚀试验,对氯盐环境下钢筋锈蚀损伤混凝土的力学性能进行试验研究,建立氯盐环境下钢筋锈蚀损伤混凝土应力-应变本构模型,以期为服役钢筋混凝土结构抗力退化及结构非线性有限元分析提供准确的材料性能参数.

1 试验

1.1 原材料及试件设计

水泥采用42.5级普通硅酸盐水泥;粗骨料采用粒径为5～20mm连续级配的碎石;细骨料为天然河砂,细度模数为2.49;水为普通自来水.混凝土配合比见表1.

表1 混凝土配合比

采用150mm×150mm×300mm的棱柱体试件.根据钢筋混凝土构件的布筋特点,在试件的4个角上内置直径为16mm、长度为240mm的HRB400级钢筋,如图1所示.钢筋锈蚀对混凝土试件造成的损伤程度以钢筋锈蚀率来表征,设计钢筋理论锈蚀率ρ为0%(未锈蚀,对照组)、3%、6%、9%,每组制作6个试件,其中3个用于测定混凝土的轴心抗压强度和应力-应变全曲线(A组),另外3个用于测定混凝土的弹性模量(B组).浇筑试件之前,在钢筋末端接上导线,用于对试件进行通电加速腐蚀试验.试件浇筑成型24h后拆模,在(20±2)℃和相对湿度95%以上的标准养护室中养护至28d,之后进行加速腐蚀试验.

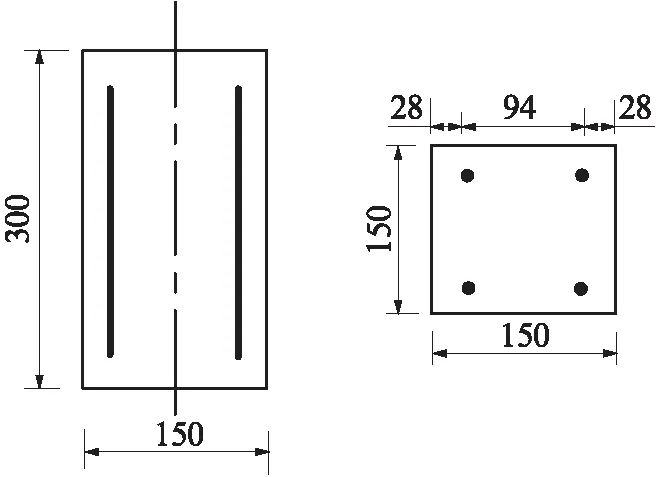
图1 钢筋布置示意图Fig.1 Schematic diagram of steel bar arrangement(size：mm)

1.2 加速腐蚀试验

将试件放置于质量分数为5%的氯化钠溶液中进行“恒电流-氯盐干湿循环”加速腐蚀试验.干湿循环周期采用14d,干湿循环比例为1∶1,即干7d湿7d,干燥时室内平均气温15℃,平均相对湿度70%左右.加速锈蚀过程中将稳压直流电源的负极连接于包裹在试件表面的不锈钢丝网上,待锈蚀钢筋与电源的正极连接,湿态时通电开始,干态时通电停止.腐蚀电流密度采用i=0.2mA/cm2,锈蚀钢筋表面积选取所有待锈蚀钢筋表面积之和,计算得到每个试件所需的通电电流大小I=0.11A.根据设计的钢筋理论锈蚀率ρ,采用Faraday腐蚀定律计算得到预期的通电时间t、干湿循环时间tw及干湿循环次数N,结果见表2.分别达到各自的通电时间后,加速腐蚀试验结束.

表2 钢筋锈蚀损伤混凝土试件加速腐蚀参数计算结果

1.3 加载试验及钢筋锈蚀率测定

钢筋锈蚀损伤混凝土应力-应变全曲线及弹性模量测试在YAW-G3000kN微机控制电液伺服高刚度岩石混凝土试验机上进行.试件上、下端安装激光位移计,采用等变形加载.应力-应变全曲线测试时,上升段以0.2mm/min的速率加载,达到峰值应力后,下降段以0.15mm/min的速率进行卸载,直至曲线逐渐平稳试验结束;弹性模量测试时,弹性阶段以0.15mm/min的速率加载至变形为0.3mm,然后以同样的速率卸载至变形为0.1mm,如此进行3次加载,在最后一次加载完成后,以0.2mm/min 的速率加载至峰值,达到峰值应力后,下降段以0.15mm/min的速率进行卸载,直至曲线逐渐平稳试验结束.试件荷载及总变形等数据由计算机自动采集并记录.

应力-应变全曲线及弹性模量测试完成后,取出锈蚀钢筋,除锈、烘干处理后,测定钢筋锈蚀后质量,然后采用失重法计算获得全曲线组试件(A组)和弹性模量组试件(B组)的实测平均锈蚀率ρc,结果如表3所示.

表3 钢筋实测平均锈蚀率统计表

2 结果与分析

2.1 钢筋锈蚀损伤混凝土试件外观

氯离子侵入混凝土内部,在使混凝土遭到腐蚀的同时引发钢筋锈蚀,当钢筋锈蚀膨胀力超过混凝土抗拉强度后,混凝土被胀裂.观察损伤试件表观状况(如图2所示)发现,沿钢筋长度方向,试件表面均出现了不同程度的顺筋锈胀裂缝,并且随着钢筋锈蚀率的增加,锈胀裂缝逐渐贯通,裂缝宽度逐渐增大,裂缝处有锈蚀产物溢出.

图2 损伤试件表观状况Fig.2 Surface conditions of damaged specimens

2.2 破坏过程与形态

观察未锈蚀和锈蚀损伤混凝土试件的加载过程,发现二者的破坏过程与破坏形态并不完全相同.未锈蚀损伤试件加载初期应力-应变按一定比例增长,随着荷载的增大,试件逐渐进入弹塑性阶段,当接近峰值应力时,试件中部出现少量竖向细微裂缝,达到峰值应力后,承载力缓慢下降,试件出现多条不连续的竖向裂缝,裂缝尖端逐渐贯通形成斜向破裂面.

对于锈蚀损伤混凝土试件,由于加载前已经受到损伤,存在与受力方向大致平行的锈胀裂缝,因此,从开始加载到试件破坏的整个受力过程中,锈胀裂缝宽度逐渐增大,应变增长较快.临近峰值荷载时,棱柱体试件中部相继出现了竖向细微加载裂缝,并向试件两端发展,试件端部的混凝土开始剥落.达到峰值应力后,锈胀裂缝和试件中部的加载裂缝宽度发展迅速,横向变形加剧,棱柱体沿锈胀裂缝和加载裂缝被劈裂成几个小柱体,这些微小柱体继续失稳破坏,棱柱体的承载力逐渐降低,核心混凝土被压坏,最后形成以锈胀裂缝为主的破裂面.

2.3 应力-应变全曲线

2.3.1实测应力-应变全曲线

将实测荷载和纵向位移分别换算为应力σc和应变εc,得到不同钢筋锈蚀率试件的应力-应变全曲线(见图3),每条曲线均取自3个试件的平均值.由图3可见：不同钢筋锈蚀率试件应力-应变全曲线形状及特征大体相同,均由上升段和下降段组成;在应力-应变全曲线上升段,随着钢筋锈蚀率的增加,应力-应变曲线的斜率逐渐减小,峰值应变增大,峰值应力降低,说明锈蚀损伤对混凝土的强度和变形均产生了一定的影响;当应力超过峰值应力后,曲线进入下降段,不同钢筋锈蚀率试件的强度并不完全消失,随着应力的减小(卸载),应变仍然增加.

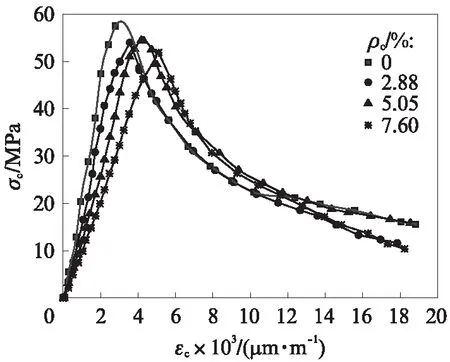
图3 不同钢筋锈蚀率试件的应力-应变全曲线Fig.3 Stress-strain curves of specimens with different corrosion ratios

2.3.2力学性能指标

表4给出了各混凝土试件的峰值应力σ0,c、峰值应变ε0,c和极限应变εcu,c.其中,极限应变εcu,c取钢筋锈蚀损伤混凝土应力-应变全曲线下降段0.85倍峰值应力处对应的应变值[15-16].

表4 各混凝土试件的峰值应力、峰值应变和极限应变

由表4可见,钢筋锈蚀损伤混凝土的峰值应力σ0,c均低于未锈蚀损伤试件,当钢筋实测平均锈蚀率ρc从0增加到2.88%时,峰值应力σ0,c降低速率较快,较未锈蚀损伤试件降低了6.1%;随着ρc的增加,σ0,c降低速率减小,当ρc达到7.60%时,钢筋锈蚀损伤混凝土的峰值应力σ0,c较未锈蚀损伤试件降低了9.8%.分析原因：钢筋锈蚀作用初期,锈蚀膨胀力使混凝土内部产生了微裂缝,并已发展到试件表面形成了可见的锈胀裂缝,见图2(b),试件由里及表受到损伤,外围胀裂部分混凝土对核心混凝土的横向约束能力快速减弱,其受力状态基本上相当于核心区域混凝土的受力状态,因而峰值应力降低较快;随着腐蚀时间延长,ρc增加,抗压强度主要由核心混凝土提供,由于锈胀力尚未使面积较大的核心混凝土胀裂,锈蚀对核心混凝土强度降低的影响减小,因而峰值应力降低速率减小.由表4还可以看出,试件峰值应变和极限应变随着ρc的增加,基本呈线性增长.当ρc达到7.60%时,试件峰值应变和极限应变较未锈蚀损伤试件分别增长了81.7%和64.6%.可见,钢筋锈蚀损伤对试件峰值应力、峰值应变、极限应变均有较大的影响.通过对表4中试验数据进行拟合,得到了峰值应力、峰值应变、极限应变与实测平均锈蚀率之间的关系：

σ0,c=57.047-0.6708ρc,ρc≤7.6%

(1)

ε0,c=0.0028+0.0003ρc,ρc≤7.6%

(2)

εcu,c=0.0037+0.0003ρc,ρc≤7.6%

(3)

式(1)～(3)的拟合相关系数分别为0.8684、0.9937、0.9756,可见拟合结果较好.

2.3.3应力-应变全曲线方程

对实测的应力-应变全曲线进行无量纲化处理,横坐标采用εc/ε0,c表示,纵坐标采用σc/σ0,c表示,如图4所示.

图4 本构模型与实测曲线对比Fig.4 Comparison of constitutive models with experimental curves

由图4可见,实测曲线的上升段和下降段有明显的区别,上升段各曲线基本重合,近似线性发展;达到峰值应力后,随钢筋实测平均锈蚀率增加,曲线下降段坡度变陡,说明钢筋实测平均锈蚀率越大,试件脆性越明显.根据曲线上升段和下降段各自的特点,分别选用不同的函数,采用最小二乘法拟合试验结果，得到应力-应变全曲线本构模型.

上升段[17]:

y=ax+(3-2a)x2+(a-2)x3, 0≤x≤1

(4)

下降段:

y=bxβ,x>1

(5)

式中:y=σc/σ0,c;x=εc/ε0,c;a为曲线上升段控制参数;b、β为曲线下降段控制参数.

通过拟合分析,得到曲线上升段和下降段控制参数a、b和β随ρc变化的表达式：

a=0.0035ρc2-0.017ρc+0.641

(6)

b=-0.0043ρc2+0.0271ρc+1.0297

(7)

β=-0.0043ρc2-0.026ρc-0.7182

(8)

为了验证本文给出的应力-应变全曲线本构模型的适用性,图4给出了本构模型与实测曲线的比较.由图4可见,应力-应变全曲线本构模型计算结果与实测结果吻合较好,将此模型应用于分析服役结构剩余承载力、变形性能以及非线性有限元模拟是可行的.

2.4 弹性模量

采用反复加载、卸载的方式对不同钢筋锈蚀损伤混凝土弹性模量进行测试,结果如图5所示.

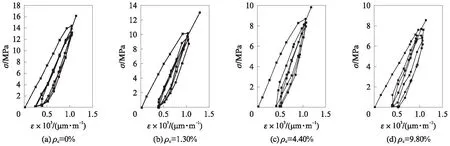
图5 钢筋锈蚀损伤混凝土弹性模量测试结果Fig.5 Elastic modulus test results of concretes damaged by rebar corrosion

由图5可见,由于钢筋锈蚀损伤混凝土的非弹性性质,每次卸载至零时,变形不能完全恢复,存在残余应变,且随着钢筋实测平均锈蚀率的增加,残余应变增大.当荷载重复3次后,不同锈蚀损伤混凝土的应变基本趋于稳定,应力-应变曲线接近于直线.取最后一次加载的应力-应变全曲线上应力σ=0.4σ0,c处割线的斜率作为混凝土弹性模量的取值[18],得到锈蚀损伤混凝土弹性模量Ec,c与钢筋实测平均锈蚀率的关系：

Ec,c=21.604-1.3364ρc,ρc≤10%

(9)

式(9)的拟合相关系数R2=0.9033,拟合结果较好,用其预测氯盐环境下钢筋锈蚀损伤混凝土的弹性模量是可行的.

3 结论

(1)钢筋锈蚀损伤混凝土试件的破坏多为微柱失稳破坏,大致平行于受力方向的锈胀裂缝是主要的破裂面.

(2)钢筋锈蚀损伤混凝土实测应力-应变曲线与未锈蚀损伤混凝土相似.但是,随着钢筋锈蚀率的增加,应力-应变全曲线上升段的斜率逐渐减小,峰值应变增大.当曲线进入下降段后,钢筋锈蚀率越大的试件,曲线下降段坡度相对越陡,脆性越明显.

(3)钢筋锈蚀损伤试件的峰值应力均低于未锈蚀损伤试件,峰值应变、极限应变随着钢筋锈蚀率的增加而增大,弹性模量随着钢筋锈蚀率的增加而减小.

(4)所建立的钢筋锈蚀损伤混凝土应力-应变本构模型计算值与实测值吻合较好,可为氯盐环境下服役钢筋混凝土结构承载力、变形性能以及非线性有限元分析提供理论依据.