基于有限元法摆线针轮温度场研究

宋雪萍，卢博文，毕爱宾

（大连交通大学机械工程学院，辽宁大连116028）

摆线针轮减速器具有刚度高、抗疲劳、寿命长、传动精度和回差精度稳定等优点，广泛应用于工业机器人关节部位，受到国内外企业的广泛关注。减速器整体性能和传动系统精度对工业机器人在高端制造业的影响不容忽视［1］。由于摆线针轮减速器结构紧凑且传动过程中会产生摩擦热，造成零部件热变形或在啮合处发生热胶合，从而对摆线针轮减速器的整体传动精度产生影响。因此，对摆线针轮传动系统进行温度场以及相关因素的分析是十分必要的，这对控制摆线针轮减速器的润滑与冷却以及提高其工作性能同样具有非常重要的参考意义［2］。本文根据摆线轮啮合原理，计算其运转过程中摩擦热，并对影响摩擦热的各因素进行了分析研究。在理论分析计算的基础上通过有限元分析，得到其实际运转过程中的稳态温度场，可直观地观察到啮合过程中温度过高区域，对摆线轮的润滑以及提高摆线针轮减速器回转精度提供依据。

1 摆线针轮传动系统热源分析

摆线针轮传动系统中的热源主要包括摆线针轮啮合摩擦热和轴承摩擦热［3］。

1.1 摆线针轮啮合摩擦热计算

1.1.1 摆线针轮啮合摩擦热流量

摆线轮轮齿与针轮轮齿在接触点处有摩擦而产生热量。由摆线轮与针轮啮合传动原理可知，摆线轮会以摆线轮齿由啮合到下一次啮合为周期运转，运转过程中所产生的啮合摩擦热量同样会呈现周期性。摆线轮运转一个周期接触区域为轮齿的一半，如图1所示，啮合位置为AB区域，可由啮合相位角φ决定。摆线齿与针齿在不同啮合位置的齿面摩擦热流量［2］为

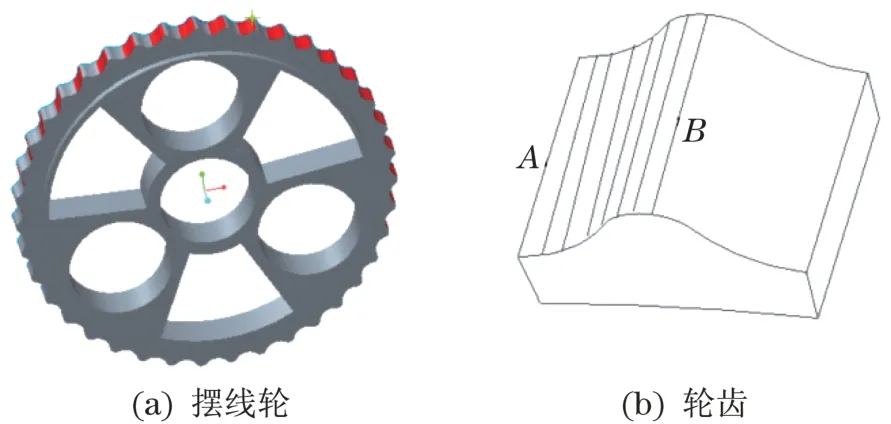
图1 齿面啮合区域Fig.1 Tooth surface meshing area

式中：σp为摆线齿与针齿间的齿面平均接触应力［2，6］；Vr为摆线齿与针齿间的相对滑动速度［7-8］；f为摆线齿与针齿间的摩擦系数［2，5］；γ为能量转换效率，即摩擦能转化为热能的转换系数，本文取0.9［2］。

根据齿面接触应力σp、摆线齿与针齿间的相对滑动速度Vr计算公式，联立得出相对于啮合相位角热流量q，q=q(φ，T)，根据表1相关参数，得出平均接触应力如图2所示，热流量如图3所示。

表1 模型主要参数Tab.1 Main par ameters of the model

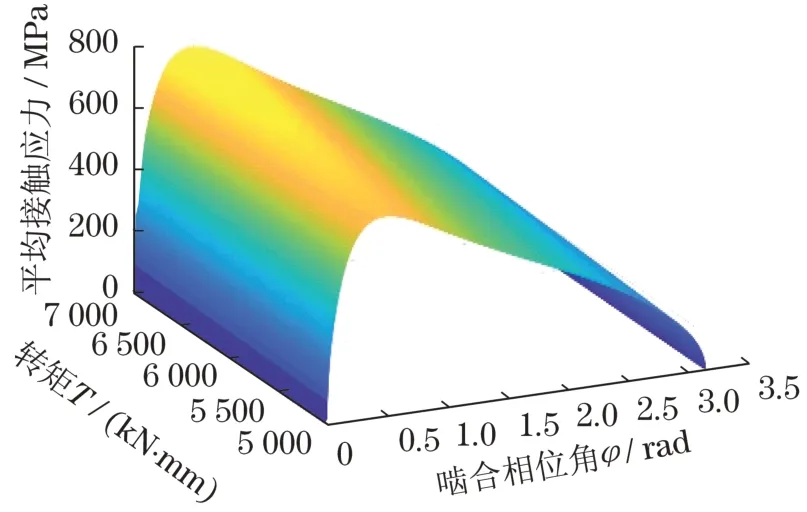
图2 平均接触应力分布Fig.2 Average contact stress distribution

图3 齿面热流量分布Fig.3 Heat flux distribution on the tooth surface

由图2可知，齿面热流量随着输出转矩的增加而增大，大致成正比例关系。在转矩确定情况下，热流量随着啮合相位角即啮合位置而改变。与平均接触应力分布图3比较可得，热流量最大值与接触应力最大值均在φ=0.5附近啮合位置，且分布趋势也较为接近。由此可得，热流量受接触应力影响较大。

1.1.2 摆线针轮啮合摩擦热量计算

摆线针轮摩擦热量公式为

式中；q为齿面摩擦热流量，W/m2；S为齿面啮合面，m2。

以摆线轮的几何中心为原点，建立坐标系，可得摆线轮齿廓的标准齿形方程式为［9］

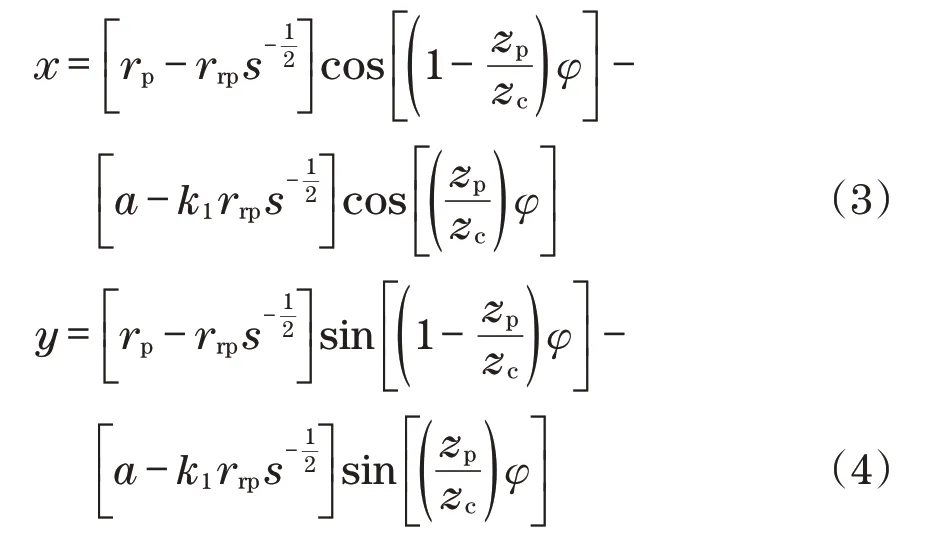
根据齿形方程可得啮合区域AB摆线弧长l基于啮合相位角φ函数为

根据式（1）、式（4），可得q和l都是基于啮合相位角φ的函数，通过代数换算可得热流量相对于弧长l的函数q(l)，则啮合区域总发热量Q为

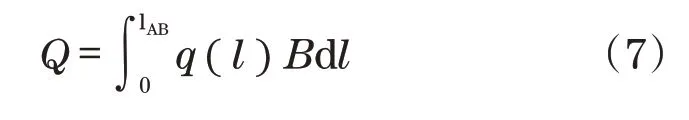
1.2 轴承摩擦热

摆线针轮传动系统中主要有主轴承（角接触轴承）、摆线轮支撑轴承（圆柱滚子轴承）以及偏心轴定位轴承（圆锥滚子轴承），其中摆线轮支撑轴承对摆线针轮啮合影响相对较大，所以，此处只计算支撑轴承热流量。滚动轴承的发热量主要来自于轴承滚子与滚道等摩擦副的摩擦生热。目前，计算轴承发热量的模型有很多，例如，Palmgren发热量计算模型、Astridge发热量计算模型、B.M.捷米道维奇发热量计算模型等。Palmgren发热量计算模型具有准确、简单、易算等优点，在工程计算中被广泛应用［10］。

Palmgren发热量计算模型轴承总的发热量H为

式中：H为轴承正常运行过程中的总发热量，W；M为总摩擦力矩，N·m；n为轴承内圈转速，r/min。

总摩擦力矩M为

式中：M为滚动轴承的总摩擦力矩，N·mm；Ml为轴承承载引起的摩擦力矩，N·mm；Mv为与轴承类型、转速和润滑油性质有关的摩擦力矩，N·mm；Ma为圆柱滚子轴承附加摩擦力矩，N·mm。

摆线轮支撑轴承载荷摩擦力矩Ml为

摆线轮支撑轴承润滑剂产生的黏性摩擦力矩Mv为

摆线轮支撑轴承圆柱滚子轴承附加摩擦力矩Ma为

式中：dm为轴承节圆半径；Fr为轴承所承受的径向载荷；Fa为轴承所承受的横向载荷。

根据摆线轮支撑轴承的受力情况可得［11］

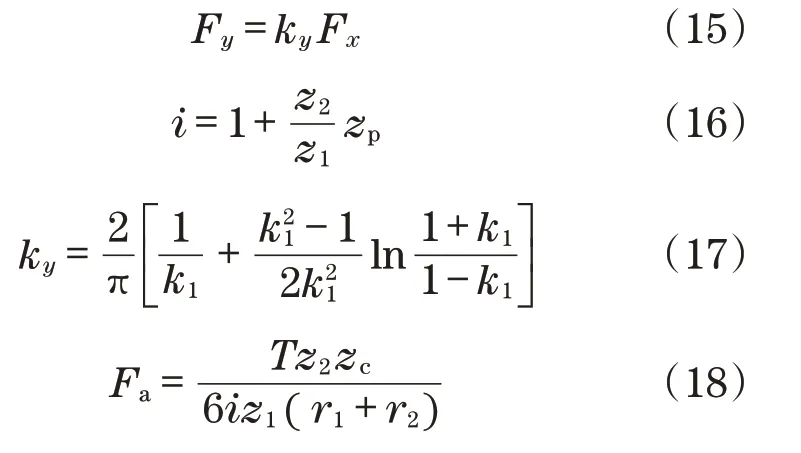
式中：i为减速器传动比；z1为中心轮齿数；z2为行星轮齿数；r1为中心轮半径；r2为行星轮半径。

根据摆线轮传动特性可知曲柄轴与输入轴的传动比为

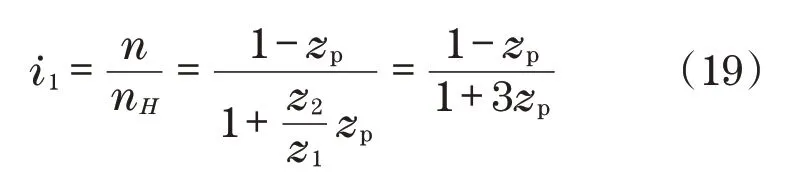
联立式（8）～式（19），推导计算可得摆线轮支撑轴承的发热量H，主要与输入轴转速nH以及输出转矩T有关，且其随输入轴转速nH以及输出转矩T变化曲线如图4所示。由图4可示，发热量与输入轴转速nH以及输出转矩T大致成正比例关系。

图4 发热量基于转矩与转速的变化曲线Fig.4 The heating value is based on the variation curve of torque and speed

1.3 对流换热系数

摆线针轮啮合传动过程中，摆线轮表面不同部分的对流换热系数是不同的，主要分为摆线轮轮齿齿面与润滑油对流换热和摆线轮端面与空气进行对流换热。且润滑油及空气性能如表2所示。

表2 润滑油及空气性能参数Tab.2 Performance parameters of lubricating oil and air

齿面对流换热系数公式［12］为

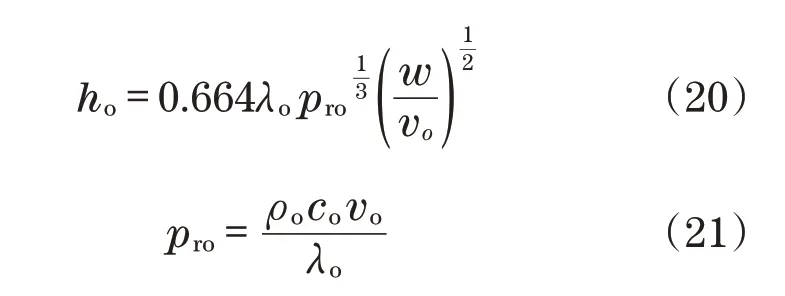
式中：λo为润滑油导热率；pro为普朗特数；w为摆线轮自转的角速度；vo为润滑油运动黏度；co为润滑油比热容；ρo为润滑油密度。

端面对流换热系数公式［13，24-26］：

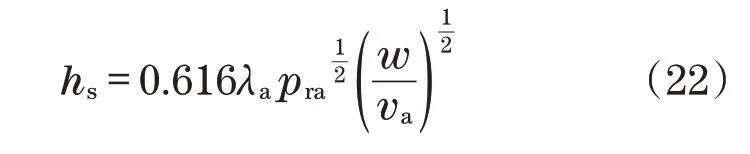
式中：λa为空气导热率；pra为普朗特数；w为摆线轮自转的角速度；va为空气运动黏度；ca为空气比热容；ρa为空气密度。

2 摆线轮有限元分析

在摆线针轮啮合区域以及轴承装载孔加载热量并分别在端面以及啮合面添加对流［14-15］。设置外界温度22℃、T=6 000 k N·mm和nH=1 500 r/min，以对模型进行求解得出温度分布云图，如图5所示。

图5 T=6 000 k N·mm摆线针轮温度分布云图Fig.5 T=6 000 k N·mm，the temperature distribution cloud diagram of the cycloid pin wheel

由图5可知：摆线轮啮合区域为高温区，由于单侧啮合，摆线轮齿面从接触区域一侧到非接触区域，温度逐渐降低，形成了鲜明的温度梯度；针齿运转过程中，发生自转，啮合区域为整个针齿圆柱面，所以温度梯度无明显变化。这说明由于温度分布的不均匀性，引起的冲击和振动，主要是由摆线轮齿面温差造成，在实际传动中需要进行充分考虑。

由图5可知，轴承摩擦热对摆线针轮影响可忽略不计，输入轴转速主要会对轴承热产生影响，所以输入轴转速对温度场影响的研究可忽略。控制单一变量，改变参数T=7 000 k N·mm对模型进行求解得出温度分布云图如图6所示。根据不同输出转矩下温度分布云图5以及图6可知，输出转矩对温度分布变化的趋势影响较小，温度场的最高温度由53℃变为63℃，与实际情况相符，随转矩增大而增大。

图6 T=7 000 k N·mm摆线针轮温度分布云图Fig 6 T=7 000 k N·mm，the temperature distribution cloud diagram of the cycloid pin wheel

考虑外界工作环境，设置外界温度为30℃和20℃，得到温度分布云图如图7和图8所示。根据不同外界温度下的温度云图5、图7与图8可知，外界温度对温度场的影响较大，外界温差会体现在温度场上。由此可知，摆线针齿啮合润滑要考虑到其工作环境温度以及减速器箱体的散热。

图7 T=6 000 k N·mm外界温度30℃摆线针轮温度分布云图Fig.7 T=6 000 k N·mm，ambient temperature 30℃，the temperature distribution cloud diagram of the cycloid pin wheel

图8 T=6 000 k N·mm外界温度20℃摆线针轮温度分布云图Fig.8 T=6 000 k N·mm，ambient temperature 20℃the temperature distribution cloud diagram of the cycloid pin wheel

3 结论

（1）摆线轮啮合摩擦热流量，随着输出转矩改变而改变，不同啮合线即不同啮合相位角处的热流量不同，其变化趋势与啮合齿面平均接触应力相似。

（2）摆线轮支撑轴（曲柄轴承）摩擦热量与输出转矩以及输入轴转速相关，且大致成正比例关系。

（3）由于温度分布不均匀性引起的冲击和振动，主要是由摆线轮齿面温差造成的，在实际传动中需要进行充分考虑。

（4）由摆线轮温度分布云图可得，摆线轮传动过程中，温度最高处为啮合区域，且轴承发热对摆线轮温度场的影响可忽略不计。不同转矩及不同外界温度下摆线轮温度场分布趋势变化较小，最高温度随转矩增大而增大。由外界温度温差会体现在温度场上可知，摆线针齿啮合润滑要考虑到其工作环境以及减速器箱体的散热。研究结果可为避免轮齿胶合、轮齿降温、轮齿修形等提供一定的理论基础。