某特大桥大体积混凝土温度控制理论分析
郭 静
(长治高速公路有限责任公司,山西长治 046000)
某特大桥大体积混凝土温度控制理论分析
郭静
(长治高速公路有限责任公司,山西长治046000)
摘要:结合某特大桥工程,以混凝土的力学性能、热学特性、热传导方程、热生成率、边值条件为基础,进行了绝热温升实验,研究了混凝土的最大温升值,并将实验值与理论计算值作了对比,指出两种结果基本相同,可通过理论计算进行混凝土的温度控制。
关键词:混凝土,绝热温升,导热系数,热流量
1 工程背景
某特大桥跨越某河流,当地地形为U型河谷,高差较大,且要跨越原高速公路,路线线位较高,桥墩高度平均超过60 m,桥梁全长1 534 m。上部结构采用4×40 m预应力混凝土先简支后连续T梁+45 m +75 m +45 m预应力混凝土刚构+30×40 m预应力混凝土先简支后连续T梁,下部结构采用薄壁矩形空心墩+承台+群桩基础,承台的平面尺寸为13.2 m×8.2 m,高度为3.5 m。
2 绝热温升实验
本实验利用绝热温升仪,测量在绝热的条件下,随着时间(测试时间为7 d)的变化,混凝土试件的中心温度发生的具体变化。试件的强度为C30(与该桥梁的设计强度一致),尺寸采用φ40× 40 cm,材料与配比均来源于该特大桥的工程现场。表1为混凝土材料的配合比。

表1 混凝土配合比 kg

图1 混凝土温升值曲线
由图1可知,初期时混凝土的放热速率呈上升趋势,之后逐渐放缓,最终温升值无限趋近于60℃。因此,温升曲线的方程可表示为:

其中,θ为绝热温升值; te为等效龄期,由式( 2)确定。

其中,Eh/R =2 400 K; T0=293.15 K。
3 热生成率的确定
热生成率Q可由温升曲线方程变形后得到,即为:

其中,θ为绝热温升。
4 热传导方程
如果假设某一个固体的各个方向性能相同,从其中取出一个极小的如图2所示的微元体dxdydz,那么,流入其的净热量为( qxqx + dx) dydz。
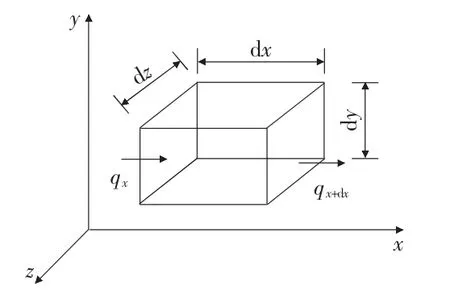
图2 微元体
在固体的传导中,流量q可表示为:

其中,λ为导热系数,kJ/( m·h·℃)。
式( 4)通过变化,得:

所以,沿x方向流入的净热量可表示为:

假设该微元体在时间长度为dτ的时间里,流入的热量可表示为
其中,c为比热;τ为时间;ρ为密度。
热量平衡方程为:

式( 8)通过变形后可得:

其中,a为导温系数。
经过变化,热传导方程可改写为:
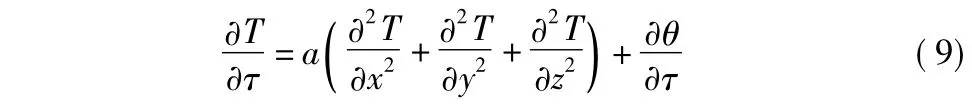
5 边值条件
6 混凝土的温度计算
6.1最大绝热温升

式中: mc——混凝土中水泥的用量;
F——混凝土中活性掺和料的用量;
K——掺和料折减系数,取0.25~0.3;
Q——水泥28 d水化热;具体值详见表2;
c——混凝土比热,取c =0.91 kJ/( kg· ℃) ;
ρ——混凝土密度,取ρ=2 400 kg/m3;
t——混凝土的龄期;
m——随浇筑温度而改变的系数,具体值详见表3;
Th——混凝土的最大绝热温升值。

表2 水泥水化热取值表

表3 随浇筑温度而改变的系数表
根据上式,得:

6.2混凝土中心计算温度

式中: Tp——混凝土的浇筑温度;
Th——混凝土最大绝热温升;
ξ( 1)——t龄期混凝土降温系数,在表4中取得;
T1( t)——混凝土t龄期的中心计算温度。

表4 不同龄期混凝土降温系数表
由上式得:

7 结语
由实验测得的混凝土的绝热温升值约为60℃,与理论计算的绝热温升值63.2℃基本相同,证明理论计算公式是具有参考性的。因此,在今后类似的工程施工过程中,我们可以通过理论计算,对实际的工程温度控制进行指导。
参考文献:
[1]李达,暴育红.大体积混凝土的温差裂缝控制措施及热工计算[J].混凝土,2006( 3) :88-90.
[2]苟季.大体积混凝土水化热对结构的影响研究[D].南宁:广西大学,2008.
[3]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.
[4]袁勇.混凝土结构早期裂缝控制[M].北京:科学出版社,2004:76-109.
[5]范奎.大体积混凝土水化温度场仿真计算与实测技术研究[D].杭州:浙江大学,2005.
On temperature control theory of large concrete at some super-large bridge
Guo Jing
( Changzhi Expressway Co.,Ltd,Changzhi 046000,China)
Abstract:Combining with some project at some super-large bridge,the paper undertakes the adiabatic temperature rising tests based on the dynamic performance,thermal characteristics,heat conduction equation,heat generation rate,and boundary conditions,researches the maximum temperature rising value of the concrete,compares the tested values with the theoretic ones,and points out the two results are basically similar,so the temperature control of the concrete can be operated by the theoretic calculation.
Key words:concrete,adiabatic temperature rising,heat conductivity coefficient,heat flux
作者简介:郭静(1988-),男,助理工程师
收稿日期:2015-11-22
文章编号:1009-6825( 2016) 04-0200-02
中图分类号:U445
文献标识码:A

