300 t履带起重机臂架应力分析与测试
孙岱华
(北京市特种设备检测中心,北京100029)
履带起重机的臂架是桁架臂类起重机的典型代表之一。目前此类中大吨位的起重机市场份额占有率较高,应用领域基本覆盖履带起重机涉及的所有领域,如市政工程建设、铁路公路交通建设、石油化工工程建设、海油工程建设、电力工程建设(包括火电风电核电)等[2]。故本文选取300 t履带起重机作为研究和试验对象。
履带起重机臂架结构体型庞大,非线性变形明显,通常臂架结构组合有3种:主臂组合、固定副臂组合和塔式副臂组合。具有超起装置的起重机还有超起主臂组合、超起固定副臂组合、以及超起、塔式副臂组合。无论主臂、固定副臂还是塔式副臂,它们的臂架结构组成相似,均是由底节、标准节、顶节组成,标准节随臂长的需求而增减对应的臂节数量,每节臂节都是由弦杆和腹杆组成桁架结构。从力学分析角度[3],三者的受力及应力分布规律趋于相近,主臂作为基础臂,截面大,承载能力强,因此起重量是三者中最大的,具有代表性。增设超起装置,改善臂架受力,但应力水平与标准型的接近,故本文对标准型主臂进行应力测试试验。
1 臂架有限元分析
本文通过ANSYS有限元模型的建立,以及对静力学的分析,确定臂架的应力水平及高应力区,为选取危险截面作为应力测试点提供理论依据。
根据臂架结构形式,采用梁单元Beam188模拟管状桁架结构,壳单元Shell63模拟臂架中的加强板结构,变幅拉板只承受拉力,采用杆单元Link8模拟。各连接铰耳中心建立质量点Mass21并与铰耳建立刚性区域连接,同时忽略对整体应力分布影响较小的构件[4]。
考虑到臂架实际作业时受力情况,臂架根部铰点除放开绕其自身销轴的约束外,其余自由度全约束,变幅拉板末端铰点进行全位移约束,变幅拉板顶端铰点与臂架头部连接点处施加耦合约束。加载时,在臂架头部起升滑轮耳板孔处按实际吊载施加节点载荷。由此建立的有限元模型如图1所示。
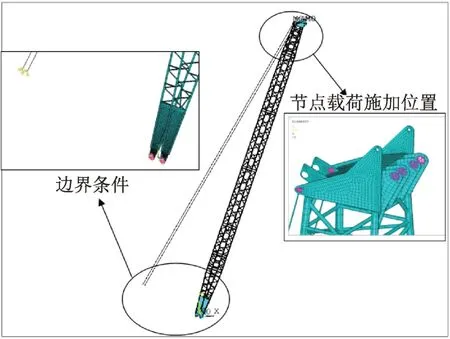
图1 臂架有限元模型Fig.1 FEM of boom
参照起重性能表,选取最短、中长、最长臂架对应的小幅度工况及起臂工况作为计算工况,如表1所示。根据规范[1,5],结合起重机实际作业情况确定起升动载系数为1.1,水平侧载荷为(tan 3°)Q(Q为起重量)。

表1 有限元载荷工况Tab.1 Load cases of the FEM for boom
考虑臂架几何特征,长臂时长细比较大,几何变形明显,因此,对比了线性计算和非线性计算的结果,工况6的应力分布与结果对比如图2和表2所示。可以看出,非线性应力要高于线性应力,按非线性计算结构应力是必要的。
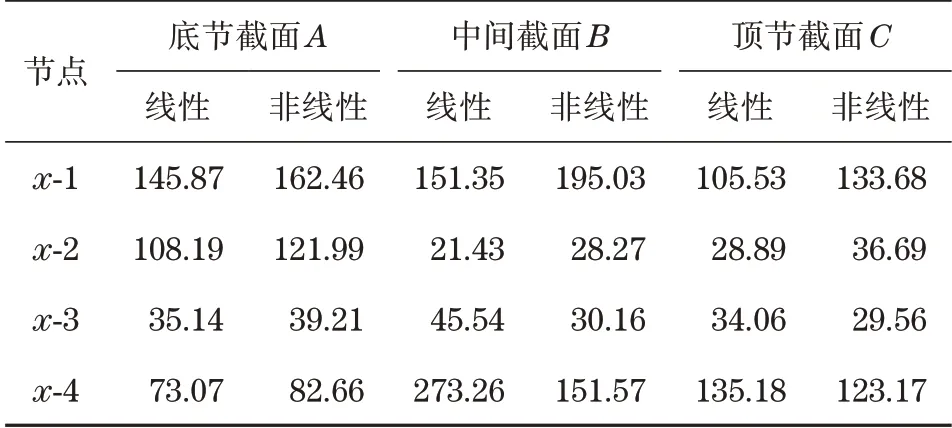
表2 线性与非线性有限元结果对比Tab.2 The comparison between linear and nonlinear results MPa

图2 线性与非线性有限元结果Fig.2 The results of linear and nonlinear FEM
表2中,x=1,2,3,4,如图3所示。
按非线性方法,计算表1的各工况,通过对计算数据结果的整理,可以确定臂架的危险截面有3处(见图3):①臂架底节与标准节连接附近的截面A,此处底节承受轴向载荷和侧向弯矩,而且截面小,导致应力较大;②臂架重心附近的截面B,此处承受臂架轴向载荷和一定的侧向弯矩,同时承受较大的自重分力引起的变幅平面内弯矩,使得此处的应力较大,臂架水平起臂时表现更为明显;③臂架顶节与标准节连接附近的截面C,此处截面变化,使得应力有一定的变化[6]。
汇总各工况危险截面有限元结果应力值如表3所示。
表3中可以看出:

表3 危险截面应力汇总表Tab.3 The stresses of dangerous sections MPa
(1)各工况应力水平相当,均在30~370 MPa范围内,与材料许用值501 MPa相比,材料利用率集中在50%左右。
(2)各工况应力分布趋势相近,不同工况下小幅度时的应力较大。同工况下,由于臂架承受轴向载荷和弯矩引起的弯曲应力,变截面处的应力较大。当有侧载时,臂架在回转平面内相当于悬臂结构,其根部的应力增大。
(3)水平起臂工况是臂架自拆装工艺中不可或缺的非作业环节,虽然不属于作业工况,但由于臂架水平放置,重心远离回转中心,使得臂架承受因自重引起的较大的弯曲应力,也是臂架的危险工况之一。其应力随臂长增加而增大,甚至与臂架作业工况的应力相当,因此,起臂工况在设计时要特别引起重视。
2 臂架应力测试试验
对工作状态下的300 t型履带起重机臂架进行应力测试,试验数据采集仪器及元件如表4所示。

表4 信号采集主要仪器设备与元件Tab.4 The main equipment and components for signal acquisition
为了充分了解作业过程中臂架应力分布,参考有限元计算结果,在危险区域A、B、C3个截面布置12个测点,A截面为底节靠近标准节第2个节点处;B截面为重心附近(臂架跨中)的2个节点中心处;C截面为顶节靠近标准节第1个节点处,各截面的测点位置和编号如图4所示。臂架弦杆在起升重物过程中主要受到轴向力的作用,以单向应力为主,主应力方向相对明确,将各截面的4个弦杆均沿轴向贴片,采用半桥的连接方式测试轴向应力[7],部分测点贴片如图5所示。
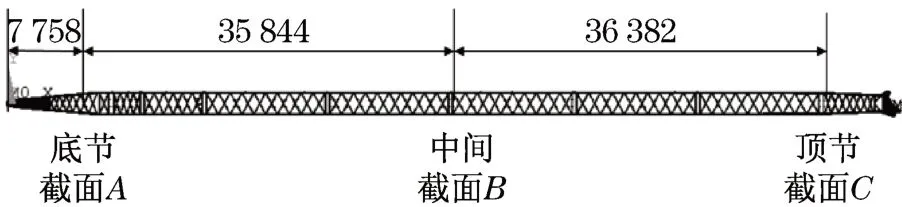
图4 臂架测试截面位置Fig.4 The test cross sections for boom

图5 贴片布置Fig.5 The layout of test points
通过理论分析和有限元计算,表明臂架在不同臂长下的应力水平相当,同臂长不同幅度下,小幅度应力值大于大幅度应力值。臂架起臂工况的应力水平随臂长增加而增加,与作业状态时的相当。因此考虑中长臂实际使用率高的特点,选取中长臂小幅度作为测试工况,如表5所示。

表5 试验工况Tab.5 The test cases
应力测试试验包括静态测试和动态测试。静态测试时砝码载荷平稳起升离地1 m后保持稳定,采集数据。动态测试包括臂架的起升、变幅、回转、卸载过程。臂架首先处于水平状态,如图6(a)所示;然后起臂,边回转边变幅到23 m幅度,如图6(b)所示。起升砝码,落下砝码,反复3次。记录各测点应力历程,如图7所示,其中,横坐标代表时间(s),纵坐标代表应力(MPa)。

图6 试验现场Fig.6 The test site
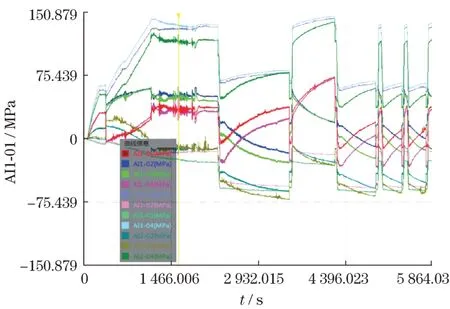
图7 测点应力时间历程示意Fig.7 The stress history of test points
试验过程中,发现测点2-1采集的数据飘移,可能测点贴片有误,因此,后续不再对此测点记录数据。从图7的试验记录数据变化曲线来看,对称布置的测点数据变化趋势相近,表明试验数据有效,具有参考价值。
3 结果对比分析
采集起重机保持平稳时的各测点数据记录,3次试验结果均值作为测试数据。由于初始状态应变片进行了清零设置,测试数据仅为砝码载荷引起的应力变化。因此,有限元计算时,将不考虑臂架和吊钩自重,按表5试验工况载荷施加在有限元模型上,计算出测点的轴向应力,并与静载试验结果对比(压为“-”,拉为“+”),如表6和表7所示。表中,误差率=(计算值-测试值)/测试值

表6 静载试验结果与有限元结果对比统计(工况SY1)Tab.6 The comparison of results between static test and FEA(SY1 case)

表7 静载试验结果与有限元结果对比统计(工况SY2)Tab.7 The comparison of results between static test and FEA(SY2 case)
由静态测试结果对比,可以看出:
(1)测点相对臂架纵向轴线对称布置,可以相互印证。左右对称布置的测点应力基本一致。上下对称布置的测点中,上平面测点x-1、x-4(x=1,2,3,4)的应力均大于下平面测点x-2和x-3(x=1,2,3,4),这是由于臂架处于作业状态时,上、下平面弦杆因存在自重分力引起的弯曲应力作用,使得上平面弦杆应力大于下平面弦杆应力。
(2)有限元计算结果与实车应力测试结果平均误差在13.8%左右,变化趋势相近,证明有限元模型的可靠性,可以预测臂架应力分布。
(3)个别测点误差达到20%,这可能是测点位置与有限元选取位置因网格划分情况存在一定偏差导致。
采集动态测试过程最大应力,并与静态测试结果对比,如表8和表9所示。表中,增幅=(动载应力-静载应力)/静载应力;误差率=(有限元应力-动载应力)/动载应力。
从表8和表9中可以看出:
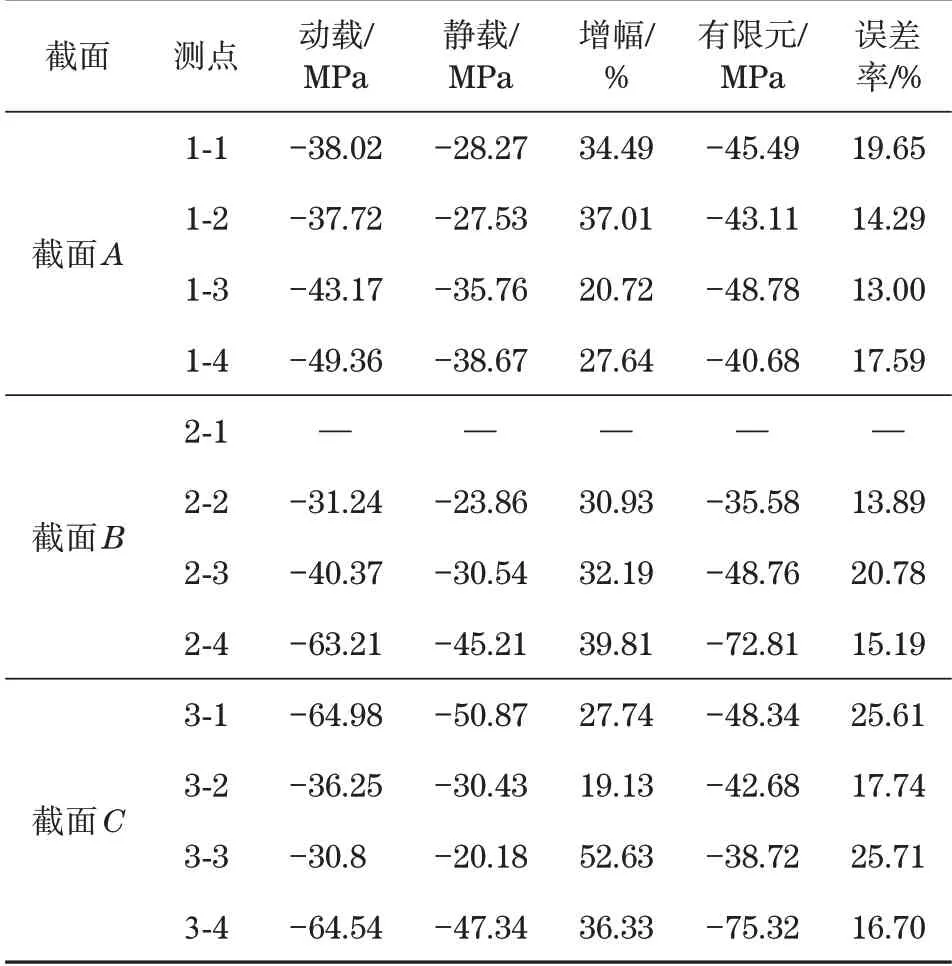
表8 动载试验结果与静载试验结果对比统计(工况SY1)Tab.8 The comparison of results between dynamic and static test(SY1 case)

表9 动载试验结果与静载试验结果对比统计(工况SY2)Tab.9 The comparison of results between dynamic and static test(SY2 case)
(1)同一测试工况下,动载试验测点应力最大值普遍大于静载试验值,增幅约20%~30%,个别测点增幅达到50%,这主要是由冲击载荷引起的,当臂架吊载突然反向回转时冲击载荷最大。在有限元计算时施加动载效应和侧向载荷后,与动载测试结果误差在10%~20%,动载和冲击载荷设定具有一定经验性,实际吊载过程未达到设置值。
(2)动载试验与静载试验确定的危险点位置基本一致,测点2-4、3-1及3-4应力较大,顶节与标准节连接处最危险,这与理论分析确定的危险区域相符合。
4 结语
本文建立300 t履带起重机臂架有限元模型,对比线性与非线性计算结果,可以看出结构的非线性特征比较明显,因此,按非线性方法进行有限元分析。根据对有限元结果的分析,获取常用工况下顶节、标准节、底节危险截面及应力分布规律。由此结合设计规范,制定应力测试方案及布置测点位置。通过对比测试结果与有限元计算结果,可以看出两者的数值差异较小,变化趋势相近,表明有限元模型建立的合理性和分析的正确性,为进一步的疲劳模型与计算提供参考。

