方柱微结构表面熔渣接触角的数值模拟研究
李立鸿,陈 豪,张泽飞,白 皓
1.汕头华兴冶金设备股份有限公司,广东 汕头 515063;2.饶平粤兴铜加工有限公司,广东 潮州 515726;3.北京科技大学 冶金与生态工程学院,北京 100083
钢铁生产中一些生产设备会受到高温熔渣的熔蚀,导致设备损坏[1].因此,降低熔渣对生产设备的熔蚀危害可提高设备的寿命.目前,可以采用涂覆陶瓷涂层的方法对设备进行高温防护.根据液固界面润湿理论[2],可考虑通过降低陶瓷涂层对熔渣的润湿性,减少熔渣在表面的停留,避免熔渣对设备表面的熔蚀,进而提高设备的寿命.目前降低液体润湿性的方法有两种,一种是在表面修饰低表面能物质,另一种是在固体表面制备微观粗糙结构.常用的低表面能物质使用温度在500 ℃以下,但设备工作环境在1000 ℃以上,而表面制备粗糙结构不受温度限制,因此可通过在涂层表面构造粗糙结构的方式降低涂层对熔渣的润湿性.
Young[3]提出了光滑表面上的液体润湿方程,但实际表面都存在粗糙度,Wenzel[4]和Cassie[5]根据Young提出的润湿理论,分别提出了在粗糙表面上的润湿模型,模型如图1所示.
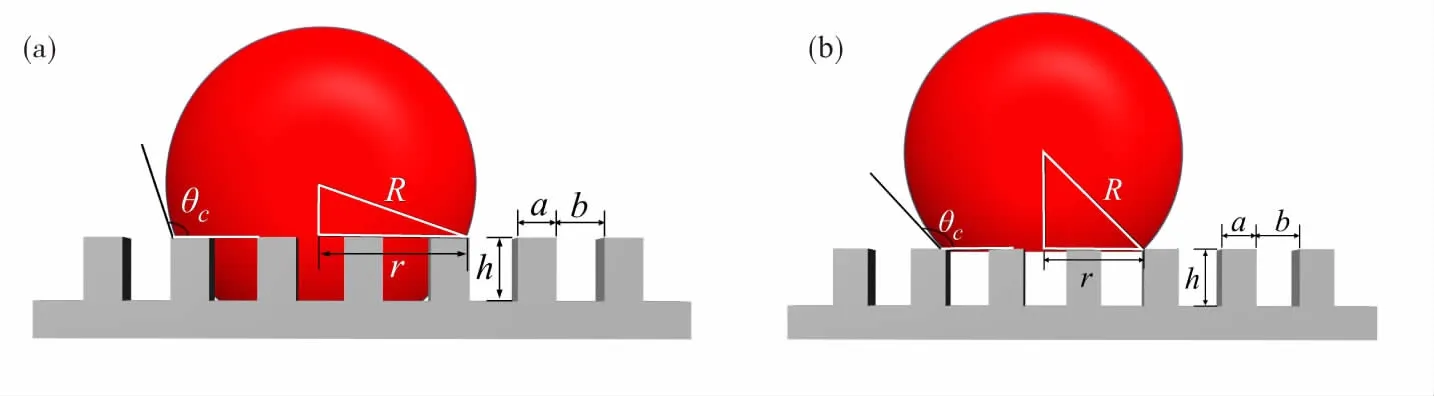
图1 润湿状态模型
Wenzel假设液体在均相粗糙表面上总是能够润湿粗糙结构间的凹槽,并提出了粗糙因子r,推导得到了液体在固体表面的表观接触角与粗糙因子及固体表面本征接触角之间的表达式,即cosθc=r·cosθa.式中θa为固体表面本征接触角,θc为粗糙表面的表观接触角,r为粗糙表面实际固液接触面积与投影面积的比值.Cassie认为表面由多种组分组成或液体不能完全润湿粗糙表面时,Wenzel方程将不再适用.当表面粗糙程度达到某一值时,液体不会完全充满凹槽,此时的固液界面由空气和固体构成,基于此假设Cassie推导得到润湿方程,即cosθc=f·cosθa+f-1,其中f为微结构上固液接触面积分数.潘贻芳等人[6]采用静滴法,研究了转炉渣与炉衬耐火材料的润湿性,解释了炉渣与耐火材料的粘附机制.程礼梅等人[7]总结了高温体系常见界面张力与接触角测量方法,并分析了温度与熔渣成分对熔渣润湿性的影响.
目前,关于熔渣在微结构表面润湿性能的相关研究报道较少.通过ANSYS Fluent二维数值模拟得到熔渣在方柱结构上的表观接触角,并与现有的接触角预测方程进行对比分析,为金属基陶瓷涂层的疏渣微结构的设计提供指导意义.
1 数值模拟
1.1 VOF模型及控制方程
目前界面追踪方法常用的有VOF法[8]、LBM法[9]、PIC法和两相流水平集法等,本研究采用Fluent软件中的VOF(Volume of Fluid)方法进行数值模拟.VOF法是通过相函数表示各相体积所占单元网格体积的比值,进而确定相界面的位置,该模型适用于追踪几种互不相溶合的流体界面,适用于自由表面流动、射流等.
VOF模型中,假设各单元中第i相体积分数为αi,则有:αi=0,单元中无i相;0<αi<1,单元为混合相;αi=1,单元全部为i相.
(1)
通过求解关于体积分数的连续性方程对气体与熔渣接触面的捕捉,体积分数的连续性方程微分形式:
(2)
动量方程微分形式如下,式(3)中Fj为包含表面张力及壁面粘附作用的源项.
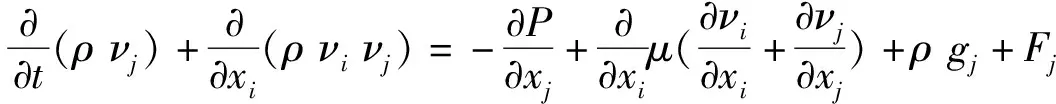
(3)
1.2 物理模型
本次模拟研究熔渣在具有不同方柱微结构涂层表面静态接触角的变化.将物理模型进行简化,即在方柱结构顶端放置一滴与顶端相切的熔渣,在重力作用下熔渣下落.模拟采用二维模型,计算区域尺寸为5 mm×5 mm,液滴直径为2 mm,其中a为方柱的边长、b为微结构间距、h为微结构高度,物理模型如图2所示.
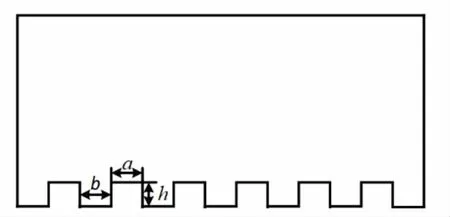
图2 物理模型
由于受到陶瓷涂层表面方柱结构加工工艺限制,方柱结构达到微米及亚微米级别较为困难,因此模拟时采用实际加工易于实现的方柱结构尺寸.选取方柱边长a=200 μm,高度h=150 μm,方柱间隔b选取五种不同的尺寸,定义k为方柱边长与方柱间隔之比,具体的方柱尺寸如表1所示.
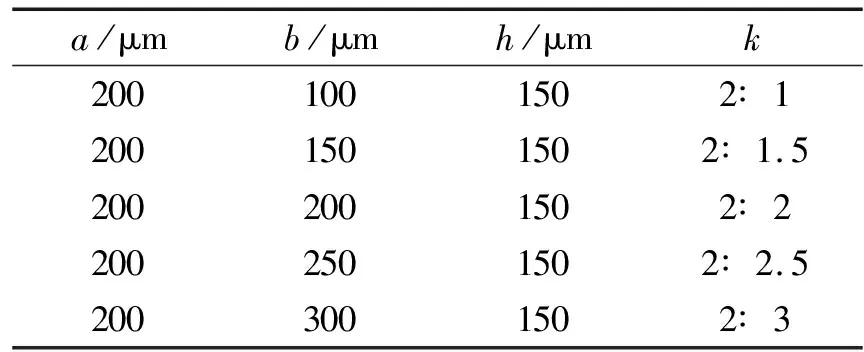
表1 方柱结构尺寸
1.3 熔渣成分及物性参数
模拟采用的熔渣是较为常用的高温熔渣,模拟中气体介质为空气.熔渣的成分和含量及物性参数分别列于表2和表3.由表3可知,陶瓷材料表面能约为0.1 N/m,高温熔渣的表面能要远大于陶瓷材料表面能.根据表面润湿理论,高温熔渣在光滑涂层表面的本征接触角应大于90 °,为此模拟时设置5个不同的本征接触角,5个本征接触角分别为90,100,110,120和130 °.

表2 熔渣成分
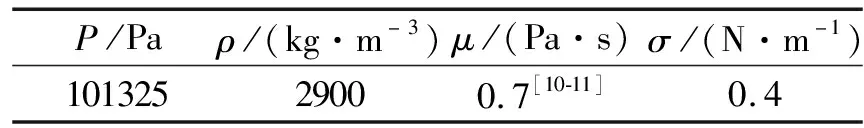
表3 熔渣物性参数
1.4 计算模型
计算域顶部采用普通无滑移壁面,下壁面为方柱微结构表面,左侧为压力入口边界条件,右侧为压力出口边界条件.模拟时设置熔渣置于微结构的涂层表面并与之相切的位置,熔渣在重力的影响下降落,最终达到稳定状态.图3为计算域和边界条件的示意图.
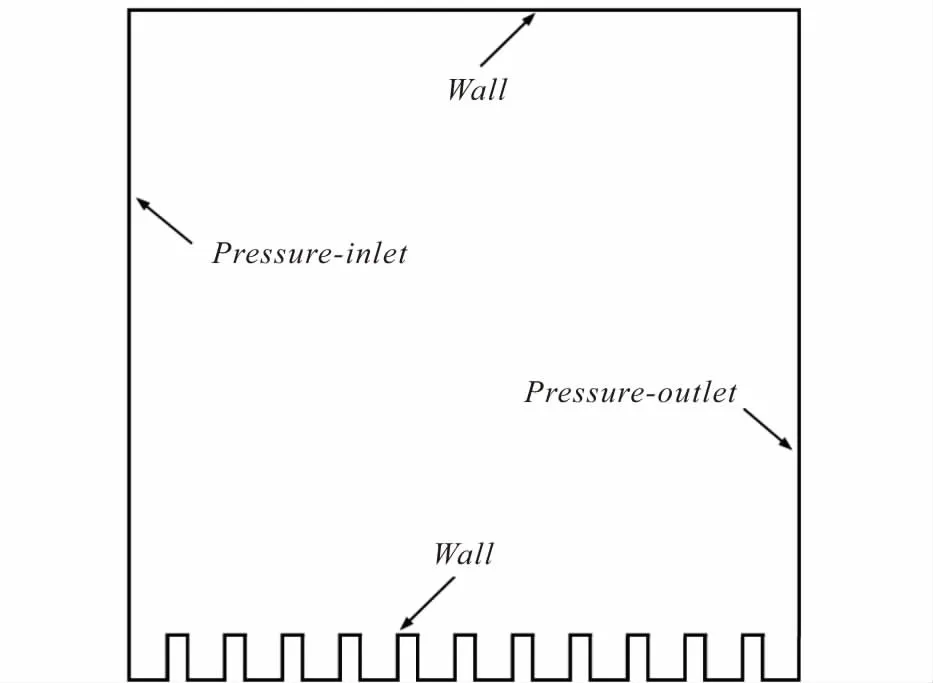
图3 计算域及边界条件示意图
1.5 模型验证
计算渣滴在具有方柱结构的涂层表面上的接触角前,需要对计算模型进行验证.验证模型采用光滑涂层平面进行验证,将5个本征接触角的值,在VOF模型中分别设置为光滑壁面与渣滴的接触角,其余边界条件与上述边界条件保持一致,计算完成后,测量熔渣与光滑壁面的接触角,进而判断计算模型是否可以使用.图4为熔渣在光滑壁面稳定后的形态.

图4 光滑表面熔渣接触角
对熔渣在光滑表面稳定后的形态进行测量,并与熔渣在光滑涂层表面的本征接触角比较,计算模型的误差值列于表4.
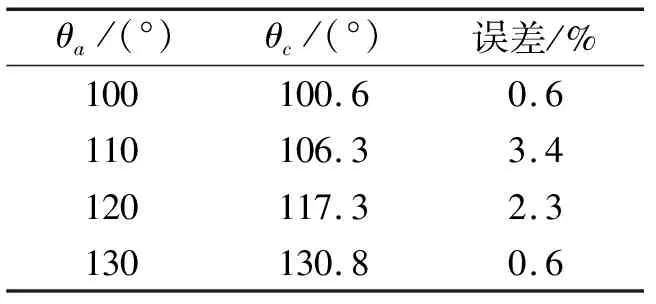
表4 模型误差值
由表4可知,使用VOF模型模拟熔渣在不同本征接触角的光滑涂层表面时,熔渣稳定时表观接触角的误差控制在3.5%以下,这说明使用VOF模型模拟熔渣在方柱微结构涂层表面的表观接触角是可行的.
2 结果与分析
对熔渣在不同k值的方柱微结构涂层表面上的形态进行模拟,得到熔渣在不同本征接触角的方柱结构涂层表面的稳定形态,其稳定形态如图5~图9所示.从图5~图9可以看到,熔渣在方柱结构上稳定后,方柱间隔内充满空气,熔渣保持在Cassie润湿状态.

图5 本征接触角为90°,各k值下熔渣在方柱结构表面稳定形态

图6 本征接触角为100 °,各k值下熔渣在方柱结构表面稳定形态

图7 本征接触角为110 °时,各k值下熔渣在方柱结构表面稳定形态

图8 本征接触角为120 °时,各k值下熔渣在方柱结构表面稳定形态

图9 本征接触角为130 °,各k值下熔渣在方柱结构表面稳定形态
将模拟结果与Cassie润湿状态接触角推导方程[12]所计算得到的表观接触角进行对比,表观接触角方程如式4所示.各本征接触角的对比结果及模拟误差值列于表5.
(4)
由表5可知:在涂层方柱结构表面上,熔渣稳定保持在Cassie润湿状态,且熔渣的表观接触角相比光滑涂层表面均增大;模拟结果与推导方程预测的接触角值较为符合,误差在10%以下.表观接触角作为衡量固体表面疏液性能的重要指标,涂层方柱结构表面熔渣表观接触角的提高,说明了在本征接触角θa≥90 °的涂层表面,方柱结构可以降低陶瓷涂层对熔渣的润湿性,提高了涂层疏渣性能.
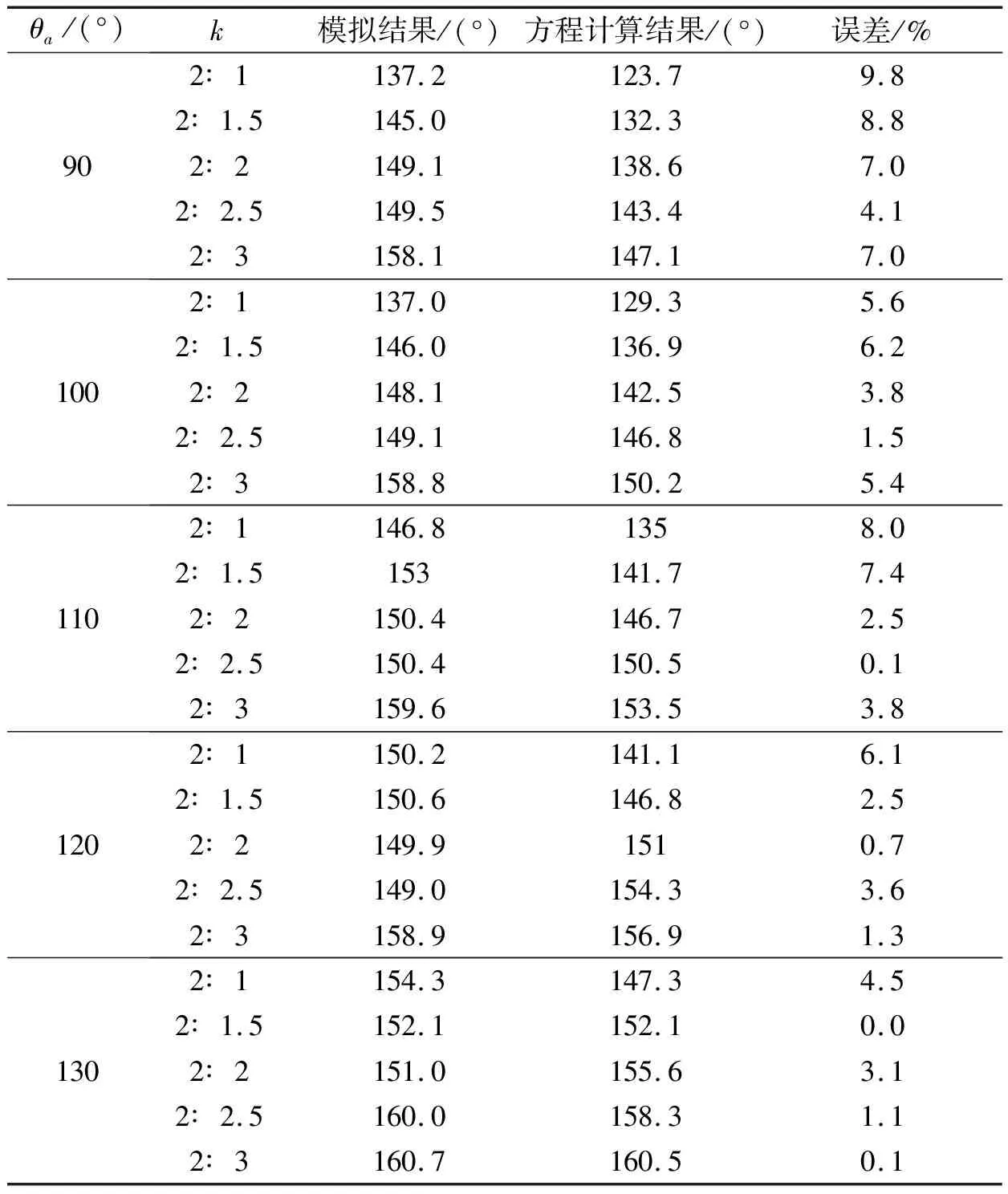
表5 表观接触角模拟计算结果与方程计算结果的误差表
目前,水在固体微结构表面润湿性的理论研究[13]及制备方法[14-16]均发展较为成熟,但对熔渣在微结构表面润湿性研究较少,这是由于熔渣本身具有高温性,目前的研究手段限制了对其润湿性的研究.熔渣与水相比,熔渣具有较高的表面张力和粘度.从理论上分析,熔渣的高表面张力和高粘度会使得熔渣在方柱微结构表面的接触角增大,且从模拟结果来看熔渣接触角均增大,与经典理论润湿模型的预测值较为符合.因此,在涂层表面构建方柱微结构的应用可以基于理论模型和模拟结果,对涂层表面构建方柱微结构进行指导,以期提高涂层表面的疏渣性能,改善熔渣熔蚀高温工作设备,损害设备寿命的问题.
3 结 论
针对钢铁企业中生产设备受到熔渣侵蚀的问题,以Wenzel和Cassie润湿模型为基础,使用Fluent中VOF模型对熔渣在不同本征接触角及不同方柱间隔的涂层表面上的接触角进行了二维数值模拟,对比分析了接触角方程计算得到的接触角与模拟得到的接触角之间的误差.
(1)模拟计算结果显示,在具有方柱结构的涂层表面熔渣均处于Cassie润湿状态.
(2)熔渣在方柱结构的涂层表面上,表观接触角相比光滑表面的均增大;
(3)模拟结果与接触角方程计算结果对比后发现,模拟结果较为符合方程计算结果,这将为陶瓷涂层表面方柱结构尺寸选择提供了重要理论依据.

