全风向角下双方柱脉动气动性能试验研究

杜晓庆，成文涛，董浩天，马文勇

（1.上海大学 土木工程系，上海 200444；2.上海大学 风工程和气动控制研究中心，上海 200444；3.上海大学 力学与工程科学学院，上海 200444；4.石家庄铁道大学 风工程研究中心，河北 石家庄 050043）

超高层建筑在大城市中常以群体建筑的形式存在，其周围流场存在复杂的气动干扰.在气动干扰影响下其风荷载和风致响应特征与单体建筑相比有着显著的区别[1-5].受上游建筑尾流旋涡的激励作用，下游建筑易发生风致振动，对其抗风性能造成不利影响[6].常以均匀来流中的双方柱作为群体超高层建筑的简化模型.双方柱绕流受众多因素影响，流场结构复杂，研究双方柱，特别是下游方柱的脉动气动性能有助于理解超高层建筑的气动干扰机理.

国内外学者对二维单方柱的气动力与流场结构已有了非常深入的研究[7-9]，其气动力与流场结构受风向角的影响显著，而受雷诺数的影响较小.对双方柱的研究则主要针对串列[10-13]及并列[14-17]两种布置形式，方柱间距比P/B（其中P 为柱心距，B 为方柱边长）对串列和并列方柱的表面风压、气动力和斯托罗哈数等气动参数影响显著.对于串列双方柱，Sakamoto 等[10]通过风洞试验观察到雷诺数Re=2.76×104和5.52×104时，存在临界间距比P/B=4，方柱气动力会在临界间距比附近发生突变.Yen 等[11]和Sohankar[12]根据间距比把串列双方柱绕流分为单一钝体、剪切层再附和双涡脱三种流态.对于并列双方柱，Alam 等[16]通过流迹显示和测力试验测量了Re=4.7×104时不同间距比并列双方柱的气动力和斯托罗哈数，按照P/B 的大小将并列双方柱绕流分为单一钝体、双频率涡脱、过渡转换和双涡脱四种流态.陈素琴等[17]通过数值模拟研究了Re=1×104时并列双方柱偏向流与气动力关系的机理.需要注意的是，既有研究较少关注间距比对双方柱，特别是下游方柱的脉动气动性能的影响.

针对风向角对双柱干扰效应的影响，Du 等[18]通过风洞试验研究了Re=8×104双方柱0°到90°风向角时平均气动力和风压分布的变化.Wu 等[19-20]通过数值模拟研究了Re=1.4×105时双圆柱的脉动气动力，发现在小风向角下（α=0°～30°）上、下游圆柱的脉动升力和流场特性变化剧烈，双圆柱会经历五种干扰流态.目前针对双方柱，尤其是下游方柱脉动气动性能在不同风向角下变化的研究仍属于空白.

本文针对双方柱中的下游方柱，通过同步测压风洞试验，在Re=8.0×104时测得其在风向角α=0°～90°和间距比P/B=1.25～5 时的表面风压，并进一步研究了不同间距比时下游方柱脉动气动力、升力功率谱、斯托罗哈数和气动力展向相关性随风向角的变化规律，最终为群体超高层建筑的抗风设计提供参考[21].

1 风洞试验

全风向角下双方柱测压风洞试验如图1 所示，在石家庄铁道大学风工程研究中心回流风洞高速段完成.试验风洞长5 m，高2 m，宽2.2 m，背景湍流度Iu≤0.2%.以方柱边长B 为特征长度，计算得到雷诺数Re=8.0×104，试验风速U=10 m/s.电子压力扫描阀的采样频率为330 Hz，采样时间约为36 s.

图1 双方柱风洞试验Fig.1 Wind tunnel test of two square cylinders

全风向角下双方柱的试验布置如图2 所示，其中α 为风向角，P 为柱心间距，方柱边长B=120 mm，CDf和CLf分别为脉动阻力系数和脉动升力系数.下游方柱的展向和环向风压测点布置分别如图3 和图4 所示.模型的展向长度为1 620 mm，长细比为13.5.沿展向布置了四圈测点（1，2，3，4），分别距下游方柱端部450 mm、670 mm、930 mm 和1 170 mm；每圈沿环向设有44 个测点，共计176 个测点.为减小端部效应影响，在方柱模型的两端设置了直径为1 m的端板.考虑了模型、端板、支架等影响后的面积阻塞率为5.3%.试验风向角α 为0°、2.5°、5°、7.5°、10°、12.5°、15°、17.5°、20°、25°、30°、35°、40°、45°、50°、55°、60°、65°、70°、75°、80°、85°、90°.试验的间距比P/B 分别为1.25、1.5、1.75、2、2.5、3、3.5、4、4.5、5.此外，还进行了相同条件下单方柱的风洞试验.

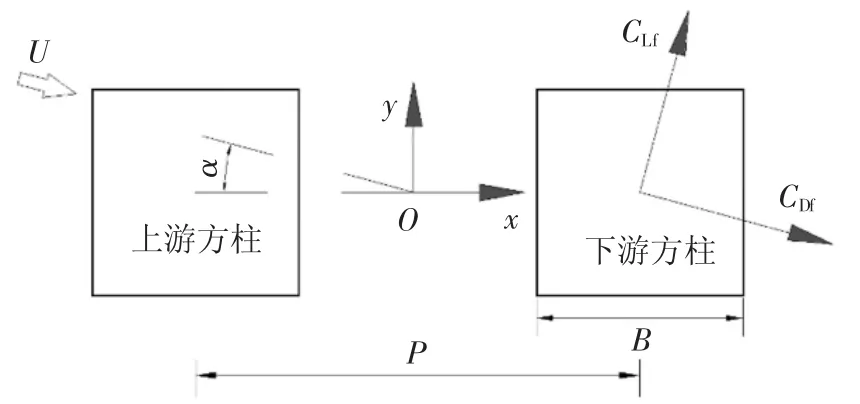
图2 双方柱的平面示意图Fig.2 Sketch of twin square cylinders

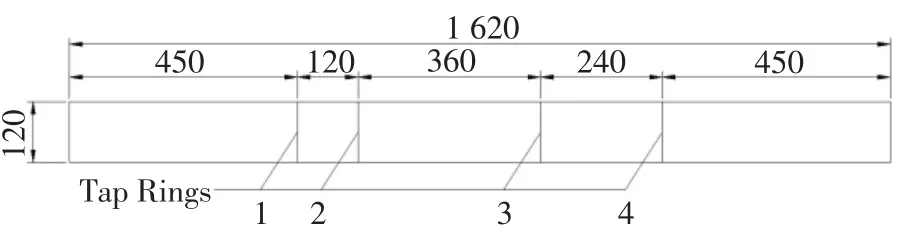
图3 下游方柱展向测点布置（单位：mm）Fig.3 Spanwise arrangement of pressure taps（unit：mm）

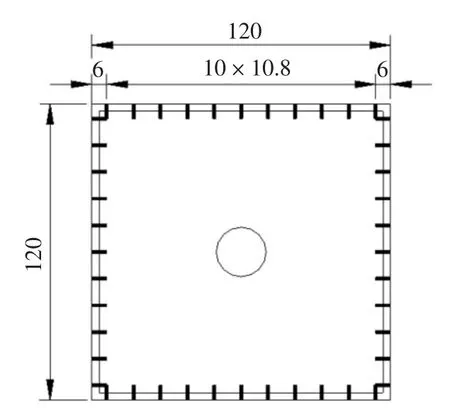
图4 下游方柱环向测点布置（单位：mm）Fig.4 Circumferential arrangement of pressure taps（unit：mm）

2 结果与分析

2.1 脉动气动力

图5 以云图的形式描绘了下游方柱脉动阻力和升力随间距比和风向角的变化，并以单方柱在不同风向角下的结果作为对照.对于脉动阻力系数，当P/B ＜3 时，下游方柱CDf很小，且在20°≤α≤90°时远小于单方柱；而3≤P/B≤5 且0°≤α≤30°时，下游方柱CDf远大于单方柱.对于脉动升力系数，P/B ＜3 时，下游方柱CLf较单方柱小；当3≤P/B≤5，0°≤α≤10°或80°≤α≤90°时，下游方柱CLf与单方柱大致相似.总的来看，下游方柱的脉动气动力系数在间距比P/B=3 前后有明显的不同.为更好地认识不同间距比时下游方柱脉动气动性能随α 的变化规律，下文选取P/B=1.25、3、5 三个典型间距比展开进一步分析.

图5 下游方柱在不同间距比和风向角情况下的脉动气动力云图与单方柱不同风向角结果对比Fig.5 Contours of the fluctuating aerodynamic coefficients on the downstream cylinder at various incidences and spacings

图6 反映了三个典型间距比的下游方柱脉动气动力随α 的变化.相对于单方柱，下游方柱的脉动气动力-风向角曲线的对称性较弱，且多数工况的CDf和CLf数值较小，体现了上游方柱对下游方柱的影响.

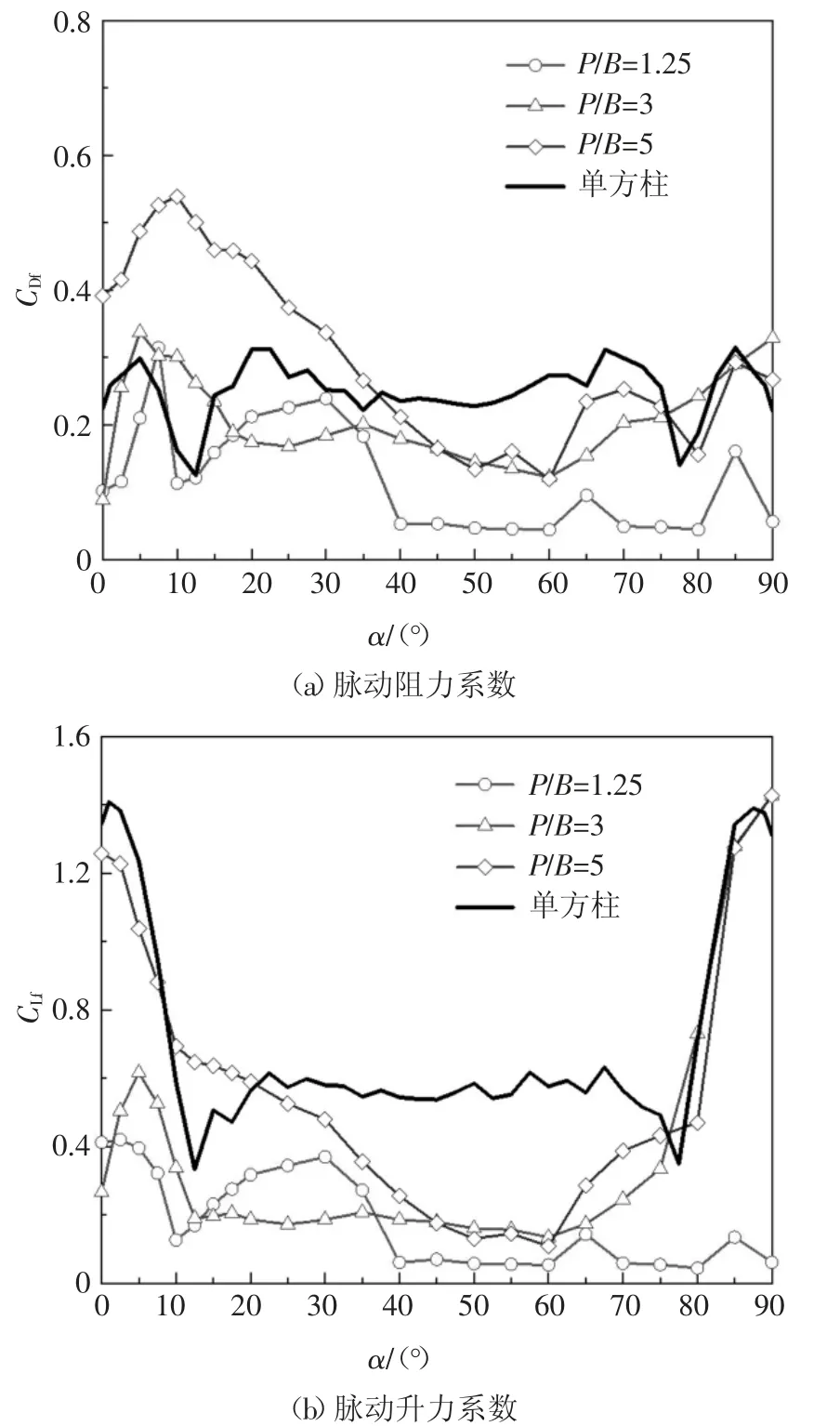
图6 典型间距比下游方柱和单方柱脉动气动力随风向角的变化Fig.6 Fluctuating aerodynamic coefficients on the downstream cylinder at typical spacing ratios

对于间距比P/B=1.25 的下游方柱，α≤35°时，CDf的变化接近单方柱结果；α≥40°时CDf数值很小且基本上不随风向角变化.CLf具有相似的变化规律，也在α=40°附近出现显著变化，可以推测下游方柱在临界风向角α=40°前后处于两种差异显著的流场之中.P/B=3 工况下游方柱脉动气动力同P/B=1.25工况有一定区别，40°≤α≤75°时CDf和CLf有所增大但整体上小于单方柱结果；α ＞75°时下游方柱的脉动气动力与单方柱基本一致，说明上游方柱对下游方柱的影响有所削弱.当间距比P/B=5 时，下游方柱的脉动气动力显著强于前面两种工况，甚至在部分工况强于单方柱；对于脉动阻力系数，α≤35°时远大于单方柱结果并在α=10°左右达到峰值，40°≤α≤75°时略小于单方柱结果，α ＞75°时则与单方柱结果趋于一致；对于脉动升力系数，CLf在α ＜25°或α ＞75°时同单方柱基本吻合，但在25°≤α≤75°时下游方柱结果小于单方柱，说明上游方柱对下游方柱的影响仍较强.

2.2 功率谱和Strouhal 数

图7 为单方柱和下游方柱的升力功率谱.根据下游方柱脉动气动力随风向角的变化规律，选取了5个典型风向角α=0°、25°、50°、70°和90°进行分析.对于单方柱，可以发现各个风向角下的升力功率谱曲线较为一致，峰值所对应的Strouhal 数几乎不随风向角的变化而变化.对于下游方柱，当间距比P/B=1.25 时，下游方柱的升力功率谱与单方柱有很大的不同，这是由于双方柱流场与单方柱流场的差异所导致的.下游方柱在α=0°下的升力功率谱曲线具有两个峰值，且对应峰值均较小.当风向角α=50°和70°时，下游方柱的升力功率谱曲线没有明显的峰值，说明在此风向角下，下游方柱的旋涡脱落受到较强的抑制；当间距比P/B=3 时，与间距比P/B=1.25相比，最明显的差异在于，当风向角α=50°和70°时，下游方柱的升力功率谱曲线又出现了峰值，说明上游方柱对下游方柱旋涡脱落的抑制作用减弱.同时，注意到升力功率谱曲线的双峰值现象也更为明显，这是由于下游方柱处于上游方柱的尾流之中，两个升力功率谱曲线峰值所对应的Strouhal 数分别对应上游方柱的涡脱频率和下游方柱的涡脱频率[18]；而当间距比P/B=5 时，下游方柱在各个风向角下的升力功率谱曲线更加接近单方柱，说明下游方柱在各个风向角下所处的流场与单方柱接近.

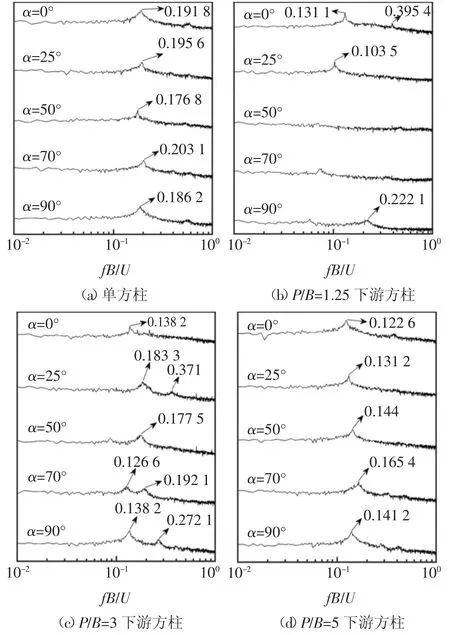
图7 单方柱与下游方柱升力功率谱Fig.7 Power spectrums of lift coefficients on a single square cylinder and the downstream cylinder

图8 给出了单方柱和三个间距比的下游方柱Strouhal 数随风向角的变化规律.单方柱的Strouhal数随风向角的变化幅度很小，涡脱频率较为固定.当间距比P/B=1.25 时，下游方柱的Strouhal 数整体很小，而当风向角α 接近90°时，Strouhal 数突然增大且接近单方柱；当间距比P/B=3 时，与间距比P/B=1.25 相比.下游方柱在相同风向角下的Strouhal 数较大，略小于单方柱，说明下游方柱在此间距比下的涡脱频率比较接近单方柱.当间距比P/B=5 时，下游方柱的Strouhal 数随风向角的变化规律与间距比P/B=3 相似.总的来说，不同间距比时下游方柱的Strouhal 数随风向角的变化规律有明显的差异；与单方柱相比，各个间距比下的下游方柱的Strouhal 数均较小，说明上游方柱对下游方柱的旋涡脱落有显著的抑制作用.

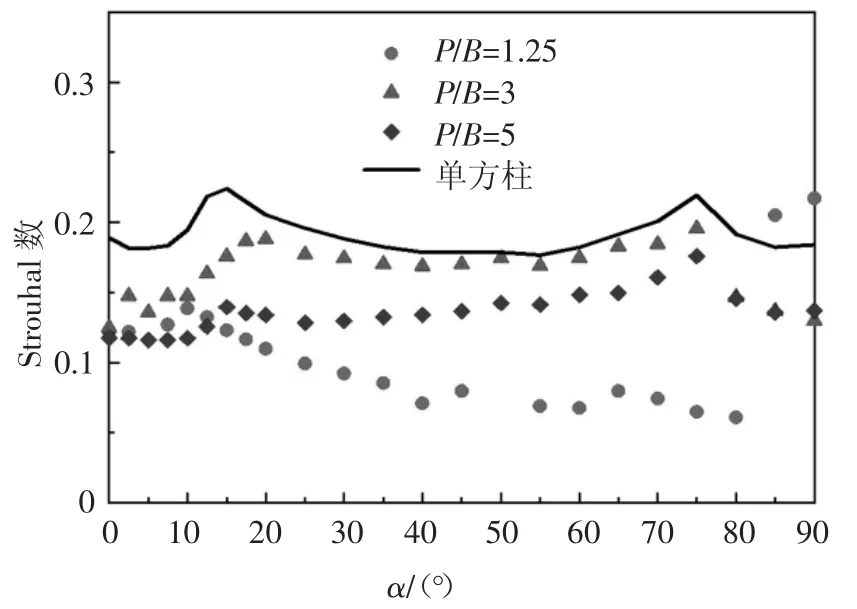
图8 下游方柱在不同风向角下的Strouhal 数Fig.8 Variation of Strouhal number with incidence angles for the downstream cylinder

2.3 气动力展向相关性

图9～图12 分别给出了单方柱、P/B=1.25 时下游方柱、P/B=3 时下游方柱和P/B=5 时下游方柱阻力和升力的展向相关性系数COR 随风向角α 和展向长度z/B（z 为不同测圈的展向间距）的变化.从图9 可知，对于单方柱，升力的展向相关性要强于阻力结果.当z/B 较小时，单方柱升力展向相关性基本上不随风向角变化.此外单方柱的阻力和升力的展向相关性曲线均大致关于α=45°对称.从图10 可知，P/B=1.25 下游方柱的气动力展向相关性曲线的对称性和数值均同单方柱差异显著.α ≤40°时，下游方柱的气动力展向相关性优于单方柱，且不同z/B 的结果较为接近，同时其对应的脉动气动力数值也较大.α ≥40°时，下游方柱的气动力展向相关性则弱于单方柱.值得注意的是在α=65°和85°存在两个展向相关性的极大值，而相同风向角下的脉动气动力也存在峰值.从图11 和图12 可知P/B=3 和5 情况下下游方柱气动力展向相关性随风向角的变化趋势较为接近，同P/B=1.25 结果差异较大.同风向角下，不同z/B 的气动力展向相关性相差较大.α=40°时，下游方柱的气动力展向相关性没有出现突变.当z/B 较小时，气动力展向相关性随风向角变化幅度较小，而随着z/B 增大，展向相关性随风向角变化明显.

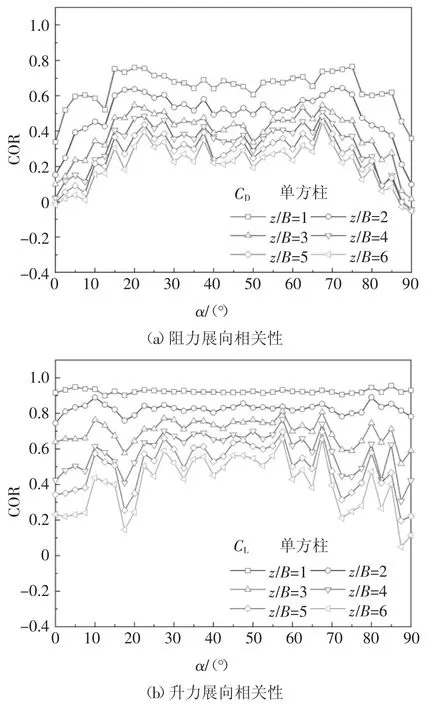
图9 单方柱气动力的展向相关性Fig.9 Spanwise correlations of aerodynamic force coefficients for a single cylinder

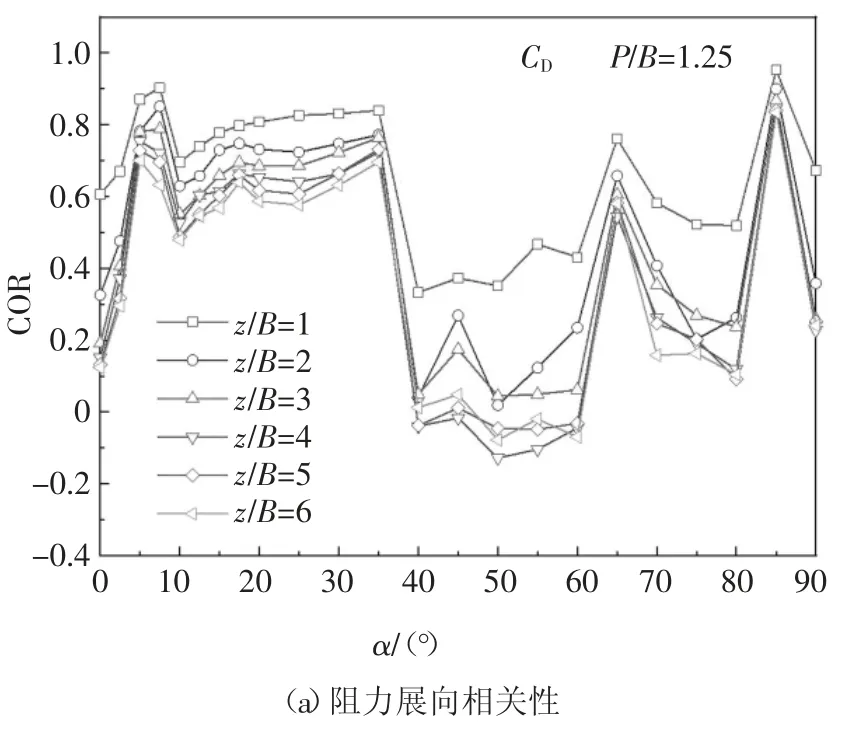
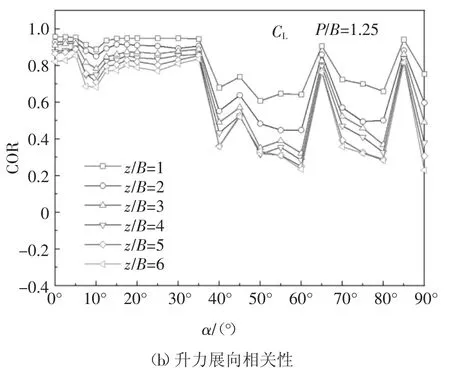
图10 P/B=1.25 工况时下游方柱气动力展向相关性Fig.10 Spanwise correlations of aerodynamic force coefficients for the downstream cylinder at P/B=1.25

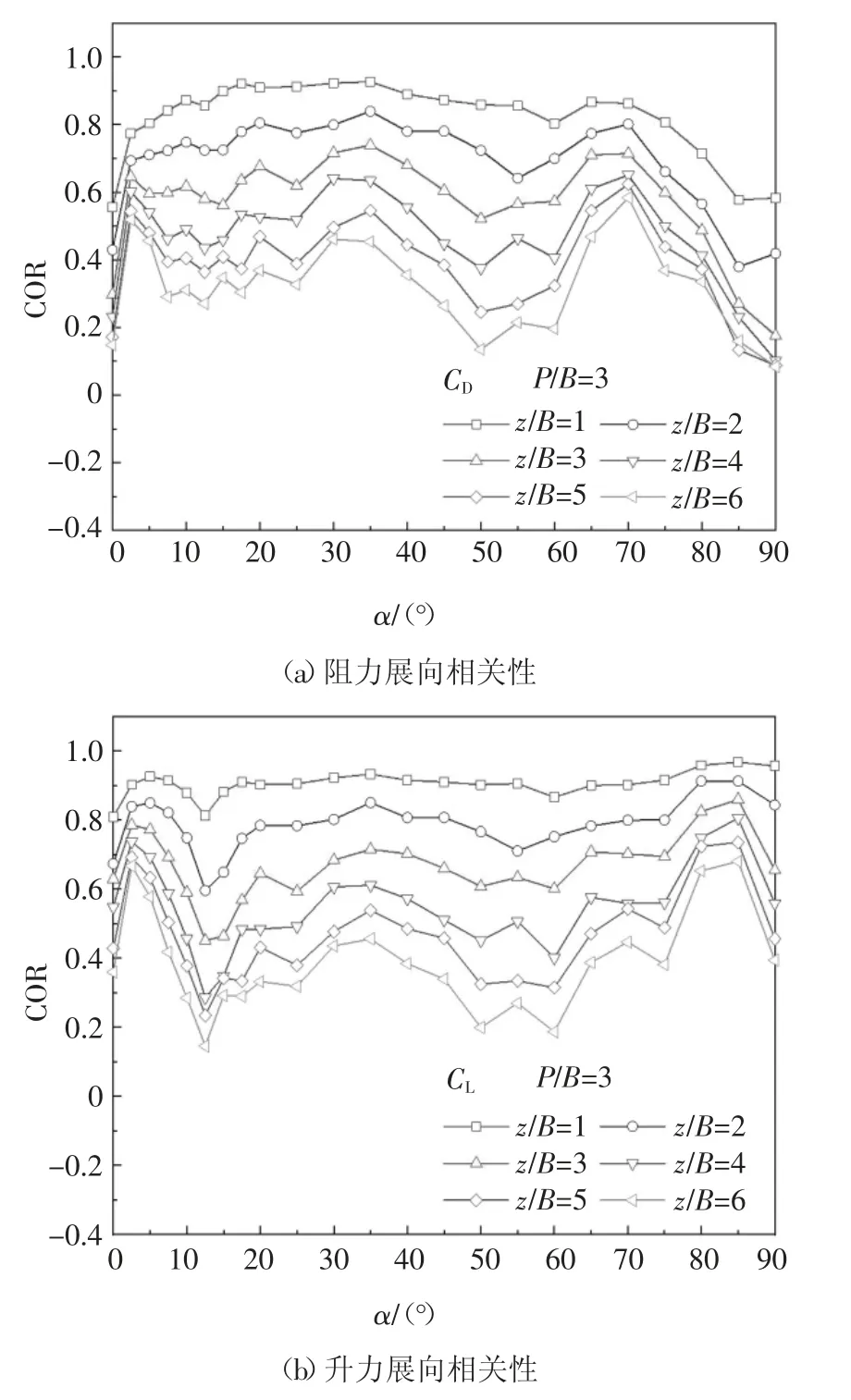
图11 P/B=3 工况时下游方柱气动力展向相关性Fig.11 Spanwise correlations of aerodynamic force coefficients for the downstream cylinder at P/B=3

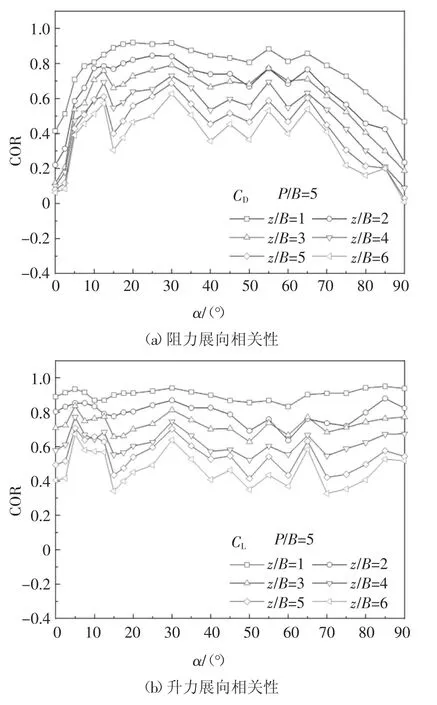
图12 P/B=5 工况时下游方柱气动力展向相关性Fig.12 Spanwise correlations of aerodynamic force coefficients for the downstream cylinder at P/B=5

3 结论

本文以双方柱中的下游方柱为研究对象，通过风洞试验研究了不同间距比全风向角下脉动气动力、升力功率谱和气动力展向相关性的变化，得到以下主要结论：

1）在小间距比大风向角情况下，下游方柱的脉动气动力远小于单方柱，且脉动气动力几乎不随风向角变化，上游方柱对下游方柱旋涡脱落的抑制作用显著.

2）在大间距比小风向角情况下，下游方柱的脉动阻力系数远大于单方柱，会对下游方柱的抗风性能产生不利的影响.

3）下游方柱的脉动气动力、升力功率谱特性和气动力展向相关性随风向的变化规律在间距比P/B=3 前后均体现出不同的特征.当间距比P/B ＜3 时，上游方柱对下游方柱脉动气动性能的影响显著，特别是在风向角较大的情况下，下游方柱旋涡脱落受到明显的抑制作用.当间距比P/B ＞3 时，下游方柱逐步摆脱上游方柱对它的气动影响，脉动气动力特性逐渐向单方柱转变.