组合优化算法改进的室内位置感知方法

韩学法，吴 飞，朱 海，时瑶佳

（上海工程技术大学 电子电气工程学院，上海 201620）

0 引言

随着科学技术的不断发展，基于位置的服务（location based service,LBS）的应用已经遍布生活中的各个方面，如车载导航系统、基于LBS的推荐系统以及其他应用系统，它们均采用了基于LBS的定位导航技术[1-2]。但是，这些应用在室外环境效果很好，在室内却无法进行精确位置识别，所以室内位置感知技术非常具有研究价值。由于无线局域网覆盖范围较广，无线保真（wireless fidelity,WiFi）定位技术能够满足人们对室内定位的需求，其最大的优势是成本低、计算开销小、定位精度较高[3-5]。因此，根据WiFi 信号进行室内移动目标位置识别的研究具有重要意义。

根据室内移动目标所处的环境信息进行室内场景准确识别，是基于位置服务的应用的技术关键。目前，基于位置感知的研究已成为学术界和工业界的研究热点[6-8]。现有的研究主要利用全球定位系统（global positioning system,GPS）、蓝牙、地磁、射频识别（radio frequency identification,RFID）、超宽带（ultra wide band,UWB）以及同步定位和制图（simultaneous location and mapping,SLAM）等信号源进行位置感知。但是，GPS 信号在室内环境中存在弱缺现象而无法满足人们室内定位的需求[9-11]；蓝牙定位技术仅适用于小范围的定位[12]；其他方法也存在各自的不足。文献[13]采用GPS信号进行移动用户的定位，但该方法适用范围有限，无法满足室内定位需求；文献[14]提出一种通过监视人们的日常行为进行位置估计的方法，这种技术在火灾等紧急情况中比较适用，但易受周边环境的干扰；文献[15] 提出了一种基于支持向量机（support vector machines,SVM）的位置识别算法，结合用户不同行走姿势进行位置感知，但是识别准确率低，定位均值误差达3.53 m；文献[16]提出一种基于神经网络的多传感器数据融合定位算法，能够对行人行走情况进行预判分类，但准确性不高；文献[17]利用机器学习方法，提出了一种适应多种环境的室内定位策略，但位置识别效果不是很好。

近来，对基于位置的服务的需求日益增加。尤其是在大型室内场所，这种移动目标的定位需求愈加强烈；研究室内移动目标的位置感知就显得尤为重要。为了解决现有研究方法的室内位置识别准确率较低、稳定性较差的问题，本文提出一种优化的室内移动目标的位置感知方法，通过采集用户在室内区域行走时智能手机接收到的周边接入点（access point，AP）的WiFi 信号数据，根据接收信号强度指示（received signal strength indicator,RSSI）值来建立位置指纹数据库，并将采集的数据作为样本对本文方法进行测试。

1 相关方法原理

1.1 粒子群算法

粒子群算法（particle swarm optimization,PSO）是文献[18]提出的一个典型的非线性的智能优化算法。PSO 受到觅食行为的启发，以群体和适应度为出发点，寻求解空间的最优解。PSO 算法就是基于目标优化的数学模型，具体定义为：

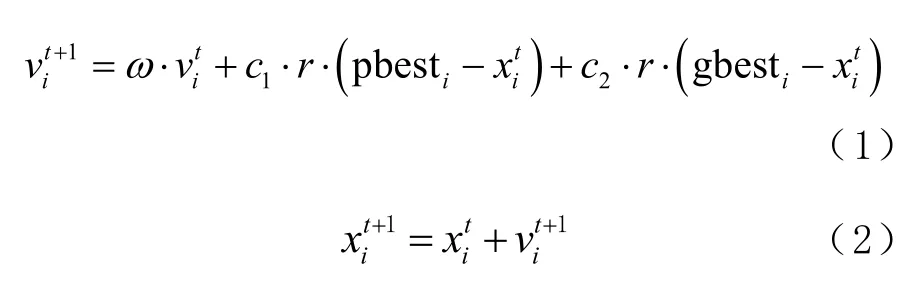
1.2 引力搜索算法

引力搜索算法（gravitational search algorithm,GSA）是由文献[19]提出的一种启发式优化算法，该算法是以万有引力定律和牛顿第二定律为基础，通过种群的粒子位置移动来寻找最优解。假设N个粒子构成一个搜索空间，则第i个粒子的位置定义为

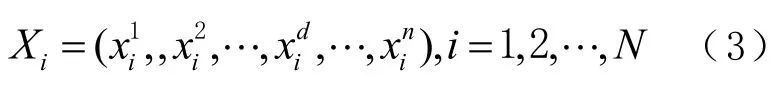
式中：N为搜索空间的维数；为第i个粒子在第d维空间的位置。

该算法首先将所有粒子随机放置在一个搜索空间中，在t次迭代运算时，粒子i、j间的相互引力定义为

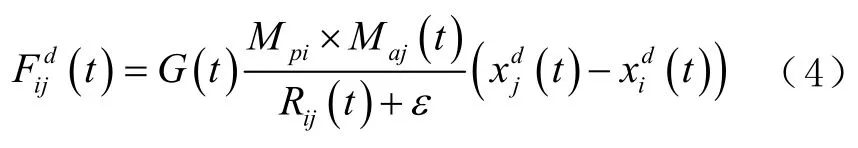
式中：Mpi和Maj分别为粒子i、j的惯性质量；ε为常数；G（t）为第t次迭代时的引力系数；Rij为粒子i、j的欧式距离。Gt和Rij的计算公式为：

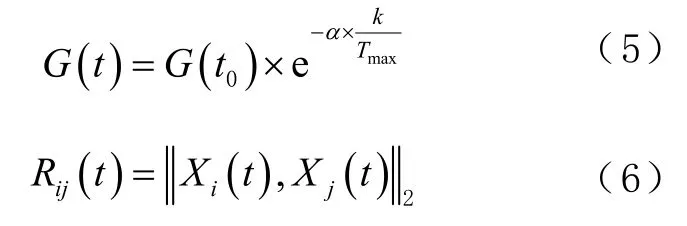
式中：G（t0）为引力系数初始值；α为引力系数；k为当前迭代次数。第i个粒子在第d维空间的引力计算公式为

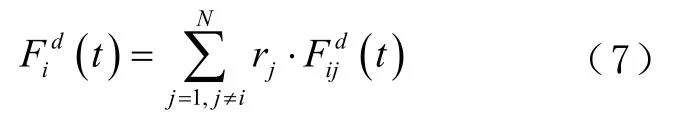
式中rj为分布于[0,1]的随机数。第t次迭代时，粒子i的加速度与合力成正比，引力质量成反比，其计算公式为

式中：t为迭代次数；Mi（t）为粒子i的引力质量。每次迭代时，粒子i的速度和位置迭代更新的计算公式为：

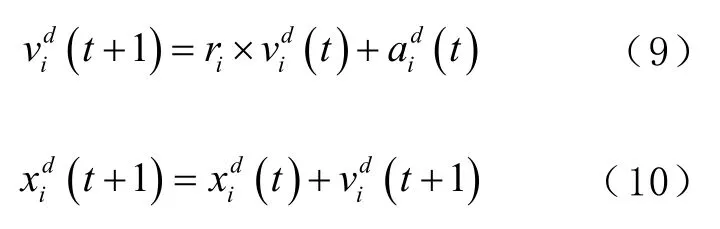
式中ri为分布于[0,1]的随机数。假设每次迭代时，粒子的引力质量与惯性质量相等，则第t次迭代时，粒子i的质量mi（t）迭代更新计算公式为

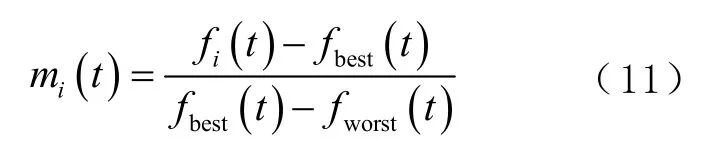
式中fi(t)为粒子i在t次迭代时的适应度值。对于最小值最优化问题，最优适应度值fbest(t)和最差适应度值fworst(t)的计算公式为

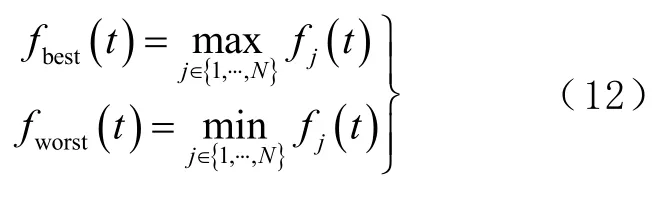
式中j表示粒子j。对于最大值最优化问题，最优适应度值fbest（t）和最差适应度值fworst（t）的计算公式为

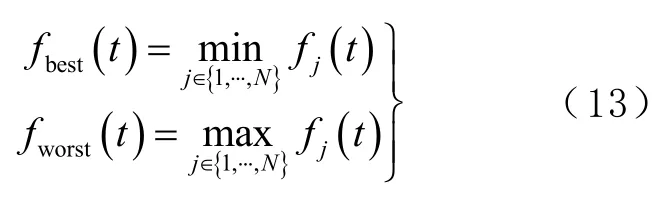
在实际应用过程中，粒子i的质量需要进行归一化，其计算公式为

2 改进的室内位置感知方法

2.1 改进的混合优化算法

由于PSO 算法的全局搜索能力强但速度较慢，而GSA 算法的局部搜索能力有限，它们各有所长，于是本文将二者结合起来，提出一种改进的组合优化算法，即PSOGSA 算法，以提高算法的适用性。

由式（9）和式（10）可知，GSA 算法仅保留迭代过程中当前位置信息，而无法在搜索过程中找到最优解，也就是说GSA 算法是一种缺失记忆能力的算法。本文结合PSO 算法全局搜索能力强的特点，对GSA 算法进行改进，增强其记忆搜索能力。整个搜索过程中，粒子运动方程为

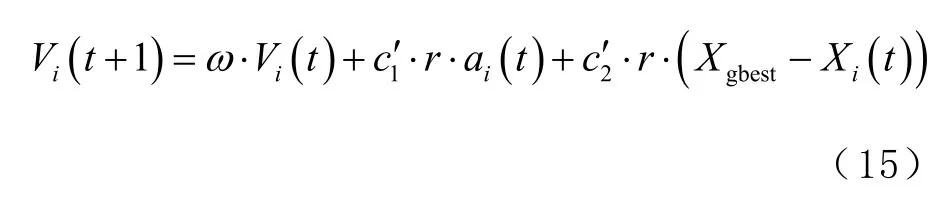
式中：V（it）是粒子i在第t次迭代时的速度；为加速度系数；Xgbest为粒子i在迭代过程中位置的最优解。则权重系数的计算公式为

式中：ωmax和ωmin分别为ω的上下限；Tmax为迭代次数的上限。PSOGSA 算法实现过程如图1 所示。

图1 PSOGSA 算法实现过程

2.2 基于PSOGSA-NN的位置感知模型

神经网络（neural network,NN）是一种易于理解且使用广泛的模型，该模型可以使用反向传播（back propagation,BP）算法进行预测分类[20]。对于室内定位来说，准确高效地识别出行人等移动目标的位置很关键。因此，本文将采集到的WiFi信号覆盖区域的RSSI 值作为位置指纹特征，以移动用户所在的位置区域作为分类标签，构建样本数据集，且样本数据集定义为

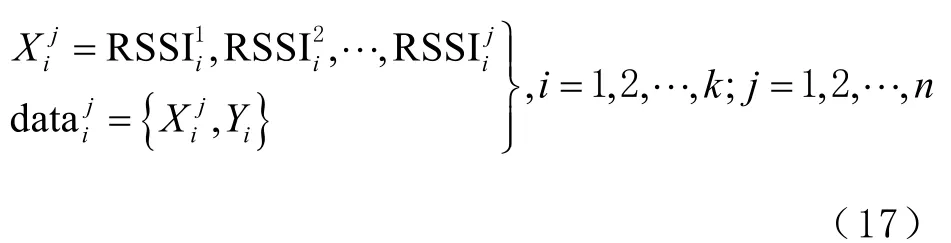
式中：i、j分别为区域位置的数目和AP 个数；为在第i个区域采集到第j个AP的RSSI 值。基于神经网络的室内位置感知模型主要包括输入层、隐含层和输出层，具体的模型结构如图2 所示。

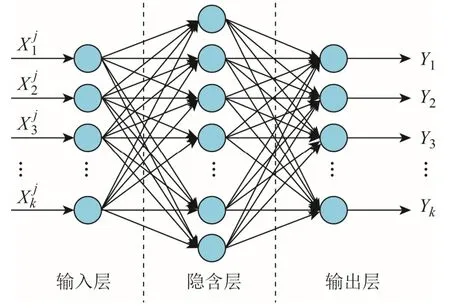
图2 室内位置感知模型

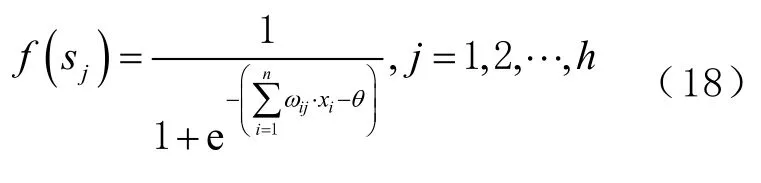
式中：fi为粒子i当前的适应度值；fmin和fmax分别为粒子i最大和最小适应度值，其实就是将每个粒子的适应度值归一化。θ的计算公式如下：

式中Vtc为第t次迭代时粒子当前的速度。

在室内定位中，通过sj和θ可以确定ω′，从而提高室内位置感知模型的识别率和准确率。基于PSOGSA-NN的位置感知模型如图3 所示。

由图3 可知，基于PSOGSA-NN 位置感知模型的核心是PSOGSA-NN 算法，该算法的具体实现过程如图4 所示。

图3 基于PSOGSA-NN的位置感知模型

图4 PSOGSA-NN 算法实现过程

3 实验与结果分析

3.1 实验环境

为了验证本文所提方法，选择某实验大楼中4个较为空旷的教室作为实验区域进行定位实验。实验场地的平面示意图如图5 所示。

实验人员手持装有自主开发的信号采集软件GetSensorData2.1的智能手机，行走在实验区域内，采集实验区域周边AP的WiFi 信号。

3.2 数据采集与处理

实验人员通过采集实验区域周边AP的RSSI值来构建位置指纹数据库，从而得到实验所需要的样本数据集。实验时，实验人员右手手持P30 智能手机于胸前，行走在实验区域进行WiFi 信号采集。采集过程中，频率均为50 Hz，数据采集界面如图6 所示。

实验时，分别采集房间1～房间4的数据，每个房间采集500 次，每次取接收到AP 信号的RSSI均值作为位置指纹，实验区域的RSSI 信号变化如图7 所示，图7（a）～图7（d）分别为房间1～房间4的RSSI 信号变化情况。

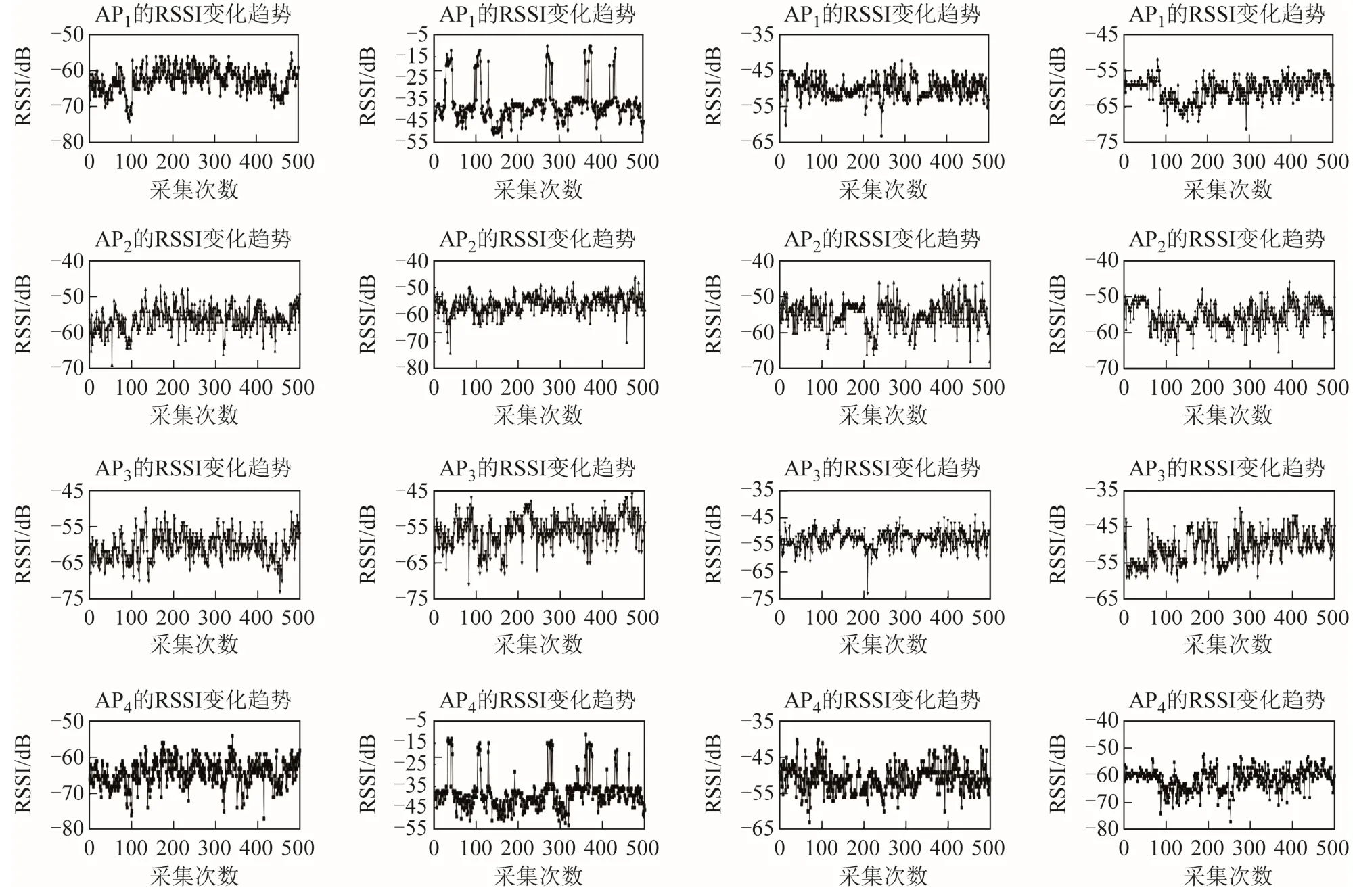
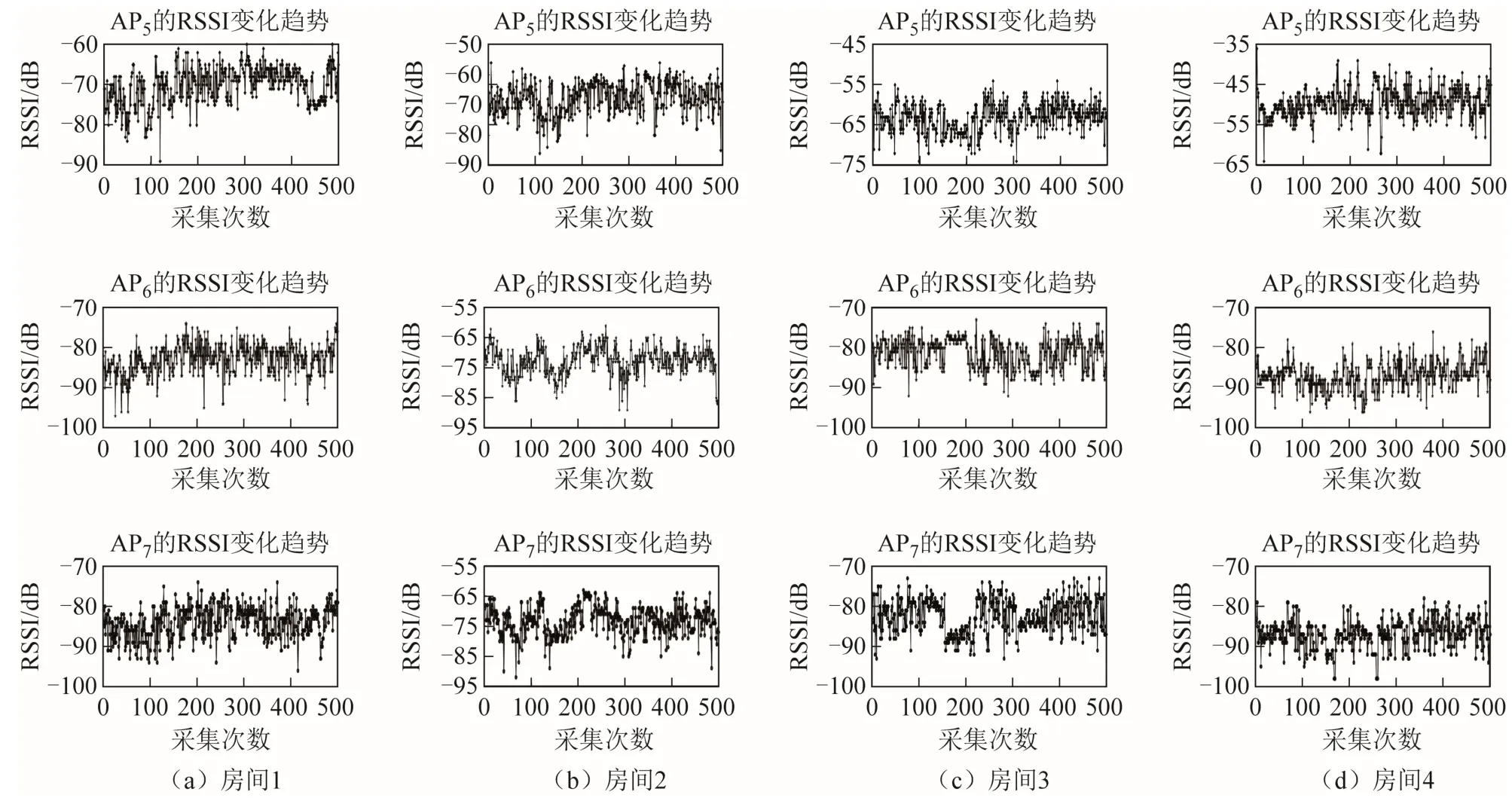
图7 不同房间的RSSI 信号变化

由图7 可知，不同位置的RSSI 信号存在差异，即RSSI 信号存在空间差异性，故可通过位置指纹来进行区域识别。数据经过处理后，每个房间仅保留500 条位置指纹样本，部分位置指纹样本信息如表1 所示，前7 列为RSSI 值，单位为dB，最后一列为房间类别编号。

表1 不同房间的位置指纹样本信息

3.3 结果分析

为了进一步验证本文方法的可行性，将2 000 条样本数据分为2 个部分，1 400 条作为训练集，600 条作为测试集。在机器学习中，ROC（receiver operating characteristic）即接收器操作特征曲线是用来描绘学习器的泛化能力的有力工具；而AUC（area under ROC curve）即ROC 曲线下的面积，用来度量分类模型的好坏。本文实验过程中，通过绘制不同类别的 ROC 曲线来进行模型评估，用AUC 作为模型评价指标。对于分类问题，也常用分类准确率作为评价指标。对于本文的位置感知识别准确率（racc）的定义为

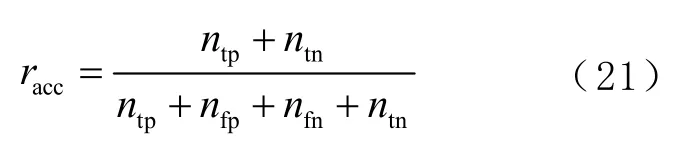
式中：ntp为预测房间类别与真实房间类别一致的样本数；nfp为预测房间类别与真实房间类相反的样本数；nfn为将预测错误的房间分类结果作为正确结果的样本数；ntn为将预测正确的房间分类结果当作错误结果的样本数。在ROC 曲线中横纵坐标分别为假正率（rfp）和真正率（rtp），它们的定义公式为：

为了进一步评价本文所提方法的性能，通过实验得出如图8 所示的效果。

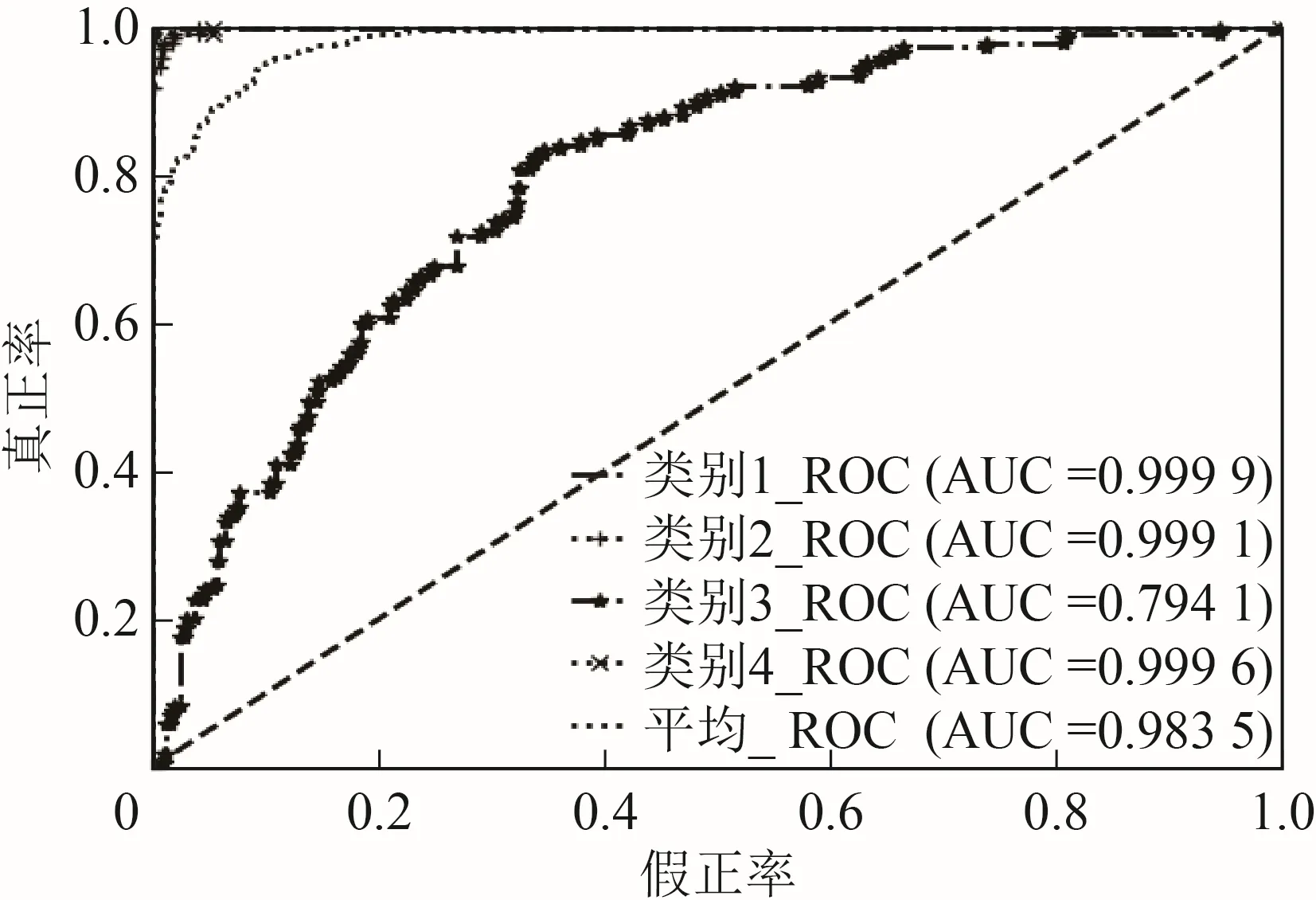
图8 本文方法的效果

由图可知，本文方法在室内的识别准确率较好，房间1 为99.99%，房间2 为99.91%，房间3 为79.41%，房间4 为99.96%，且平均准确率为98.35%。为了对比分析本文提出模型的效果，将本文模型（PSOGSA_NN）与支持向量机（SVM）分类算法、纳伊夫·贝叶斯（Naïve Bayes）分类算法、神经网络（NN）分类算法、粒子群-神经网络（PSO_NN）算法及引力搜索-神经网络（GSA_NN）算法进行对比，各类模型的识别准确率（所有类别的识别率的均值）如图9 所示。

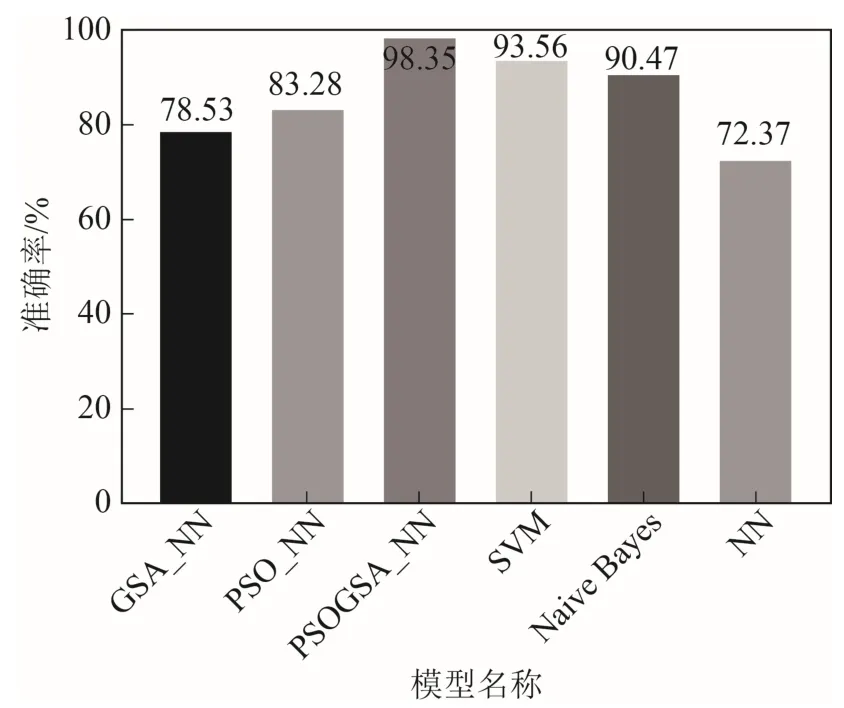
图9 模型对比的效果

由图可知，与同类方法对比，本文方法的位置感知识别准确率为 98.35%，比 SVM 算法高4.79%，比Naïve Bayes 算法高7.88%，比NN 算法高25.98%，比PSO_NN 高15.07%，比GSA_NN高19.82%。因此，本文方法的室内位置感知识别效果最佳，与同类方法相比，识别准确率至少提高4.79%。

4 结束语

为了解决现有研究方法的室内位置识别准确率较低、稳定性较差的问题，本文提出一种基于组合优化算法改进的室内位置感知方法。通过采集用户在室内区域行走时智能手机接收到的周边AP的WiFi 信号数据，根据采集的RSSI 值来建立位置指纹数据库，将采集的数据作为样本对本文方法进行测试。实验结果表明本文方法的室内位置感知识别准确率为98.35%，与同类方法相比，识别准确率至少提高4.79%。由于本文所进行的实验是以位置区域类别作为位置标签，AP的RSSI 值为位置特征，且位置标签是已知的，所以具有应用局限性。下一步将研究如何在位置未知的情况下进行室内位置识别，从而提高模型的适用性。