新疆陆态网络坐标时间序列噪声模型分析

隋哲民，李建章，佟雪佳，高志钰

（1.兰州交通大学 测绘与地理信息学院/地理国情监测技术应用国家地方联合工程研究中心/甘肃省地理国情监测工程实验室，兰州 730070；2.中国地震局地质研究所 地震动力学国家重点实验室，北京 100029）

0 引言

迄今为止，我国大陆构造环境监测网络即陆态网络（crustal movement observation network of China,CMONOC）的连续运行参考站（continuously operating reference stations,CORS）积累了数量可观且连续的原始观测数据，通过分析目标测站坐标时间序列的原始数据可以求出相应地区板块的速度场，进而为地壳形变研究以及地震分析预报等提供坚实的数据基础[1]。自新疆地区陆态网络建立完成后，许多国内外专家学者对该地区的坐标时间序列数据做了大量的相关研究，并建立了各自不同的速度场模型。文献[2]通过对新疆加密帕米尔东北侧地区的全球定位系统（global positioning system,GPS）监测网的解算与复测，得到了该地区地壳形变速率图及GPS基准站的时间序列[2]。文献[3]通过PODAP 软件解算2011—2014 年间3 a的新疆陆态网络连续站时间序列，得到了相应的速度场，发现新疆西南部至东北部，基准站的南北分量总体呈现递减的趋势，东西分量呈现出先递增后递减再次递增的拱形变化趋势[3]。文献[4]采用最小二乘法来配置并估计随机信号，在解算数据时引入赫尔默特（Helmert）方差分量估计来建立精度更高的速度场模型[4]。但是，由于新疆地区陆态网络建立时间较晚，导致上述研究并未对较长时间段即5 a 以上的时间序列及其有色噪声进行分析研究。倘若忽视所得坐标时间序列数据中存在的噪声，将无法有效分离有色噪声与观测得到的时间序列数据，进而会对速度场的解算产生很大的影响。文献[5]研究结果证实，要想获得较为可靠且稳定的时间序列最优噪声模型，至少需要积累超过5 a的时间序列观测数据[5]。为此，本文选取新疆31 个陆态网络连续站2010—2020 年间10 a的时间序列观测数据进行研究，确定3 个方向分量的最优噪声模型类型及其各自所占比重，进而得到新疆地区经最优噪声模型改正后基于国际地球参考框架（international terrestrial reference frame,ITRF）下的速度场。新疆时间序列最优噪声模型的确定可为新疆高精度坐标框架的研究提供参考，并为板块运动、地壳形变监测研究，以及新疆地区生产建设等提供思路。

1 噪声分析方法

目前，测绘工作者大多采用卡茨（CATS）软件以及赫克托（Hector）软件来分析GPS 坐标时间序列噪声，其中CATS 软件主要采用极大似然估计法（maximum likelihood estimation,MLE）来分析GPS 坐标时间序列的噪声特征。由于该款软件解算时间序列时所采用的算法以及相应的模型都较为准确，故能满足测绘工作者在解算时间序列数据时的精度需求，但是此软件在处理较大量的数据时，解算数据的速度十分缓慢，无法给实际工作提供便利[6]。为了克服此类难题，能够既好又快地处理大量的时间序列数据，2012 年，葡萄牙研究人员Bos 等人开发了Hector 时间序列分析软件，该款软件通过改进算法使得数据处理速率得到了大幅提升[7]。这种经过算法优化后的极大似然估计法即为贝叶斯信息准则（Bayesian information criterion,BIC）数值分析法。

1.1 极大似然估计法

以往在进行时间序列分析时普遍使用极大似然估计法，利用此类估计方法可以求解时间序列数据中所包含的绝大部分参数，例如截距、偏移、斜率、振幅等。故GPS 坐标时间序列一般可以表示[8-10]为

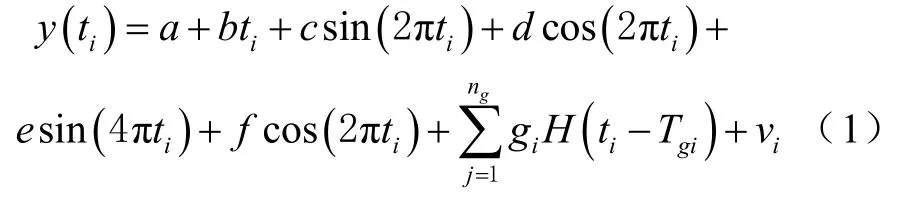
式中：ti表示儒略日（modified Julian date,MJD）时间，单位为年；a为站点起始地壳位置参数；b为时间序列中线性变化的速率；年周期和半年周期的振幅分别使用参数c、d、e、f来表示；H（t）表示阶跃函数（heaviside step function）；T指代发生阶跃的时刻；参数gi指代同震偏移（offset）；vi表示观测结果的残差，即当原始观测值与预期结果不同时所产生的偏差[6]。

1.2 BIC 数值分析法

Hector 软件可以用来估计线性趋势项、高阶多项式、季节项、其他周期项信号以及多种噪声模型的组合。在解算最优的噪声模型时，Hector 软件采用BIC 信息判别准则[7]，该准则是评价统计模型拟合结果优良性的一种标准；采用对数似然函数来解算数据，并在解算过程中添加参数k来避免过度拟合。此对数函数的定义为

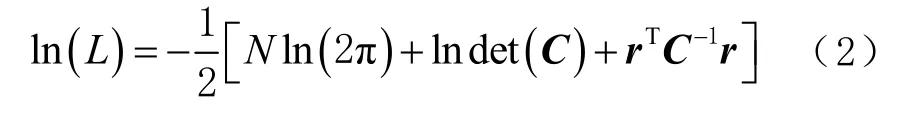
式中：N为实际观测数据的数量（不包括缺失的数据）；r为由观察残差和遗漏残差所组成的残差矩阵；协方差矩阵C可分解为

式中：σ为残差序列的标准差；为各类噪声的总和。σ的计算方法为

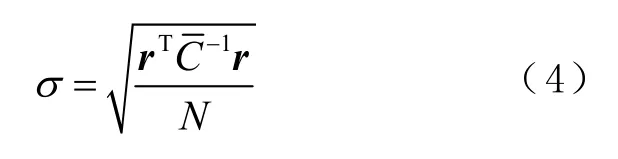
由det 可求已知常数C及N阶矩阵A的行列式，又detA=CNdetA，故联立式（2）、式（3）、式（4）可得

通过式（5）可以大致了解所估计的模型的复杂程度以及该模型所拟合数据的准确性，具体定义为

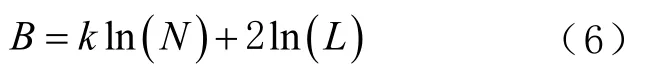
式中：B为所求BIC 值；k为模型参数的个数。

似然函数L越大，对应的模型越优，即具有（相对）最小BIC 值的模型为最优模型。在对不同组合模型进行解算后，比对这些模型的BIC 值，进而可以得到最优的组合噪声模型。

2 时间序列分析

实验选取中国新疆31 个CMONOC 连续站2010—2020 年的原始时间序列数据。采用Hector软件对原始时间序列数据剔除奇异值后进行最优噪声模型分析，并求出各假设模型相应的BIC 值。最后根据贝叶斯准则确定最优噪声模型，在得到最优模型的基础上对新疆陆态网络连续站的速度场进行修正。

2.1 时间序列获取

中国大陆构造环境监测网是中国地壳运动观测网的延续，在新疆境内，总共设置了31 个站点，测站具体分布如图1 所示。选取加米特（GAMIT）/格洛布克（GLOBK）软件[11]解算得到的基于ITRF14 框架下的原始坐标时间序列数据进行解算，具体流程可参考文献[12]。由于同一测站在不同长度时段内所求最优噪声模型、速度场差别较大，在研究分析测站最优噪声模型、速度场前需要指定该时间序列的时段[13]。本文所使用的数据来源于中国地震局全球卫星导航系统（global navigation satellite system,GNSS）数据产品服务平台[14]。

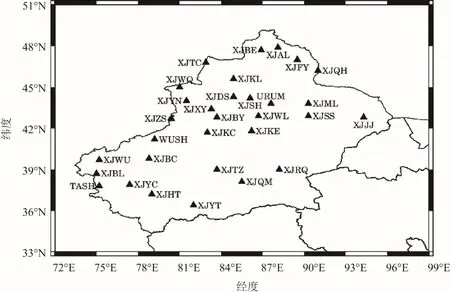
图1 新疆维吾尔自治区境内CMONOC 测站分布

由于篇幅有限，仅绘制XJBY、XJKE、XJYC 3 站的原始时间序列图像，如图2～图4 所示。从图2～图4 可以看出，N(北）、E(东）方向分量观测数据具有明显线性变化趋势：N 方向随时间的变化而递增且斜率较大；E 方向随时间的变化而递增且斜率较小；U（天顶）方向的变化趋势存在一定的周期性，且以1 a 周期来看最为显著。原始时间序列观测数据中存在明显的奇异值（或称为外野值），必须在数据处理前对其进行剔除。

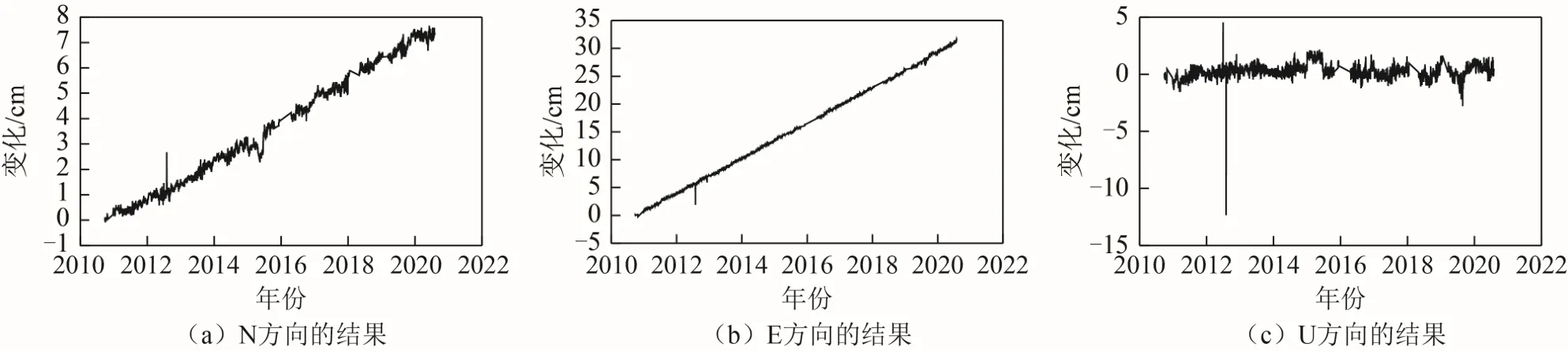
图2 XJBY 站原始时间序列

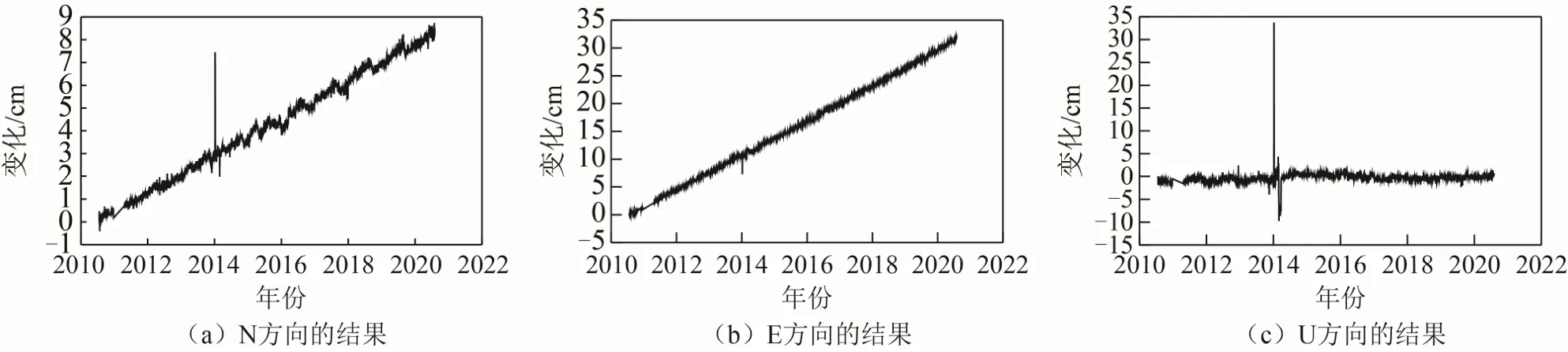
图3 XJKE 站原始时间序列

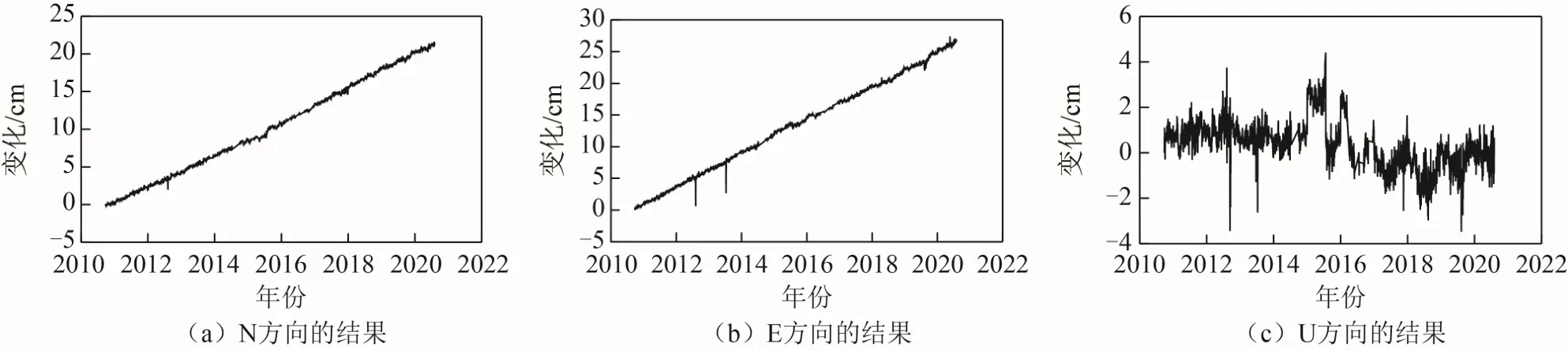
图4 XJYC 站原始时间序列

2.2 原始时间序列处理

Hector 软件剔除时间序列奇异值是首先使用最小二乘法估计原始坐标时间序列的线性趋势、周期性趋势，并去除线性趋势和周期性趋势以计算残差，然后利用四分位数粗差探测方法对残差进行剔除。其具体步骤为：①基于最小二乘法，利用式（1）获取残差时间序列；②基于残差时间序列，利用四分位距探测原始数据所包含的粗差，并剔除其中的奇异值；③重新拟合新获取的残差时间序列并重复步骤②，直至粗差完全剔除[7]。图5～图7 为XJBY、XJKE、XJYC 站数据处理后的时间序列图像。

图5 XJBY 站数据处理后的时间序列

图6 XJKE 站数据处理后的时间序列

图7 XJYC 站数据处理后的时间序列

2.3 最优噪声模型的确立

通过Hector 软件对全部31 个连续站3 个方向分量的数据进行解算，使用白色噪声（WN）分别与闪烁噪声（FN）、随机漫步噪声（RW）、幂律噪声（PN）和一阶高斯马尔科夫噪声（GGM）进行组合。进而使用这4 种组合模型计算出每个站所对应的N、E、U 3 个方向的BIC 值，然后在同一分量中找到每个测站所对应的最小BIC 值。其中，XJBC、XJBY、XJKC、XJKE、XJYC、XJYN 站在N 方向上噪声模型解算得到的BIC 差值如图8 所示。

图8 不同测站N 方向上各噪声模型的BIC 差值

通过比对不同模型的BIC 值，可获悉各测站每个方向分量的最优噪声模型。全部测站不同方向的最优噪声模型所占百分比如表1 所示。

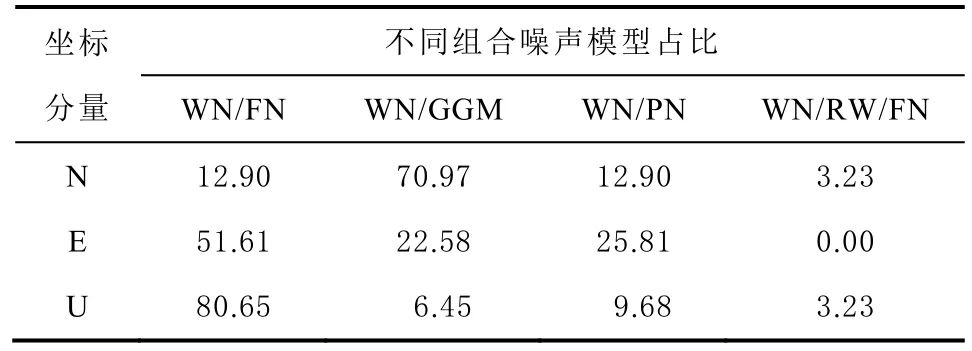
表1 各方向上最优噪声模型所占百分比 %

由表可知3 个方向分量时间序列与最优噪声模型之间的关系，且N 分量和E 分量、U 分量具有不同的噪声特性：在N 方向上，最优噪声模型为组合模型“WN/GGM”；在E 方向和U 方向上，最优噪声模型为组合模型“WN/FN”。

3 顾及最优噪声模型的新疆速度场分析

3.1 未经修正的速度场模型

绘制未考虑最优噪声模型改正的ITRF14 框架下新疆境内CMONOC基准站的水平运动速度场，如图9 所示。新疆东部运动方向近E 向，而西南部地区为EN 向运动。未修正的新疆陆态网络基准站在ITRF14 框架下水平方向运动的平均速率为30.966 mm/a，运动方向为NEE73°26′06″。

表2 给出了经修正后ITRF14 框架下新疆境内CMONOC基准站的水平方向速度估值和中误差统计结果。另外，31 个连续站的统计结果表明，E 方向速度的标准差为2.199 mm，N 方向标准差为6.384 mm，本文获取的新疆CMONOC基准站的水平速度精度较高。修正后基准站E 方向速度平均值为 29.681 mm/a，N 方向速度平均值为8.828 mm/a；N 和E 方向即整体水平方向运动的平均速率为30.966 mm/a，优势方向为NEE73°26′06″。

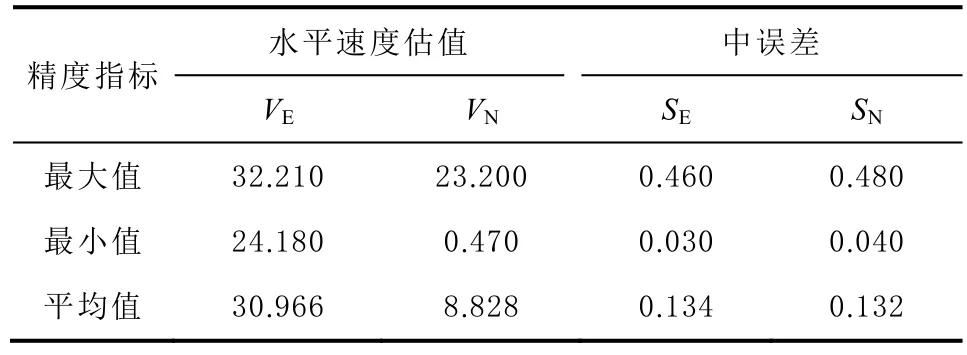
表2 水平速度估值和中误差统计 mm/a

绘制未考虑最优噪声模型改正的ITRF14 框架下新疆CMONOC基准站的垂向运动速度场，结果如图10 所示。

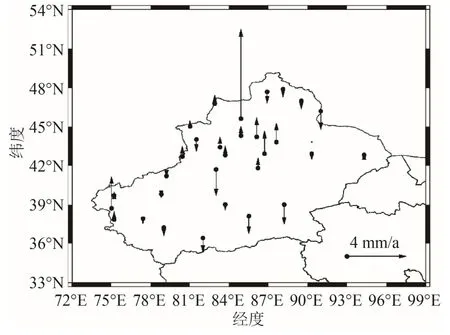
图10 修正前的垂向速度场

从图可以看出，新疆东北部运动方向近似向上运动，而西南部地区为向下运动。未修正新疆陆态网络基准站在ITRF14 框架下垂向运动的平均速率为0.207 mm/a。

表3 给出了未修正的ITRF14 框架下新疆境内CMONOC基准站的竖直方向速度估值和中误差统计结果。

表3 垂向速度估值和中误差统计 mm/a

统计表明，U 方向速度的标准差为1.415 mm，可知本文获取的新疆CMONOC基准站的垂向速度精度较高。由表可见，基准站U 方向速度平均值为0.207 mm/a。

3.2 修正后的速度场模型

绘制经最优噪声模型改正后的ITRF14 框架下新疆CMONOC基准站的水平运动速度场，如图11所示。结果与中国地震局GNSS 数据产品服务平台[14]结果基本一致，即图9 所示。新疆东部运动方向为近E 向，而西南部地区为E—N 向运动。修正后新疆陆态网络基准站在ITRF14 框架下水平方向运动的平均速率为 30.976 mm/a，运动方向为NEE73°23′27″。

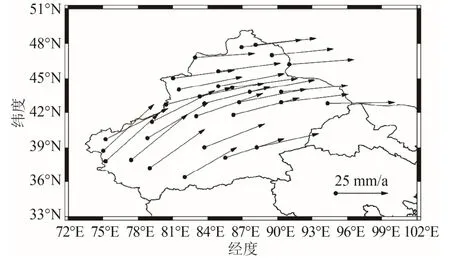
图11 修正后的水平速度场

表4 给出了经最优噪声模型修正后ITRF14 框架下新疆境内CMONOC基准站的水平方向速度估值和中误差统计结果。统计表明，E 方向速度的标准差为2.167 mm，N 方向标准差为6.368 mm，修正后新疆CMONOC基准站的水平速度精度较高，且整体精度优于未经最优噪声模型修正的原始速度场模型。表中可以看出，基准站E 方向速度平均值为29.684 mm/a，N 方向速度平均值为8.854 mm/a。

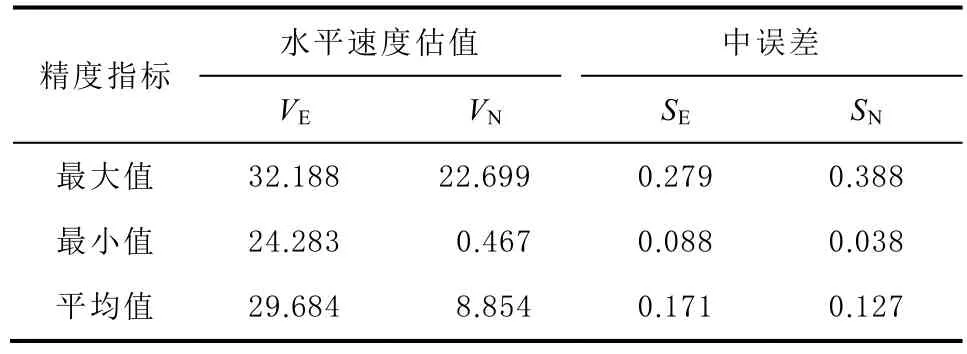
表4 水平速度估值和中误差统计表 mm/a

绘制经最优噪声模型改正后的ITRF14 框架下新疆垂向运动速度场，如图12 所示。结果与中国地震局 GNSS 数据产品服务平台[14]结果基本一致，即如图10 所示。修正后新疆陆态网络基准站在ITRF14 框架下垂向运动的平均速率为0.153 mm/a。

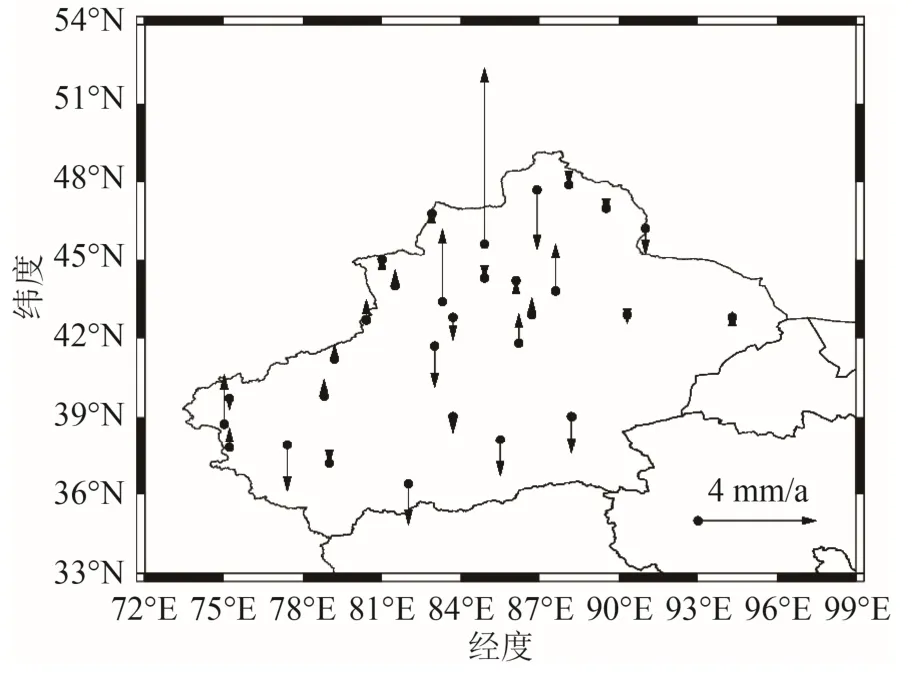
图12 修正后的垂向速度场

表5 给出了经最优噪声模型修正后ITRF14 框架下新疆境内CMONOC基准站的竖直方向速度估值和中误差统计结果。

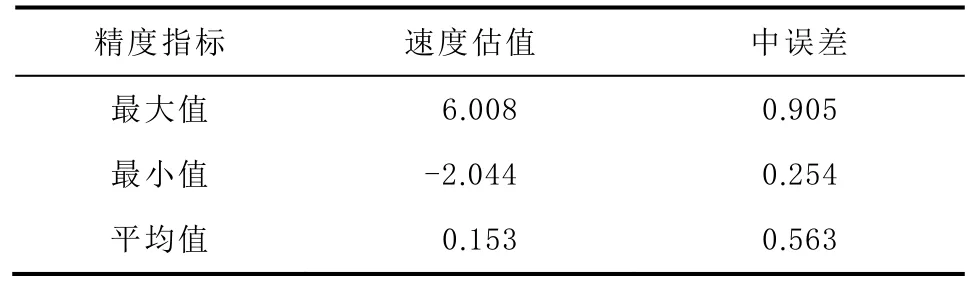
表5 垂向速度估值和中误差统计 mm/a

比较修正前后的标准差：本文获取的新疆CMONOC基准站的垂向速度精度较高，U 方向速度的标准差为1.458 mm；且整体精度优于未经最优噪声模型修正的原始速度场模型。

对比修正前后的速度场模型可知：经最优噪声模型修正后的速度场精度明显优于未修正的速度场，二者在水平方向上的运动速率最大差值为1.394 mm/a；水平运动方向角最大差值可达1°50′59″；垂直方向上的运动速率最大差值为1.730 mm/a。因此，在处理时间序列数据以及解算速度场时，有必要考虑有色噪声的最优模型。

在新疆陆态网络31 个测站中，南北分量以塔什库尔干站（TASH）的速率值最大，为22.699 mm/a，芨芨台子站（XJJJ）的为最小，速率为0.467 mm/a；东西分量以乌拉斯台站（XJWL）为最大，速率为32.188 mm/a，布伦口站（XJBL）为最小，速率为24.283 mm/a；垂向分量以克拉玛依站（XJKL）为最大，速率为6.008 mm/a，木垒站（XJML）为最小，速率为0.004 mm/a。可以看出，东西分量运动速率的最值之间差距为7.905 mm/a，差距并不大。其原因可能是新疆西南地区受印度板块的挤压，使其向N 方向运动速率增大，而阿勒泰及天山东部地区沿N 方向运动速率较小，也就是说从新疆西南部至东北部，在N 方向上的运动速率依次递减，且过渡平稳。总体向E 方向沿顺时针运动，这与文献[4]的研究结果一致。在垂直方向上，可以看出盆山结合部垂直运动速率相对较高且垂直向运动速率差值较大，进而可以推断天山及其周边区域整体呈现隆起的趋势[3]，进一步证明了文献[3]研究结果的可靠性。

4 结束语

本文选取中国地震局GNSS 数据产品服务平台提供的新疆境内31 个CMONOC 连续站10 a的坐标时间序列观测数据，采用贝叶斯信息准则获取了新疆地区各坐标分量对应的最优噪声模型，并确定了修正后的新疆陆态网络速度场。最后得到如下结论：

1）通过10 a的观测数据，得到了较为稳定且可靠的3 个方向分量时间序列与最优噪声模型之间的关系，且N 分量和E、U 分量具有明显不同的噪声特性：在N 方向上，最优噪声模型为组合模型“WN/GGM”；在E 方向和U 方向上，最优噪声模型均为组合模型“WN/FN”。

2）量化了3 个方向分量上最优噪声模型所占百分比：在N 方向上，组合模型“WN/GGM”噪声模型占比70.97%；E 方向上，组合模型“WN/FN”噪声模型占比51.61%；在U 方向上，组合模型“WN/FN”噪声模型占比80.65%。

3）经最优噪声模型修正后的速度场精度明显优于未修正的速度场，二者在水平方向上的运动速率最大差值为1.394 mm/a；水平运动方向角最大差值可达1°50′59″；垂直方向上的运动速率最大差值为1.730 mm/a。因此，在处理新疆时间序列数据以及解算速度场时考虑有色噪声的最优模型是十分必要的。