低成本BDS 双频单点定位方差分量估计方法

徐天扬，章浙涛，何秀凤，陈广鄂

（1.河海大学 地球科学与工程学院，南京 211100；2.同济大学 测绘与地理信息学院，上海 200092）

0 引言

北斗卫星导航系统（BeiDou navigation satellite system,BDS）是中国自主研发、独立运行的全球卫星导航系统（global navigation satellite system,GNSS），是我国对世界的重要贡献。于2012 年建设完成的北斗卫星导航（区域）系统即北斗二号（BeiDou navigation satellite (regional) system,BDS-2），由5 颗地球静止轨道（geostationary Earth orbit,GEO）卫星、5 颗倾斜地球同步轨道（inclined geosynchronous orbits,IGSO）卫星和4 颗中圆地球轨道（medium Earth orbit,MEO）卫星[1]组成。2020 年，第 3 代北斗卫星导航系统即北斗三号（BeiDou navigation satellite system with global coverage,BDS-3）最后1 颗全球组网卫星完成发射，标志着BDS-3 全面建成，整个系统由3 颗GEO 卫星、3 颗IGSO 卫星和24 颗MEO 卫星组成。

北斗卫星导航系统（BeiDou navigation satellite system,BDS）是全星座播发3 频信号的GNSS。BDS-2 播发频率为1 561.098 MHz的B1信号、频率为1 207.140 MHz的B2 信号和频率为1 268.520 MHz的B3 信号。BDS-3 播发B1、B3 信号，不再播发 B2 信号，但新增了频率为1 575.42 MHz的B1C 信号及频率为1 191.795 MHz的B2a 信号；B1C 及B2a 为民用导航信号。与美国的全球定位系统（global positioning system,GPS）只有部分卫星可以播发3 频信号不同，BDS-2、BDS-3的每颗卫星都可以播发3 个频率的信号。BDS的多频信号给用户提供了更多的组合，增加了多余观测量，提高了卫星定位精度的稳定性与可靠性。

目前市场主要分为消费市场的低成本接收机和工程领域的测量型接收机。低成本接收机由于其体积质量小，可以满足小型平台对GNSS 接收机的体积和载荷的限制性要求[2-3]，而且成本低廉，针对的是消费市场的需求。但在测量精度上，低成本接收机不如测量性接收机，单点定位的精度不如测量型接收机的结果，而且可以接收的观测值也更少[3-4]。受到接收机和天线本身的卫星信号处理能力的影响，不同的接收机在信号质量和稳定性上会表现出很大的差异[3,5]。本文探讨基于低成本接收机 Ublox 在静态模式下的单点定位，该低成本接收机可以接收BDS B1、B2 2 个信号的频率，从而可以实现双频单点定位的计算。

如何合理确定多频多模GNSS 组合定位的不同观测值的权，是提高组合系统导航定位精度的关键。当前GNSS 不同观测值组合定位采用的随机模型一般为以下3 种：等权模型、高度角模型[6]、验后估计模型[7]。等权模型形式简单，但该模型把不同的观测值视为等精度，而许多观测值并不等权；因此这种方法不够准确，会造成定位结果的偏差。卫星高度角模型把卫星高度角作为函数的变量来计算各观测值的方差，可有效减小低高度角的差异对定位的影响，是目前普遍采用的定权方法；但是仅考虑了卫星高度角的因素，在含有多种观测值的情况下不够准确。验后估计模型的本质是随机模型的验后估计，其基本思想为先对不同观测量初次定权，再预平差，然后利用预平差后得到的观测值残差阵V对各类观测量值的方差因子和协方差矩阵重新估计。其中，赫尔默特（Helmert）方差分量估计作为一种常用的验后方差方法，被广泛应用于卫星定位领域。文献[8]在GPS 及格洛纳斯卫星导航系统（global navigation satellite system，GLONASS）组合标准单点定位中，通过对这2 个系统进行Helmert 方差分量验后定权，得到此组合定位结果相比于单个系统的点位精度更高的结论。文献[9]通过Helmert 方差分量估计进行系统间的定权，得到GPS 与BDS 间伪距观测值的最优权比为1∶1。文献[10]比较以上3 种模型在BDS/GPS 组合定位中的精度，得到Helmert 方差分量模型定位精度优于卫星高度角模型与等权模型的结论。

以上文献主要是在不同的导航系统的观测值间定权，但是很少基于同一系统不同类型的观测值进行定权。本文从BDS 单个系统的不同频率观测值出发，对单一系统的不同观测值定权。从文献[11]中可得知，尽管双频定位的观测值更多，但是由于双频无电离层组合放大了观测噪声，在电离层延迟较小时的定位精度反倒不如单频单点定位的结果。所以本文对于双频定位采用非组合的方式，并提高不同类型观测的定权精度，以达到提高定位结果精度的目的；然后通过采用低成本接收机Ublox 数据进行实验计算和比较定位结果，比较双频单点定位分别采用卫星高度角定权模型和Helmert 双差分量估计定权模型的定位结果的精度。旨在探讨在低成本接收机多余观测较少的情况下，通过采用方差分量估计定权的方法来提高北斗卫星双频单点定位精度的可行性。

1 双频单点定位模型

1.1 数学模型

BDS B1、B2 信号的伪距观测方程分别为：

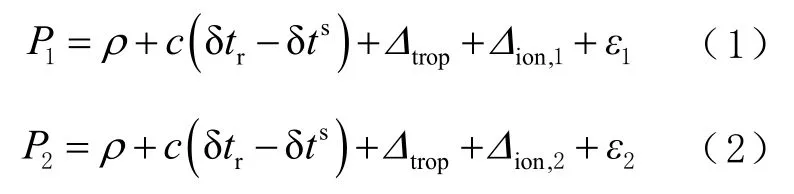
式中：P1、P2分别为B1、B2 信号的观测值；ρ为站星的几何距离；δtr为接收机钟差；δts为卫星钟差；Δtrop为对流层延迟；Δion,1、Δion,2分别为B1、B2 信号的电离层延迟；ε1、ε2为伪距噪声。

对流层采用萨斯塔莫伊宁（Saastamoinen）模型，它是GNSS 定位常用的一种对流层改正模型。对流层的延迟是由干分量延迟与湿分量延迟组成，其常用模型可以表示为

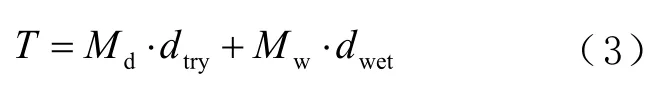
式中：T为对流层总延迟；dtry、dwet分别为天顶干分量与湿分量；Md、Mw为干分量与湿分量分别对应的映射函数。

电离层延迟采用克洛布彻（Klobuchar）模型，它是单点定位中最常用的对电离层延迟的改正模型，该模型将白天的电离层延迟视为随时间变化的余弦函数，而将晚上的电离层延迟视为一个常数。

BDS 广播星历中的卫星钟差的基准是B3 频点，而此次实验的接收机采集到的是BDS 卫星的B1、B2 信号。尽管各种卫星信号都是在同一台原子钟信号的驱动下生成的；但由于不同信号生成的方法不同，所用的电子元器件和电子线路也不同，因此所产生的信号内部时延也是不相同的[12]：所以要对这2 种频率的观测值进行内部时延的修正。

1.2 高度角定权模型

高度角定权随机模型是目前GNSS 定位中最常用的定权模型。对流层延迟误差随着卫星高度角的减小而逐渐增加，卫星高度角高的信号质量通常优于卫星高度角低的信号[13]。高度角定权其实质就是以高度角为指标，对具有不同高度角的观测值进行方差估计而得到的一种简单的验前随机模型，形式简单，计算量小。

由于观测的基线向量以及卫星轨道模型都是基于空间3 维（3D）直角坐标系，所以卫星的高度角和方位角也可以基于笛卡尔运算法则，通过构建直角坐标系统来获得；但目前更常用的是基于矢量的方法求得卫星高度角。

首先将卫星与测站的在空间直角坐标系下的基线向量通过平移旋转，得到站心坐标下的在东、北、天顶3 个方向的坐标E、N、U[14]为：

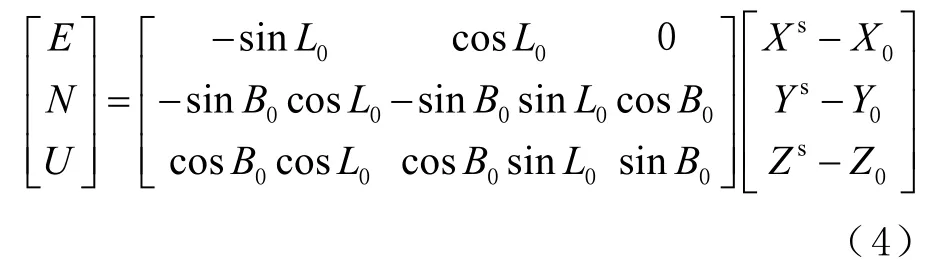
式中：L0、B0分别为测站坐标的经度、纬度；Xs、Ys、Zs为卫星的空间直角坐标；X0、Y0、Z0为测站的空间直角坐标。

则可以求得该卫星与测站间的卫星高度角

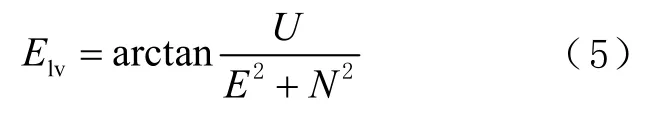
然后就可以利用卫星高度角进行观测值方差的估计。其中一种方法就是利用正弦三角函数公式对不同高度角卫星的观测值方差σ2进行估计，即

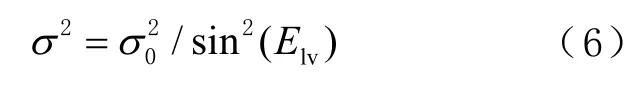
由于BDS 空间星座包括GEO 卫星、MEO 卫星和IGSO 卫星，这些卫星高度差异较大；当卫星高度角相同时，卫星高度可能不一样，仅以卫星高度角定权未必准确[15]。

1.3 Helmert 方差分量估计

Helmert 方差分量估计是一种利用预平差的改正数V，按验后估计各类观测量验前方差的方法。以2 种独立的观测值L1、L2为例，它们的误差方程为

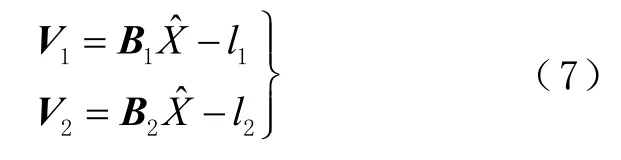
式中：V1、V2分别为L1、L2的改正数；B1、B2分别为L1、L2的系数阵；为参数改正数；l1、l2分别为L1、L2的观测残差。利用最小二乘求得残差，然后依次求得各类残差的平方和由此估计出新的单位权方差，即

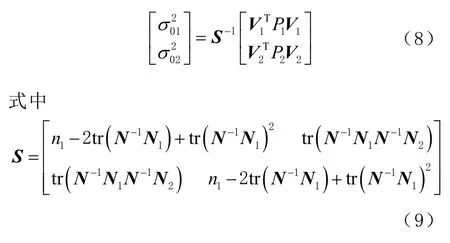
式中：n1、n2分别为L1 与L2 频率的观测值个数；

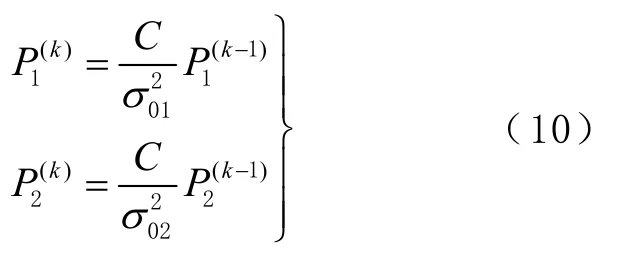
2 实验与结果分析

本实验算例选取了Ublox 接收机1 h 内采集的数据。观测时间为1 h，采样间隔1 s，共3 600 个历元。由于该低成本接收机只能够接收BDS B1、B2 信号，所以读取了BDS 卫星在B1、B2的伪距观测值。通过图1 可以看出在观测时段内卫星数较少，从而观测值数也较少。图2 为卫星在这1 h内运行轨迹的天空图。

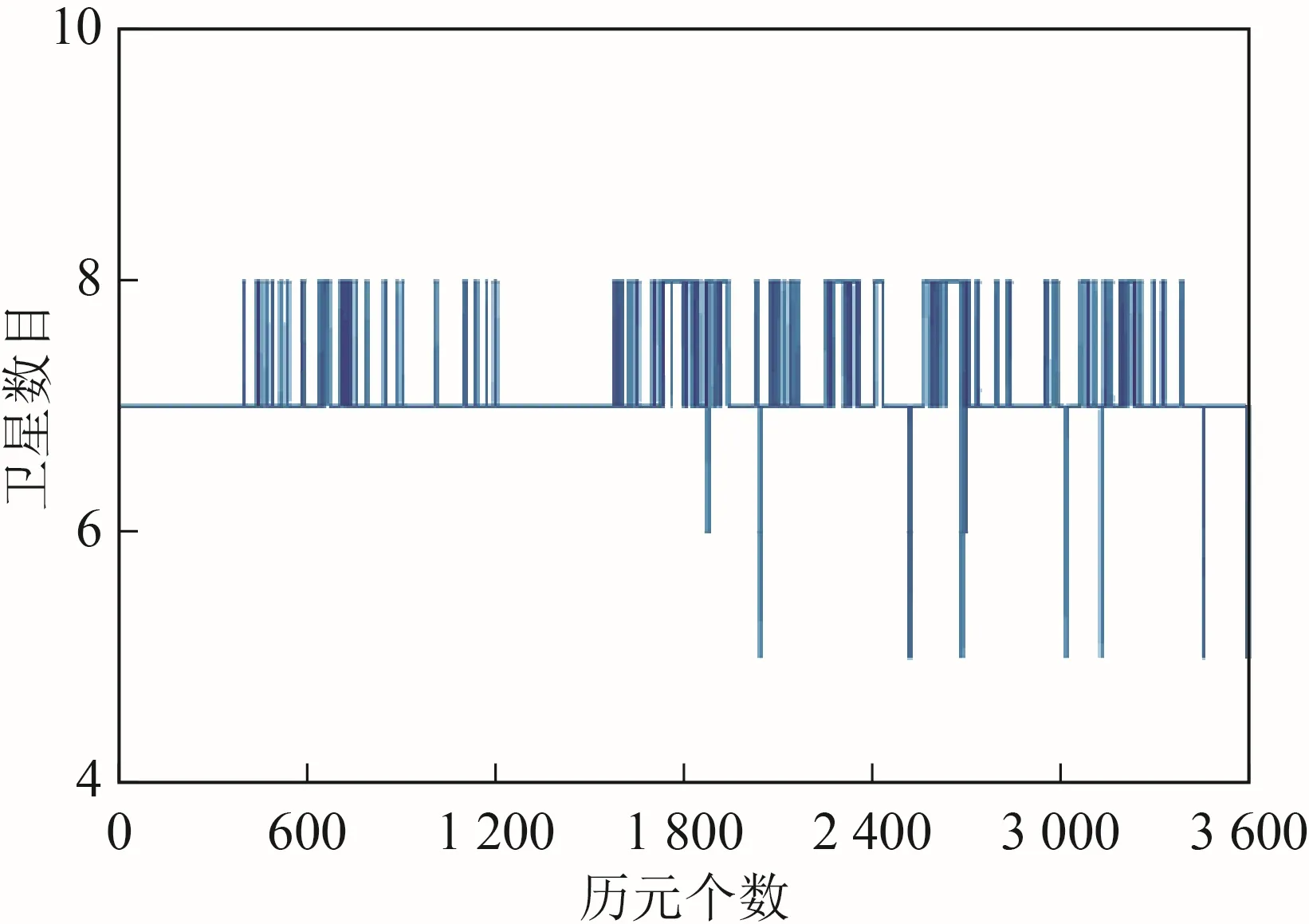
图1 BDS 卫星数

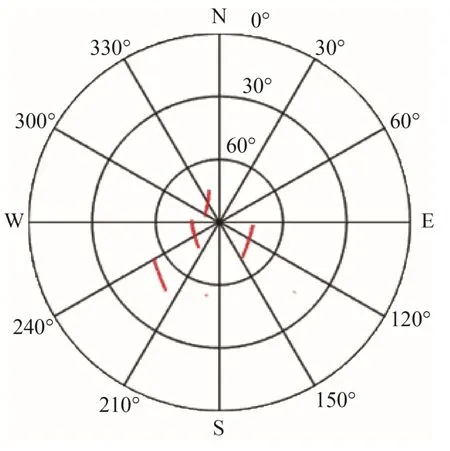
图2 BDS 卫星运行轨迹

本文利用高级程序设计语言C++自行设计的单点定位程序，对卫星钟差、对流层延迟、电离层延迟、地球自转、相对论效应都进行了改正，并设置卫星高度角为 10°。先对卫星先验方差采用卫星高度角定权，其次用最小二乘平差得到观测值残差，再次利用Helmert 方差分量估计重新定权，然后对比仅采用卫星高度角模型的定位结果与后来又采用Helmert 方差分量估计的定位结果。接着利用 RTKLIB 软件的精密单点定位（precise point positioning，PPP）静态模式计算出接收机的坐标。因为其在PPP 静态模式下的精度远高于单点定位的精度，所以可以作为接收机的坐标真值。最后对 2 种定权模式进行比较：①B1/B2 双频定位，采用卫星高度角定权；②B1/B2双频定位，先采用卫星高度角定权，再利用Helmert 方差估计定权。

2.1 定位动态解

图3 为2 种定权模式下在东、北、天顶3 个方向的真误差的结果比较。

从图中可以看出：采用Helmert 方差分量定权得到的各历元的位置结果与B1/B2 采用卫星高度角定权得到的位置的结果相差较大；前者各历元的结果更接近真值且波动变化更小。

表1 为2 种模式下内符合精度标准差（standard deviation，STD）的比较。表2 为2 种模式下外符合精度均方根误差（root mean square error，RMSE）对比。

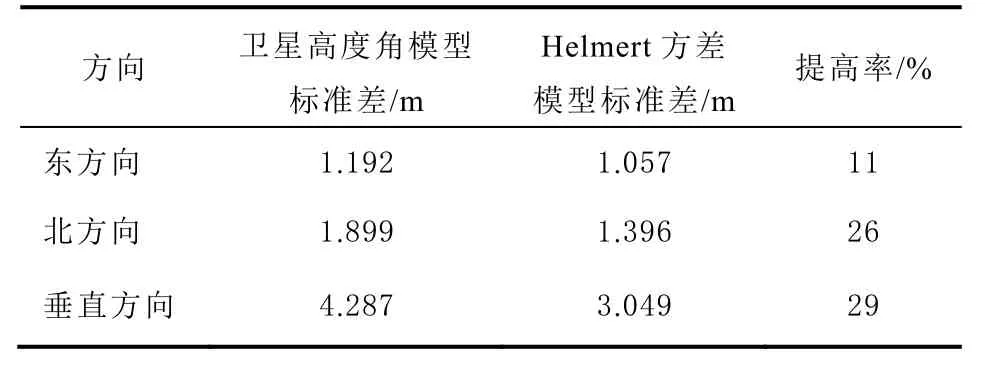
表1 BDS 双频不同随机模型下组合定位的标准差对比

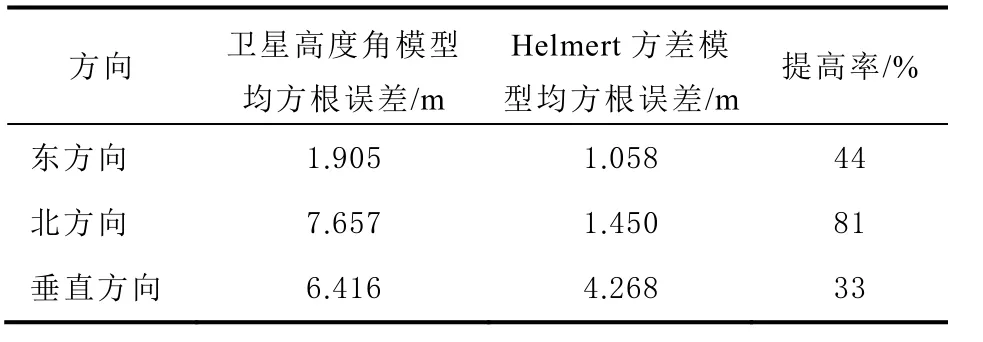
表2 BDS 双频不同随机模型下组合定位的均方根误差对比

从表中可以看出，B1/B2 双频采用Helmert方差分量估计的定权的定位结果无论是内符合精度还是外符合精度，在东、北、天顶3 个方向上都高于B1/B2 双频采用卫星高度角的定权定位结果。

2.2 定位静态解

以上是2 种模式下动态解的精度对比。同样的，可以对多个历元的观测值进行整体解算，通过法方程叠加的方式来比较2 种模式的静态结果。表3 反映了2 种模式得到的静态解与真值在X、Y、Z3 个方向上的偏差。

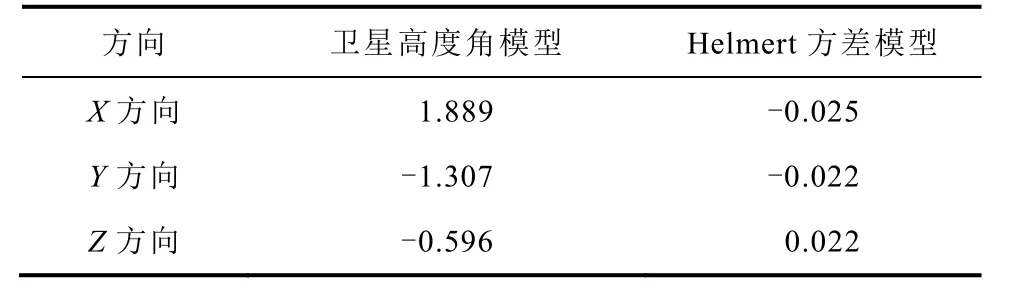
表3 静态定位结果与真值的偏差 m

从表中可以看出，整体解得到的结果要远远好于单个历元的解。相对于仅采用卫星高度角模型的B1/B2 双频定位得到的米级误差结果，采用了Helmert 方差分量估计的B1/B2 双频定位得到的结果误差仅在毫米级，与真值十分接近。所以采用Helmert 方差分量估计模型对于整体解也有一定的提高。

3 结束语

通过对低成本接收机Ublox 所采集的数据进行处理，对比了B1/B2 双频分别采用卫星高度角定权与Helmert 方差分量定权的定位结果，得到以下结论：

1）在双频定位时，如果不能对不同类型的观测值确定合理的权，则定位结果不如单频定位理想；反之，如果能确定不同观测值之间的合理权比，则可以得到更优的定位结果。所以通过Helmert方差分量估计定权对于提升双频定位的精度是有一定帮助的。

2）最常用的卫星高度角模型在双频定位时可能出现失效的情况，而采用Helmert 方差分量估计得到的双频定位结果，无论是动态解还是静态解的精度都有很大的提升，尤其是静态解得到的结果非常接近真值。

3）方差分量估计一般用于多余观测值较多的情况下，可以得到较优的定位结果。而低成本接收机受自身的限制，多余观测值相对较少。本次实验验证了方差分量估计在多余观测数较少的情况下仍有较大的定位优势，在E、N、U 3 个方向上的定位精度都能有较大的提高。