基于整体最小二乘原理的GPS 轨道坐标拟合

谢孟辛，张捍卫，李鹏杰，赵东方

（1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454003；2.河南理工大学 资源与环境学院，河南 焦作 454003）

0 引言

国际全球卫星导航系统（global navigation satellite system,GNSS）服务组织（International GNSS Service,IGS）提供的全球定位系统（global positioning system,GPS）精密星历，其采样间隔为15 min。而实际观测中，GPS 接收机的采样率一般低于1 min。因此，用户须对GPS 精密星历进行数值拟合，才能够获得任意时刻卫星的轨道坐标[1]。

国内外学者对基于GPS 精密星历的卫星轨道逼近方法有很多论述，主要分为插值法和拟合法2 个大类[2]。常用的插值方法为拉格朗日（Lagrange）插值，因其数学模型简单、插值公式易于求得，是最经典最常用的卫星轨道坐标插值方法[3-5]。当用户需要插值较长弧段时，根据拉格朗日插值定理，须将插值多项式展开到较高的阶次；但在此情况下，拉格朗日插值在插值区间端点附近将产生龙格现象，即在插值区间端点附近根据插值函数计算的插值坐标含有较大误差[6]。为解决这个问题，文献[7-8]分别使用滑动插值法和切比雪夫（Chebyushev）多项式插值法：前者鉴于长弧段插值时在插值区间端点将产生龙格现象，而使插值点始终位于插值区间的中心；后者依据切比雪夫多项式定理通过重新选取插值节点使插值误差的最大值最小，借此改善插值区间端点附近卫星轨道坐标计算不准确的问题。目前常用的拟合方法是根据最小二乘原理，以切比雪夫多项式为基函数，对精密星历进行拟合，此拟合方法不会在拟合区间端点附近出现龙格现象，在拟合弧段长度和拟合精度方面也优于拉格朗日多项式插值[9-12]。因此，现在一般多采用切比雪夫多项式最小二乘拟合法对精密星历进行数值拟合。文献[13-14]利用此拟合方法进行具体应用，得到较好的拟合结果。但根据最小二乘原理以切比雪夫多项式为基函数对精密星历进行数值拟合时，随着拟合弧段增长和拟合阶数增加，法方程将变为病态方程[15]，对精密星历拟合函数系数的求解产生极大扰动，导致精密星历拟合结果误差增大且趋于发散，卫星轨道坐标拟合精度降低。

针对目前常用的最小二乘拟合法在高阶次精密星历拟合时拟合误差逐渐增大且趋于发散的问题，本文提出一种更为稳健的拟合方法即整体最小二乘拟合法，并以正交多项式和常规多项式为基函数，分别根据最小二乘原理和整体最小二乘原理对精密星历数据进行拟合。

1 最小二乘拟合

1.1 切比雪夫多项式拟合

在拟合弧段tΔ 内，以n阶切比雪夫多项式为基函数，拟合GPS 卫星精密星历。设t0为拟合弧段的初始历元，由切比雪夫多项式的性质，使用转换公式[11]为

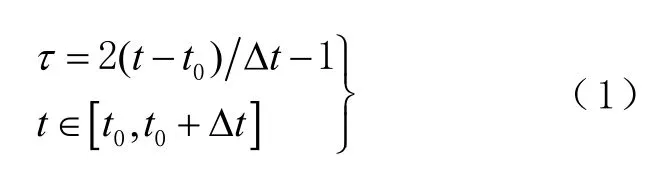
将变量t归化到区间τ∈[− 1,+1 ]上，卫星坐标可用切比雪夫多项式[13]表示为

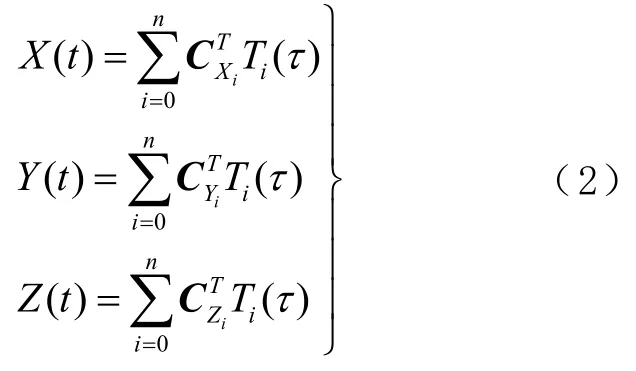
式中：n为切比雪夫多项式的阶数；和分别为卫星X、Y和Z坐标分量的切比雪夫多项式系数，上标T表示切比雪夫多项式拟合系数。切比雪夫多项式Ti递推公式[14]为

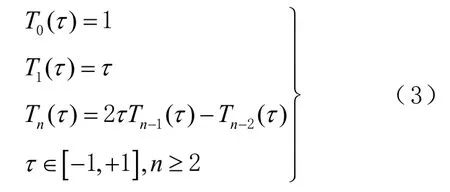
以求解式（2）X坐标分量的切比雪夫多项式系数为例，设xi为观测值，即IGS 提供的GPS精密星历坐标数据，目前在求解最优拟合系数时所列误差方程是在经典的高斯-马尔可夫（Gause-Markov,G-M）模型下建立的，认为只有观测值向量含有误差，误差方程[13]为

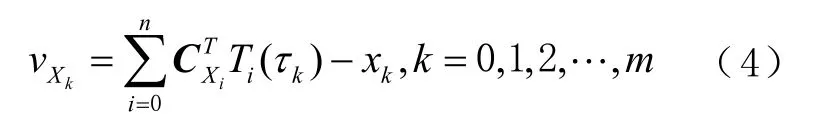
式中：m为拟合过程所用到的精密星历历元个数；为使用切比雪夫多项式拟合法计算的卫星X坐标与观测值xi之差。

将式（4）写成矩阵形式为

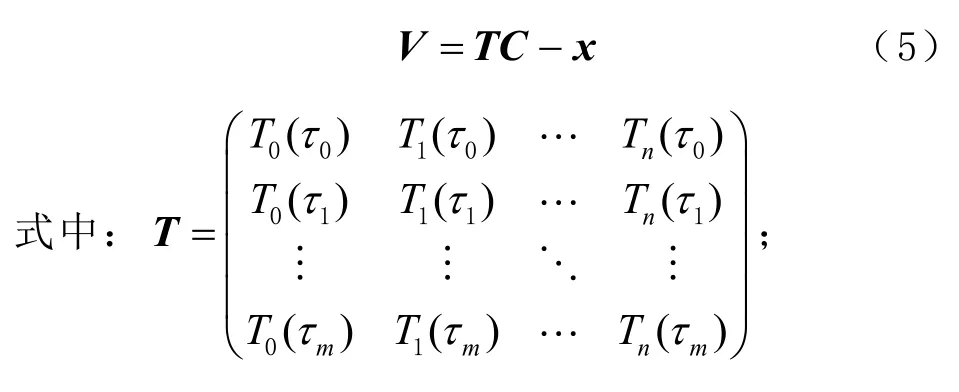
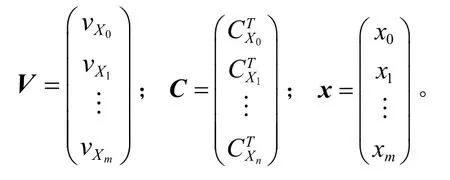
根据最小二乘原理平差准则VTPV=min，由式（5）可得法方程为

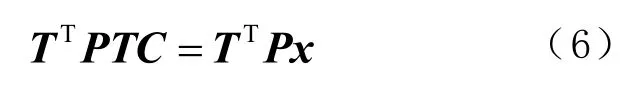
式中P为伪距残差。

由于各卫星轨道观测坐标（精密星历）为等精度观测值，所以P为单位权矩阵，因此有

直接求逆矩阵，解得C为

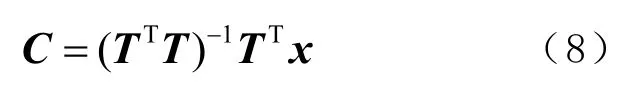
1.2 勒让德尔多项式拟合

与切比雪夫多项式拟合类似，将自变量t归化处理后，卫星轨道坐标的勒让德尔（Legendre）多项式拟合函数为[6]：

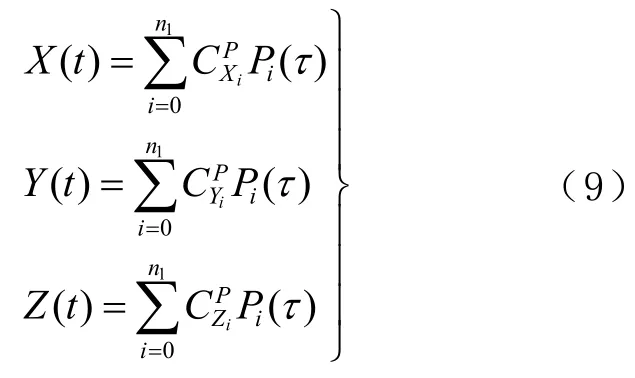
式中：n1为勒让德尔多项式的阶数；和分别为X、Y和Z坐标分量的勒让德尔多项式系数，上标P表示勒让德尔多项式拟合系数。勒让德尔多项式Pi递推公式[16]为

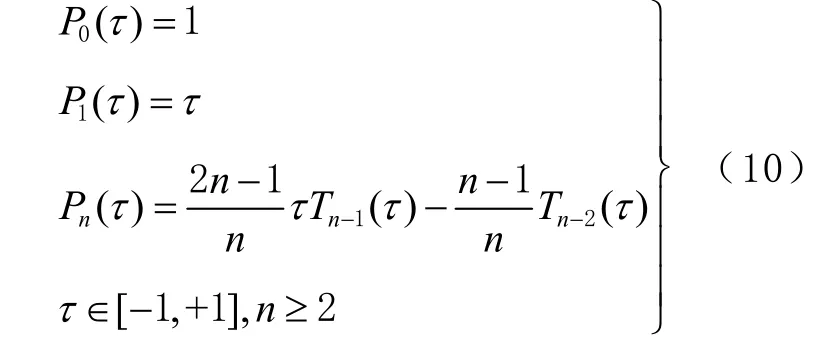
式（9）中多项式系数同样是在G-M 模型下根据最小二乘原理求解，求解算法与切比雪夫多项式拟合法相同。

1.3 常规多项式拟合

卫星轨道坐标拟合时不再使用正交多项式，而使用一组线性无关的常规多项式{t0,t1,…,tn}作为坐标拟合的基函数。为保证数值计算精度，将自变量t正则化处理[1]，即

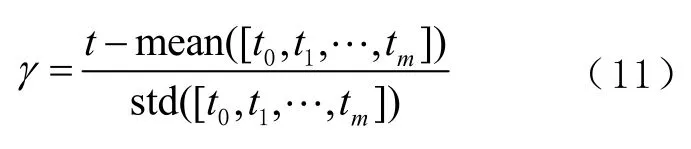
式中 [t0,t1,…,tm]为拟合过程用到的精密星历对应的历元时刻；t∈[t0,t1,…,tm]；mean（）与std（）分别表示求均值和标准差。

卫星轨道坐标的常规多项式拟合函数为

式中：n2为常规多项式的阶数；和分别为X、Y和Z坐标分量的常规多项式系数，上标Y表示常规多项式拟合系数。式（12）中常规多项式系数求解过程与切比雪夫多项式拟合法和勒让德尔多项式拟合法相同。

2 整体最小二乘拟合

上述依据最小二乘原理的切比雪夫多项式拟合法、勒让德尔多项式拟合法和常规多项式拟合法求解的卫星轨道坐标拟合函数都是在经典的GM 模型下根据最小二乘原理求解而得；然而在实际情况中，更多的是观测值向量x和系数矩阵T均存在误差，G-M 模型是不适用的。由式（8）求得的拟合系数C并不是最优无偏的，此时引入变量含误差模型（errors-in-variables,EIV），此模型将观测值向量与系数矩阵的误差均引入误差方程[17]。这里以切比雪夫多项式拟合的误差方程为例进行说明，即可得

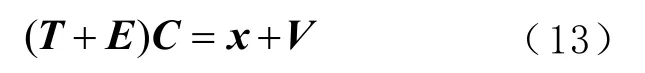
式中E为系数矩阵T的误差矩阵，维数与T相同。将式（13）化为为

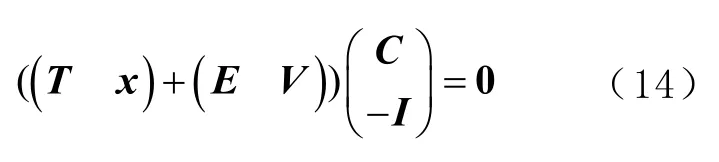
式中I为单位向量。设B=(T x)，D=(EV)，Z=(C−I)T，误差方程式（13）可简写为

在变量含误差模型（EIV）下，使用普通最小二乘法已无法解决问题，需根据整体最小二乘原理求解最优拟合系数C。

本文使用奇异值分解（singular value decomposition,SVD）算法求解整体最小二乘问题，SVD 算法的平差准则为

依据平差准则式（16），文献[18]导出的整体最小二乘SVD 算法如下：

1）对B进行SVD 分解，即

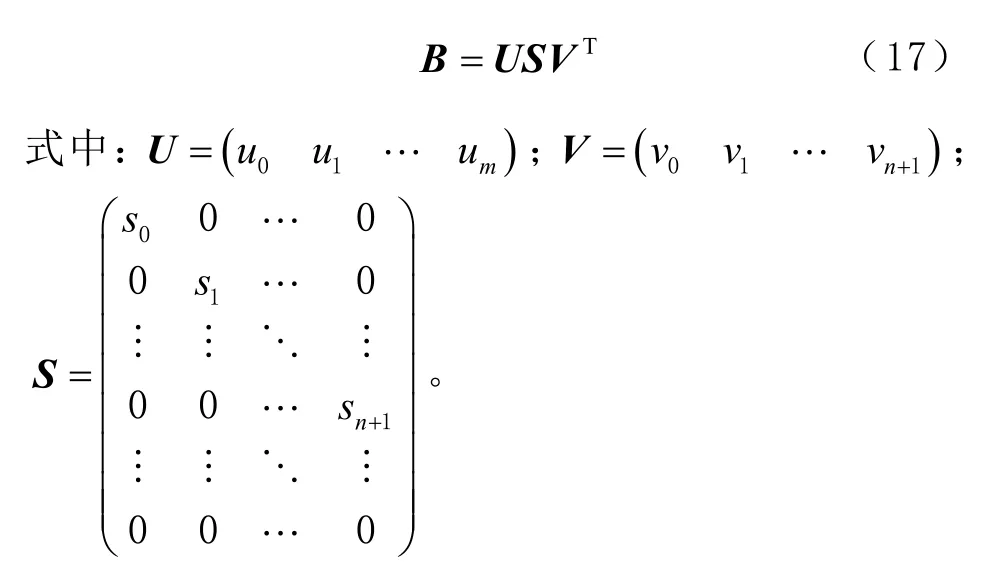
其中：U为（m+1）×（m+1）维正交矩阵；V为（n+2）×（n+2）维正交矩阵；ui和vi为各自正交矩阵内部两两正交的单位向量；S为（m+1）×（n+2）维对角矩阵；si为矩阵B的奇异值（且s0≥s1≥ …≥sn+1≥0）。矩阵U、S和V的维数是通过矩阵B的维数确定的。

2）拟合系数C的整体最小二乘解（s n>sn+1）为

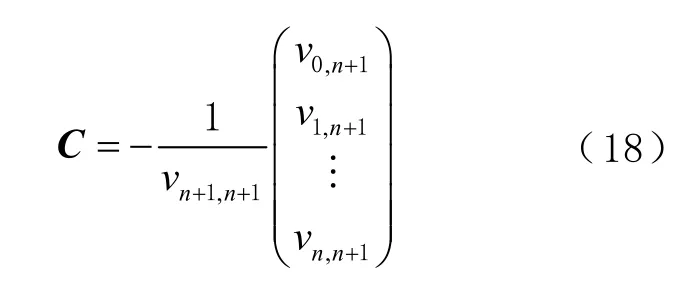
式中vi,n+1表示矩阵V第n+1 列第i个元素。文献[18-19]已进行严密的数学推导，并证明上述奇异值分解算法求解的拟合系数C在EIV 模型下是最优无偏的。

同理，整体最小二乘法的勒让德尔多项式与常规多项式拟合也依照上述奇异值分解算法进行解算。

通过第1 节与第2 节中叙述的拟合算法均可求得卫星轨道坐标拟合函数，即可求出拟合弧段[t0,t0+Δt]内任意时刻的卫星坐标。

3 实验与结果分析

为分析上述各种拟合方法的卫星轨道坐标拟合结果，本文使用IGS 提供的2019-10-05的精密星历数据进行实验分析。实验中GPS 卫星轨道拟合弧段为6 和12 h，采样间隔为15 min，拟合弧段初始时刻为2019-10-05 T 00:00:00。将以上拟合算法拟合结果的中误差列于表1、表2 和图1～图3中，其中mx、my、mz和mp分别为GPS 卫星X、Y和Z坐标分量拟合中误差和点位中误差，单位为mm，其计算公式为

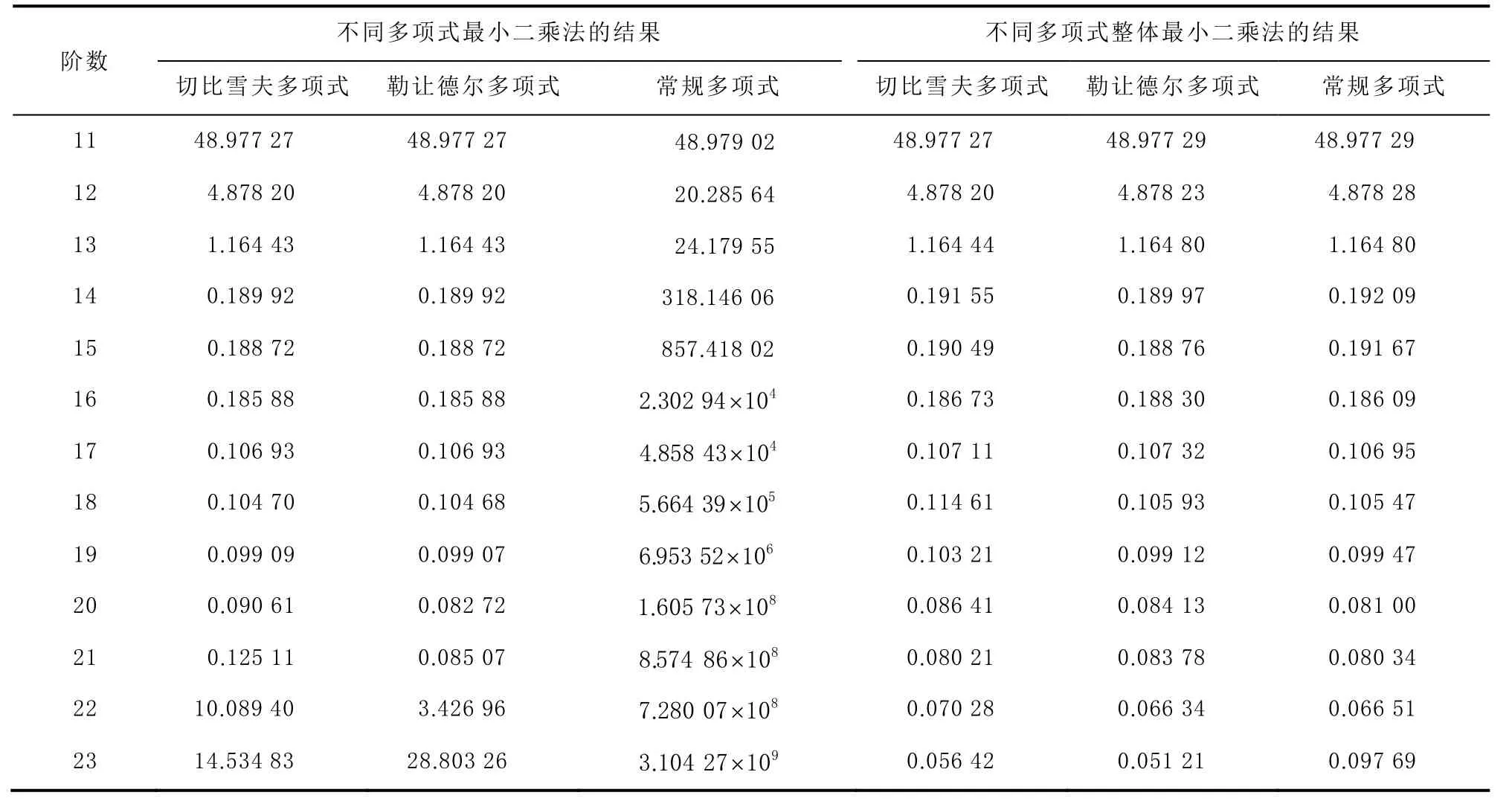
表1 X 方向拟合中误差m x（拟合弧段为6 h） mm

表2 点位中误差mp（拟合弧段为6 h） mm

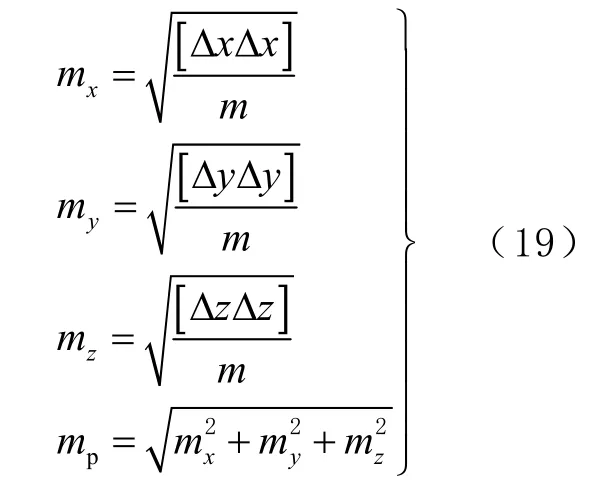
式中：Δx、Δy和Δz为拟合的结果与对应时刻IGS提供的精密星历之间的差值；m为拟合过程中所用到的历元数。在卫星轨道坐标拟合实验中，相同弧段同一算法拟合结果的中误差mx、m y、m z和mp呈现出相同规律。由于篇幅限制，这里只列出mx和mp的结果。

从表中可看出：拟合弧段为6 h，根据最小二乘原理以切比雪夫多项式和勒让德尔多项式（正交多项式）为基函数拟合精密星历时，在拟合阶数小于等于20的区间内，X坐标分量拟合中误差mx与点位中误差mp随拟合阶数的增加而减小，拟合误差在20 阶时达到最小；切比雪夫多项式拟合的X坐标分量拟合的中误差为0.090 61 mm，点位中误差为0.219 35 mm，勒让德尔多项式拟合的X坐标分量拟合的中误差为0.082 72 mm，点位中误差为0.215 81 mm。在拟合阶数大于20 至最大拟合阶数范围，拟合中误差随着拟合阶数的增加而增大，轨道坐标拟合精度降低。拟合弧段为6 h，根据最小二乘原理以常规多项式为基函数拟合精密星历时，在拟合阶数小于等于12的区间内，X坐标分量拟合中误差mx与点位中误差mp随拟合阶数的增加而减小，轨道坐标拟合精度在拟合阶数为12 阶时达到最高；X坐标分量拟合中误差为20.285 64 mm，点位中误差为23.664 46 mm。当拟合阶数大于12 阶时，随着拟合阶数的增加，轨道拟合中误差急剧增大，趋于发散。

卫星轨道拟合弧段为6 h，根据最小二乘原理使用切比雪夫多项式、勒让德尔多项式（正交多项式）和常规多项式进行轨道坐标拟合时，3 种拟合方法拟合结果的X方向的中误差mx和点位中误差mp的数值变化规律相似：在一定阶数范围内，随着拟合阶数的增加，拟合结果的中误差减小，轨道拟合精度升高；拟合阶数超过此区间，随着拟合阶数增加，拟合结果的中误差增大且趋于发散，轨道拟合精度降低。不同之处在于：相比于常规多项式拟合，正交多项式拟合在更高阶次才出现误差发散现象，轨道拟合结果较稳定，且使用正交多项式进行轨道坐标拟合的精度要优于常规多项式拟合。

拟合弧段为6 h，根据整体最小二乘原理以切比雪夫多项式、勒让德尔多项式和常规多项式为基函数拟合精密星历，在所能达到的最高拟合阶数范围内，拟合精度随着拟合阶数的增加而升高，在高阶次拟合时能够保证拟合结果的稳定性，不会出现最小二乘拟合在高阶次拟合时轨道拟合误差增大并趋于发散的现象。并且根据整体最小二乘原理得到的拟合结果精度更高，特别是以常规多项式为基函数根据整体最小二乘原理进行轨道坐标拟合时，拟合结果精度得到了极大的改善。

如图1 与图2 所示，拟合弧段为12 h，根据最小二乘原理和整体最小二乘原理，以切比雪夫多项式和勒让德尔多项式（正交多项式）为基函数进行卫星轨道坐标拟合，其拟合结果与6 h 拟合弧段拟合结果的精度变化规律类似：拟合弧段为12 h，根据最小二乘原理进行轨道拟合时，2 种正交多项式拟合结果在一定阶数范围内，随着拟合阶数的增加，拟合结果的中误差减小，轨道拟合精度升高；拟合阶数超过此区间，随着拟合阶数的增加，拟合结果的中误差增大且趋于发散，拟合精度降低；根据整体最小二乘原理进行轨道坐标拟合，2 种正交多项式拟合在所能达到的最高拟合阶数范围内，拟合精度随着拟合阶数的增加而升高，在高阶次拟合时能够保证拟合结果的稳定性。

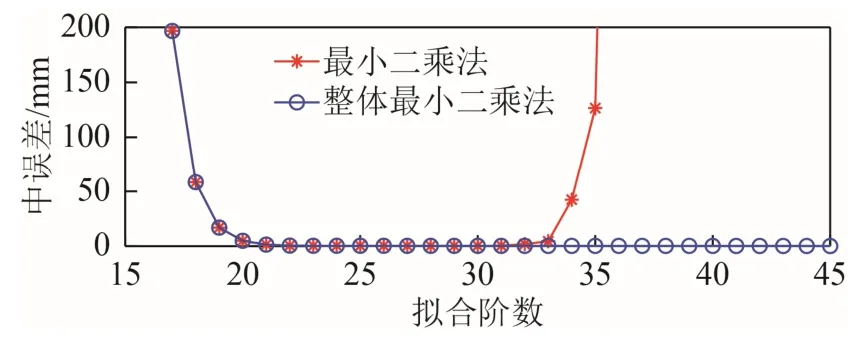
图1 以切比雪夫多项式为基函数的拟合点位中误差mp变化曲线（拟合弧段12 h）

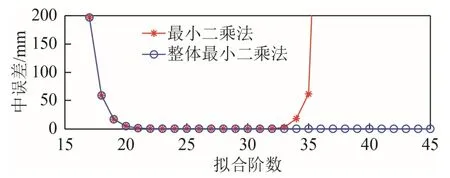
图2 以勒让德尔多项式为基函数的拟合点位中误差mp变化曲线（拟合弧段12 h）

拟合弧段为12 h，根据最小二乘原理以常规多项式为基函数进行轨道坐标拟合，所能达到的最高拟合精度只有米级，如拟合阶数为15 阶时，拟合结果的点位中误差mp最小，为2 548.578 48 mm；拟合阶数大于15，拟合结果中误差随着拟合阶数的增加而急剧增大且趋于发散。即使根据整体最小二乘原理，其在高阶次轨道坐标拟合时也无法保证拟合结果的稳定性，轨道坐标拟合中误差在高阶次拟合时增大且趋于发散，拟合结果精度降低，如图3 所示。

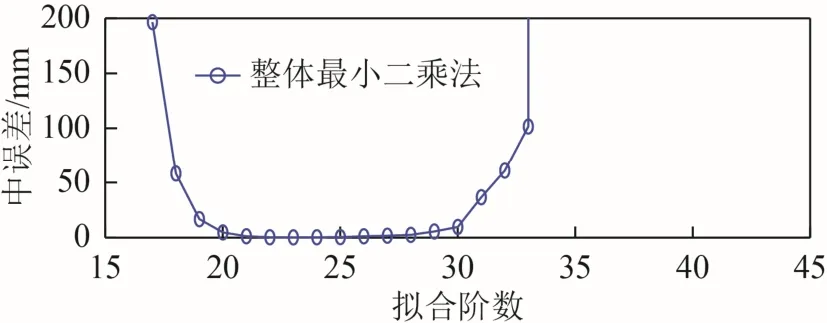
图3 以常规多项式为基函数的拟合点位中误差mp变化曲线（拟合弧段12 h）

综上所述，相比于最小二乘拟合，整体最小二乘拟合的轨道拟合精度更高，在高阶次轨道拟合时拟合结果更稳定，其原因在于：在轨道拟合过程中，求解拟合函数系数C时会遇到病态方程求解问题，特别是最小二乘拟合；随着拟合弧段增长，拟合阶数增加，法方程式（7）TTTC=TTx系数矩阵TTT（PTP,YTY）的条件数（通常以条件数衡量矩阵的病态性）会急剧增加。如表3 与表4 所示。

表中：cond（TTT）、cond（PTP）和cond（YTY）分别表示切比雪夫多项式拟合、勒让德尔多项式拟合和常规多项式拟合的法方程系数矩阵的条件数；cond（T）、cond（P）和cond（Y）分别表示切比雪夫多项式拟合、勒让德尔多项式拟合和常规多项式拟合的误差方程系数矩阵的条件数。法方程式（7）将变为严重的病态方程，求解病态法方程而得到的拟合函数系数C含有极大的误差。针对解决病态方程求解不准确的问题，整体最小二乘拟合有2 个方面的优势：①整体最小二乘拟合无须通过法方程而解得拟合系数C，其是对矩阵T的增广矩阵(T x)进行SVD 分解，由分解而得右奇异矩阵V的元素求解拟合系数C，在此可只考虑矩阵T的病态性，由表3 与表4 可以看出，矩阵T比矩阵TTT的条件数数量级小得多，即使在高阶次拟合时方程仍为良态方程；②整体最小二乘拟合是在EIV 模型下求解拟合函数系数C，计算时将观测值向量误差与系数矩阵误差均纳入误差方程，依据平差准则式（16），使误差方程中系数矩阵误差与观测值向量误差最小，由此可使病态误差方程中系数矩阵误差与观测值向量误差对拟合系数C的求解影响降至最小，而最小二乘拟合只考虑观测值含有误差。

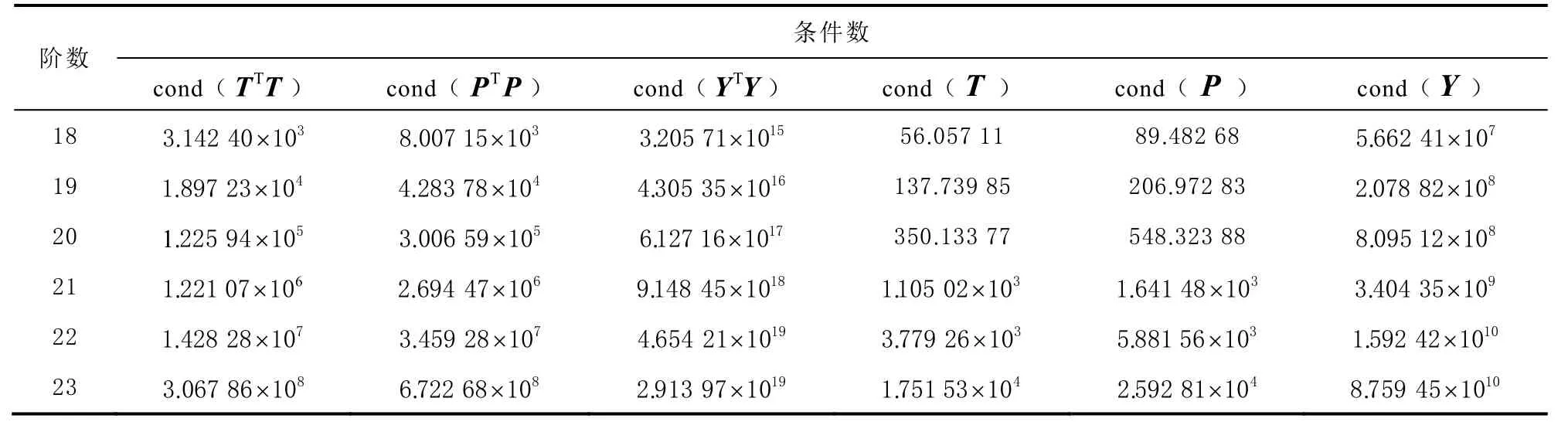
表3 法方程与误差方程系数矩阵条件数（拟合弧段为6 h）

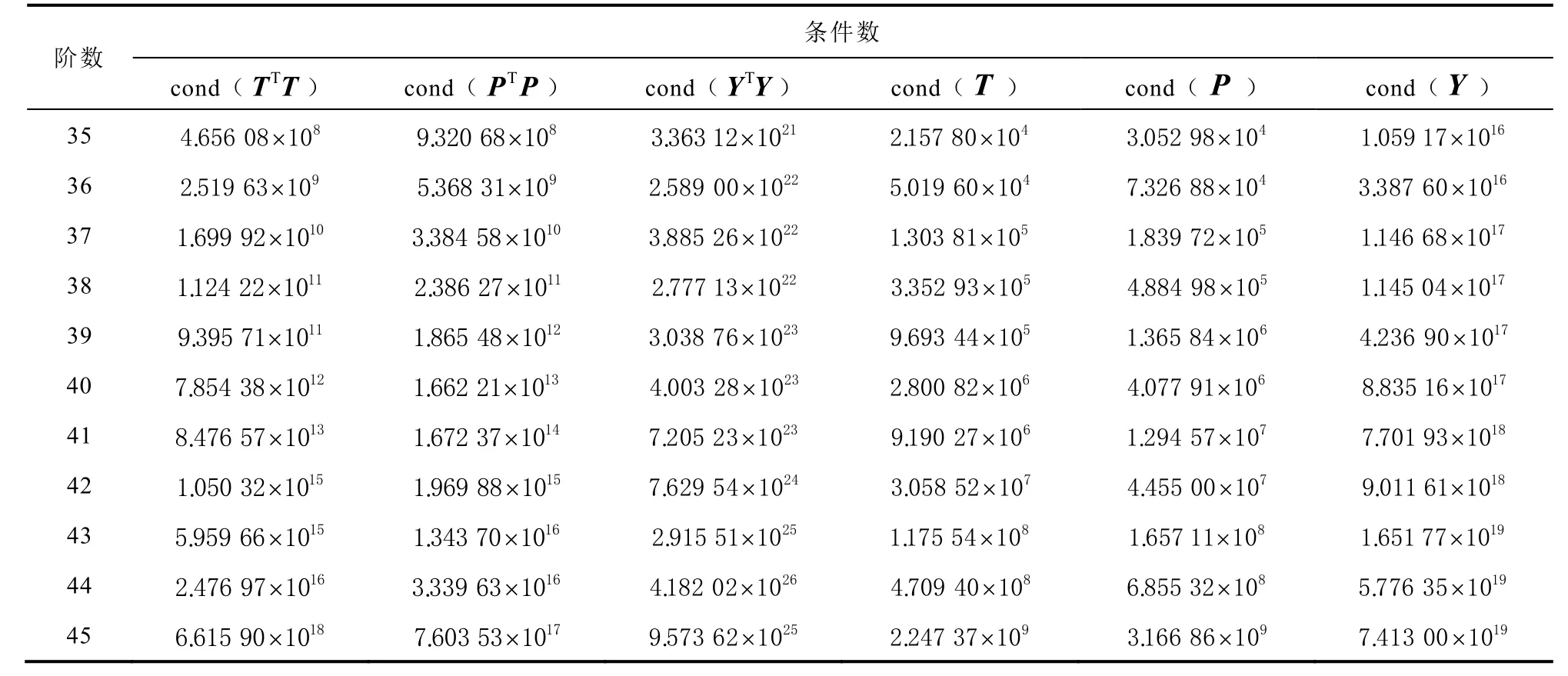
表4 法方程与误差方程系数矩阵条件数（拟合弧段为12 h）

但整体最小二乘法也无法解决条件数极大的病态方程求解的问题。当轨道拟合弧段为12 h 时，对于常规多项式的整体最小二乘拟合，其在高阶次轨道坐标拟合时方程系数矩阵Y的条件数数量级达到1016以上，如表4 所示，此时根据整体最小二乘原理求得的拟合系数C含有较大的误差，卫星轨道坐标拟合结果的误差在高阶次增大且趋于发散，拟合精度降低。正交多项式（切比雪夫多项式、勒让德尔多项式）无论在最小二乘原理还是在整体最小二乘原理下进行轨道坐标拟合，其系数矩阵条件数的数量级明显小于常规多项式系数矩阵条件数的数量级，因此其轨道拟合精度与高阶次拟合时拟合结果的稳定性要优于常规多项式，这正是目前多采用切比雪夫等正交多项式进行轨道坐标拟合的原因。

4 结束语

本文分别基于最小二乘原理和整体最小二乘原理，以正交多项式和常规多项式为基函数，对6 和12 h 弧段的GPS 精密星历进行拟合，并对拟合结果精度进行分析。结果表明：

1）整体最小二乘拟合解决了最小二乘拟合在高阶次精密星历拟合时拟合误差逐渐增大且趋于发散的问题，在拟合结果的稳定性和拟合精度方面均优于最小二乘拟合；

2）在拟合基函数选择方面，鉴于正交多项式（切比雪夫多项式、勒让德尔多项式）在拟合过程的矩阵计算中具有更小的条件数，以正交多项式为基函数进行拟合，拟合结果的稳定性和拟合精度更高。