模糊分数阶滑模控制在PMSM伺服系统中研究与应用

金 鹏

（辽宁工程职业学院电气工程系，辽宁 铁岭 112008）

1 引言

永磁同步电机（PMSM）具有动态响应速度快、功率系数大、负载能力强、节能高效等优点，广泛应用于工业伺服控制领域［1］。因其复杂的电气特性，PMSM伺服系统是一个多变量、非线性、强耦合、时变的系统［1］，难以建立精确模型。一些学者提出PID参数自适应调节的混合算法［2］，如：模糊PID，利用遗传算法调节PID参数，利用粒子群算法调节PID参数等。这些算法可以自适应调节PID参数，并且鲁棒性较好，但前提还是要建立PMSM的精确模型［3-6］。

滑模控制算法（SMC）具有调节参数少、鲁棒性强、无需精确控制模型等优点，近年来在复杂伺服控制系统得到广泛应用［1］。但滑模控制最大的缺点就是系统的执行机构因切换开关在时间及空间存在一定的滞后性，导致滑模动态不能在滑模面准确发生，引起系统抖振。强烈的系统抖振会引起系统耗能过快，激发未建模型的危害［3］。为削弱输出抖振，一些学者提出优化算法，如Terminal滑模控制、状态观测器方法、高阶滑模控制等。但这些算法都存在着各种不足，如Terminal滑模控制必须参数精确，否则容易出现奇异问题［4］；状态观测器在减弱抖振的同时，也降低了系统的鲁棒性，系统稳态误差较大［4-5］；高阶滑模控制器的设计较为复杂，不便于推广应用［6-7］。

分数阶系统具有能量传递缓慢及逐渐收敛的特点［8］，为减弱滑模控制的抖振幅度及频率，降低系统的能量损耗，本文在滑膜控制器的设计中加入分数阶理论。设计一种分数阶滑模控制器，并利用模糊控制算法在线自适应调节滑模切换项ε和分数阶微积分阶次λ。仿真和实验的结果都表明模糊分数阶滑模控制可以有效减弱系统的抖振，缩短调节时间，并具有很强的鲁棒性。

2 PMSM数学模型

这里研究矢量控制方法对PMSM电机转速进行控制。在忽略磁路饱和、空间谐波、涡流及磁滞损耗情况下，电机定子绕组三相对称，气隙磁场正弦分布［1］。在以上前提下，建立d-q坐标下的数学模型。

定子电压方程为：

式中：U d、U q—d、q坐标下的定子电压；L d、L q—d、q坐标下的定子电感；i d、i q—d、q坐标下的定子电流；R s—定子电阻；ωe—电机电角度；ψf—永磁体励磁磁链。

电磁转矩方程为：

式中：p—转子极对数。

机械运动方程为：

式中：T e—电磁转矩；T L—负载转矩；B—摩擦系数；ω—转子机械角速度，且ωe=pω。

由式（3）、式（4）得PMSM机械运动方程：

考虑参数摄动的情况下，式（5）可得：

式中：Δa、Δb、Δc—a、b、c的变化量。

d-q坐标下，PMSM矢量控制系统结构图，如图1所示。系统采用双闭环控制系统，电流环采用PI控制器，速度环采用分数阶滑模控制器，为这里的研究重点。

图1 PMSM矢量控制系统结构图Fig.1 Vector Control System Diagram of PMSM

3 分数阶滑模控制器

定义转速偏差为e(t)，即：

对式（7）求导，并代入式（6）可得：

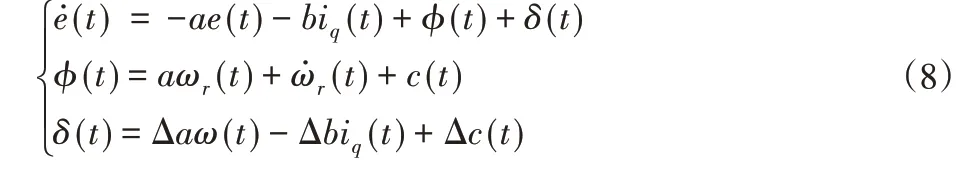
其中，摄动总量δ(t)满足：

选取切换函数为分数阶S函数：

式中：k—滑模面增益；且k>0；—分数阶微积分算子，其定义

如下：

式中：λ—分数阶微积分阶次；R(λ)—λ的实部。

根据式（8）、式（10），并加入开关增益ε和分数阶符号函数，设计分数阶滑模控制器控制率为：

式中：ε—开关增益，且ε>0。ε可以使系统在有限时间内到达滑模状态S=0，但会产生系统抖振；0D-λ tsgn(S)—分数阶符号函数，起到开关切换作用；sgn(S)—整数阶符号函数，定义如下：

图2 符号函数的整数阶与分数阶对比Fig.2 Comparison of sgn(S)and

由式（12）可看出，滑模控制器加入分数阶符号函数，不仅起到弱化系统抖振的作用，由于增加一个调节参数λ，也使得系统的控制精度和灵活性更高。

4 分数阶滑模控制器稳定性分析

所设计的滑模控制器的成立条件是满足［8］：（1）滑模到达条件，即系统可从任意状态到达滑模状态；（2）滑模存在条件，即系统存在滑模状态，使S=0。

（1）滑模到达条件：

选取Lyapunov函数验证所设计控制器稳定性［8-9］：

根据Lyapunov稳定性理论，当̇≤0时，系统满足滑模到达条件［8］。对式（14）等式两端求导，并将式（8）、式（12）带入可得：

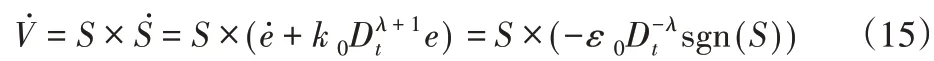
由式（13）可知：S×sgn(S)≥0

所设计的控制器满足全局滑模到达条件。

（2）滑模存在条件：

当系统进入滑模状态，满足S=0，即：

当k>0时：

|arg(-k)|=π>0.5λπ

根据分数阶系统稳定性理论［9-10］，微分方程（16）有解，系统渐进收敛于0。因此，所设计的分数阶滑模控制器满足滑模存在条件。

5 控制器参数整定

由前文可知，要减弱系统抖振需要设置合理的ε和λ。但通过多次实验发现：ε和λ对系统的影响是非线性的。ε影响系统到达滑模状态的时间。加大ε时，系统到达滑状态时间变短，但抖振增强；减小ε时，系统抖振减弱，但系统到达滑模状态时间变长。λ影响系统的抖振强度。系统随着阶次λ的增加，抖振变强；系统随着阶次的减小，抖振变弱，但λ减小到一定值后抖振又变强。因此，如果将ε和λ设为固定值，不能很好地适应PMSM系统的非线性、实时性。本文利用模糊算法自适应调节参数ε、λ的变化量Δε、Δλ。定义ε和λ的初始值设为ε0、λ0，则调节后参数为ε0+Δε、λ0+Δλ。

（1）参数ε整定

本文以S×Ṡ作为模糊控制器的输入，开关增益的变化量Δε作为模糊控制器的输出。定义模糊输入输出的模糊语言变量为：S×̇=Δε={NB，NM，ZO，PM，PB}，代表{负大，负中，零，正中，正大}。模糊控制规则如表1，S×̇隶属度函数，如图3所示。Δε隶属度函数，如图4所示。

图3 S×Ṡ隶属度函数Fig.3 Membership Function of S×Ṡ

图4 Δε隶属度函数Fig.4 Membership Function ofΔε

从表1看出，当S×̇>0时，开关增益ε增大，使系统快速向状态运动；当S×Ṡ<0时，开关增益ε减小，减小系统抖振，使系统逐渐稳定于滑模状态。

表1 模糊控制规则表Tab.1 Fuzzy control rules

（2）参数λ整定

文献［6］设计一种模糊控制器，以转速偏差e为模糊控制器输入，以λ为模糊控制器输出。其模糊控制器设计合理，取得良好控制效果，系统可快速达到稳态，鲁棒性良好。但当系统接近及到达滑模面时，e只能反映系统的抖振大小，不能反映抖振变化趋势。

这里设计一种模糊控制器：以转速偏差e和转速偏差变化率ė为模糊控制器的输入，以分数阶阶次的变化量Δλ为模糊控制器的输出。模糊输入的模糊语言变量为：e=ė=｛NB，NM，NS，ZO，PS，PM，PB｝，代表{负大，负中，负小，零，正小，正中，正大}。模糊输出的模糊语言变量为：Δλ={NB，NM，ZO，PM，PB}，代表{负大，负中，零，正中，正大}。模糊控制规则如表2，e(t)、ė(t)、Δλ隶属度函数，如图5～图6所示。

图5 e、ė隶属度函数Fig.5 Membership Function of e and ė

图6 Δλ隶属度函数Fig.6 Membership Function ofΔλ

从表2看出，当e×ė正大时，系统抖振最强，此时，减小λ，抑制系统抖振；当e×ė负大时，系统抖振减弱的速度最快，系统以最快速度向滑模状态运动，λ维持不变；当e×ė=0时，系统稳定在滑模状态，此时，λ维持不变。

表2 模糊控制规则表Tab.2 Fuzzy Control Rules

6 仿真及实验

6.1 仿真分析

为验证本文所设计模糊分数阶滑模控制器的有效性，分别将本文方法与滑模控制器（SMC）、分数阶滑模控制器（FOSMC）做性能对比。在MATLAB仿真平台上对3种算法进行仿真。设定仿真步长T s=10ms，目标转速ωr=1000r∕min。电机参数如下：P N=1kW，U N=240V，R s=1.5Ω，L d=L q=4e-3H，n p=4，J=1.85e-3kg⋅m2，B m=1.0e-3N⋅ms。仿真实验分别从PMSM系统抖振性、鲁棒性两方面分析对比。

6.1.1 抖振性对比

当目标转速信号为阶跃信号step=1000，3种滑模控制器切换函数S曲线，如图7所示。控制输出，如图8所示。

图7 切换函数S曲线Fig.7 Switching Function Curves

通过图7的S曲线对比看出：当系统到达滑模状态后，本文方法的系统抖振频率和抖振幅度最小；分数阶滑模控制器的抖振幅度和抖振频率要低于整数阶滑模控制器。图8的控制输出对比也体现出相同的结论：当系统进入稳态后，本文方法的控制输出最稳定，PMSM系统的抖振频率和抖振幅度最小。

图8 控制输出Fig.8 Controllers Output

（2）鲁棒性对比

当目标转速信号为阶跃信号step=1000，在t=0.25s时突加大小为0.5N⋅m的干扰负载。3种滑模控制器的电机转速对比，如图9所示。转矩对比，如图10所示。

图9 电机转速Fig.9 Motors Speed

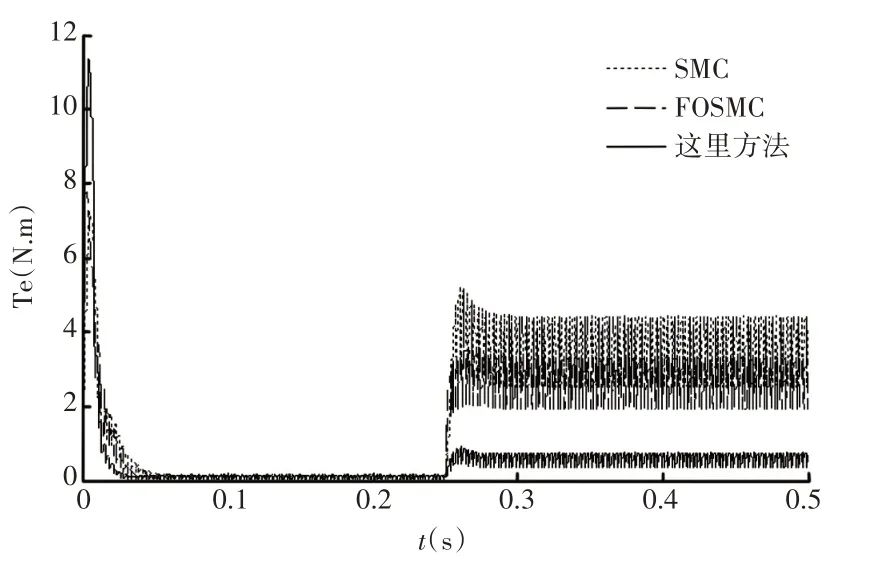
图10电机转矩Fig.10 Electromagnetic Torque of Motors

图9 ～图10表明：①基于本文方法，系统到达稳态的时间最短。②当突加干扰时，基于本文方法的PMSM转速及转矩波动最小，鲁棒性最强。③分数阶滑模控制器的鲁棒性要优于整数阶滑模控制器。

6.2 实验分析

采用TMS320F28335 DSP处理器作为电机主控制器，电机参数与仿真一致。给定转速ωr=1000r∕min，在t=1s，加入负载0.5N⋅m。将实验数据以十进制导入MATLAB，整数阶滑模控制器、分数阶滑模控制器、这里方法的实验结果，如图11～图13所示。

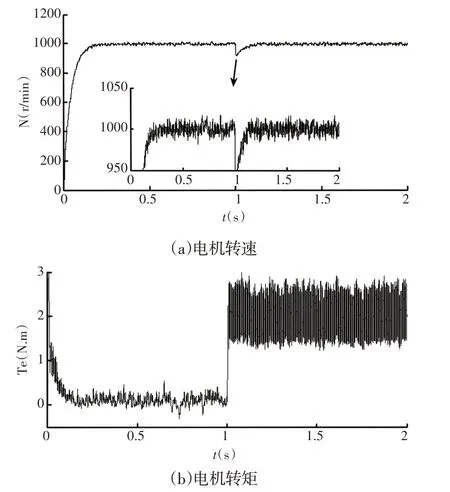
图11 整数阶滑模控制器实验结果Fig.11 Experimental Result of SMC Controller

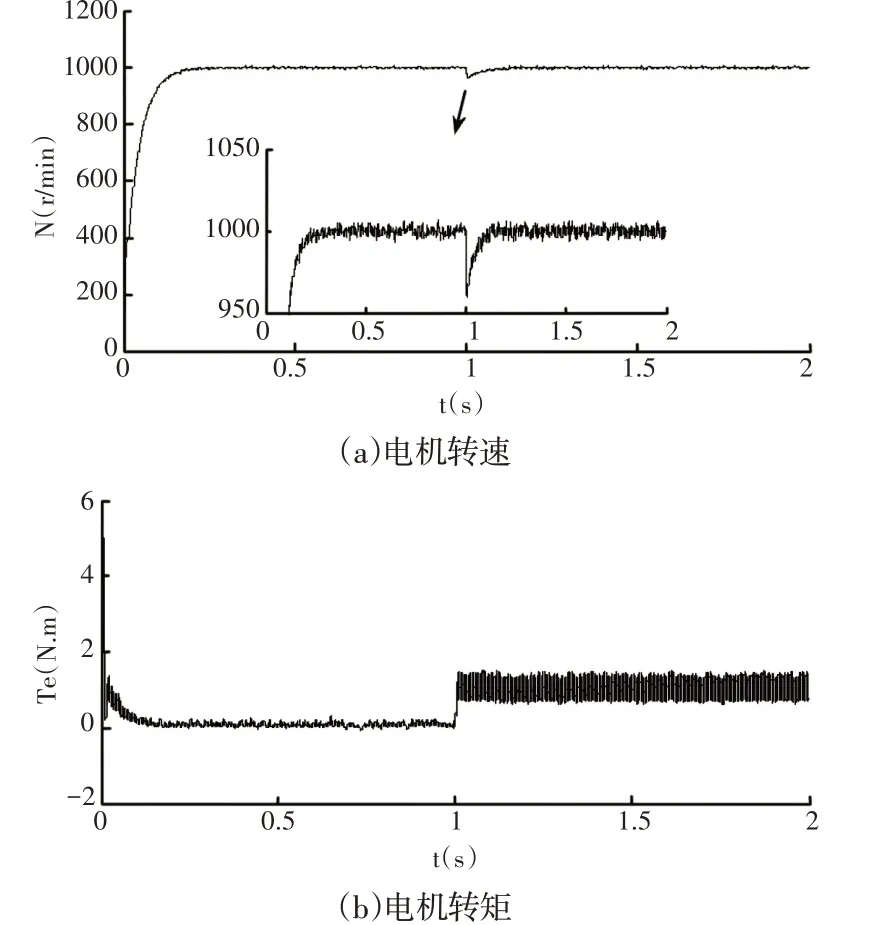
图12 分数阶滑模控制器实验结果Fig.12 Experimental result of FOSMC controller

图13 本文方法实验结果Fig.13 Experimental result of the proposed method

电机实验结果可得出如下结论：（1）实验环境相同的前提下，在3种滑模控制器作用下电机都产生不同程度的转速波动。在加入负载前，本文方法的电机转速波动及电磁转矩波动最小，总体上转速波动范围为（-5，5），其次是分数阶滑模控制器，总体上转速波动范围为（-12，12），整数阶滑模控制器的转速波动最大，总体上转速波动范围为（-23，23）。在加入负载转矩后，同样是本文方法的电机转速及电磁转矩波动最小。可以证明：①模糊自适应参数调节可以有效抑制系统抖振及突加干扰。②分数阶控制器的控制精度和灵活度高于整数阶控制系统，也可以抑制系统抖振及突加干扰。（2）在系统响应速度方面，本文方法的电机转速上升时间最短（约0.2s），其次是分数阶控制器（约0.32s），最后是整数阶控制器（约0.35s）。可以证明：①模糊自适应参数调节可以缩短系统到达稳态的时间。②分数阶控制器的响应速度要高于整数阶控制系统，也可以缩短系统到达稳态的时间。

7 结论

首先，针对PMSM滑模控制器存在抖振过大、性能指标不高等现象，选取分数阶滑模切换S函数，并结合PMSM机械运动方程设计一种分数阶滑模控制器。其次，通过Lyapunov原理和分数阶微积分理论证明了所设计控制器的稳定性。再次，利用模糊算法实现滑模切换项ε和分数阶次λ的在线自适应调节。最后，仿真及实验结果都表明所提方法有效抑制系统抖振，缩短系统到达稳态的时间，并具有较强的鲁棒性。