负荷观测器的轧机单辊传动系统负荷平衡控制
张瑞成,赵 铭
(华北理工大学电气工程学院,河北 唐山 063210)
1 引言
利用多台电机串联对轧机单辊传动是轧机传动系统经常采用的方式,这种传动方式提高了电机的传动功率与传动效率。但是在钢铁轧制的实际过程中,由于传动系统上下电机的实际参数不完全一致、带钢与轧辊之间出现相对滑动等问题,导致上下轧辊的线速度很难保持一致,这将严重影响带钢的质量与设备的安全运行。
为了使轧机单辊传动系统中的多台电机具有良好的速度同步性能,学者们进行了深入的研究。文献[1]采用交叉耦合结构,将两个电机转速作为控制器的输入,通过转速补偿对电机转速进行调节,实现了两个电机之间的同步控制;文献[2]引入主从同步控制结构,电枢电流作为控制器的输入量,实现了立辊轧机交流异步电机的速度同步和转矩同步;文献[3]采用交叉耦合同步控制结构与PI控制器组成同步控制系统,实现了上、下辊负荷的平衡调节。
以上文献虽然实现了轧机电机的速度同步,但是将电机转速或电枢电流作为负荷平衡控制器的输入量,存在很多缺陷,譬如:由于轧制过程是动态的,而且输入量精度不够高,容易产生比较大的误差;在钢铁轧制时,轧辊的实际负载量是不断变化的,造成电机较大的速度波动,进而导致电机的负荷平衡调节效果不佳。
针对上述问题,设计一种新型负荷平衡控制器来保证上下电机输出力矩[4]相等:第一,用负荷观测器观测出来的负载力矩[5-6]作为负荷平衡控制器的输入量;第二,将单神经元自适应PID神经网络[7-8]作为负荷平衡控制器的控制策略。负荷平衡控制器的输出通过交叉耦合结构加载到各电机子系统中,同时在系统中给电机加入一个前馈补偿环节,提高了电机的稳定性及动态性能,同时也改善了系统的同步控制性能。通过仿真实验验证该调速系统改善同步效果的有效性。
2 轧机单辊传动系统机电模型
以上辊直流拖动电机通过连接轴连接轧辊为例,将连接轴看作刚性连接,建立轧机单辊传动系统机电模型,微分方程表达式如下:

式中:id—电机的电枢电流;U—控制电机输入电压;ωm—电机的机械角速度;B—粘性摩擦系数;Cm—电机的转矩系数;J—电机和负载折合到电机轴上的转动惯量;Jm—电机的转动惯量;J L—负载的转动惯量;R、L—电机电枢回路总电阻和总电感;T e、TL—电机的电磁转矩和负载转矩。对以上方程进行拉普拉斯变换,求出相应的传递函数,并推导出的直流电机模型结构图,如图1所示。

图1 直流电机模型结构图Fig.1 DC Motor Model Structure Diagram
3 负荷平衡控制系统结构
3.1 负荷平衡控制器原理
负荷平衡控制器可以解释为控制上下工作辊在相同的时间内输出相同的转矩。若输出转矩不相等,可以调节负荷平衡控制器,给轧辊电机一个外加速度,达到改变工作辊线速度的目的,这样就实现了上下工作辊的负荷平衡。负荷平衡控制系统结构图,如图2所示。
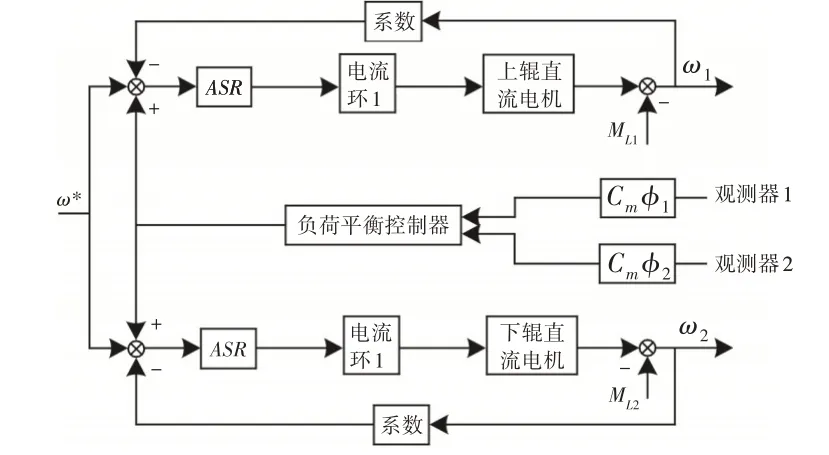
图2 负荷平衡控制系统结构图Fig.2 Load Balance Control System Structure Diagram
为了达到稳定的动态性能和结构上灵活性的目的,上下两台电机采用交叉耦合结构来驱动轧辊。把负荷观测器所观测到的上下轧辊的实际负载力矩值作为负荷平衡控制器的输入参数,当观测值的绝对值之差小于额定转矩的3%时,不进行负荷平衡调节;当两者之差大于3%时,就要进行附加转速调节。将当前给定的速度与负荷平衡控制器的输出量作为附加速度的设定值,该设定值分别作为上下轧辊速度调节器的输入量,实现了速度调节器相等的速度输出,进而满足了上下轧辊的负荷平衡。
3.2 人工神经网络负荷平衡控制器设计
人工神经网络是一种多输入单输出的非线性单元,而且还具有自适应和自学习能力[9-10],可以通过改变突触权值来自学习并自适应目标对象的变化。神经元有比例、积分、微分三个输入维数,它们的系数可以用三个连接权值来近似代替。采用单神经元自适应PID(Single Neuron Adaptive PID)神经网络可以达到良好的同步控制效果,单神经元自适应PID,如图3所示。

图3 单神经元自适应PID工作原理Fig.3 Single Neuron Adaptive PID Working Principle
神经元输入:

神经元特性:

式中:Δu(k)—神经元在k时刻输出的增量;K u—神经元的比例系数;ωi(k)—神经元在k时刻的权值;x i(k)—神经元在k时刻对应的输入值;ηi—神经元学习率。对应的目标函数为:

神经元权值的调整用学习策略p i(k)来完成:

联想式学习策略:

式中:z(k)—教师信号;x i(k)—当前误差信号。
该学习策略采用监督学习,即作用于神经元的教师信号z(k)可以控制环境信息。
目标函数的偏导数按如下方式推导:

学习算法为:
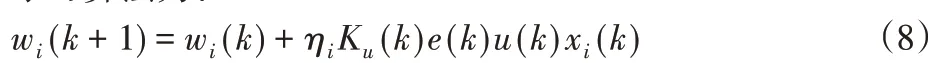
通常情况下,神经元学习率ηi的取值要适中,如果太大,容易造成神经元调节器超调;如果太小,会增加神经元调节器的调节时间,K u的非线性变换修正方法如下[8]。
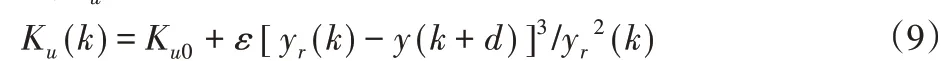
式中:K u0—神经元比例系数稳态初值;ε—调整系数,一般为K u0的1∕10。
系统的稳定性、准确性与快速性取决于K u的大小。减小K u的值,系统的响应时间变长,超调量减小,但是如果K u减小的太多,响应时间会变得过长;若增大K u的值,系统响应时间会变短,超调量增大,但是K u值过大,会引起响应的震荡。所以要根据系统的要求选取一个合适的K u值,保证系统有着更好的稳态性能和更小的超调量。
4观测器设计
轧机主传动系统要求高精度和高动态性能,降低动态速降、缩短恢复时间成为了亟待解决的问题,引入负荷观测器不仅能够解决这一问题,还可以改善系统输出速度的控制精度。
由式(1)可得电机负载与电机转速和电枢电流有关,可以利用检测到的电枢电流与电机转速来构造一个负载力矩观测器。在轧机轧制过程中出现负载扰动的情况下,电机转速、电流会出现相应波动[11],在控制系统中给电机加入前馈补偿可以减弱这种影响,并且可以改善系统的动态性能。轧机轧辊传动方式为:上下轧辊分别由单台电动机单独驱动,其电机负荷观测器原理图,如图4所示。
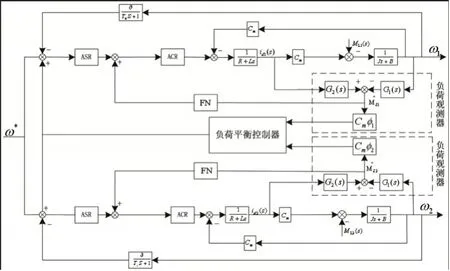
图4负荷观测器原理Fig.4 Load Observer Schematic
如图4负荷观测器原理,两台电机采用交叉耦合结构,每台电机各设置一个负荷观测器。将每台电机的速度ω和电流id分别输入传递函数G1(S)和G2(S)中,构造出负荷观测器,输出观测值经过等效补偿,加载到电机控制信号的输入端。
据图4可得电机转速ω(s)和扰动观测值(s)的方程:


根据式(12)、式(13)可得观测值(s)=M L(s)的条件为:


由式(16)、式(17)可得,负载力矩值可以间接地通过电枢电流与电机转矩系数的乘积、转动惯量与转速微分的乘积这两个综合量来得到。
根据不变性原理,电机加入前馈补偿FN可以抵消或大大减小外部干扰,从而提高负荷平衡控制器的抗扰动性能[12-13]。依据观测器原理与轧机单辊传动系统机电模型可以推导出负荷观测器控制系统结构图,如图5所示。

图5轧机单辊传动系统负荷观测器控制系统传递函数框图Fig.5 Transfer Function Block Diagram of Rolling Mill Single Roll Transmission System Load Observer Control System

为了提高系统的稳定性,需要在FN中添加惯性环节。

为了达到更好的控制效果,令T q=T i,T i为电流调节器环节的等效时间常数,可得补偿器为:,那么加到电流调节器时没有经过微分环节,这种设计方法实现起来方便并广泛应用于工业设计中。
5仿真实验
5.1实验参数
在轧机单辊传动刚性连接系统中,上下两辊直流电机型号相同,但参数不完全一致。其中,拖动电机参数,如表1所示。
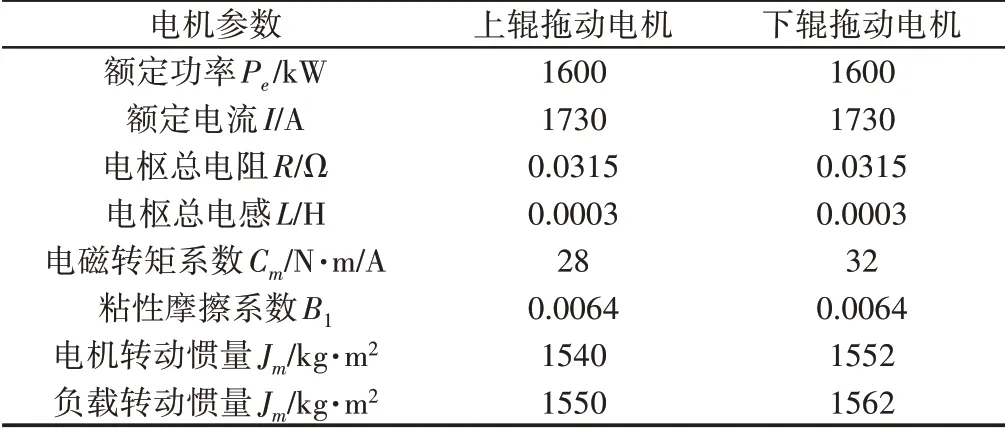
表1上、下拖动电机参数Tab.1 The Parameters of the Drag Motor
两台直流电机的给定参考速度为ω*=23.7rad∕s。
根据单神经元控制率可知,单神经元自适应PID可调参数有5个。学习率ηP、ηI、ηD,神经元比例系数K u和神经元权值ωi(k)。参数分别为,学习率
5.2 仿真结果及分析
文献[3]采用交叉耦合同步控制结构与PI控制器组成同步控制系统,电机电枢电流作为负荷平衡控制器的输入量,实现了上、下辊负荷平衡调节,把该同步控制系统设为系统a。以系统a为基础,引入负荷观测器,并带有前馈补偿环节,设为系统b。用Matlab仿真工具分别对系统a、b进行仿真实验,验证其有效性,仿真结果,如图6~图9所示。

图6 系统a、系统b上辊电机转速对比图Fig.6 Comparison of Roller Motor Speed on System a and System b
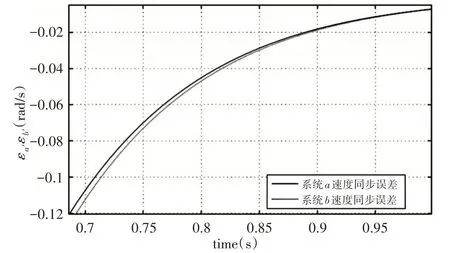
图8 启动阶段速度同步误差对比图Fig.8 Start-up Phase Speed Synchronization Error Comparison Chart
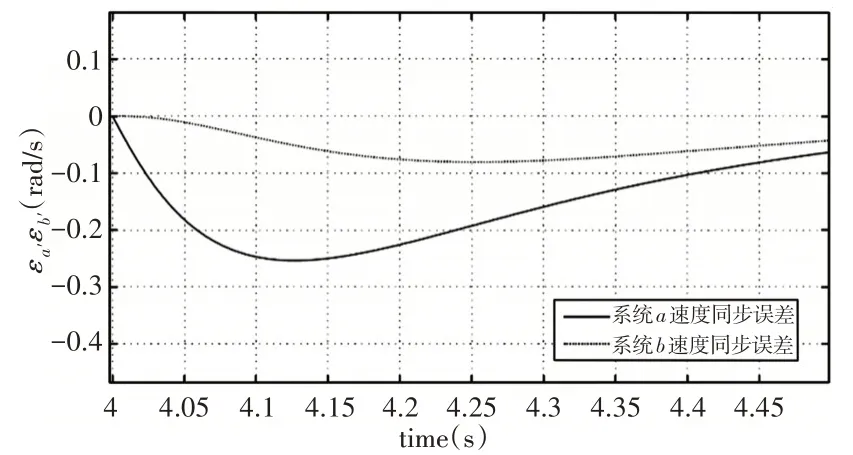
图9 受轧制扰动阶段速度同步误差对比图Fig.9 Comparison of Speed Synchronization Error in Rolling Disturbance Stage
由图6可知,在电机启动阶段,系统a电机上升时间比较慢,到达稳态的响应时间为1.6s,而且动态性能差,容易造成拖动电机故障,传动轴损坏。在受到轧制负载扰动后,产生明显动态速降,其中电机转速达到23.65rad∕s,并且达到稳态的速度较慢,响应时间为6.2s,系统抗扰动能力明显不足。系统b与系统a相比,也产生了动态下降的情况,但是加入了负荷观测器对负荷进行观测并补偿,在调节器的调节下可以较快地实现工作辊的负荷平衡,响应时间缩短到1.175s;回到稳态的实际响应时间更短,响应时间为5.178s,缩短了近16.5%。
由图7~图9可得,两个系统均能使得上下辊电机速度达到同步,且同步精度较高。在(0~4)s期间,系统a的同步误差达到0.0003rad∕s所需的时间为1.437s;4s受到轧制扰动后,系统a的速度同步误差的绝对值开始增大,同步性能开始变差,在(4~4.5)s内速度同步误差为-0.2423rad∕s。系统b引入负荷观测器后,在(0~4)s期间,达到0.0003rad∕s所需的时间为1.46s,达到速度同步所需时间略长于系统a。受扰动后同步误差峰值为-0.0537rad∕s,系统b速度同步误差峰值的绝对值较系统a减小了78%,同步性能明显好于系统a没有负荷观测器的情况。由以上仿真实验结果知,轧制钢材前,系统a与系统b的电机都有着良好的同步性能,扎制期间,负荷观测器的引入增强了系统b的抗干扰能力,并且系统b较系统a有着更好的同步性能,能保证轧辊安全稳定地运行。

图7 有无负荷观测器速度同步误差对比图Fig.7 Comparison of Speed Synchronization Error of Load Observer
6 结论
(1)在轧机单辊传动同步控制系统中,针对轧机电机同步控制性能较差的问题,建立直流电机模型,并把轧辊的驱动电机设计为交叉耦合结构,设计了单神经元自适应PID神经网络的负荷平衡控制器与负荷观测器相结合的控制策略。
(2)通过对电机启动阶段与轧制扰动阶段的仿真分析可得,引入负荷观测器的电机同步控制系统,在轧制前电机到达稳态的响应时间为1.175s,缩短了近26.5%。在轧制期间改善了上下辊电机的同步误差和回到稳态的响应时间,电机回到稳态的响应时间为5.178s,缩短了近16.5%;同步误差峰值的绝对值为0.0537rad∕s,较未引入负荷观测器的同步控制系统减小了78%,保证了轧辊出力均衡。

