柔性机械臂最优抑振轨迹规划与跟踪控制研究

韩键美

（永城职业学院，河南 永城 476600）

1 引言

柔性机械臂具有能耗低、响应快、负载-自重比高、效率高等诸多优点，但是其在工作过程中容易产生振动，不仅降低了定位精度，而且影响机械臂的使用寿命［1］，因此研究机械臂工作过过程中的抑振问题意义明显。

柔性机械臂振动控制方法包括被动控制和主动控制两大类。被动控制方法是在弹性振动产生后使用阻尼方式抑制振动，阻尼结构包括弹性阻尼材料、分流阻尼回路等，此类方法缺点是适用性和鲁棒性差，且增加阻尼材料后也增加了动力学特性复杂度［2］。当前振动控制的研究热点是主动控制方法，主动控制方法是通过设计控制器，主动地减小弹性振动。文献［3］使用其一摄动法将柔性机械臂分为快变子系统和慢变子系统，波那个分别设计控制器实现振动抑制；文献［4］设计了自适应鲁邦滑模控制器，使用传感器和致动器实现了柔性机械臂抑振；文献［5］将输入整形和模糊控制器结合提出了混合模糊控制器，实现了柔性机械臂轨迹轨迹跟踪和振动抑制；文献［6］使用频域辨识和极点配置实现了振动控制。

本文以柔性机械臂抑振轨迹规划和跟踪控制为研究课题。在抑振轨迹规划方面，提出了自适应遗传算法用于轨迹规划；在轨迹跟踪方面，提出了全阶终端滑模控制器，达到了抑制柔性机械臂残余振动的目的。

2 柔性机械臂动力学模型

2.1 柔性机械臂系统

以单连杆柔性机械臂为例，设定柔性机械臂工作在水平面内，如图1所示。图中：Oxy—机械臂坐标系；Ox—轴与机械臂根部轴线相切；Oy轴与Ox轴垂直。Ox0y0—固定坐标系，与初始时刻的Oxy坐标系重合；w(x，t)—t时刻与原点距离为x处（点P）的弹性位移；ψ(x，t)—t时刻点P的角位移；θ—机械臂角位移；JL—关节转动惯量；τ—驱动力矩。

图1 柔性机械臂系统Fig.1 Flexible Manipulator System

为了简化柔性机械臂动力学模型，作出以下假设：（1）机械臂臂长远大于横截面尺寸，即只考虑弯曲变形而忽略剪切变形；（2）将末端负载视为质点。

2.2 柔性机械臂动力学模型

根据弹性理论和假设模态法［7］，t时刻P点弹性位移w(x，t)为：

式中：n—保留模态数；ϕi(x)—第i阶模态振型函数；qi(t)—第i阶模态坐标。根据边界条件可以求得式（1）表达式。

本文使用拉格朗日方程建立柔性机械臂动力学方程，首先求解机械臂系统的动能和势能。机械臂系统动能包括关节处转轴动能、连杆动能和负载动能三部分组成。关节处转轴动能T1为：

式中：JL—关节转动惯量。

记P点坐标为(px，py)，则P点位置和速度为：

则机械臂连杆动能T2为：

式中：lL—连杆长度；ρL—连杆材料密度；AL—连杆横截面积。

负载动能T3为：

式中：vL—机械臂末端速度；mg—负载质量。

由以上推导可得机械臂系统动能T为：

由于柔性机械臂工作在水平面内，因此不考虑重力势能而只需考虑弹性势能，即势能为：

式中：IL—机械臂横截面的惯性矩；EL—机械臂弹性模量，Ki为：

结合式（5）、式（6），根据拉格朗日方程得到柔性机械臂动力学矩阵方程为：

3 最优抑振轨迹规划

3.1 最优抑振轨迹规划模型

将式（8）中的刚性运动和柔性运动进行区分，为：

式中：下标r—刚性运动；f—柔性运动。由上式可得：

式中：W—总振动量；r1、r2—调节系数；tb—机械臂旋转终止时刻。

根据机械臂起始位置、终止位置等基本条件，使用五次多项式规划一条基准轨迹。将工作时间划分为n等份，时间节点依次次多项式规划的θi为基准角位移θBi，以角位移浮动值ΔθCi为优化对象，从而得到各时间节点优化的角位移，而后使用五次多项式样条曲线依次规划之间的运动轨迹，将轨迹曲线代入到式（10）中得到动力学相应，将其代入到式（11）中计算适应度值，依据适应度值评价轨迹优劣程度。

3.2 智能求解方法

遗传算法是模拟生物遗传和自然选择过程而提出的，包括编码、初始种群生成、遗传操作等。初始种群的生成、交叉变异概率对算法寻优性能影响较大［8］，本文从此三个方面进行改进。

（1）染色体编码。使用实数编码方式，对n个角位移浮动值ΔθCi(i=1，2，…，n)进行编码。

（2）初始种群生成。在传统遗传算法中，初始种群的随机产生方法导致初始种群适应度不高，本文提出以均匀方式产生初始种群，方法为：将角位移浮动值取值空间等分成z个空间，在每个空间中均匀产生p个n维染色体，将此z×p个染色体依据适应度排序，选择前N个个体作为初始种群。初始种群的均匀生成方法，保证了染色体的分散性，有利于算法的全局搜索。

（3）自适应交叉操作。交叉操作是染色体进化的主要方式，对于提高种群多样性意义重大。本文提出以种群多样性为依据，自适应调整交叉概率。种群多样性好时使用小的交叉概率，保持种群多样性和稳定；种群多样性差时使用大的交叉概率，提高种群多样性。使用适应度方差和分布熵作为种群多样性的度量。种群规模记为N，第i个染色体的适应度记为fi，平均适应度记为，则第j代种群适应度方差Gj为：

分布熵计算方法为：依照前文将取值空间等分为z个子空间，第i个子空间的个体数量记为Ai，则第j代种群的分布熵Hj为：

其中，pi=AiN。

适应度方差和种群分布熵较大时说明种群分布均匀，进化能力较强。交叉概率随种群多样性自适应变化方法为：

（4）自适应变异操作。变异操作是染色体进化的重要方式，对于较优染色体，变异操作可以破坏优质染色体，因此应使用较小的变异概率；对于较差染色体，变异操作可以使其变异为优质染色体，应使用较大的变异概率。根据以上分析，第i个个体变异概率pmi随适应度自适应变化方法为：

（5）选择操作。以个体适应度为选择依据，每个个体被选概率为，式中f(i)为个体i的适应度值为所有个体适应度之和。这种选择方式既保证了优秀个体被选可能性较大，也保证了任意个体被选可能性，保持了种群多样性。

4 轨迹跟踪控制

滑模控制具有较强的鲁棒性和较快的跟踪速度，本文将其应用于柔性机械臂轨迹跟踪。但是滑模控制存在抖振问题［9］，本文设计了全阶终端滑模控制器，不仅可以抑制抖振问题，而且避免了终端滑模控制的奇异点问题。

4.1 旋转过程中跟踪控制器

以式（9）为基础，令：

则由式（9）可得：

定义轨迹跟踪误差并对其求导为：

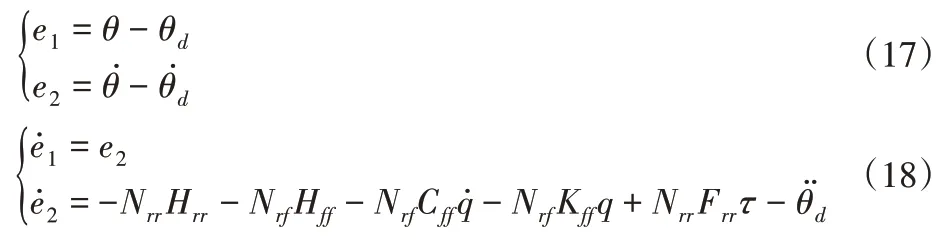
式中：θ为机械臂实时角位移，θd为期望角位移。

为使跟踪误差在有限时间内收敛至0，定义全阶终端滑模面为：

其中，要求c1>0，c2>0，且保证的根在负平面内。a2∈(0，1)，a1=a2(2-a2)。

为了削弱滑模控制器存在的抖振问题，本文使用一阶滤波器设计控制律，为：

其中，η>0、T0>0均为常数，Tu≤-2η。由于控制律中不存在分数次幂项的导数，因此避免了奇异点问题。

下面只需要证明全阶终端滑模面具有稳定性，且在式（20）控制律作用下可使系统状态在有限时间内到达滑膜面，并沿滑模面收敛至零点。

（1）全阶终端滑模面稳定性证明。将式（18）与式（20）代入到式（19），整理得：

对式（22）进行求解，得：

根据式（23）（24）可知：

定义李雅普诺夫函数为：

对式（26）求导，并将式（24）（25）代入，得：

由式（26）（27）可知，全阶终端滑模面具有李雅普诺夫意义下的稳定性。

（2）系统任意状态有限时间内收敛至滑模面证明。记系统由任意初始状态s(0)到达滑模面所需时间为t r，即s(t r)=0。由式（27）可知：

不妨设s>0，则ṡ≤-ηe-T0t，对两边进行积分，则：

同样地，当s<0时依然能够得到式（29）给出的结论，式（29）表示跟踪误差e1、e2可以在有限时间内到达滑模面。

（3）系统状态在滑模面内有限时间内到达误差原点。系统状态在t r时刻到达滑模面（e1(t r)≠0），记跟踪误差在t s时刻运动至零点（e1(t s)=0）。此阶段系统状态在滑模面上运动，即s=0，则根据式（19），有：

式（30）所示误差系统，满足以下条件时：（1）c1>0，c2>0，且保 证p2+c2p+c1=0的 根 在 负 平 面 内；（2）a2∈(0，1)，a1=a2(2-a2)，系统误差可在有限时间内收敛为零。此证明过程可参考文献［10］。

4.2 旋转结束后跟踪控制器

机械臂旋转结束后，对机械臂末端轨迹进行控制，消除机械臂末端的残余振动，使机械臂末端尽快停止在期望位置。根据图1所示柔性机械臂模型，柔性机械臂末端角位移ψ(l L，t)与关节角位移θ关系为：

由于弹性形变量较小，因此arctg(w(l L，t)l L)=w(l L，t)l L，则：

对上式求二阶导数，得：

柔性机械臂旋转结束后控制目标为消除末端残余振动，使机械臂末端角位移ψ(l L，t)尽快跟踪期望角位移ψd=θ(t b)，因此定义旋转结束后跟踪误差为：

对上式进行求导，得到：

定义全阶终端滑模面为：

其中，a3、a4、c3、c4的取值方式与a1、a2、c1、c2完全一致。对于此终端滑模面，设计控制律为：

式中τeq与τes定义方法为：

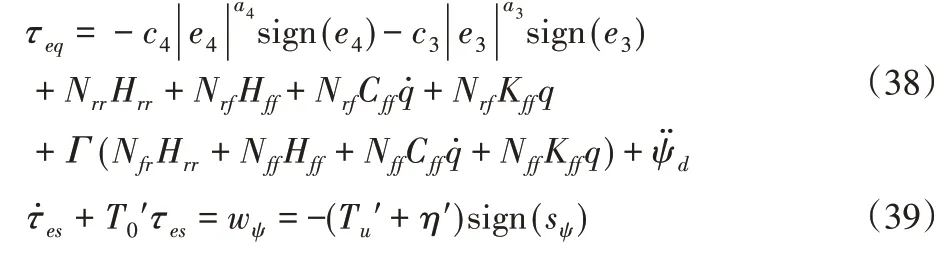
其中，T0′、T u′、η′与式（22）中T0、T u、η的取值方式完全一致。由4.1节证明过程可知，系统状态可在有限时间内到达滑模面，并沿滑模面运动使系统误差为0。

5 仿真验证与分析

本节对两部分内容进行验证：一是对最优抑振轨迹规划方法进行验证，二是对轨迹跟踪控制器的抑振效果进行验证。

5.1 最优抑振轨迹规划

设定机械臂的初始角位移为0，目标角位移为1.57rad。使用五次多项式规划出基础轨迹，然后将其等分为10段，分别使用自适应遗传算法和传统遗传算法对角位移浮动值进行寻优，算法参数设置为：算法最大迭代次数iter=500，染色体个数N=30，需优化的浮动值数n=9，浮动值上下限分别为π8，调节系数r1=0.01，r2=0.99。

分别使用五次多项式、基于传统遗传算法的抑振轨迹规划、基于自适应遗传算法的抑振轨迹规划等方法对柔性机械臂轨迹进行规划。使用五次多项式规划时，以初始点和(t2,θ2)为规划起点和终点，(t2,θ2)至(t,θ)的轨迹与前半部分曲线成点对称。传统蚁群算法与自适应遗传算法的搜索过程如图2所示。

图2 两种遗传算法的搜索过程Fig.2 Searching Process of the Two Genetic Algorithms

由图2可以看出，自适应遗传算法在迭代至50次基本完成收敛，最终收敛值为4.1×10-5，传统遗传算法在迭代至210次时基本完成收敛，最终收敛值为4.7×10-4。由此可以看出，自适应遗传算法具有更快的收敛速度和更高的寻优精度，这是因为种群交叉概率随种群多样性自适应调整，将种群多样性保持在较高水平，提高了算法搜索能力和收敛能力；另外，变异概率根据个体适应度确定，既维护了优质染色体，又提高了较差染色体变优的概率。

传统遗传算法、自适应遗传算法、五次多项式等三种方法规划的轨迹，如图3所示。

图3不同方法规划的轨迹Fig.3 Manipulator Trajectory Planned by Different Method

图3 给出三种轨迹的机械臂末端第一、二阶振动模态如图4所示。

Fig.4不同轨迹的振动量Fig.4 Vibration of Different Trajectory

由图4（a）可以看出，使用自适应遗传算法规划的最优抑振轨迹，机械臂在1s时完成旋转，完成旋转后的一阶模态残余振动极小，在0值附近轻微波动，可以忽略不计；而使用传统蚁群算法规划的抑振轨迹和五次多项式轨迹在1s旋转结束后的一阶模态残余振动较大，振动幅值最大时约为15mm，且在（4～50s时才逐渐稳定，严重影响了机械臂的稳定时间、工作效率和使用寿命。三种方法规划轨迹的二阶模态振动量相差不大，在1s后均稳定在0值附近。综合一二阶模特振动量，基于自适应遗传算法规划的机械臂轨迹具有最优的抑振效果，在机械臂旋转结束后可尽快稳定在目标值附近，振动量极小。

5.2 轨迹跟踪控制器的抑振效果验证

以5.1节中自适应遗传算法规划的最优抑振轨迹为跟踪对象，全阶滑模控制器参数设置为：a1=3 17，a2=3 10，a3=7 13，a4=7 10，c1=6，c2=5，c3=2，c4=3，T0=9，T0′=5，T u=-1.8，T u′=-2.2，η=0.6，η′=0.8。柔性机械臂参数为：机械臂长l=700mm，高h=30mm，厚d=2mm，密度ρ=7.85×103k g∕m3，弹性模量E=2×1011Pa，关节转动惯量J=0.8kg⋅m2。

为了形成比较的效果，使用BP神经网络优化的PID控制方法同时进行轨迹跟踪控制，PID控制器与全阶终端滑模控制器的轨迹跟踪效果，如图5所示。

图5 不同控制器的轨迹跟踪效果Fig.5 Trajectory Tracking Effect of Different Controller

从图5中可以看出，在1s机械臂旋转结束后，在全阶终端滑模控制器的控制下几乎不存在振动现象，而在PID控制器的控制下，机械臂旋转结束后的残余振动幅度较大且振动时间较长，3.5s时振动才减小到较小程度，说明全阶终端滑模控制器对柔性机械臂具有极好的抑振效果和跟踪精度。

在全阶终端滑模控制器和PID控制器的控制下，系统的一阶振动模态位移，如图6所示。

图6 不同控制器的一阶振动模态Fig.6 One Order Vibration Mode of Different Controller

由图6可以看出，在全阶终端滑模面控制器的控制下，不仅机械臂旋转过程中的振动幅度较小，而且旋转结束后几乎不存在残余振动，可以迅速稳定在目标角位置，也说明了全阶终端滑模控制器的控制效果远远优于PID控制器。这是因为在柔性机械臂旋转过程中和旋转结束后，滑模控制器均对机械臂施加控制，使跟踪误差及其导数在有限时间内达到滑模面并移动至零点，达到了极好的抑振效果。

6 结论

本文研究了柔性机械臂的最优抑振轨迹规划和跟踪控制问题，通过仿真验证得到了以下结论：（1）自适应遗传算法相比于遗传算法具有更快的收敛速度和更高的寻优精度；（2）自适遗传算法规划的抑振轨迹在机械臂旋转结束后残余振动远远小于传统蚁群算法规划的轨迹；（3）全阶终端滑模控制器的抑振效果明显优于PID控制器。