双列圆锥滚子轴承优化设计方法研究
周彦沛,毛范海,邱 俊
(大连理工大学机械工程学院,辽宁 大连 116024)
1 引言
早在1985年,文献[1]就对当时已存在的几类轴承优化方法进行了整理。文献[2]以轴承的额定动负荷与额定静负荷为优化目标,建立了圆锥滚子轴承的多目标优化方法。随后,文献[3]提供了双列圆锥滚子轴承结构尺寸的详细计算方法,并以轴承额定动载荷为目标优化得到了双列圆锥滚子轴承的主参数。随着最优化理论的发展,随机算法快速地应用于轴承优化设计中。文献[4]使用遗传算法对滚动轴承进行优化设计,减少了轴承优化问题陷入局部最优的概率。文献[5]采用了多目标遗传算法建立了交叉滚子轴承的优化设计模型,通过优化显著提高了轴承的额定动载荷。文献[6]通过对种群适应度集中程度进行研究,得到了改进的自适应交叉率和变异率,并将其用于轴承的优化设计中。文献[7]利用遗传算法对双列圆锥滚子轴承进行优化设计,并用蒙特卡罗模拟将各个设计参数对轴承的寿命影响进行了灵敏度分析。文献[8]采用多岛遗传算法求解了双列圆锥滚子轴承优化模型,并通过IN⁃SIGHT优化软件分析得到了各个优化变量对轴承寿命的影响。
综上,现有的轴承优化设计方法多以轴承的基本额定动载荷或寿命为优化目标,这类优化方法可以在确定的轴承外形尺寸下获得承载能力更大的轴承。然而,其也存在两处弊端。一方面,该方法设计流程繁琐、设计周期长,由于在轴承优化设计时没有考虑载荷对轴承设计的影响,因此采用这类方法设计完成轴承后,需要再次对轴承各项性能进行校核,若轴承性能不满足设计要求则需要调整参数对轴承重新设计。另一方面,在进行轴系结构设计时,往往希望在保证轴承各项性能要求的情况下得到更紧凑的轴系结构,而上述方法的优化目标显然与这一实际的工程问题不相一致,因此该方法设计的轴承过于保守,设计出的轴承性能一般也是“过剩”的。
为了解决这一难题,这里建立了以轴承体积为优化目标的优化设计方法,对轴承的几何关系、滚子接触应力和轴承修正寿命进行了约束,通过遗传算法优化得到了在给定工况载荷下既满足应力和寿命要求且体积最小的双列圆锥滚子轴承。在满足同样性能要求下,优化后的轴承与原先采用的轴承相比体积减少了22%。本方法不仅大大缩短了轴承设计周期,而且节约资源、降低了成本。
2 双列圆锥滚子轴承优化模型建立
2.1 优化目标
双列圆锥滚子轴承结构参数,图中:d—轴承内径,mm;D—轴承外径,mm;B1—轴承内圈宽度,mm;C1—轴承外圈宽度,mm;Dpw—轴承滚子组节圆直径,mm;α—接触角,°;φ—半锥角,°。如图1所示。

图1 双列圆锥滚子轴承结构Fig.1 Double Row Tapered Roller Bearing Structure
通常情况下,选用轴承时,总希望找到一个既能满足轴承各项性能要求且体积又小的轴承。这样不仅能减小整个轴系结构尺寸,又能减少材料、降低成本。故这里将轴承的空间体积作为优化目标,其计算公式为:

其中,轴承内径d、外径D和轴承宽度B1与优化变量之间的详细几何关系的推导参见文献[3]。
2.2 优化约束
在建立轴承优化模型时,除了考虑到轴承几何约束,还对轴承的修正寿命和滚子接触应力进行了约束。
轴承的寿命计算可参考文献[9]。在轴承优化中,需要对滚子的接触应力进行约束,首先由文献[10]轴承内部载荷分布计算方法,求解出滚子最大接触载荷。按照Hertz接触理论,滚子和滚道接触时其表面压力可看成椭圆柱分布,滚子最大接触应力的计算方法参见文献[11]。
在轴承优化时,需要对轴承结构尺寸的几何关系、滚子最大接触应力和轴承的修正寿命进行约束,具体的约束条件如下:


约束1~6是为了保证轴承的内外径和宽度在规定的设计尺寸范围内。其中,dmin—轴承内径下限,mm;dmax—轴承内径上限,mm;Dmin—轴承外径下限,mm;Dmax—轴承外径上限,mm;B1min—轴承宽度下限,mm;B1max—轴承宽度上限,mm。
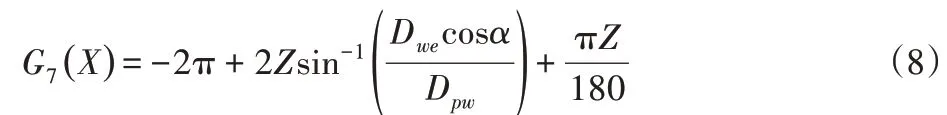
约束7是为了避免滚子间的相互碰撞而设置的滚子个数约束。其中,Dwe—滚子平均直径,mm。

约束8和约束9是为了保证滚子的长度和直径比值在某一确定的范围内。其中,KLDmin—滚子长径比的下限系数,KLDmax—滚子长径比上限系数。

约束10是为了保证轴承在极限载荷工况下,滚子最大接触应力在许用应力范围内。式中,σ1max—轴承在极限载荷工况下滚子的最大接触应力,MPa;[σ1]—轴承在极限载荷工况下的许用接触应力,MPa。

约束11是为了保证轴承在疲劳载荷工况下,滚子最大接触应力在许用应力范围内。其中,σ2max—轴承在疲劳载荷工况下滚子的最大接触应力,MPa;[σ2]—轴承在疲劳载荷工况下的许用接触应力,MPa。

约束12是为了确保轴承在疲劳载荷工况下,其寿命达到期望寿命。其中,t—轴承的期望寿命,(年);tm—轴承在疲劳载荷工况下的修正寿命,(年)。
2.3 优化变量
双列圆锥滚子轴承在正常工作条件下的失效形式主要是套圈内表面的裂纹或断裂、滚道的压痕、磨损和接触面疲劳破坏等。而这几种失效可通过限制轴承最大接触应力和保证轴承最低疲劳寿命来预防。因此,确定轴承优化变量时,将影响这些性能要求的轴承主参数作为优化变量。因此优化变量可以表示为:X=
2.4 优化算法与设计流程
在双列圆锥滚子轴承优化设计中,优化约束较多且相应的函数计算较为复杂,其中修正寿命计算和轴承接触载荷的计算属于非连续性函数问题的求解。采用一般的最优算法往往容易陷入到局部最优解中,而遗传算法通过交叉变异的方式具有很好的全局搜索能力来寻找本优化模型的最优解。
在遗传算法中,为了使可行解种群朝着更好的方向进化,每个个体都可以发生交叉或变异遗传。进化通常从一组随机生成的种群开始迭代,每次迭代的种群称为一代。交叉率为1意味着所有的后代都是交叉后代,而不同的交叉率对最终的优化结果有着较大的影响,因此选择合适的交叉率非常重要。因此本算法分析了不同的交叉率对优化目标值的影响,以找到该模型下的最佳交叉率。最终,本算法的优化设计程序框图,如图2所示。
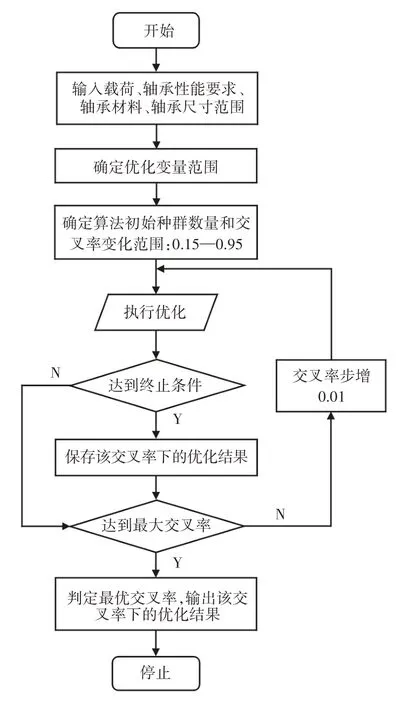
图2 算法流程图Fig.2 Algorithm flowchart
3 双列圆锥滚子轴承优化算例
某风机主轴承运行时,在极限载荷工况下的等效径向力为4700kN,轴向力为850kN;在疲劳载荷工况下的等效径向力为840kN,轴向力为300kN。轴承设计时,所采用轴承钢的弹性模量为2.06×106N∕mm,泊松比为0.3。轴承工作条件与性能要求,如表1所示。

表1 轴承工作条件与性能要求Tab.1 Bearing Working Conditions and Performance Requirements
根据轴结构参数,轴承内径变化范围为(800~810)mm,外径变化范围为(900~1100)mm,轴承宽度变化范围为(150~250)mm。根据相关的技术文件,优化变量的取值范围,如表2所示。

表2 优化变量范围Tab.2 Optimization Variable Range
本算例分析了(0.15—0.95)间的交叉率对优化结果的影响,并找到了该优化模型下的最优交叉率,如图3所示。

图3 不同交叉率下的优化结果Fig.3 Optimization results at different crossover rates
图中,黑色曲线表示在不同交叉率下优化出的轴承体积的变化情况。可以看出当交叉率在(0.15~0.95)间变化时,体积的变化范围为(81~85)dm3之间,体积波动变化量占总体积不到4%。图中红色圆圈处表示最佳交叉率0.58处的体积大小,为81.25dm3。
将本算法优化出的参数与原先选用的轴承进行对比,从本算法优化结果可以看出,轴承寿命为21年接近寿命边界值,因此寿命是影响该轴承体积减小的一个主要约束。轴承在极限载荷下,原先轴承的接触应力为1895MPa远低于许用应力2800MPa,在疲劳载荷下其修正寿命为40年也远高于期望寿命20年。原先的轴承体积为104.46dm3,本算法优化出的轴承体积为81.25dm3,在满足同样性能要求下,优化后的轴承体积减少了22%。因此,原先使用的轴承设计过于保守,浪费了资源、增加了成本,如表3所示。

表3 原先轴承与本算法优化结果对比Tab.3 Comparison of Original Bearing and Optimization Results of This Algorithm
4 结论
对双列圆锥滚子轴承的几何关系、寿命计算方法、滚子接触载荷和滚子接触应力进行了分析,提出了以轴承体积作为优化目标的优化设计方法。在给定的载荷下,通过遗传算法优化得到轴承的关键参数,并给出轴承校核结果。分析了不同交叉率对优化结果的影响,找到了最优交叉率。通过该优化方法对某风机主轴承进行了优化设计,并给出了其结构尺寸和极限载荷下的接触应力与疲劳载荷下的修正寿命。
本算法将轴承各项性能作为约束条件,引入到轴承优化设计中,极大简化了轴承“设计—校核—再设计”这类繁琐的设计方法,更缩短了轴承设计周期。将本方法优化出的轴承与原先使用的轴承进行了对比,在同时满足轴承性能要求的前下,本设计方法设计出的轴承体积减少了22%,节约了资源,降低了成本。

