AHP+改进模糊综合评价法在财务共享服务中心构建选址决策中的应用研究
梁彩情 亳州学院经济与管理系
引言
A集团是以从事煤炭开采、加工和销售的综合性企业,由于企业规模不断壮大,财务效率低下、管理成本增大等问题日益凸显,需要通过构建财务共享服务中心来解决这些问题。通过构建财务共享服务中心将各个业务单位的财务业务大部分迁移至财务共享服务中心所在地,进行集中业务处理,达到节约成本、加强集团管控力、提高财务管理效率等目标。考虑迁移过程中产生迁移成本,迁移场所选择是建设财务共享服务中心一个主要环节,关系整个集团战略目标实现,需要引起重视[1]。那么究竟在哪里选址建设财务共享服务中心?需要考虑的因素有哪些?这些问题值得我们去认真思考和筹划[2]。通过对以往的案例研究可以发现,集团在构建财务共享服务中心选址决策时,往往是通过专家对成本投入、人力资源、网络通信、交通便捷、当地的政策规则、当地经济发展水平几个方面,进行主观综合判断,确定构建选址。这样做不合理之处:影响因素本身具有模糊性特点,专家根据经验进行判断,显得主观性太强;由于财务共享服务中心选址不仅受到城市环境因素和公司内部因素的影响,对于跨国公司还受到语言差异、文化差异等因素影响,如果在选址决策时单凭主观分析判断,有可能导致选址决策失误。鉴于此,本文采用层次分析法和模糊综合评价法相结合方式,构建具体可量化的财务共享服务中心选址模型,将人的主观判断用数量形式表达和处理,尽量减少个人主观臆断所带来的弊端,使评价结果更可信,使选址决策更加科学、合理,从而助力财务共享服务中心价值的发挥。本文选取A集团作为案例进行研究,通过构建综合评价模型对备选城市西安、太原、郑州、大同进行评价,确定最适宜构建财务共享服务中心的地址。
一、基于AHP+改进的模糊综合评价法建立财务共享服务中心选址决策的评价模型
模糊综合评价法是通过建立隶属函数对模糊对象从定性分析转化为定量分析,具有对多因素、多层次的复杂问题评判效果比较好等方面的特点。A集团构建财务共享服务中心选址受多种因素影响,适合采用模糊综合评价法进行综合评价。首先采用层次分析法确定评价指标权重,将评价指标进行量化,然后选择加权平均模型M(·,+)替换M(∧ ∨)。
(一)层次分析法确定各层次指标的权重
1.构建财务共享服务中心选址的指标体系
本研究采用层次分析法建立财务共享服务中心选址的综合评价指标体系,根据对已经建成财务共享服务中心案例研究、相关行业专家指导意见以及管理高层考虑因素,建立了三层级指标体系。具体的评价指标体系如表1所示。
2.构造判断矩阵
根据表1指标体系,首先建立一级评价指标因素集合B={B1,B2,B3,B4}以及二级指标因素集合Bi={Bi1,Bi2,Bi3,…,Bin}其中(i=1,2,3,4),其次对一级指标因素之间或隶属于同一个指标的二级指标因素之间根据相对重要性进行两两比较,同时采用1-9标度(如表2所示)对比较结果赋予具体数字进行量化,进而形成判断矩阵 U,设判断 U=(aij)m×n,其中 aij>0,aij=1/aji(i,j=1,2,3…,n)。

表1 A集团构建财务共享服务中心选址评价指标体系

表2 AHP法1-9标度赋值原则
3.计算因素权重值
采用根法将判断矩阵每行元素相乘后再开n次方,计算出判断矩阵的特征向量。即:


4.判断矩阵一致性检验
具体步骤如下:
(1)计算一致性指标CR
(2)查找相应的平均随机一致性指标RI。对n=1,2,…,9,Saaty给出了RI的值,如表3所示。

表3 平均随机一致性指标RI
(3)计算一致性比例CR

当CR<0.10时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当的调整。
(二)建立模糊评价矩阵并进行模糊综合评价
1.选定评语集
根据研究对象的特点,本文建立评语为优秀、良好、一般三个等级,评语集合=(优秀、良好、一般)。为了计算方便,对评语集V进行量化,将评语等级依次赋值为90、70、50,即对应的数值集。具体见表4评价定量分级区间。

表4 评价定量分级区间
2.建立模糊综合评价矩阵
对二级指标因素集合Bi={Bi1,Bi2,Bi3,…,Bin}中每个单因素按照评价集合中的评价等级进行单因素评价,并对每个单因素进行量化,得到单因素模糊评价矩阵,如果对n个元素进行综合评价,得到一个n×3的单因素模糊评价矩阵Ri。
3.进行模糊综合评价
通过模糊矩阵乘法计算,将二级指标权重集合Wi与评价矩阵Ri进行模糊运算,即:Bi=Wi×Ri,得出一级模糊综合评价集,同时作为一级指标的隶属度矩阵设为R。由一级指标权重集合W与矩阵R进行模糊运算得到二级模糊综合评价集,即:G=WT×R,将综合评价集合G与数值集N相乘得到选址的综合评价结果,由得分最高城市的作为最佳备选选址。
二、A集团财务共享服务中心构建选址综合评价
(一)应用层次分析法确定各层指标的权重
1.确定一级指标的权重
步骤:① 构造判断矩阵G;② 采用根法计算判断矩阵特征向量;③ 对特征向量进行归一化后得到权W;④ 检验判断矩阵G一致性,详细结果见表5所示。

表5 Bi对于G的判断矩阵(i=1,2,3,4)
2.确定二级指标的权重
根据上面一级指标确定的方法,同理分别计算13个二级指标的权重,详细计算结果见表6~9所示。

表6 B1j对于B1的判断矩阵(j=1,2,3,4)
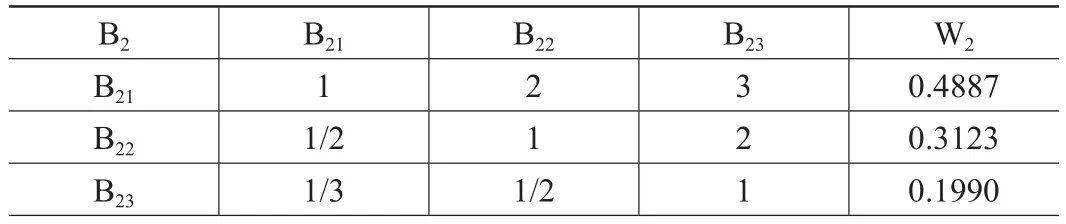
表7 B2j对于B2的判断矩阵(j=1,2,3)

表8 B3j对于B3的判断矩阵(j=1,2,3)

表9 B4j对于B4的判断矩阵(j=1,2,3)
根据计算结果,一级指标和二级指标的权重计算结果详见表10所示。

表10 各层指标权重
(二)A集团构建财务共享服务中心选址的模糊综合评价

1.一级综合评价
根据专家打分对各个二级指标进行单因素评判从而建立一级单因素评判矩阵。下面以太原备选地址进行案例分析,对迁移成本B1在物流费用B11、员工迁移意愿B12、员工迁移成本B13、建设期沟通成本B14进行评价,评价结果见表11所示,表中的数字代表专家对每个单因素不同评价等级的数量。

表11 20名专家对迁移成本评价结果
由表11构造单因素模糊评判矩阵R1。即:

2.二级综合评价
根据二级指标各个单因素评价矩阵通过模糊矩阵复合运算,得到备选地址西安的四个一级指标单因素评价矩阵B1、B2、B3、B4,即:

(三)评价结果分析
计算结果:太原市得分为72.95,西安得分为70.71,郑州得分为64.92,大同得分为59.95。太原、西安、郑州的评价等级为良,大同评价等级为一般,由于太原市综合评价分数最高,因此选择太原市作为最佳构建财务共享服务中心选址。
结语
在A集团构建财务共享服务中心选址中,本文采用AHP确定影响选址因素的各个指标权重,并进行一致性检验,采用改进的模糊综合评价法对备选地址的各项指标进行综合评价,并得出最终的评价结果,根据评价结果得分进行排序,得分最高者为最佳构建选址。太原市得分最高,作为A集团最佳构建选址。通过构建选址的模糊评价数学模型,使A集团在构建选址中出现的模糊问题能够量化处理,为管理决策提供科学、合理的依据,使管理决策结果更具有说服力。

