单元组合下的齿轮轮系运动方案分析*

赵永生,辛超超,马雅丽,刘颜铭

(大连理工大学 机械工程学院,辽宁 大连 116024)

0 引 言

关于齿轮轮系的运动分析,国内外学者目前还一直采用以往的设计手段。而要形成一个关于齿轮轮系的运动分析新方案,往往需要依靠设计人员大量的从业经验。生成满足功能需求的新方案存在着一定的难度,对于多工况条件下的复杂齿轮轮系运动方案而言则更加困难。同时,已生成的方案的优劣又受设计者设计理念、创新能力和设计水平的制约;设计过程中尚没有可利用的软件,计算机辅助齿轮轮系方案设计的瓶颈是缺少真正意义上的产品设计理论模型与数字化设计平台的支撑。所以，有必要将设计理论和设计方法相结合,来支持计算机协助轮系运动方案的设计[1-4]。

针对机械系统的运动方案,国内外研究人员已做了广泛研究[5-7]。HSIEH H L等[8]以基本轮系作为研究对象,提出了一种分析行星轮系速比的手段,研究了整体轮系的运动特性。邢庆坤等[9]通过对单个杠杆系统进行分析来取代行星排,并对其杆点进行了深入研究。WANG J等[10]分析发现了一种新的拓扑方法,用以表示行星轮的传动,并基于数学组合理论,获得了行星齿轮组基本部件的3种组合。QIAN F[11]等为了研究运动/力传递的构型特性,将机械系统的构型综合扩展到状态空间法,进行了积分综合机制配置。段钦华、薛会玲等[12,13]给基本轮系做出了定义,并研究了一些复杂轮系的运动特点。张利彬等[14,15]通过对机械系统中的运动方案进行分析,得到了新的见解,并对串联机构进行了深入研究,但其研究中并没有提及混联组合机构。张丽萍等[16]在分析简单机构单元之后,建立了一个信息表达体系,其中包含机构运动特性。李斌等[17]参考行星齿轮机构的运动特性,通过对一种行星齿轮机构矩阵运算进行分析,得到了一种多排行星齿轮机构构型问题的替代方法。

当前学者的主要研究对象是机械系统运动方案,对于齿轮轮系运动方案设计的研究还没有形成完善的理论体系。在此研究基础之上,本文对齿轮轮系单元组合约束与组合方式进行分析,获取特征矩阵的拆分方法,以此完成对齿轮轮系运动的求解。

1 单元组合的运动特征状态模型

1.1 基本单元与复合单元

齿轮轮系运动方案设计阶段重在研究运动变换。在运动方案设计层面上,齿轮系统由表征运动变换特征的机构构成。因此,运用单元化的机构来研究齿轮轮系运动方案的设计,可以对复杂问题进行简单化处理。

基本单元的机构简图如图1所示。

图1 基本单元的结构简图

单自由度、双自由度以及能够明确表达运动特征变换功能的齿轮机构均称为齿轮轮系的基本单元。基本单元是轮系中最基础的功能转变机构,同时也是复杂轮系设计与分析的基础目标。

一些简单复合单元的结构简图如图2所示。

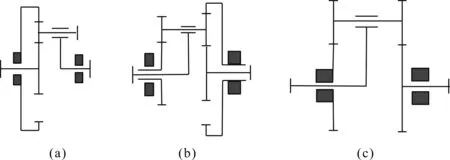
图2 复合单元的结构简图

在分解轮系时,笔者发现了一个非最基本运动表征转换的子轮系。由于齿轮轮系运动方案研究过程当中不涉及单元的具体细节,仅用到单元的输入与输出运动特征,这类能够被研究和组合的单元化机构称为复合单元。

每个单元均存在专属的运动特征向量及状态方程。单元运动方程为:

ko=K·ki

(1)

式中:ki—单元的输入运动向量;ko—单元的输出运动向量;K—运动特征状态矩阵。

基于单元的齿轮轮系组合可以推广到多个单元的组合当中,本文将讨论如何进行单元组合以及组合模型的表达。

1.2 单元组合约束

齿轮轮系运动方案单元化设计的重点是单元之间的组合,在分析单元组合方式之前必须要研究单元之间的组合约束。复合单元的组合约束方式和基本单元一致,本文把基本单元组合作为研究对象。

(1)运动约束

两种基本单元的构件相连方式通常是刚性连接。在研究构件连接时需要考虑运动约束,即前后两单元在连接条件下运动特征必须保持一致,换言之,即具有相同的转速。

组合轮系如图3所示。

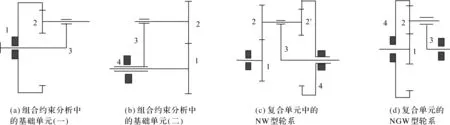
图3 组合轮系

NW轮系由两个行星轮刚性相连在一起,沿着相同轴线进行行星转动。本研究仅加了运动约束,两个齿轮具有同等转速以及不一样的结构参数。

(2)结构约束

前置单元所输出的构件以及后置单元所输入的构件在连接时,所有与结构参数相关的约束称为结构约束。研究构件相连时,如果行星轮与行星架各自组合成单独构件,那么它们之间要具有一致的转速和参数。

此外,结构约束还包含由中心距关系所引起的约束,即组合之后轮系的构件轴线必须同主轴线完全重合。

在图3(d)中有:

r11-r12=r21+r22

(2)

式中:r11—基本单元U1的齿轮1的半径。

如果相连两个行星轮模数一致,所有单元的齿轮齿数间就会有一定关联。约束能够用各齿轮齿数关系代替中心距关系,即:

z11-z12=z21+z22

(3)

式中:z11—基本单元U1的齿轮1的齿数。

双联齿轮中则出现行星轮刚性连接,参与连接的两个行星轮模数不相同。

(3)自由度约束

基本单元在组合之后自由度发生了变化,原因在于组合过程中构件与运动副之间产生连接;基本单元机架也在进行组合时参与其中。基本单元仅单一机架连接的方式有两种:固定机架间的合并、运动构件和相对机架的合并。这里只讨论固定机架的合并。

齿轮轮系当中一般包含有两类组件:系杆与齿轮。所以,基本组合后的系统自由度为:

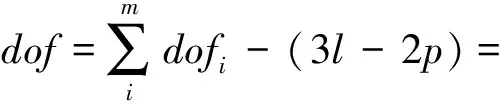
(4)

式中:dof—组合后系统自由度;dofi—第i个单元自由度数;m—参与组合的单元数量;l—参与连接的运动构件数;p—减少的转动副数。

笔者创建构件连接方程,并给上述运动约束做出描述。如果前一个单元j的第m个构件与后一个单元j+1的第n个构件相连接,则运动特征传递方程为:

(5)

式中:k—运动特征向量;C—连接矩阵。

1.3 单元组合方式

(1)串联组合方式

第一个单元的输出与第二个单元的输入构件相连接。

正常单元串联组合如图4所示。

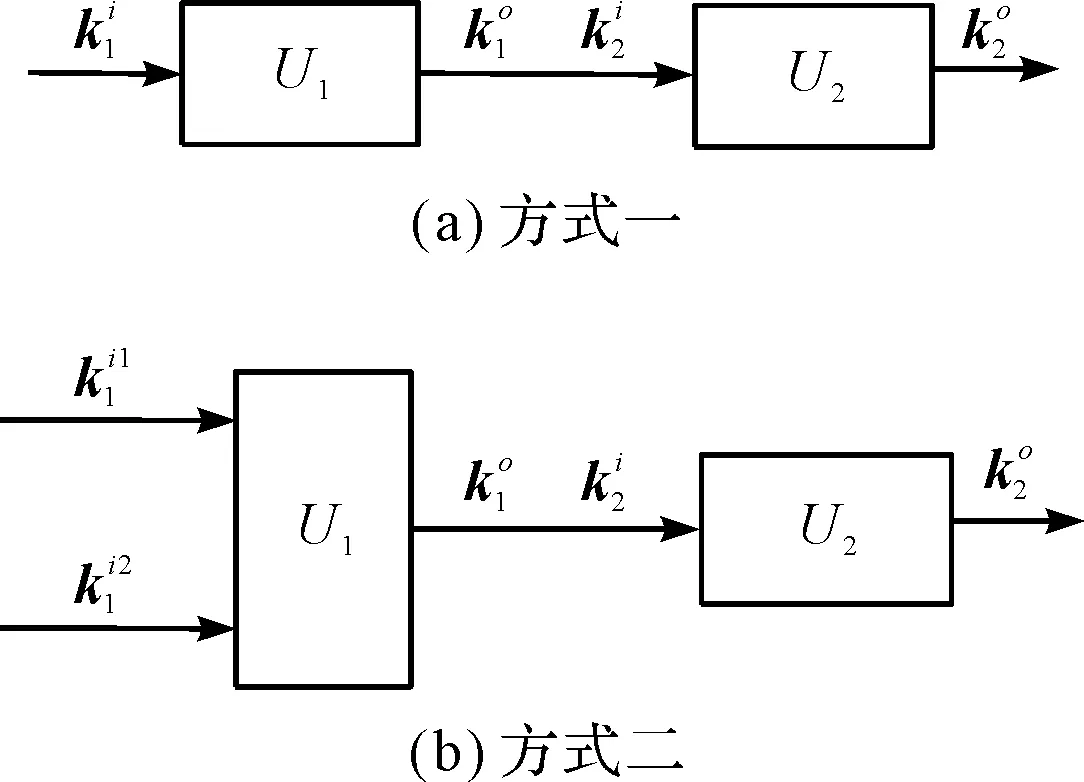
图4 串联组合方式

(2)并联组合方式

两个单元输入构件或输出构件连接。单元并联组合方式的运动特征为运动并行传递。

常见单元并联组合如图5所示。

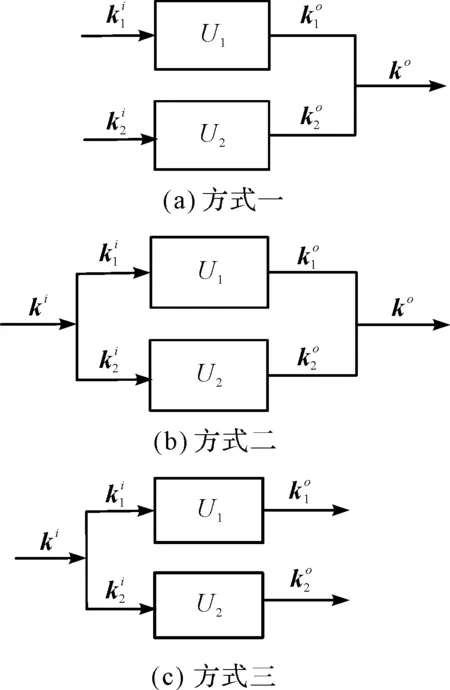
图5 并联组合方式

(3)混联组合方式

在齿轮轮系当中,混联的组合方式包含串联与并联两种组合。

比较常见单元混联组合方式如图6所示。

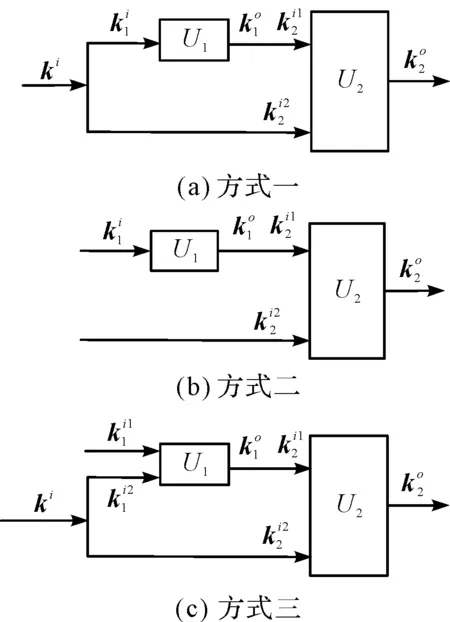
图6 混联组合方式

1.4 单元组合的特征状态模型

(1)串联组合的运动状态关系式

串联组合的运动模型表达了串联系统的两种传递方式之间状态的转变。在图4(b)中,U1、U2分别是双、单自由度单元,其运动关系式如下:

(6)

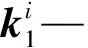
单元U1和U2之间的连接方程为:

(7)

依照单元的运动方程与连接公式,可得出串联组合的运动特征方程为:

(8)

(2)单元并联组合运动特征状态方程

如图5(c)所示,单元U1、U2是单自由度单元,U1、U2的运动特征状态方程为:

(9)

(10)

(3)混联组合单元的运动特征方程

在图6(c)中,单元U1、U2是双自由度的单元,其运动特征状态方程为:

(11)

(12)

进一步地,可得到混联组合运动特征方程为:

(13)

2 运动方案综合

轮系运动方案研究是在明确齿轮之间传动比以及转速情况下,根据单元组合获取符合较大传动比与符合复杂运动变换功能需要的齿轮轮系;根据需求,获取特征信息,得到特征状态矩阵。

若用许多单元组合来完成轮系运动特征变换,则必须对矩阵进行拆分,对拆分步骤建模,为利用计算机手段完成矩阵分解过程提供依据。

本文首先讨论运动状态矩阵的拆分。

2.1 运动特征状态矩阵的分解

由已有的研究可知,轮系运动方案分析的重点为拆分特征矩阵,即齿轮轮系传动比特征的分解。

在明确轮系的输入与输出特征向量情况下,分析轮系可行解,可通过把齿轮轮系中的特征状态矩阵拆分为多个特征状态矩阵的相加与相乘,然后运用各个特征状态矩阵到数据库中查找对应的集合,接着完成序列组合。

2.2 运动特征状态矩阵的分解算法

依据齿轮轮系单元的常见组合方式和运动特征状态矩阵的分解规则,每个组合方式关联不一样的状态矩阵拆分算法。本研究分析两个单自由度单元串联组合的运动特征矩阵的分解算法。

先给定轮系的特征状态矩阵是K,K能够拆分成n个矩阵乘积:

K=K1·K2…Kn-1·Kn

(14)

运动特征状态方程分解原理如图7所示。

图7 串联组合矩阵分解原理图

此处引入霍夫曼树理论,当轮系的特征矩阵分解一次,就形成两个特征矩阵乘积;要进行再分解时,需对这一级的两个矩阵中的一个或两个进行分解,直至无法分解为止。

2.3 运动方案设计步骤

齿轮轮系单元库中保存有各基本变换单元的传动比、输入转速等设计需求,需要通过拆分运动特征矩阵,匹配获得单元,然后再进行组合,得到运动方案,即:

(1)依照设计要求,能够获取齿轮轮系系统的特征状态矩阵K;

(2)搜索特征矩阵是K的复合单元与基本单元。分析符合系统方程的单元是否存在,若存在,则把可行解作为输出;

(3)如果不符合步骤(2),则必须对系统的特征矩阵进行拆分。按照组合方式的分解算法做出拆分。通过对状态空间的理论进行分析,在确定特征方程拆分规则之后,把已完成的分解算法进行传动比分解计算,并根据分解条件,考虑是否具有可分解计算的可能性,如果是能够分解的,则进一步计算,最终能够得到系统中单元的特征方程;

(4)搜索单元的数据库,分析满足方程传动比的特征单元存在与否,进而获得单元与组合系统的方案集;

(5)通过组合约束的条件,找到能够满足设计需求的方案。

3 设计实例

以某型号风力发电的变桨齿轮箱齿轮轮系运动方案设计为例。其设计需求为:

(1)输出转速:0～15 r/min;

(2)总传动比:100;

(3)输入转速:1 500 r/min;

(4)单输入、单输出。

运动方案求解过程如下:

(1)确定向量的元素为输入、输出转速w,输入与输出运动状态向量为:

(15)

(16)

(2)确定输入轴的个数为1、输出轴的个数为1,根据满足需求的单元组合方式确定系统特征状态方程,并提取特征状态矩阵。先计算一个单元是否满足需求,再确定两个单元串联组合是否满足传动比需求,以此类推。每次计算完成,增加一个单元数再重新计算,直到达到级数上限。按照3种组合方式分别计算如下:

①串联。当单元组合方式为串联时,满足需求的串联组合方式的单元组合图示为图4(a),其特征状态方程如图8所示。

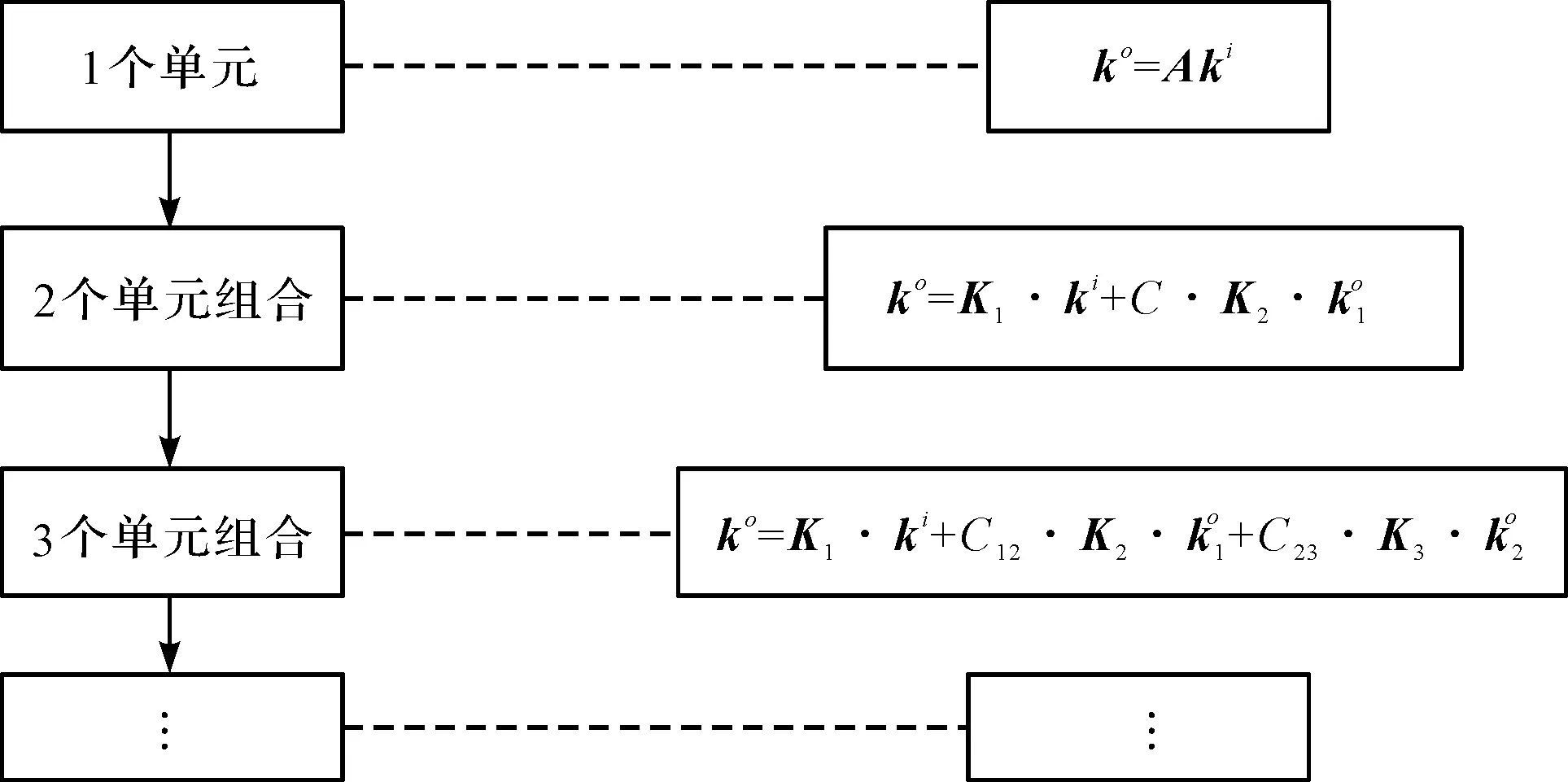
图8 不同单元数串联组合的计算公式

②并联。当单元组合方式是并联时,符合需求的单元组合图示为图5(b),其特征状态方程如下:

(17)

③混联。当单元组合方式为混联时,满足混联组合方式的单元组合图示为6(a),其特种状态方程如下所示:

(18)

(3)选择组合形式进行匹配。

利用单元库求出同时满足条件的组合。通过本文计算方法,可得到多种设计方案。

下面给出3种组合方案,选择更多单元组合可以得到更多的设计方案,尽管系统要复杂一些,利用方案评价体系,可以选出合适方案,实现方案的创新设计。

运动方案结果举例如图9所示。

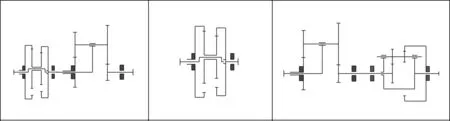
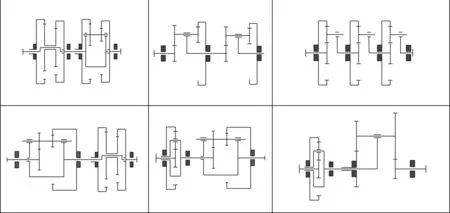
图9 运动方案结构简图

图9结果表明:

(1)特征矩阵的拆分方法是高效且可应用的,在风力发电的变桨齿轮箱齿轮轮系运动方案求解中,共获得了9种运动方案结果;

(2)该分析方法可为实际工程中齿轮轮系运动方案研究提供参考。

4 结束语

针对齿轮轮系运动方案设计的研究理论体系不完善的问题,笔者运用单元组合方法与实例验证方式,对齿轮轮系运动方案进行了分析;创建了一种轮系运动方案分析模型,通过单元连接方程和单元组合特征状态方程,研究特征状态矩阵分解规则,得到了系统矩阵串联、并联及混联分解算法,实现了特征状态矩阵的拆分,并形成齿轮轮系运动方案分析流程;同时,齿轮轮系的单元库中存在着含传动比、输入转速等设计需求的基本单元,运动特征矩阵进行拆分后,可以通过匹配获取单元并进行组合;最后，通过设计实例对结果进行了验证。

研究结果表明:

(1)齿轮轮系运动方案单元化设计的重点是单元之间的组合,在分析单元组合方式之前必须要研究单元之间的组合约束;

(2)通过分析模型,可以把轮系运动方案求解转变为数学矩阵的计算,并根据状态特征矢量计算规则建立单元组合串联、并联以及混联分解算法;

(3)以齿轮箱为例,阐述不同组合方式下的特征状态方程并获得了9种运动方案,进一步说明本研究中运动方案是高效率且可应用的。

在选择了齿轮轮系的运动方案之后,笔者后续的研究方向是如何确定系统中具体的齿轮参数,比如传动比、配齿数等。