基于EDEM的电磁振动给料机参数研究*

陈亚维,卢坤明,张春明,李 贺

(1.中原工学院 机电学院,河南 郑州 451191;2.郑州东浩科技有限公司 技术部,河南 郑州 451191)

0 引 言

电磁振动给料机(简称:电振机)被广泛应用在冶金、煤炭、电力、化工、建材、轻工和粮食等行业中,与其他设备配套,实现给料、喂料、配料、定量包装和流程自动化作业[1,2]。目前,电振机已经趋于成熟[3],实体产品在市场上也得到了广泛应用。

学者们对电振机做了很多研究:RADEMACHER F J C等[4]采用质点化原理研究了电振机的加料原理;顾平灿[5]从振幅与物料运动方式之间的关系对电振机给料速度进行了研究;柳志康等[6]借助EDEM仿真软件从机械指数和振幅对电振机进行了研究;王新文等[7]基于EDEM对给料机的闸门开度进行了研究;彭美豹等[8]从闸门开度和振幅研究了电振机内物料的定量加料特性;石加联等[9]研究了不同料层厚度下电振机内颗粒的运动规律。

以上研究多是从单个或者两个参数进行研究,而针对参数变化对物料输送速度规律的研究却很少。

本文借助SolidWorks绘制电振机三维模型，用离散元数值软件EDEM,并采用离散单元法[10]、控制变量法系统研究振幅、挡板高度、振动频率、振动方向角这4种参数下的电振机加料规律,通过实验验证挡板高度和振幅变化对电振机加料的影响。

1 电振机加料原理

电振机的结构图如图1所示。

图1 电振机结构图

图1中,电磁铁线圈固定在底座上,通过电磁铁线圈的电流经过半波整流,在正半周内线圈中有电流通过时,衔铁和铁芯相互吸引,这时振动槽向后运动,电振机的前后两块主振板弹簧发生变形,储存一定的势能。在负半周线圈中无电流通过时,电磁铁的电磁力消失,这时板弹簧释放储存的势能,振动槽朝相反的方向运动,推动振动槽中的物料向前运动。当电磁铁线圈持续通电时,电振机就作往复振动,在槽体的连续振动下,物料实现定量输送[11,12]。

2 EDEM仿真

2.1 EDEM模型的建立

除去电振机装置中不必要的部分,笔者利用SolidWorks绘制料仓、挡板、振动槽,并直接在料仓中央位置绘制一个薄板,导入EDEM之后，可以利用该薄板直接建立虚拟颗粒工厂。

导入EDEM之后，电振机计算模型如图2所示。

图2 电振机计算模型

笔者在出口处建立质量流速传感器,来统计实时流速。料槽参数为:长度L=500 mm,振动槽槽宽B=90 mm,槽高H=120 mm,倾斜角度α=0°;料仓底部距离振动槽底部距离90 mm,挡板高度h可以在0～90 mm范围内调节。

2.2 仿真参数的设置

本文采用的豌豆颗粒被近似看作理想球体,且颗粒表面没有黏附力,故笔者选用Hertz-Mindlin[13,14]无滑动模型模拟振动输送过程中颗粒间的相互作用,仿真步长根据瑞利波法确定为Rayleigh[15]时间步长的20%。颗粒工厂先快速生成颗粒,当料仓中存有颗粒后再减缓,根据不同参数下模型的物料输送能力,对颗粒工厂颗粒生成速度进行调节,避免颗粒过多，增加运算时长,也避免颗粒过少出现颗粒不足的现象。笔者设置采样时间0.01 s,仿真时间15 s。

仿真参数设定如表1所示。

表1 仿真参数设定

2.3 仿真设计

该仿真是为了探究电振机在振幅、挡板高度、振动频率、振动方向角度参数下的电振机加料规律。为了减少仿真次数,笔者规定其他参数选用以下参数:振幅A=1 mm,挡板高度h=50 mm,振动频率f=25 Hz,振动方向角β=30°。振幅、频率,均可以在软件中直接进行设置,挡板高度可以通过设置EDEM软件中挡板的CAD参数来调节。振动方向角可以通过调节运动算例始末位置进行模拟。

仿真安排如表2所示。

3 仿真结果与分析

3.1 振幅

在不同振幅下,电振机流速随时间的变化曲线如图3所示。

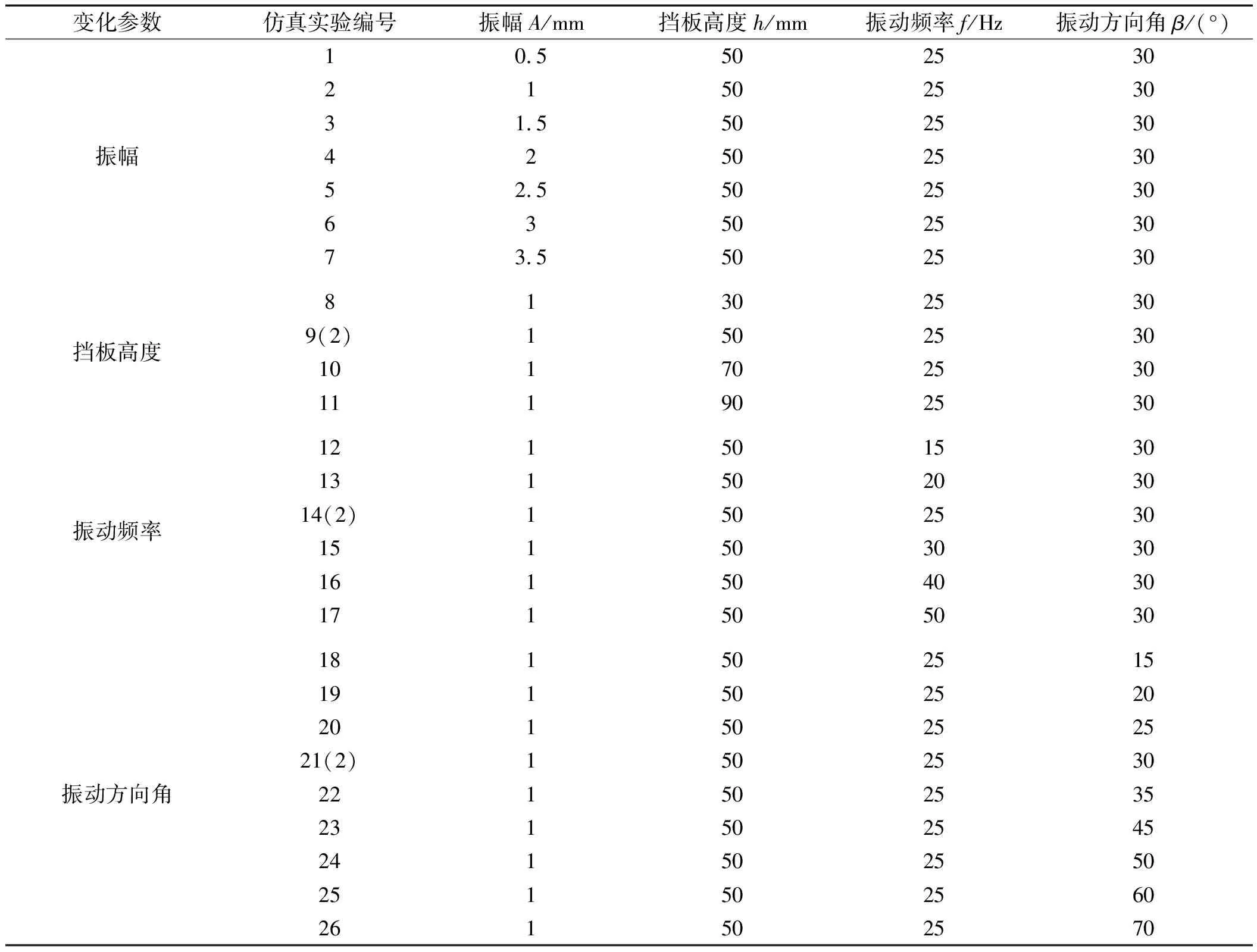
表2 仿真试验

图3 不同振幅下流量随时间变化曲线

由图3可以看出,当振幅在0.5 mm～3.5 mm范围之内时,流速随着振幅的增加而增大;流速达到稳定状态所需的时间随稳态流速的增大而减小。

为了进一步探究振幅与流速的关系,各个振幅流速均达到稳定状态后(8 s以后),笔者取流速平均值绘制流速随振幅的变化曲线,如图4所示。

由图4可以看出,当振幅在0.5 mm～3.5 mm范围内时,电振机的加料速度是随着振幅的增加呈开口向下的二次曲线增长的,曲线拟合的拟合度高达0.995 6。曲线零点解为物料运动所需要的最小振幅。

3.2 挡板高度

在不同挡板高度下,电振机流速随时间的变化曲线如图5所示。

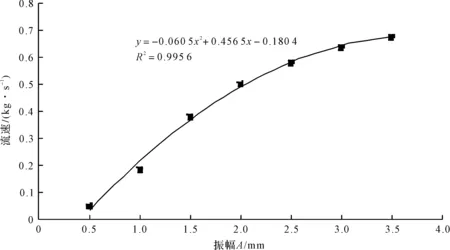
图4 流速随振幅变化曲线图

图5 不同挡板高度下流速随时间的变化曲线

由图5可以看出,流速随着挡板高度的增加而增大。

为了进一步探究挡板高度与流速的关系,当各个挡板高度下流速均达到稳定状态后(8 s以后),笔者取流速平均值绘制流速随挡板高度的变化曲线,如图6所示。

由图6可以看出,电振机的加料速度随着挡板高度的升高呈线性增长,曲线拟合的拟合度高达0.993 5。

3.3 振动频率

在不同振动频率下,电振机流速随时间的变化曲线如图7所示。

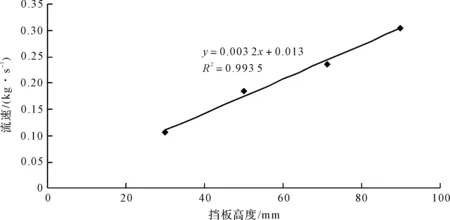
图6 流速随挡板高度的变化曲线图

图7 不同振动频率下流速随时间的变化曲线

由图7可以看出,当振动频率在15 Hz～50 Hz时,流速随着振动频率的增加而增大。

为了进一步探究振动频率与流速的关系,当各个频率下流速均达到稳定状态后(8 s以后),笔者取流速平均值绘制流速随振动频率的变化曲线,如图8所示。

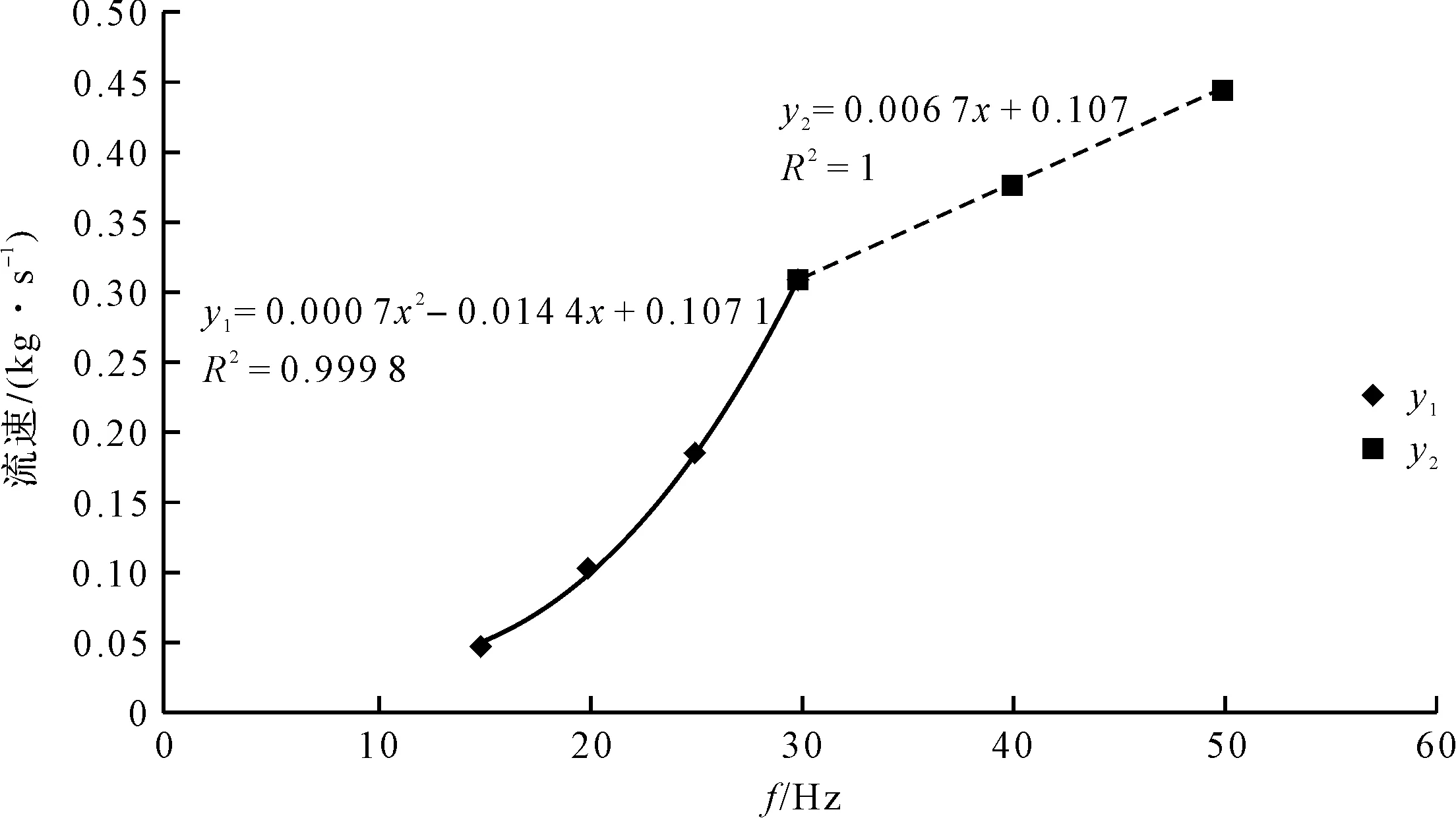
图8 流速随振动频率的变化曲线

由图8可以看出,当振动频率在15 Hz～30 Hz时,电振机的加料速度随着振动频率的增加呈开口向上的二次曲线增长;当振动频率在30 Hz～50 Hz时,流速随着振动频率的增加呈线性增加,曲线拟合度分别为0.999 8和1。

3.4 振动方向角

电振机取不同振动方向角时,流速随时间的变化曲线如图9所示。

由图9可以看出,当振动方向角取15°～45°时,流速随着振动方向角的增加而增大;当振动方向角取45°～70°时,流速随着振动方向角的增加而减小。

为了进一步探究振动方向角与流速的关系,当各个振动方向角下流速均达到稳定状态后(8 s以后),取流速平均值,笔者绘制流速随振动方向角的变化曲线,如图10所示。

图9 不同振动方向角下流速随时间的变化曲线

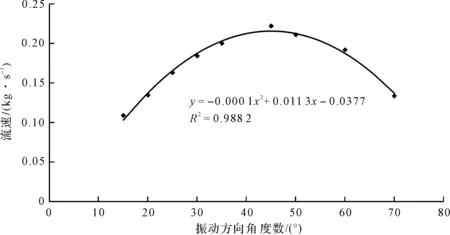
图10 流速随振动方向角度数β的变化曲线

由图10可以看出,当振动方向角在15°～70°时,电振机的加料速度随着振动方向角的变化呈开口向下的二次曲线变化,曲线拟合度为0.998 2。

4 实验验证

实验装置采用郑州艺霖机械设备有限公司的双头定量分装秤,通过调节料仓挡板高度来验证仿真中挡板高度对电振机的影响规律;通过改变创优模块对电振机输入的激振电压来模拟仿真中振幅对电振机的影响规律。由于日常采用AC 220 V电压对设备进行供电,此处经过创优模块对振动电磁铁输入电压进行半波整流,整流后频率为50 Hz恒定不变;设备所采用的电振机振动方向角为20°恒定不变。因此，笔者只研究了振幅和挡板高度对加料速度的影响规律。实验数据通过记录双头秤仪表参数来获取。

双头秤仪表如图11所示。

图11 双头秤仪表

实验并不能直观体现振幅的大小,但对电振机输入不同激振电压时,线圈对衔铁产生的吸引力不同,主振弹簧发生变形量不同,最终反映的振幅不同。所以笔者通过设定目标重量,将中加值设为0,通过采集每次流出物料的实际重量和所用的时间,计算出流速,通过流速的大小,间接反映振幅的大小。

实验分别采集了激振电压为99 V、131 V、164 V、197 V、220 V,挡板高度为50 mm、70 mm、80 mm、90 mm时的流速大小,实验设计如表3所示。

表3 实验验证

机器运行稳定后,每个参数实验5次以上,得到流速随激振电压(振幅)变化曲线如图12所示。

由图12可以看出,当挡板高度一定时,流量均值随着激振电压(振幅)的增加呈二次曲线线性增加。该变化趋势与仿真结果相同。

当激振电压(振幅)一定时,流速随挡板高度增加的变化曲线如图13所示。

由图13可以看出,当激振电压(振幅)一定时,流速随着挡板高度的增加呈线性增长。该变化趋势与仿真结果相同。

图12 不同挡板高度下流速随激振电压(振幅)的变化曲线

图13 不同激振电压下流速随挡板高度的变化曲线

5 结束语

本文借助SolidWorks和EDEM软件,采用离散单元法、控制变量法系统研究了振幅、挡板高度、振动频率、振动方向角4种参数变化对电振机物料输送流速的影响,得出了每一种参数对电振机物料输送流速的影响规律,并通过实验验证挡板高度和振幅变化对电振机加料影响规律的可靠性。研究结论如下:

(1)当振幅在0.5 mm～3.5 mm,激振电压在99 V～220 V范围内时,电振机物料输送流速随着振幅(激振电压)的增加而增加,符合呈开口向下的二次曲线增长规律;

(2)挡板高度在50 mm～90 mm范围内,电振机物料输送流速随挡板高度的增加呈线性增长;

(3)当振动频率在15 Hz～30 Hz时,电振机物料输送流速随着振动频率的增加呈开口向上的二次曲线增长,当振动频率在30 Hz～50 Hz时，流速随振动频率的增加呈线性增长;

(4)电振机物料输送流速随振动方向角的增加先增后减,在45°左右达到峰值,呈开口向下的二次曲线变化规律。

电振机加料流速增大使得其物料输送能力提升,但在一些需要定量加料的场合,不但要求加料速度快,还要求加料的稳定性好;另外,各种参数之间可能会存在交互影响作用。

因此,今后的研究方向主要是探索电振机加料速度与稳定性之间的关系，以及多参数下的综合影响规律。