球墨铸铁磨削表面粗糙度的声发射智能预测研究*

龙 华,朱 奇,郭 力,黄 俊,王 艺

(1.湖南工业职业技术学院 机械工程学院,湖南 长沙 410208;2.复杂薄壁精密零件智能柔性加工技术湖南省工程研究中心,湖南 长沙 410208;3.湖南大学 机械与运载工程学院,湖南 长沙 410082)

0 引 言

汽车发动机的曲轴材料是球墨铸铁QT700-2。曲轴磨削加工质量极大地影响了曲轴的加工质量,也对汽车发动机的性能有非常重要的影响。因此,常使用表面粗糙度评价其磨削加工质量[1]。在曲轴磨削加工时,越早发现表面粗糙度的超差,越能及早地采取相应措施降低损失。表面粗糙度是磨削表面完整性的重要指标,但由于磨削参数、砂轮状态、工件材料及尺寸误差、磨削液、振动等都对磨削表面粗糙度有影响,曲轴磨削表面粗糙度很难准确预测[2]。

PLAZA G等[3]指出,在磨削加工过程中存在大量的声发射(AE)现象。声发射监测是一种无损监测,可以利用声发射技术进行曲轴磨削表面粗糙度在线监测,该技术对于汽车发动机曲轴磨削加工的智能化极其重要。

目前,研究人员针对磨削表面粗糙度的声发射预测已开展了诸多研究。石建[4]利用小波分析提取出了磨削AE信号的特征参数,并将其输入BP神经网络,以判别砂轮的磨损状态;然后将砂轮磨损状态、磨削参数、磨削力比输入BP神经网络,以预测磨削表面粗糙度。REDDY T S等[5]利用加工过程中声发射信号的振铃计数、上升时间以及有效值,预测了加工表面的粗糙度以及砂轮的磨损状态。CHEN X等[6]利用单颗磨粒磨削AE实验,探究了磨削机理,即滑擦、犁耕和切削3个过程中的声发射信号规律。刘贵杰等[7]将AE信号特征作为输入,使用附加动量法优化其神经网络。DIAS E A等[8]结合快速傅里叶变换与小波变换分析AE信号,生成智能信息,开发了一种无心磨削过程中监测其表面质量的工具。胡仲翔等[9]将磨削AE信号中300 kHz～400 kHz频段信号作为学习样本,提取了AE信号特征值输入,使用附加动量方法优化了BP神经网络,以此来预测磨削表面的粗糙度,结果表明其对粗糙度的预测效果较好。熊巍等[10]利用不同频段声发射信号的能量比,来预测磨削表面的粗糙度,并将其应用于铣削过程。郭力等[11]采用遗传算法优化BP神经网络,根据磨削声发射信号均方根和快速傅里叶变换峰值2个特征值,对平面磨削加工中的曲轴(球墨铸铁材料)表面粗糙度进行了较高精度的预测。孙林等[12]利用最小二乘支持向量机表面预测模型,对磨削表面粗糙度进行预测,得到了较高的预测精度。林献坤等[13]以磨削工况参数作为输入,使用支持向量机进行了磨削表面的粗糙度预测。

另外,还有一些基于磨削工况参数的磨削表面粗糙度预测的实验研究。PAN Y等人[14]将磨削加工中的砂轮转速、进给速度以及磨削深度作为BP神经网络的输入,对磨削表面的粗糙度进行了预测。

但是,以往关于磨削表面粗糙度预测的研究中尚存在一些问题:(1)实验数据偏少,磨削声发射信号特征值较少,影响了磨削表面粗糙度预测的可靠性和准确性;(2)一些磨削表面粗糙度预测研究是基于磨削工况参数,不是基于磨削声发射信号,而磨削声发射信号中包含的表面粗糙度信息要比磨削工况参数丰富;(3)一般支持向量机声发射预测磨削表面粗糙度的精度要比BP神经网络高。

因此,本文采用多实验数据、多磨削声发射信号特征值,并且通过优化支持向量机,来对磨削表面的粗糙度进行声发射预测,以提高曲轴磨削表面粗糙度的智能在线监测精度和可靠性。

1 球墨铸铁磨削声发射实验

此处研究的平面磨削声发射实验的曲轴材料是球墨铸铁QT700-2,其工件尺寸为50 mm×20 mm×15 mm;砂轮采用外径200 mm、粒度100#的氧化铝砂轮,砂轮线速度20 m/s。

实验过程中,保持工作台速度不变,仅改变磨削的深度;磨削工件的方向为沿着50 mm×20 mm面的50 mm方向;磨削深度为10 μm、20 μm、30 μm;共测量有200个磨削QT700-2声发射信号和对应的表面粗糙度。

实验中,负责采集磨削声发射信号的是美国物理声学公司PAC生产的PCI-2声发射采集系统;此处设置声发射信号采样频率为2 MHz,设置声发射前置放大增益为40 dB;使用声发射信号的波形流采集功能对原始磨削声发射信号进行完整采集,以对采集到的信号进行后续的分析。

实验中使用光学表面轮廓仪Wyko NT9100对QT700-2工件的磨削表面粗糙度进行测量,测得工件磨削典型表面形貌,即其表面粗糙度。在声发射预测磨削表面粗糙度的研究中,实验测得的200个表面粗糙度值分布范围广泛、均匀[15]14-15。进行磨削表面粗糙度声发射预测模型中,笔者随机挑选训练AE信号数据集和测试AE信号数据集,经多次训练测试,以保证实验数据的无序性;并消除由于训练数据集输入顺序造成的预测结果误差,以保证实验的可靠性。

在磨削表面粗糙度声发射预测中,笔者提取AE信号特征参数作为支持向量回归机(support vector regression,SVR)的输入;同时使用优化算法优化上述支持向量回归机,来提高磨削表面粗糙度预测的精确度。其中的优化算法有遗传算法(GA)和粒子群算法(PSO)。

2 磨削AE信号特征参数

在笔者应用MATLAB软件提取的曲轴材料磨削声发射AE信号的特征参数中,主要包含AE信号时域及频域统计特征参数,如声发射信号波形幅值、均方根值、方差、峰值频率、频谱峰值、功率谱峰值、峭度、偏度、AE信息熵等9个特征值;另外,在AE信号时频域联合分析特征参数中,4个本征模函数IMF(5～8)为磨削AE信号经过经验模态分解(EMD)后,包含了原始磨削AE信号特征频率的4个主分量;分析这4个主分量与原始磨削AE信号的相关性,即可得到IMF(5～8)的相关系数。

笔者选取反映磨削AE信号的9个特征值和这4个相关系数共13个特征参数作为磨削声发射信号数据集的特征参数,并对实验数据集进行归一化操作,以消除计算误差[15]20。

部分磨削AE信号特征参数实验值如表1所示。

表1 部分磨削AE信号特征参数

表1 (续)部分磨削AE信号特征参数

磨削深度为10 μm的磨削声发射原始AE信号以及快速傅里叶变换FFT频谱,如图1所示。

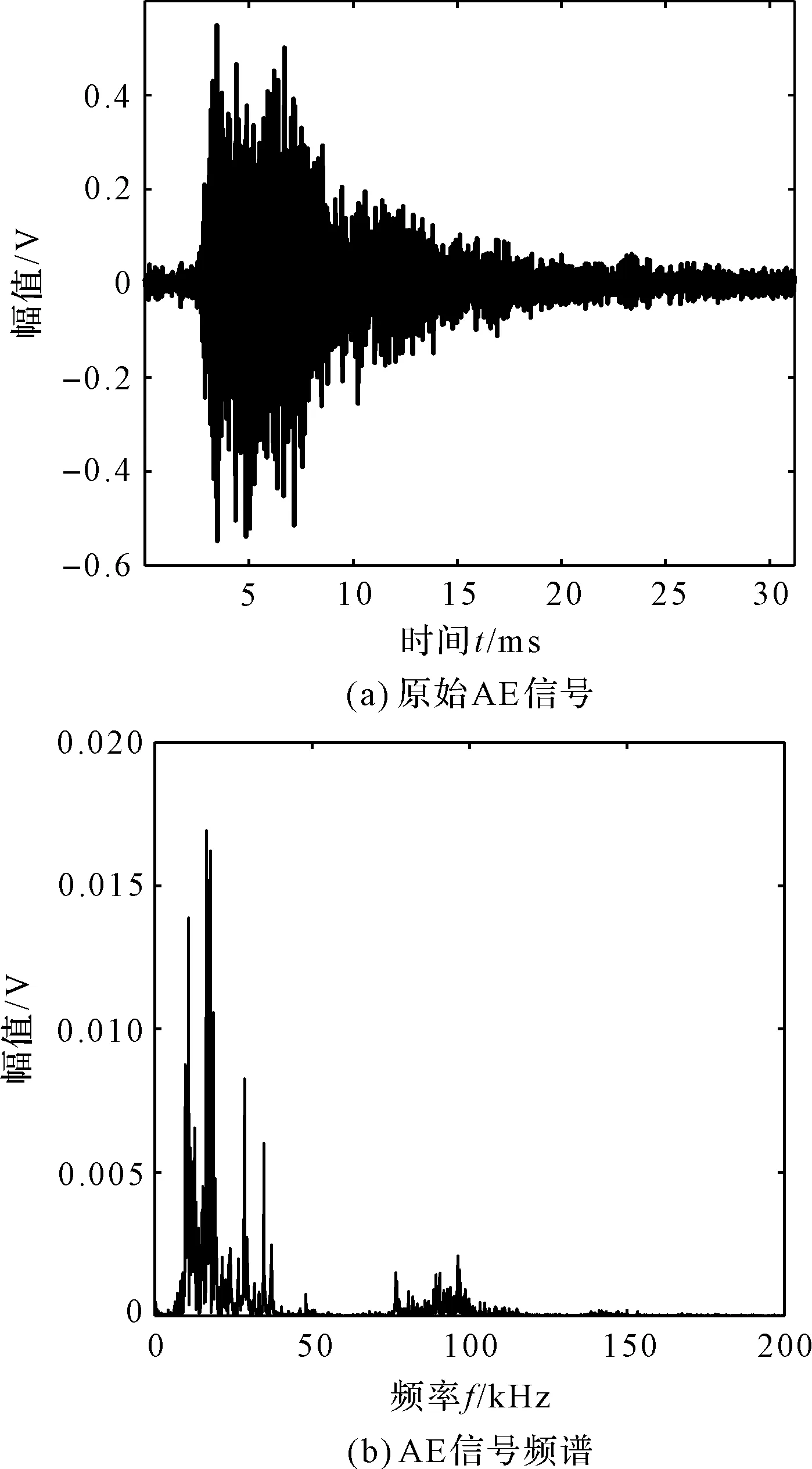
图1 磨削AE信号及其频谱

由图1可以看出:AE信号的能量集中在0～100 kHz频率范围内,且其主要尖峰幅值特征频率分别为11 kHz、17 kHz、34 kHz、56 kHz。

声发射信号经过经验模态分解EMD后的本征模函数IMF(5～8)的频谱,如图2所示。

图2 磨削AE信号的EMD分解主要分量频谱

图2中:分量IMF8的AE信号频谱尖峰频率分别为11 kHz,分量IMF7的AE信号频谱尖峰频率分别为11 kHz、17 kHz,分量IMF6的AE信号频谱尖峰频率分别为11 kHz、17 kHz,分量IMF5的AE信号频谱尖峰频率分别为17 kHz、34 kHz、56 kHz;以上结果与前述磨削AE信号快速傅里叶变换FFT频谱结果相吻合。

在磨削深度增大条件下,磨削声发射信号的频率幅值会随深度的增加而增大,但AE信号频谱尖峰频率变化不明显;且经过EMD分解后,AE信号包含频谱频率尖峰的本征模函数仍为IMF(5～8)。因此,磨削AE信号EMD的本征模函数IMF(5～8)反映了磨削AE信号的主要特征[15]16-17。

定义相对误差RE和均方根误差MSE如下:

(1)

(2)

式中:N—测试集数据的大小;Ra′—磨削表面粗糙度的声发射预测值;Ra—磨削表面粗糙度实际测量值。

此处磨削表面粗糙度声发射试验中获取的样本数量为200组,在支持向量回归机表面粗糙度预测模型的建立过程中,随机选取其中90%的样本180组作为训练集,余下10%的样本20组作为测试集。笔者先利用训练集的180组样本对支持向量回归机进行训练,建立支持向量回归机;再用测试集的20组样本通过支持向量回归机得到20个磨削表面粗糙度预测值,利用式(1,2)可以得到20个磨削表面粗糙度预测集的误差,并将20个表面粗糙度值相对误差的算术平均值,作为本次支持向量回归机预测的单次预测相对误差。

在保持表2中支持向量回归机参数设置不变的情况下,重新按照上述比例,笔者在200组样本中随机选取磨削表面粗糙度声发射信号训练集和预测集,并按照上述步骤完成对支持向量回归机的训练,以及磨削表面粗糙度支持向量回归机测试集的预测。重复上述过程共30次,分别求取这30次预测的单次预测相对误差和均方根误差,并将单次预测相对误差和均方根误差的均值(30次平均相对误差和30次平均均方根误差)作为评价支持向量回归机预测模型的指标。

该方法不仅可以避免支持向量回归机在应用过程中出现的欠拟合(训练误差、测试误差均较大)和过拟合(训练误差仍在减小,测试误差开始增大)带来的结果较差的情况,以及偶然出现的结果极好的情况;同时可以避免选择性使用磨削声发射实验数据给预测结果带来的误差,保证了磨削声发射表面粗糙度预测结果的可靠性。

3 SVR的表面粗糙度AE预测

相对于BP神经网络,支持向量回归机SVR具有一定的优点,其解在理论上是全局最优的,不存在陷入局部最小值陷阱的危险;同时,其实验数据样本少,分析运算的时间短。

笔者采用遗传算法和粒子群算法来优化磨削表面粗糙度声发射支持向量回归机SVR预测模型,两者均通过找到最优参数惩罚参数c、核参数g来优化支持向量回归机。

模型SVR优化算法的参数设置如表2所示[15]27。

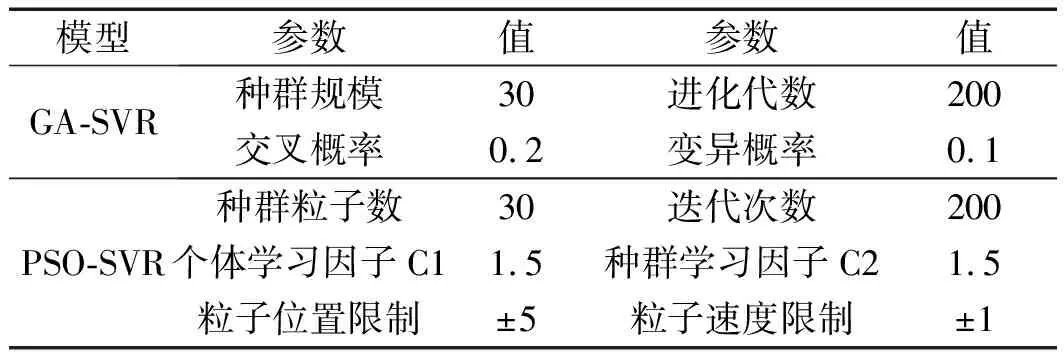
表2 模型SVR优化算法的参数设置

笔者将表1中提取的曲轴材料磨削声发射信号13个特征参数与磨削表面粗糙度一一对应,建立了200组实验数据集,随机选取了其中90%为训练集、10%为测试集,并对数据集进行了归一化操作。适应度函数确定为支持向量回归机SVR预测值的均方差函数。将训练集输入最优解确定的支持向量回归机,进行训练，得到了支持向量回归机预测模型;通过输入实验数据测试集进行磨削表面粗糙度的声发射支持向量回归机预测。

笔者使用表1的曲轴磨削声发射信号特征参数数据集,输入两种优化的支持向量回归机,进行磨削表面粗糙度声发射预测。对两个支持向量回归机预测模型进行30次的磨削表面粗糙度声发射预测做比较评价。

优化SVR的表面粗糙度预测结果如表3所示。

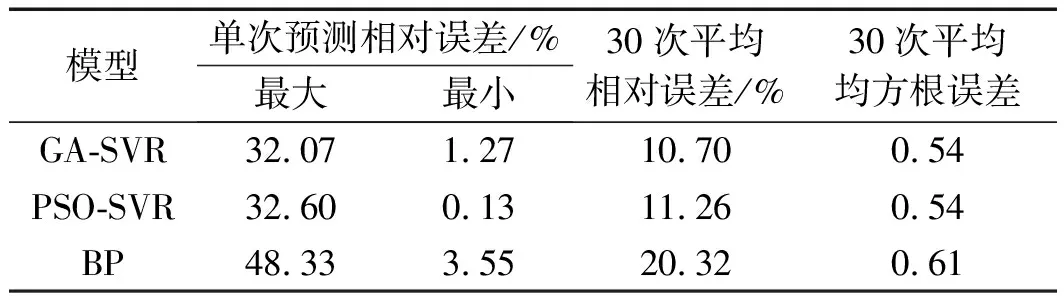
表3 优化SVR的表面粗糙度预测结果

由表3可知:遗传优化GA-SVR得到的优选参数惩罚参数c=1.108 6、核参数g=8.540 2、最优适应度为0.026,磨削表面粗糙度声发射测试集多次平均相对误差为10.70%;粒子群算法优化PSO-SVR得到的优选参数惩罚参数c=1.335 9、核参数g=6.684 3,最优适应度为0.03,磨削表面粗糙度声发射测试集多次平均相对误差为11.26%;两者的适应度曲线均收敛,两种优化算法支持向量回归机SVR预测模型得到的磨削表面粗糙度预测结果相差较小。

对比表3中的BP神经网络,磨削表面粗糙度声发射预测模型多次平均相对误差为20.32%[15]25-28,可见支持向量回归机磨削表面粗糙度声发射预测模型的误差较小、准确度较高。

4 结束语

针对磨削表面粗糙度声发射预测精度和可靠性较低的问题,笔者采用多实验数据、多磨削声发射信号特征值,并且通过优化支持向量机,来对磨削表面的粗糙度进行声发射预测,提高了曲轴磨削表面粗糙度的智能在线监测精度和可靠性。

笔者展开了研究工作并得到了相关结论:

(1)获得了200组磨削表面粗糙度声发射实验数据,提取了包含磨削声发射信号EMD分解的4个本征模函数相关系数在内的13个特征参数;建立了遗传算法优化的支持向量回归机GA-SVR、粒子群算法优化的支持向量回归机PSO-SVR;

(2)随机在200组实验数据中,提取了13个磨削声发射信号特征参数,输入到2个预测模型中,反复进行了训练和预测,提高了其可靠性,较BP神经网络,支持向量回归机GA-SVR和PSO-SVR的磨削表面粗糙度声发射预测精度有明显提高。

在后续的研究中,笔者将进行磨削声发射在线监测汽车发动机曲轴磨削表面粗糙度的研究。