圆柱齿轮刮齿加工中的高效切削力预测方法研究*

彭桂枝,李国庆

(1.江阴职业技术学院 机电工程系,江苏 江阴 214405;2.江苏理工学院 汽车与交通工程学院,江苏 常州 213001)

0 引 言

不同于传统的滚齿和插齿加工,数控强力刮齿加工是一种高速通用齿轮加工方法,可以进行内齿轮、外齿轮、直齿轮或斜齿轮的加工,且加工时间较短。随着数控技术的不断进步,刀具寿命、振动和伺服同步等过去阻碍其推广的问题,在近几年逐渐被克服,使得强力刮齿加工技术[1-3]开始受到齿轮加工行业的极大关注。

然而,由于数控强力刮齿加工过程中存在着的几何和运动学复杂性,给其分析建模和仿真带来了较大的挑战性。GUO E等人[4]对强力刮齿刀具的设计问题进行了研究,并提出了一种简化的合力仿真计算方法;TACHIKAWA T等人[5]将归一化切削力的谐波分量与过程切削速度相关联,提出了一种可避免结构振动的建模方法;为了处理几何学和运动学的复杂性,KLOCKE F等人[6]采用了一种平面交点的方法,来数值逼近每个时间步长的刀具-工件啮合。

近期,TAPOGLOU N等人[7]使用基于CAD的仿真模型来计算强力刮齿中的未变形切屑和齿轮几何。虽然该方法在切削力预测的精度方面能够满足需求,但是每次预测均需要重新校准切削系数,且该方法所需的计算量较大。

因此,笔者采用dexel离散几何建模方法,设计出一种新颖的强力刮齿切削力预测方法,构建圆柱齿轮强力刮齿的运动学模型,并将其应用于基于dexel的实体造型[8]中,将二维切屑形状与斜角切削模型相结合,来预测每个时间步长的切削力;为了提高其仿真效率,采用部分工件建模和叠加来估算整个过程的切削力;最后通过强力刮齿实验,以验证该预测方法的可行性和有效性。

1 强力刮齿运动学模型

以直齿圆柱齿轮为例,强力刮齿的运动学模型如图1所示。

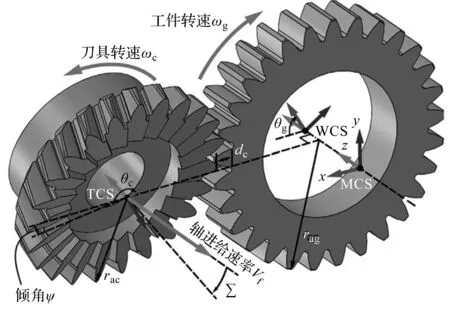
图1 强力刮齿的运动学模型

图1中,刀具围绕机床坐标系(machine coordinate system, MCS)的x轴以交叉轴角∑定向。当刀具沿工件的z轴方向以恒速vf轴向进给时,刀具和工件之间通过相对旋转,完成切削运动;在每一次加工过程中,刀具以指定的深度dc径向定位到工件中。围绕MCS的y轴定义的倾角ψ也可以应用于刀具,用于齿形修整或提供额外的间隙。

由于刀具的旋转速度是基于刀具-工件齿轮比而建立的,该齿轮比是齿轮齿数和刀具齿数的函数。

对于具有类似运动的斜齿轮而言,根据刀具的节圆半径和轴向进给速度,其所需的螺旋角会产生额外的旋转项,即:

(1)

式中:ωc—刀具的转速;ωg—工件的转速;Ng—齿轮齿数;Nc—刀具齿数;βg—齿轮螺旋角;rpc—刀具节圆半径;vf—刀具沿工件z轴轴向进给的速率。

为了与刀具-工件啮合计算所需的dexel模型兼容,有必要在工件坐标系[9](workpiece coordinate system, WCS)中建立强力刮齿运动学模型。

由于刀具几何形状是在刀具坐标系(tool coordinate system, TCS)中定义的,此处应用了齐次变换的乘积,包括单个旋转R和平移T,如下所示:

(2)

式中:Rz,-θg—齿轮绕其z轴反向旋转θg;Rz,θc—齿轮绕其z轴旋转θc;Tg→c—MCS中从工件到刀具的平移;Tc→racRy,ψTrac→c—刀具按照角度ψ的倾斜。

在工业实践中,通常将切削速度定义为vc≅ωcrpc。然而,实际切削速度的大小和方向会在刀刃上表现出明显的变化,从而导致其局部倾斜的接触条件不断变化。因此,需要精确求解切削速度矢量。

对于刮刀上的给定点P,其位置为rP/c(相对于刀具)和rP/g(相对于工件),可以使用速度矢量在WCS或TCS中找到真实切削速度,即:

vc=wc×rP/c-wg×rP/g+vf

(3)

式中:wc—刀具的转速矢量;wg—工件的转速矢量;vf—刀具沿工件z轴轴向进给的速度矢量。

2 强力刮齿预测方法

2.1 未变形切屑形状预测

笔者采用基于dexel的实体造型系统(ModuleWorks)对所设计强力刮齿运动学模型进行了实现。工件由平行线段阵列表示,这些线段的起点和终点描述了材料的外表面。

刀具形状用三角面网格来描述,刮刀的三角形网格表示及其切削形状如图2所示。

图2 刮刀的三角形网格表示及其切削形状

笔者通过定义刀具相对于工件的位置和方向(姿势),以离散的时间步长执行切削;在当前工件的每个时间步长中,对扫描的切削体积进行布尔相减,生成更新的工件几何形状。

基于WCS的dexel强力刮齿仿真如图3所示。

图3 基于WCS的dexel强力刮齿仿真

从以dexel表示的CWE中提取二维切屑形状的方法,如图4所示。

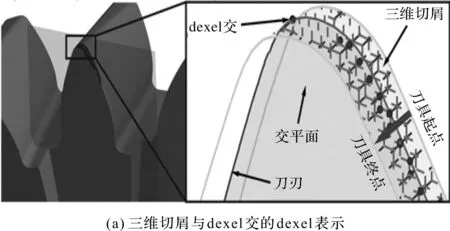
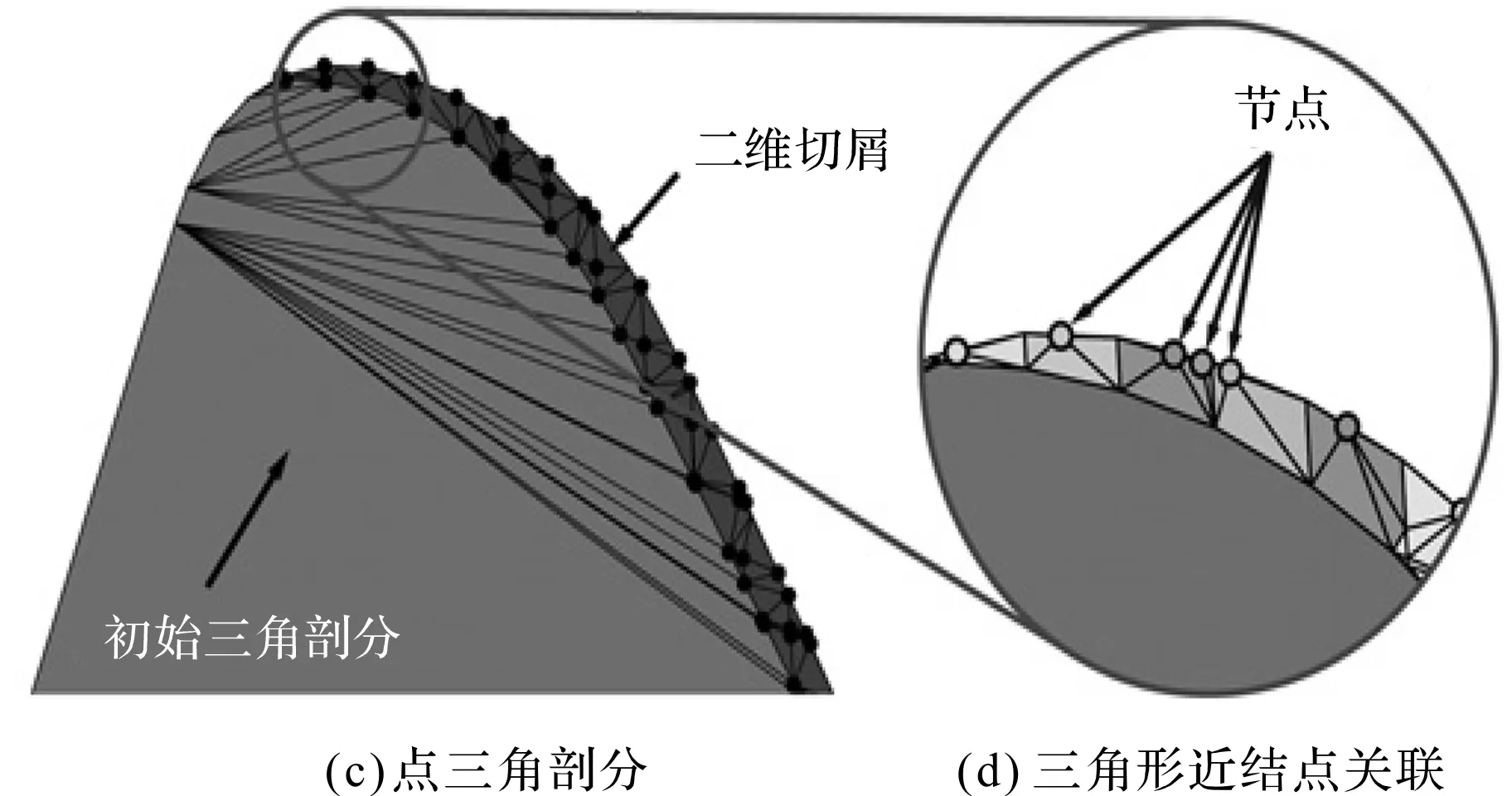
图4 从以dexel表示的CWE中提取二维切屑形状的方法

图4中,三维未变形切屑形状的dexel表示用于构建二维切屑横截面;笔者通过连接平行dexel的端点来估计切屑三维边界,有效地在dexel数据的每个xy、xz和yz平面周围创建轮廓;然后,轮廓与刮刀的平面或圆锥前刀面相交,产生切屑横截面的二维点云。

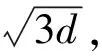
刀具刃口被离散为多个点(称为节点),这些点是在半时间步长时,刀具姿势处定义的。然后,笔者将切屑形状的三角形与最近的节点关联,每个三角形的几何形状用于计算其关联节点的局部切屑面积a;最后,在每个节点上应用斜切削力模型,以获得每个时间步长的切削力预测。

2.2 切削力计算

本文将二维切屑形状与斜角切削模型[11]相结合,以预测每个时间步长的切削力[12]。对于与切屑形状相关的每个节点,在切向t、进给f和径向r方向上产生的力增量分量Ft、Ff和Fr分别可以表示为:

Ft=Ktca+Kteb,Ff=Kfcafc+Kfeb,Fr=Krca+Kreb

(4)

式中:Ktc,Kfc,Krc,Kte,Kfe,Kre—通过试验确定的切削力系数。

切向t、进给f和径向r方向的矢量必须在TCS中解析,以便正确定位式(4)中它们对应的力分量。这是通过考虑每个节点的局部几何形状和切削运动学来实现的,具体遵循文献[13]中详细描述的刨齿操作过程,该方法适用于强力刮齿。

用于刀刃的斜角切削模型如图5所示。

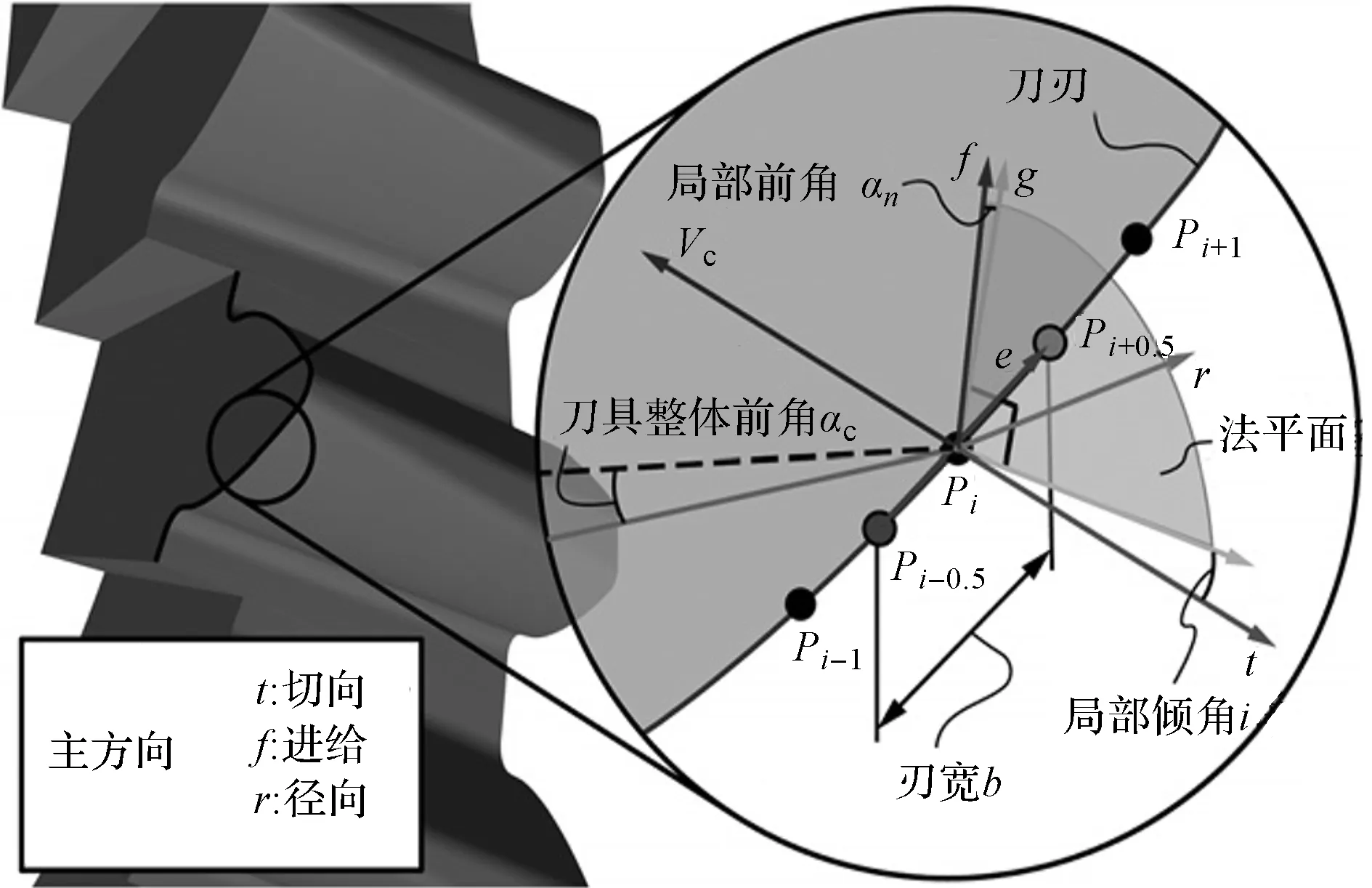
图5 用于刀刃的斜角切削模型

该过程考虑了刀具的整体前角αc、局部刀刃形状(Pi-1,Pi,Pi+1)和每个节点处的切削速度矢量vc,还计算了刀刃上任意点的有效局部前角αn和倾角i。

将计算出的切削力方向矢量与式(4)中的力大小相结合,可获得每个节点的切削力矢量;合并来自当前时间步长的所有参与节点的力矢量,从而预测其瞬时总切削力。

2.3 通过叠加提高仿真效率

CWE计算是仿真中计算量最大的任务。因此,为了提高仿真效率,本文提出只对部分工件进行建模,并通过叠加切削一个齿隙所需的力,来估算整个过程的切削力。

用于减少CWE计算时间的部分工件如图6所示。

通过部分工件仿真重建y轴切削力的方法如图7所示。

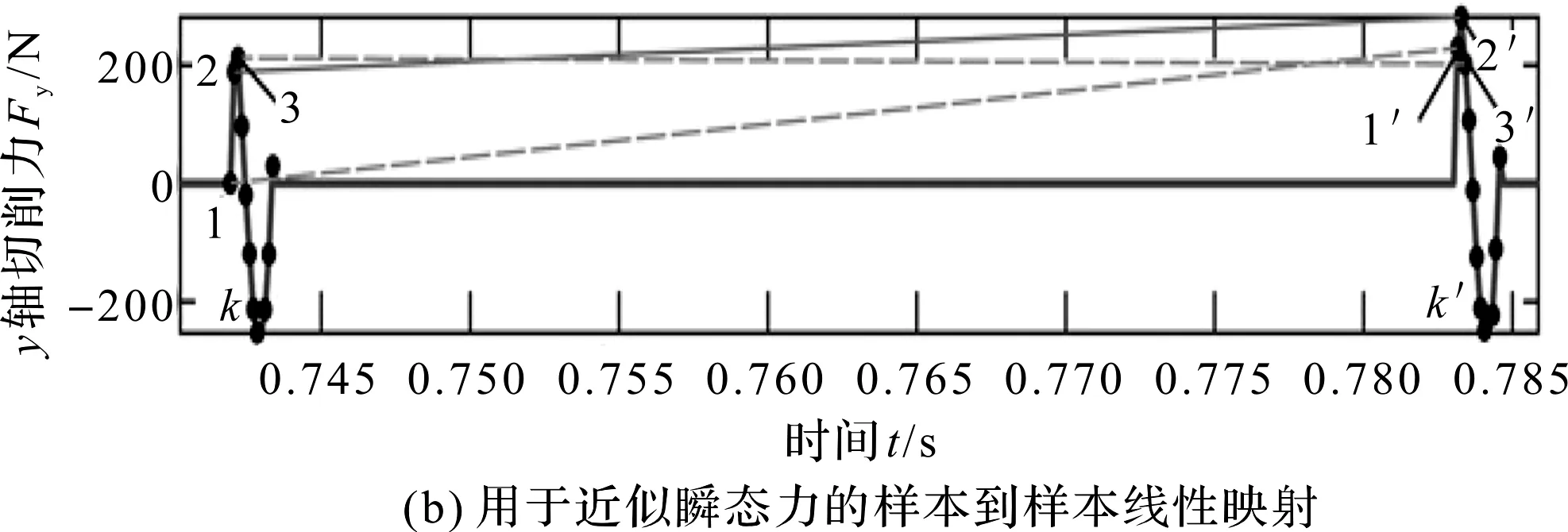
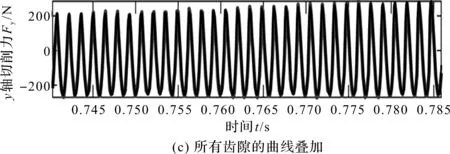
图7 通过部分工件仿真重建y轴切削力

图7(a)中,切削该齿隙的CWE和力曲线预测计算,是在多个由齿轮旋转周期tg=60/(2πωg)隔开的刀刃行程中完成的。

图7(b)中,由于逐渐变化的啮合条件,本文采用连续力曲线之间样本到样本的线性映射,来捕获影响切削力的瞬态效应。

图7(b)对应图7(a)中缩放窗口,覆盖单个齿轮的旋转周期。该映射用于正确缩放和调节来自剩余Ng-1齿隙加工的期望作用力,刀刃的通过周期tp=60/(2πωcNc);最后,通过叠加每个齿间隙加工时预测的各个力曲线,估算出图7(c)中MCS中的总力。

由于本文没有通过整个工件形状来预测切削力,而是采用部分工件仿真法,笔者将仿真时间进行有效缩短,可以大大提升其计算的效率。

3 实验与结果分析

在德马吉NT5400DCG车铣床上,笔者对所提的强力刮齿预测方法进行验证。

其中,切削力的测量是通过德国SPIKE无线传感刀具夹头来进行的[14]。该夹头使用位于不同位置和方向的多个应变片进行应变分析,并融合传感器以产生轴向力、扭矩和弯矩数据;采样频率为2.5 kHz,刀刃的通过频率(1/tp)为322.38 Hz。

该测量实验装置的实物图如图8所示。

图8 测量实验装置

该测量实验装置中,刀具为AlCrN涂层高速钢刮削刀,工件材料为AISI4340钢。

工件和刀具参数如表1所示。

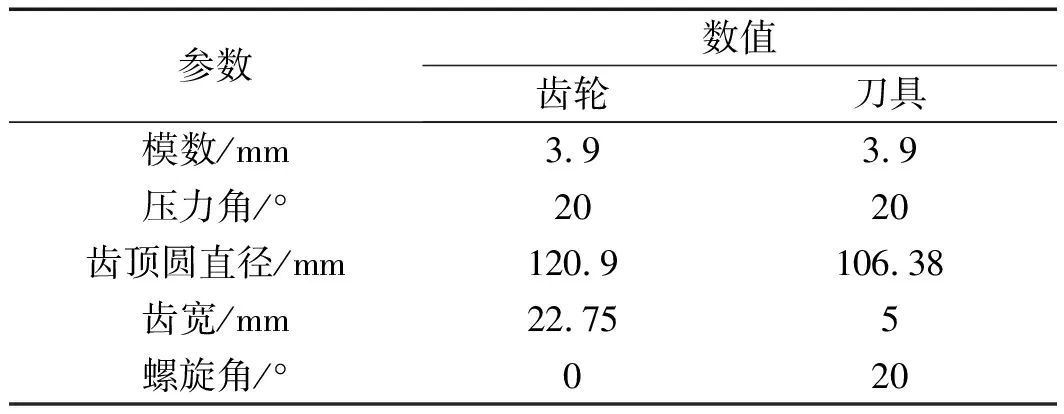
表1 工件和刀具参数

验证试验中的加工条件如表2所示。

表2 验证试验中的加工条件

在仿真过程中,笔者利用CutPro加工仿真软件中适用于AISI4340的Kienzle切削力模型[15,16],并根据有效的局部前角αn和倾角i,计算出了每个切削节点的系数Ktc、Kfc、Krc。

笔者使用具有通带频率fp=1/tp+1/tg+5 Hz和阻带频率fs=1/tp+1/tg+10 Hz的切比雪夫低通滤波器,对x和y轴上SPIKE刀具夹头的数据进行了滤波,使用采样窗口大小为10tp的移动平均滤波器对z轴数据进行了滤波。

笔者将采用该方法所获得的预测结果与TCS中的测量结果进行了比较,其对比结果如图9所示。

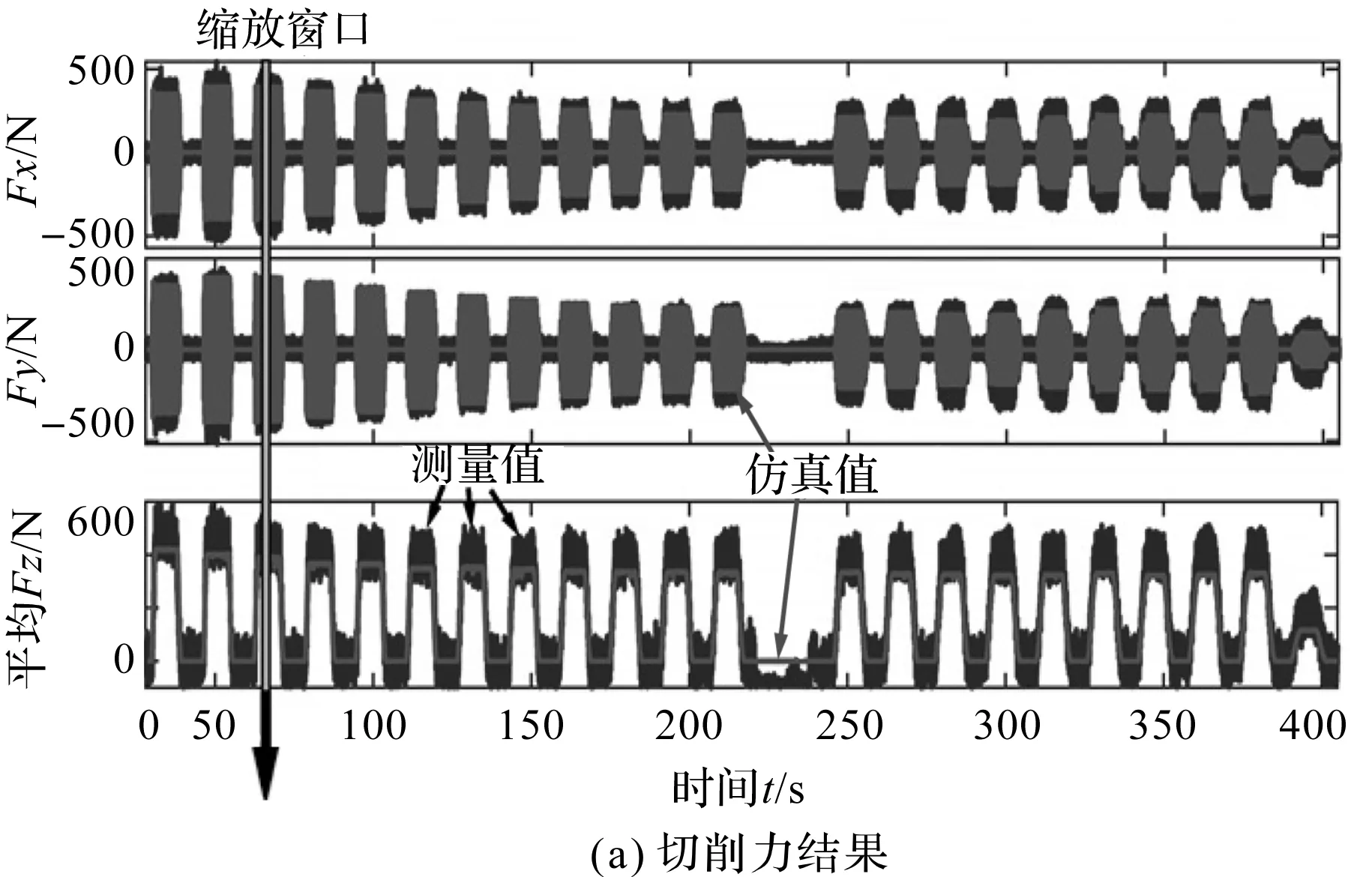
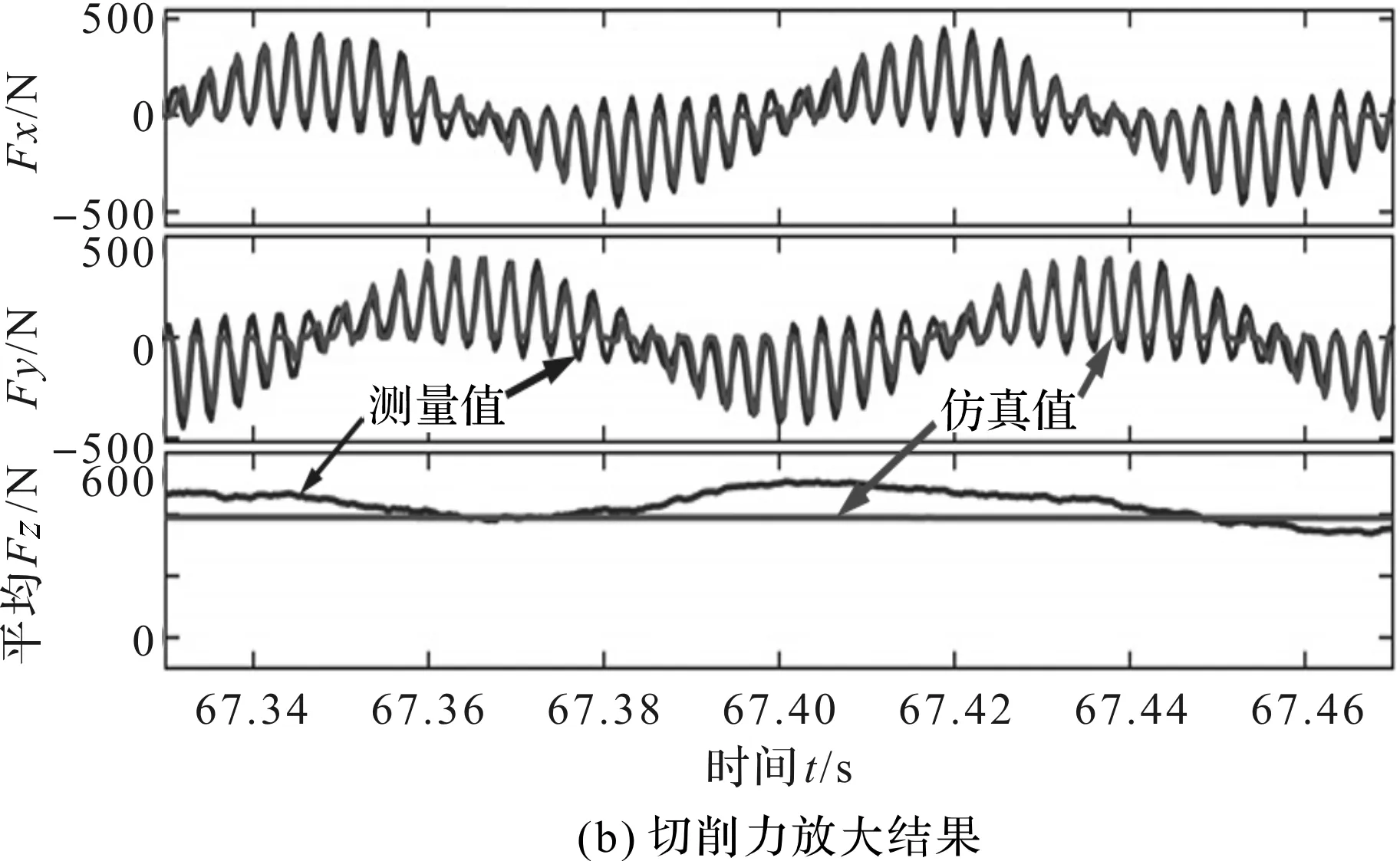
图9 切削力验证对比结果

从图9可以看出:笔者所提的强力刮齿预测方法x、y轴的切削力预测结果与测量结果几乎完全一致,z轴上结果也差别较小,可以准确地预测切削力;该方法无需重新校准切削系数,简化了切削力预测的复杂度。

此外,在相同实验条件下,笔者将所提的强力刮齿预测方法与TAPOGLOU等人所提的基于CAD仿真模型的强力刮齿预测方法进行了对比。

两种方法的切削力预测性能对比如表3所示。

表3 两种方法的切削力预测性能对比

表3中,均方根(root mean square, RMS)误差是以每个轴上的峰值切削力(x:544.3 N;y:443.5 N;z:605.9 N)进行归一化表示的结果。

从表3可以看出,相比与基于CAD仿真模型的预测方法,笔者所提预测方法的RMS误差平均降低了7 N,切削力预测准确率提升了约9.7%。

4 结束语

在数控强力刮齿加工过程中,因采用建模和有限元仿真计算其切削力较为耗时、复杂,为了解决这一个问题,笔者基于dexel离散几何建模,提出了一种用于预测强力刮齿加工中切削力的新方法,并在切削试验中对该方法的使用效果进行了验证。

研究结果表明:

(1)与现有方法相比,采用部分工件仿真结合叠加法,提升了计算效率;

(2)在不重新校准切削系数的情况下,x、y轴和z轴上的切削力预测结果与测量结果非常吻合;

(3)切削力预测RMS误差平均降低了7 N,即准确率提升了约9.7%;该结果为进一步预防刀刃的早期疲劳破坏,优化强力刮齿工艺参数提供了更加精确的理论依据。

然而,目前该方法还存在不能仿真工具/工件振动的局限性。因此,在后续的工作中,笔者将针对该问题开展进一步的研究,并测试不同工艺参数组合对其的影响。