转台齿轮传动系统的误差建模及其精度分配研究*

熊奉奎,张 明,袁越锦,付军豪,刘 康

(1.陕西科技大学 机电工程学院,陕西 西安 710016;2.绵阳职业技术学院,四川 绵阳 621000;3.四川轻化工大学,四川 自贡 643000)

0 引 言

齿轮传动是现代机械工业中核心的传动机构,因此,对齿轮传动系统进行传动误差建模计算及精度分配,无疑也就成为了对现代机械进行优化设计的关键[1]。

在齿轮传动系统传动误差建模计算上,大连理工大学的张凯[2]提出了针对直齿圆柱齿轮传动系统的弹性误差运动模型,揭示了直齿齿轮传动系统误差与各零件的几何误差、弹性变形之间的内在联系;但其未对斜齿齿轮进行探究。王保民等人[3]综合考虑了影响齿轮副传动误差的转角偏差与装配偏心误差,建立了切向综合公差与输出齿轮的最大角度误差的关系式,及法向侧隙与空间回转角的关系式。王朝兵等人[4]针对行星齿轮系,将各齿轮的齿距偏差及偏心误差等随机误差映射到哨合线上,建立了多级传动误差刚性亲合模型,并结合蒙特卡洛法,剥离出了对传动误差影响最大的随机误差;但其未对传动误差进行系统的数学建模计算。

在齿轮传动系统精度分配上,传统精度分配均建立在确定的精度分配原则和方法上,例如相似原则、等公差原则、等影响原则、成比例影响原则、等精度原则等[5]。然而，在实际生产中,上述方法普遍存在没有与齿轮的具体结构特征相结合的问题,例如:齿轮的尺寸大小、齿距累计误差、齿轮轴向跳动误差等特征。故采用上述传统精度分配方法对齿轮传动系统进行精度分配,在实际生产时还需人为进行调整、搭配,反复核算和试验,不具备良好的自适应性及鲁棒性[6]。

本文以新型航发叶片加工五轴机床转台[7]26为例,先建立从单个齿轮到一对齿轮，再到齿轮传动系统的分步误差计算方法;进而建立以概率统计法为基础的传动误差数学模型,对传动误差进行计算;然后再建立基于多目标优化遗传算法的传动精度分配方案,对传动系统的齿轮精度进行分配;最后将两者结合使用,得到一个传动系统优化设计方案,并通过实验对优化设计方案进行验证。

1 转台齿轮传动系统传动误差分析

1.1 新型转台结构简介

新型转台传动系统结构形式如图1所示。

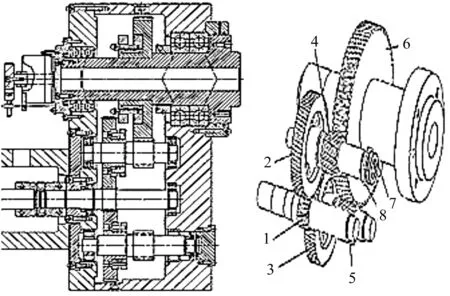
图1 转台传动结构1—主动齿轮轴;2,3—斜齿轮;4,5—中间齿轮轴;6—输出轴斜齿轮;7—推力球轴承;8—开槽碟簧

齿轮传动系统工作原理为:

在装配时扭转调节从动斜齿轮2与斜齿轮轴4的相对角度位置,同时以相同的方法调节从动斜齿轮3与斜齿轮轴5的相对角度位置,以保证主动斜齿轮轴1同一个齿的正反两面分别和从动斜齿轮2和3的对应齿的反正两面紧密啮合,而斜齿轮2和3的啮合齿的另外两个齿面则和斜齿轮轴1的齿面留有较大间隙,而不能形成有效啮合;

同时,输出轴上的斜齿轮6和斜齿轮轴4和5也以同样的原理相啮合,最终保证输入斜齿轮轴1进行正反转切换时,分别从相异的传动链传递运动和扭矩;而另一条非工作传动链总是做随动运动,且不产生运动干涉,从而达到消除正反转切换误差的目的[7]27。

1.2 单个齿轮传动误差的影响因素分解

传动误差是指在齿轮传动系统中,瞬时速比对理想速比的偏差,其最终导致读数齿轮的实际转角偏离理论转角[8]。因此,新型转台的传动误差可以认为是,输出齿轮6的实际转角位置相对理想转角位置的偏差。大量研究表明,传动误差由固有位置误差、装置误差及工作过程中的形变误差3部分组成[9]。

1.2.1 齿轮固有位置误差

齿轮固有位置误差来自齿与齿的位置误差和齿轮旋转位置误差的综合作用[10],主要源于齿轮的加工过程。

齿与齿的位置误差是实际齿廓对理想齿廓的偏离,影响齿与齿的位置误差的主要因素是基节误差和齿形误差,也可以叫做齿轮的大周期误差。

齿轮旋转位置误差主要是由于几何偏心(齿轮实际旋转中心对理论旋转中心的轴线偏离距离)和运动偏心(齿廓相对理论位置产生切向位移和歪斜)造成的正弦位置误差,其总是在齿轮转动时随转角θ做正弦变化,也可以叫做齿轮的小周期误差[11]421。

综上所述,齿轮的固有位置误差主要由基节误差、齿形误差、几何偏心、运动偏心4个误差因素组成。这些误差因素综合后造成齿轮的回转中心产生偏移,形成齿轮的综合偏心误差e[11]421。

齿轮的综合偏心误差e对齿轮传动误差的影响如图2所示。

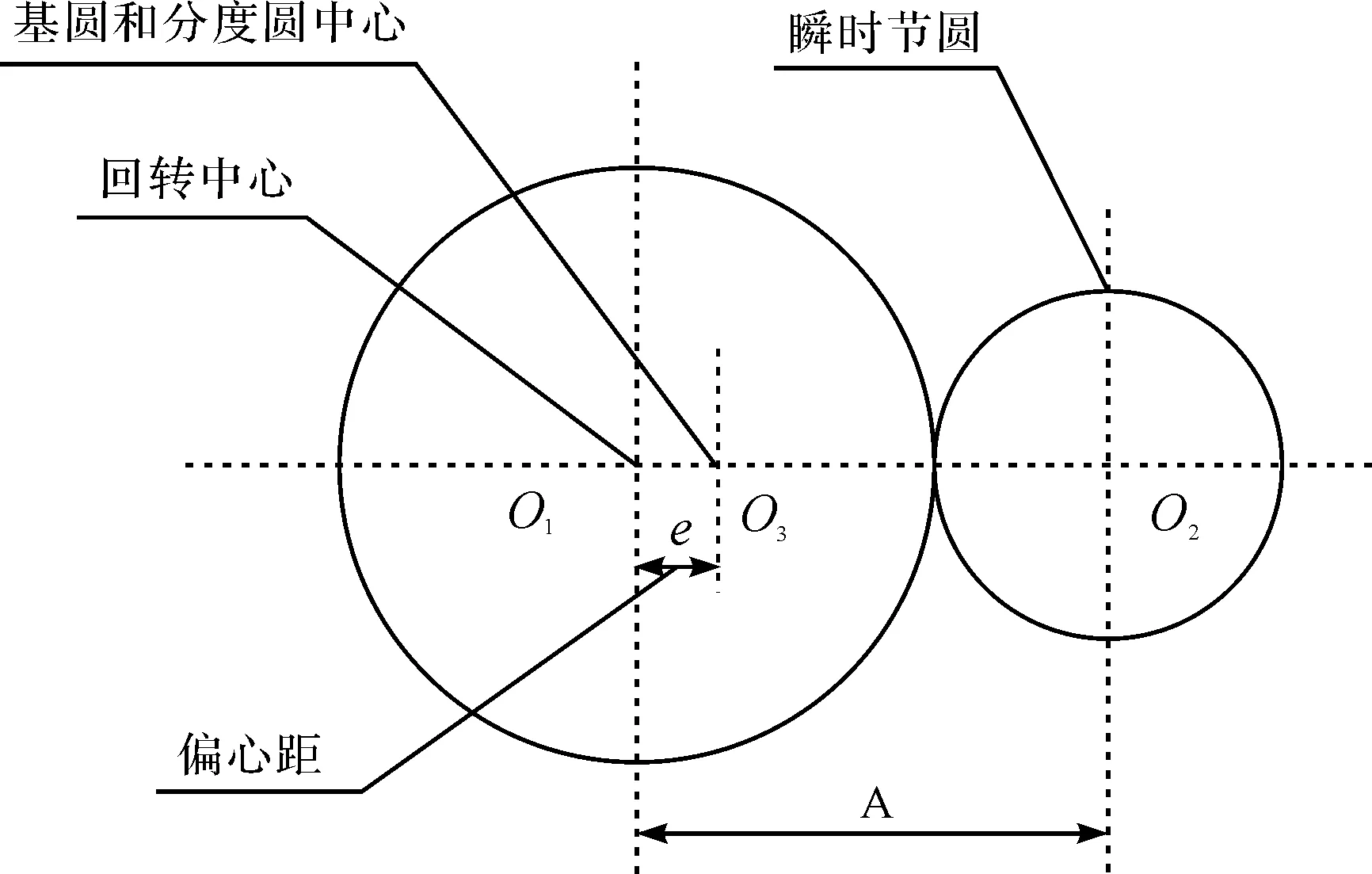
图2 综合偏心误差对传动误差的影响

由图2可得,假设主动齿轮1沿逆时针方向转动,则从动齿轮2沿顺时针方向转动,当齿轮1的回转中心产生一个e的偏心量时,齿轮固有位置误差为[12]:

(1)

式中:Δ1—齿轮固有位置误差;e1—主动齿轮的偏心距;φ1—齿轮的偏心距与回转中心之间o1o2的夹角;αn—斜齿轮的压力角;esinφ1—偏心距产生的传动误差;ecosφ1tanαn—从动齿轮产生的传动误差。

齿轮的固有位置误差为:

(2)

由式(2)可知,齿轮的偏心距e引起的齿轮传动误差Δ1符合三角正弦函数变化规律。

(3)

1.2.2 装置误差

在转台实际运转的过程中,齿轮2的转动中心位置无疑非常重要[13]。装置误差是齿轮2实际转动中心对理论转动中心的偏离,相当于齿轮2发生了几何偏心。装置误差由齿轮孔与轴颈间的间隙Δe2、齿轮安装处轴颈的径向跳动Δe3和轴承的径向跳动Δe4组成[7]28。

3个误差对齿轮传动误差的影响的分析方法与齿轮偏心造成的传动误差分析方法一致,其计算公式为:

(1)齿轮孔与轴间的间隙偏心e2导致的传动误差Δ2:

(4)

(2)轴颈的径向跳动偏心e3导致的传动误差Δ3:

(5)

(3)轴承的径向跳动偏心e4导致的传动误差Δ4:

(6)

(4)齿轮孔与轴之间的间隙Δe2与偏心e2的关系为:

(7)

(5)轴颈的径向跳动Δe3与偏心e3的关系为:

(8)

(6)轴承的径向跳动Δe4与偏心e4的关系为:

(9)

式中:Δei—齿轮的各跳动量,均服从正态分布;φi—齿轮的各跳动量对应的相位角,均在区间[0,2π]上服从均匀分布。

1.2.3 工作过程中的形变误差

在转台传动系统工作过程中,齿轮会受到间歇性随机载荷作用,从而产生变形,最终映射到齿轮的传动误差上(即变形误差)。变形误差主要是来源于磨损误差、塑性变形误差、弹性变形误差、热误差及疲劳变形误差。而塑性变形和疲劳破坏,均属于齿轮典型的失效形式之一,不在误差的研究范围之内。

而对于斜齿轮变形(磨损)的误差补偿,此处笔者采用了非标碟簧开槽随动补偿机构予以补偿,并在笔者已发表的论文《新型转台开槽碟簧随动补偿磨损误差机构设计》中有详细分析。

1.3 转台齿轮传动系统传动误差分析

1.3.1 单个齿轮传动误差

由误差独立作用原理可得,单个齿轮的误差是由齿轮的固有位置误差和装置误差组合得到的。由参考文献[7]得,单个齿轮的传动误差ΔE的计算公式为:

ΔE=Δ1+Δ2+Δ3+Δ4

(10)

1.3.2 一对齿轮副的传动误差

一对齿轮副的传动误差则是由两个互相啮合的齿轮的传动误差组合而成,由读数法可得其计算公式为:

(11)

式中:Δθf—齿轮副的传动误差;ΔE1，ΔE2—分别为主动齿轮和从动齿轮的传动误差;R2—从动齿轮的分度圆半径。

1.3.3 齿轮传动系统的传动误差

将齿轮传动系统中所有齿轮副的传动误差合理地累加到读数齿轮上,就能得到齿轮传动系统的整体传动误差。如果取第n轴为读数齿轮轴,则齿轮传动系统的整体传动误差的计算公式为[7]29:

(12)

式中:Δθfn—第n对齿轮副的传动误差;in—第n对齿轮副上n轴到n+1轴的传动比。

对于新型转台而言,参考式(12),并以齿轮6为读数齿轮,转台传动系统的传动误差为:

(13)

式中:Δθf1—齿轮1与2的啮合传动误差;Δθf2—齿轮4与6的啮合传动误差;i2—齿轮4与6的传动比。

2 转台传动系统传动误差建模计算

由1.2节可推得,组成传动误差的各个误差因素均为随机变量,因此传动误差也一定为随机变量,最后计算齿轮传动误差时,就难免需要考虑各误差因素的均值μ和方差D。以概率统计法为基础,笔者采用数学建模的方法,对传动误差进行计算。

(14)

(15)

其中,齿轮孔与轴之间的间隙偏心e2服从瑞利分布,相位角服从在[0,2π]区间的均匀分布。

由概率论可知:

(16)

(17)

又因为Δe2服从正态分布,所以标准差为:

(18)

由于随机变量e2和φ2是互相独立的,有:

(19)

又因为:E[sin(φ2+αn)]=0,所以有:

μ2=0

(20)

装置误差中,各间隙Δei均服从正态分布,所以齿轮安装处轴颈的径向跳动偏心e3和轴承的径向跳动偏心e4所引起的传动误差Δ3,Δ4的均值和方差分别为[14]2912:

μ3=0

(21)

μ4=0

(22)

一对齿轮的传动误差的均值和标准差为:

μ1,2=0

(23)

齿轮传动系统的传动误差也服从正态分布,若分布范围取6σ1,2,则传动误差的极值为:

(24)

相应角传动误差Δφ1,2的均值和标准差分别为:

μφ1,2=0

(25)

式中:mn—法向模数;z2—从动轮齿数。

综合式(14～25)得,一对齿轮的角传动误差为:

(26)

式中:F′i1,F′i2—主动轮和从动轮的切向综合误差;Δe21,Δe22—主动轮和从动轮的孔与轴间的间隙;Δe31,Δe32—主动轮和从动轮的安装处轴颈径向跳动误差;Δe41,Δe42—主动轮和从动轮的轴承径向游隙。

根据式(25,26),并结合读数法,可得转台传动系统的传动误差计算模型为:

(27)

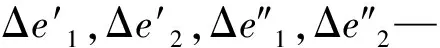
3 转台齿轮传动系统的精度分配

3.1 遗传算法简介

遗传算法是一类随机优化搜索方法,该算法直接对结构对象进行操作,不存在求导及函数连续性的限定,具有更好的内在并行性和全局搜索能力;采用概率化的寻优方法,能自动获取优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。该算法一般由:编码、初始群体的生成、杂交、适应度值评估检测、选择、变异和中止7个步骤构成[15]126。

3.2 精度分配优化数学建模

3.2.1 设计变量

转台传动系统的单侧传动链有4个齿轮,根据1.2节的分析,笔者选取齿轮的切向综合误差、齿轮孔与轴颈之间的间隙、安装处轴颈径向跳动误差和轴承径向游隙为系统传动误差设计变量。

由于齿轮1和齿轮4是齿轮轴,其齿轮孔与轴颈之间的间隙及安装处轴颈径向跳动误差的值均为0,转台传动系统的精度分配模型由12个设计变量构成,如表1所示。

表1 精度分配设计变量

3.2.2 约束条件

约束条件直接决定优化结果的准确性。笔者先根据新型转台传动系统中,各齿轮不同精度等级(取5级到8级)选取变量的取值范围,再依据齿轮不同的精度等级查阅机械设计手册,确定每个齿轮的x1、x2、x3及x4的取值范围,如表2所示。

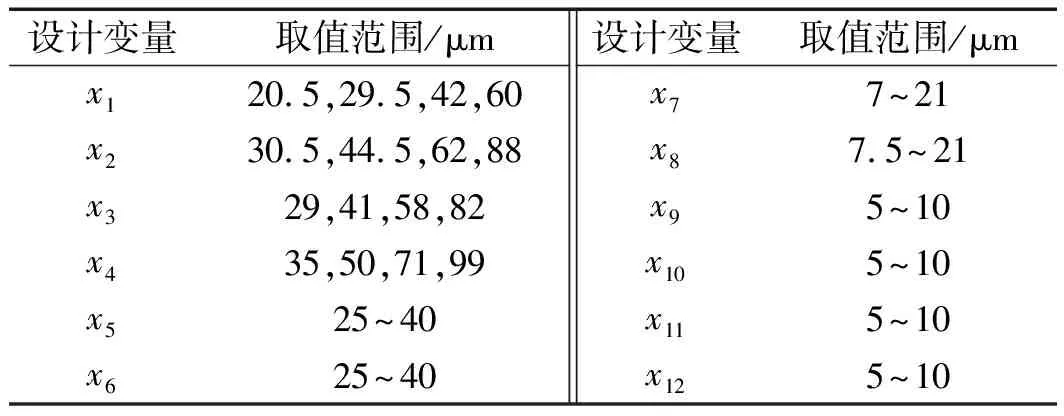
表2 设计变量的取值范围

转台设计的定位精度要求低于8″。由于转台由SINUMERIK-840D全闭环控制系统控制,其定位精度要比开环系统高一个数量级,故满足小于等于80″即可。

基于机床工作时热误差的影响,笔者将误差允许值设定为61″;结合式(13)可得其优化目标应满足误差的约束条件为:

(28)

3.2.3 目标函数确定

目标函数会影响优化模型的性能，由单一目标函数得到的优化解常具有局限性[16]。因此,本文采取多目标优化的方法,设定成本、均衡及鲁棒3个目标函数为优化目标,并用适应度函数对其进行寻优求解,进而得到一个新的适应度函数,最后用遗传算法求解寻优后的新适应度函数,得到合理的精度分配方案。

(1)成本目标函数

降低生产成本是新型转台精度分配的重要目标之一。在多指标评价体系中,由于各评价指标性质不同,通常具有不同的量纲和数量级[17],需对设计变量进行归一化处理,即:

(29)

因此,成本目标函数的公式为:

(30)

(2)均衡目标函数

在精度分配中,应避免出现一个误差值很低,一个误差值很高。另外,由于齿轮误差值具有离散性,应对相应齿轮的轴向跳动误差和径向跳动误差进行均衡化处理[15]125,其均衡目标函数为:

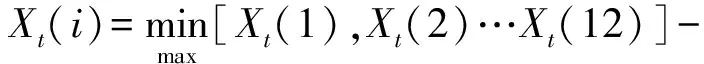
(31)

(3)鲁棒目标函数

为尽量增加转台齿轮传动系统误差的稳定性,可以采取降低设计变量误差值的措施。基于敏感度分析设计鲁棒目标函数为:

(32)

(4)适应度函数转化

适应度函数是按照最小值进行且有约束的,针对线性方程的最优值寻优的函数[14]2913,笔者将以上3个目标函数用适度性函数进行转换,可得:

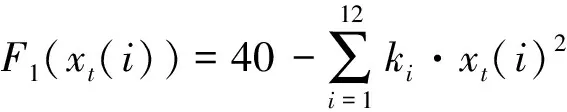
(33)

采用权重法,并结合转台结构,笔者确定成本、均衡及鲁棒目标函数加权系数分别为c1=0.5,c2=0.3,c3=0.2,则简化后新的适应度函数为:

(34)

由于设计要求是,完成精度分配后的转台传动误差的最大求解值要小于转台传动误差设计允许值。但是适应度函数默认求解的是转台传动误差的最小值,需要对适应度函数添加负号,经转换求得精度分配后的传动误差的最大值。用遗传算法所求的函数为:

(35)

满足的约束为:

(36)

3.3 精度分配计算

根据上述理论,笔者使用MATLAB编写多目标优化后的遗传算法程序[18],并取交叉概率0.7,变异概率0.3,进化次数500,种群规模500;运行后得到转台的齿轮优化数据。

前5级精度齿轮参数如表3所示:

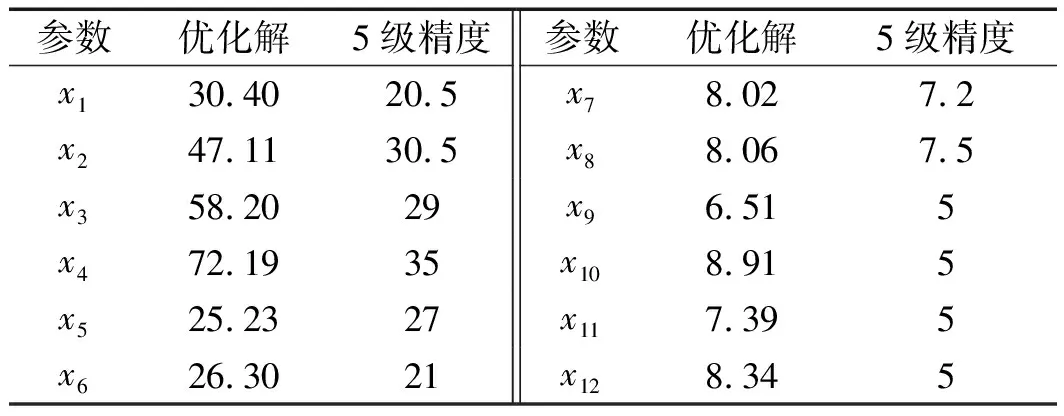
表3 高精度分配方案

从优化结果可以看出:齿轮1、2、4和6的切向综合误差的选取可以适当增大,孔与轴之间的间隙变化不大,安装处轴颈径向跳动误差可以适当提高,轴承径向游隙无明显变化。

根据齿轮的切向综合误差的变化值,笔者对转台传动系统的齿轮进行重新选取。优化后的齿轮精度等级变化如表4所示。

表4 优化前后齿轮精度等级对比

式(27)中,代入精度优化分配前5级精度齿轮参数,经计算可得:传动误差概率统计集中值为18.4″。

同理,代入优化后的设计参数,可得精度优化后的传动误差最大值为54.7″<61″,概率统计集中值为27.61″,小于转台齿轮传动系统设计的允许设计传动误差范围,满足设计要求,可见其精度分配合理。

从优化后的齿轮精度等级表格中可以看出,在满足设计误差要求的前提下,各齿轮的精度等级均有所下降,达到了优化设计目标,降低了制造成本。

4 传动误差模型试验验证

为了验证该传动误差计算模型及齿轮精度分配方案的正确性,笔者以6级精度斜齿轮组的减速机作为载体,搭建实验平台(新型转台已投产,实物不方便拆卸),予以间接验证。

4.1 实验原理

笔者以齿轮减速机作为载体,在变频器和三相电机构成的动力组合的驱动下,实现针对减速机输入转速的无极变速,模拟加工过程中转台的转速变化,实现对现实加工环境的模拟;通过分别连接在斜齿轮输入轴、中间轴和输出轴上的3个角速度编码器,实时监测各轴的实时转速和运动状态;再通过接线端子,将数据实时传送到PCL—833多功能采集卡上,由采集卡采集后传输到工控主机采集数据;然后将数据经过角度转化处理,得到同一时间点各轴的转速值。

最后,笔者再通过MATLAB编程制图,将各点的数据输入其中,形成对应的误差曲线,并与分析结果进行对比,验证理论计算体系的正确性。

实验平台搭建原理如图3所示。

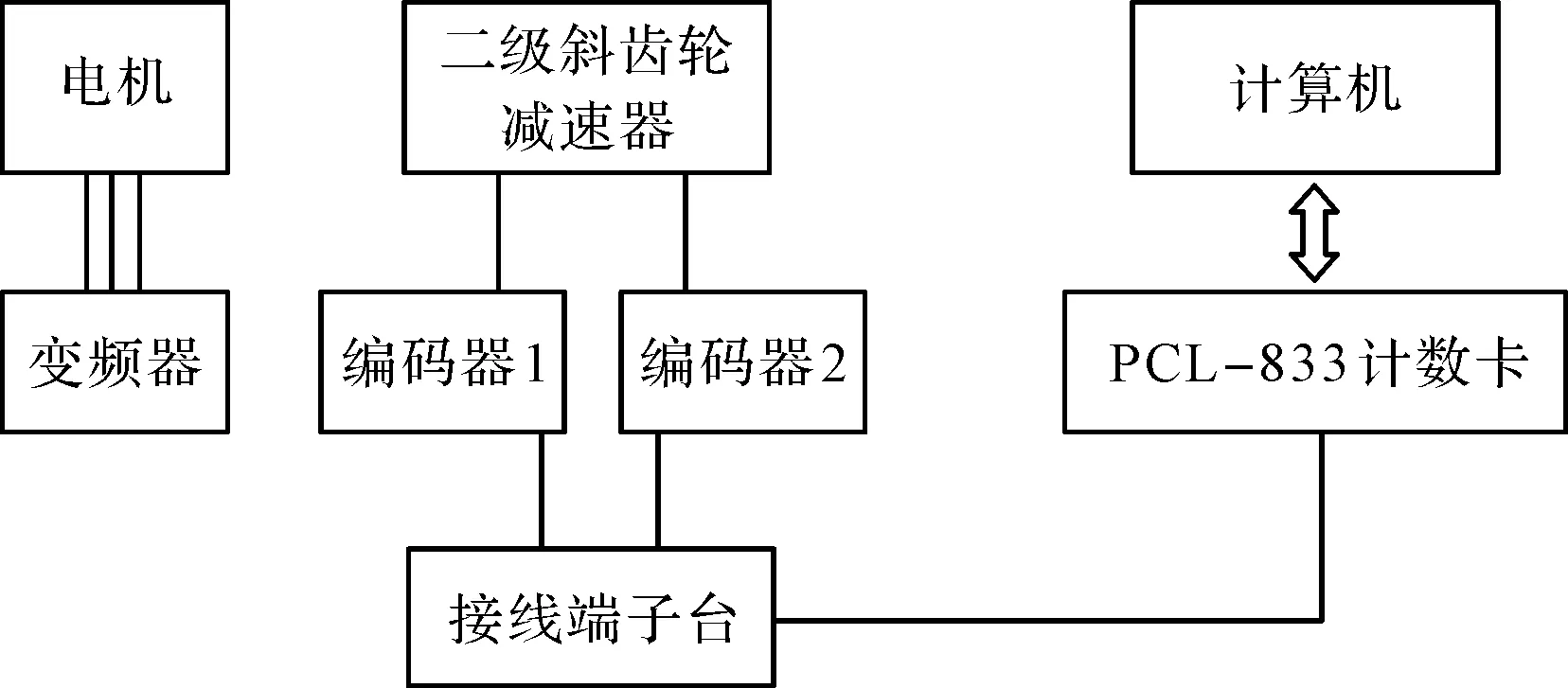
图3 试验平台搭建原理图

图3中,实验平台中检测出的斜齿轮传动系统的传动误差、输入端齿轮副的传动误差和输出端齿轮副的传动误差均能在显示器上,通过PCL833采集卡专用软件界面显示出来。

按实验原理搭建的实验平台如图4所示。

图4 实验平台搭建示意图1—工控主机;2—二级斜齿轮减速器;3—角速度编码器;4—梅花联轴器;5—步进电机;6—变频器;7—PCL833采集卡

4.2 实验数据分析

启动伺服电机后,笔者设置电机转速为10 r/min,运行一段时间待被测齿轮转动平稳后,再开始采集数据,采集数据过程中通过变频器不断变换电机转速(n=10 r/min～960 r/min),得到并记录输入与输出轴的数据,如图5所示。

图5 齿轮传动系统误差采集数据

按PCL833使用说明所述,角度转换公式为:

(37)

式中:Δθ—传动系统的角度误差,分;λ—误差采集值。

笔者不断地记录不同转速下的传动系统误差采集值λ,再按上式将传动误差采集值λ转换成角度误差Δθ[19];最后,用MATLAB编程作图,即得到二级减速器的传动误差曲线,如图6所示。

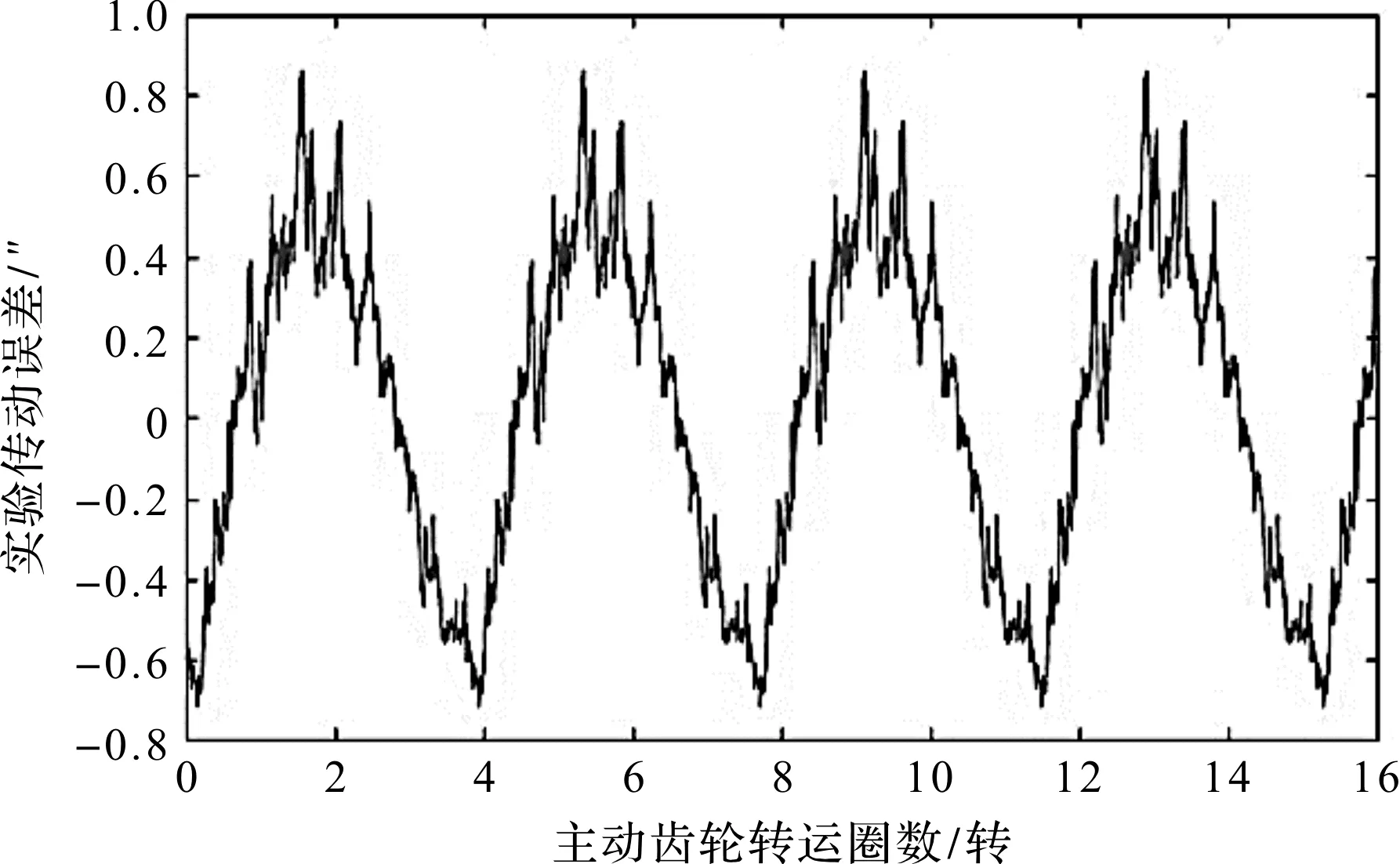
图6 实验测得的系统传动误差曲线

4.3 实验结论

图6中,齿轮传动系统传动误差的绝对值最大为|Δθmax|=0.83′=49.8″,且传动系统传动误差的最集中值为|Δθ集中|=0.42′=25.2″。

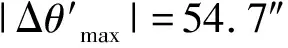
5 结束语

针对齿轮传动系统误差建模分析和精度分配的问题,首先,笔者在概率统计法的基础上建立了齿轮传动系统传动误差的数学计算模型;其次,在传统遗传算法的基础上,对目标函数进行了多目标(成本、均衡及鲁棒性)优化;同时,结合传动系统的实际结构参数,得到了更具有工程意义的适度性函数,建立起了一套精度分配方案;最后,将精度优化分配方案融入到传动系统传动误差计算数学模型中,得到了一套更具鲁棒性和经济性的齿轮传动系统优化设计方案,并用实验验证了其正确性。

研究结果表明:

(1)新传动系统优化设计方案,使传动误差的计算不仅能得到传统极值法所能得到的极值,还能得到其分布规律和均值;同时提高了传动系统优化设计的鲁棒性、经济性及工程实用性;

(2)在满足设计要求的前提下,转台传动系统使齿轮1、2及6精度等级由5级降到6级,齿轮4则由5级降到7级,降低了对单个齿轮的精度要求;同时又免去了对精度分配的人工复核和调整,使齿轮传动系统的设计周期总体上缩短7%,最终使单个转台的成本下降180元,提高了新型转台的经济性。

在后期的研究中,笔者准备从增加精度分配目标数的角度出发,增加目标函数的种类,以期对精度分配方案进行进一步的优化。