直臂式高空作业车稳定性分析及优化研究*

王吉忠,孙亚楠,张西龙,尘 帅

(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)

0 引 言

高空作业车现已广泛应用于建筑、园林、消防、造船、机场等相关高空操作领域[1]。高空作业车可以分为垂直升降式、折叠式、直臂式、混合式等4种主要类型[2]。其中,关于高空作业车辆最基本的安全性能指标,便是稳定性[3]。在实际的工程中,高空作业车在作业过程中因失去稳定性而发生事故的情况比比皆是,不仅对作业车本身造成损坏[4],也对工作人员的生命造成巨大威胁。因此,分析作业车的稳定性很有必要。

很多学者对高空作业车的稳定性进行了分析,并取得了非常有价值的研究成果。例如,王君文[5]利用公式计算出了极限位置的路缘石动态稳定性安全系数。夏林焱[6]通过仿真得到了臂架结构的动态特性曲线,并且分析了臂架的稳定性。宋兴龙[7]利用ANSYS分析了GTB高空作业车典型工况下伸缩臂结构的静强度分析、机构的动力学,并对伸缩臂结构进行了优化改进。王津[8]对一款25 m的高空作业车伸缩臂进行了研究,分析了6种典型工况下臂架的应力变形分布、危险部位及稳定性,并对作业臂进行了拓扑优化,使臂架质量减轻了7.8%。

本研究来源于某公司开发的一种直臂式高空作业车,首先通过仿真核验作业车的稳定性，发现其不能够达到预期效果,然后提出相应的优化方案。

笔者选用ADAMS和SolidWorks软件,建立整车的动力学模型[9-11],根据国家标准进行校核,并提高其稳定性;利用有限元分析方法[12]对伸缩臂进行轻量化设计,提高产品的质量和性能,为之后对高空作业车稳定性的研究提供参考。

1 高空作业车结构以及仿真过程

1.1 作业车主要结构

直臂式高空作业车主要由以下几种部件组成:底盘、主臂变幅液压缸、调平油缸、转台、主臂油缸、基本臂、二号臂、三号臂、折臂、工作平台等。

直臂式高空作业车主要结构如图1所示。

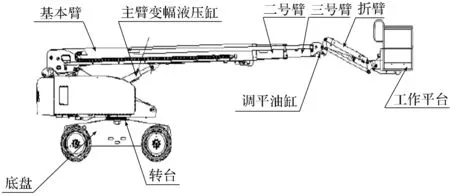
图1 直臂式高空作业车主要结构

1.2 仿真过程

根据该公司的设计图,笔者在SolidWorks中建立三维模型,并对模型中的小零件进行合并、删除等操作,对模型进行适当简化,可以减少计算量,但是在后续仿真过程中需要适当增加质量来保证仿真过程的准确性;

笔者以parasolid格式生成xt文件格式,导入到ADAMS中去;然后在ADAMS中,对各个具有相对运动的连接点设置运动副。其中,基本臂和二号臂、二号臂和三号臂之间是平移副,其他全部为转动副,它们能够限制两个构件之间的相对运动;之后用虚拟模型样机检验后,系统没有多余的约束,就得到了调试好的模型[13]。

下面介绍直臂式高空作业车几种典型的工作状态:

(1)最大高度作业工况。该工况下,伸缩臂全部伸展开,短臂与伸缩臂在一条直线上,且伸缩臂的仰角到达70°;

(2)最大水平延展作业工况。该工况下,伸缩臂全部伸展开,短臂与伸缩臂也在一条直线,且伸缩臂的仰角到达0°;

(3)最大地下延展高度作业工况。该工况下伸缩臂组全部伸展开,短臂与伸缩臂成45°,并且伸缩臂仰角为-10°。

3种工况下作业车的运动范围如图2所示。

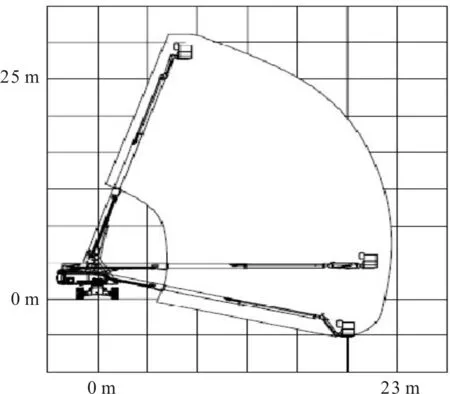
图2 作业车3种工况下的运动范围

根据GB/T9465—2008规定[14],关于高空作业车的稳定性试验分为以下3种:

(1)水平面上稳定。作业车在水平地面上,平台承载1.5倍额定载荷,伸缩机构伸展到整车处于稳定性最差的状态,作业车能够保持稳定;

(2)斜面上稳定。作业车处于坡度为5°的斜面上,平台承载1.25倍额定载荷,作业车能够保持稳定;

(3)作业稳定性试验。平台承载额定载荷,在360°范围旋转,测量轮胎在受力最不利的情况下的支撑反力,要求任一个轮胎都不离地。

在稳定性分析中,为了结果准确,笔者在仿真过程中考虑了风载荷、惯性载荷等,作业车额定载荷为227 kg。

2 水平面上稳定性分析

当直臂式高空作业车在水平面工作时,工作平台不断到达指定的工作位置,这时整机的质心位置不断发生变化。当质心的位置落于水平面的投影在安全区之外时,作业车就有发生倾覆的危险。笔者选用重力法作为研究方法,即稳定区域为两轴之间距离的80%,作业车在各工况下,整机质心轨迹在水平面上的投影不超过这个区域,即为稳定状态。

该作业车经过测量,前后轴中线之间距离为2 730 mm,两前轮中轴线之间距离为2 557 mm。笔者选取4个轮胎围成区域的中心点位置为坐标原点,建立坐标系,沿着原点向伸缩臂伸长方向设为x轴正方向,垂直x轴向里为y轴正方向,垂直作业车向上为z轴正方向。

四轮围成区域的80%为稳定区域,如图3所示。

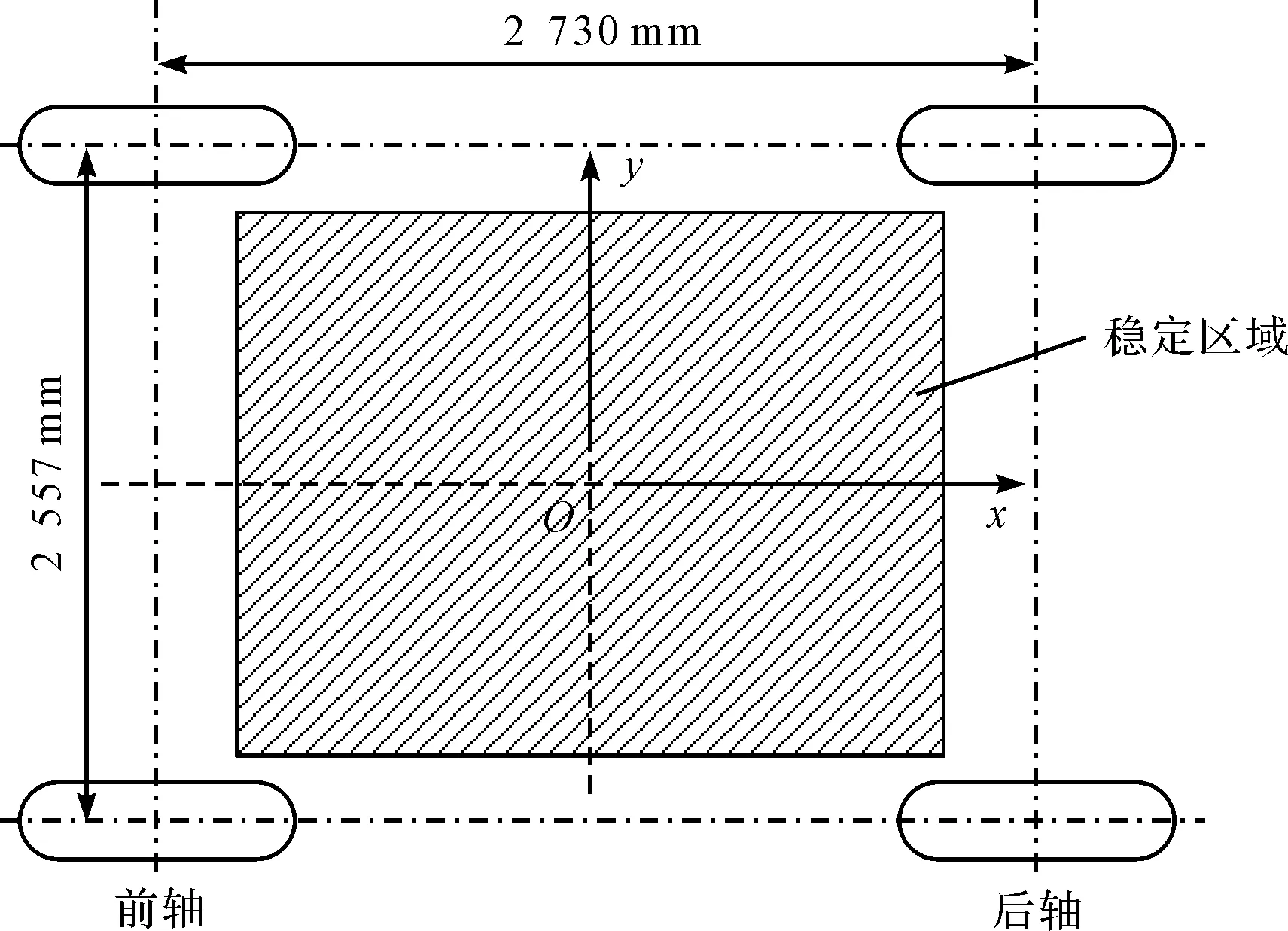
图3 作业车的工作稳定区域

为了保持稳定性,整机质心横向偏距的最大值xmax与纵向偏距的最大值ymax必须小于稳定区域的界限值,即:xmax≤1 092 mm,ymax≤1 022.8 mm。在ADAMS仿真成功后,可以直接得到各个零件的质心坐标。因为整机的质心坐标无法直接从ADAMS中得到,所以这里要运用系统质心求解公式。

质点系质心C的坐标可以表示为:

(1)

式中:M—整机总质量;mi—单个零件的质量;xi—每个零件在直角坐标系中的坐标。

已知质心求解公式,笔者编写质心求解程序,运用该程序可以记录直臂式高空作业车在伸缩过程中,整机质心坐标值的变化规律。具体的编程过程此处不再多加赘述。

2.1 二维空间下的极限工况分析

笔者设定作业车的伸缩臂只在xz平面内运动,伸缩臂不发生旋转,将运动时间设为4个点,其中,0表示最原始作业车未工作收缩状态,1表示伸缩臂伸长到最长状态,2表示到达最大高度工作状况,3表示最大水平延展作业工况,4表示到达最大地下延展高度作业工况;将整车从作业平台到底盘轮胎分为8个部件,首先得到8个部件的质心坐标x、y、z随时间变化的曲线图,可以得到结果为y不随时间变化而变化,所以整机y坐标也是常数,即z轴坐标向平面投影时,只与x有关,将坐标向x轴投影即可;通过利用整机质心求解程序,得到整机y坐标恒为1.198 5 mm,小于整机质心纵向偏距的最大值1 022.8 mm。

x与z的关系如图4所示。

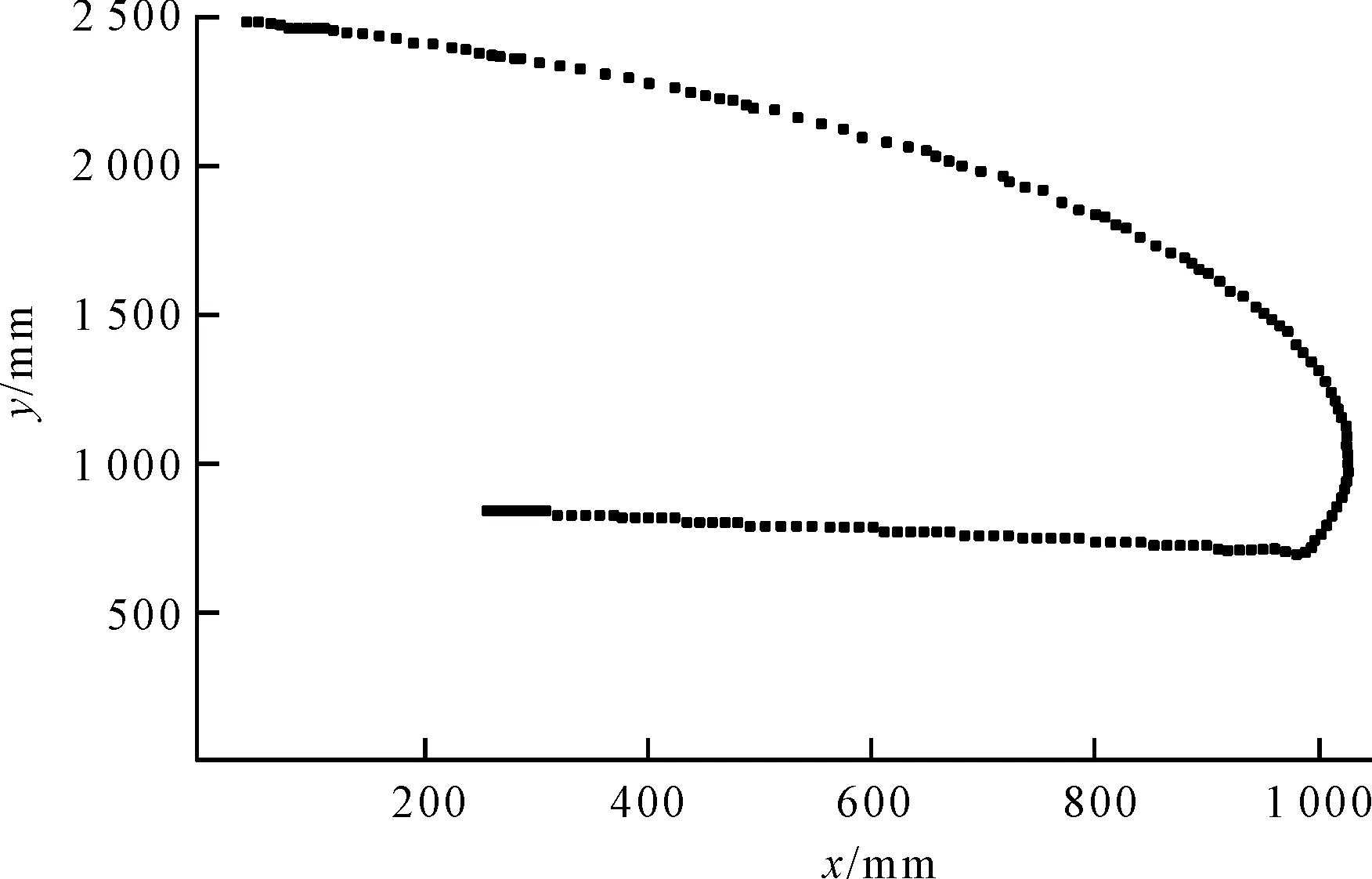
图4 二维空间下的整机质心变化曲线

经过仿真得到最大的x值为1 023.57 mm,小于规定的整机质心横向偏距的最大值1 092 mm,所以可以得到结论,此种直臂式高空作业车在该作业顺序下是稳定的。

2.2 三维空间下的极限工况分析

设定作业车的伸缩臂在xyz三维空间内运动,伸缩臂向y轴正方向旋转90°。同理,笔者将时间设为4个点,其中,0表示初始位置作业车未工作自然收缩状态,1表示作业车伸缩臂边伸长至最长状态边向y轴正方向旋转90°,2表示伸缩臂以最长伸长量在yoz平面达到最大高度工作状态,3表示伸缩臂以最长伸长量在yoz平面到达最大水平延展作业工况,4表示伸缩臂以最长伸长量在yoz平面到达最大地下延展工作状况;运用ADAMS软件,同样得到8个部件的质心坐标x、y、z随时间变化的曲线图,可以得到结果,即在时间1之后,各个部件的质心坐标在x轴分量为常量,而整机质心轨迹在水平面上的投影与z轴无关,只考虑x、y两个方向的坐标即可。

通过利用整机质心求解程序,得到了x、y、z的关系如图5所示。

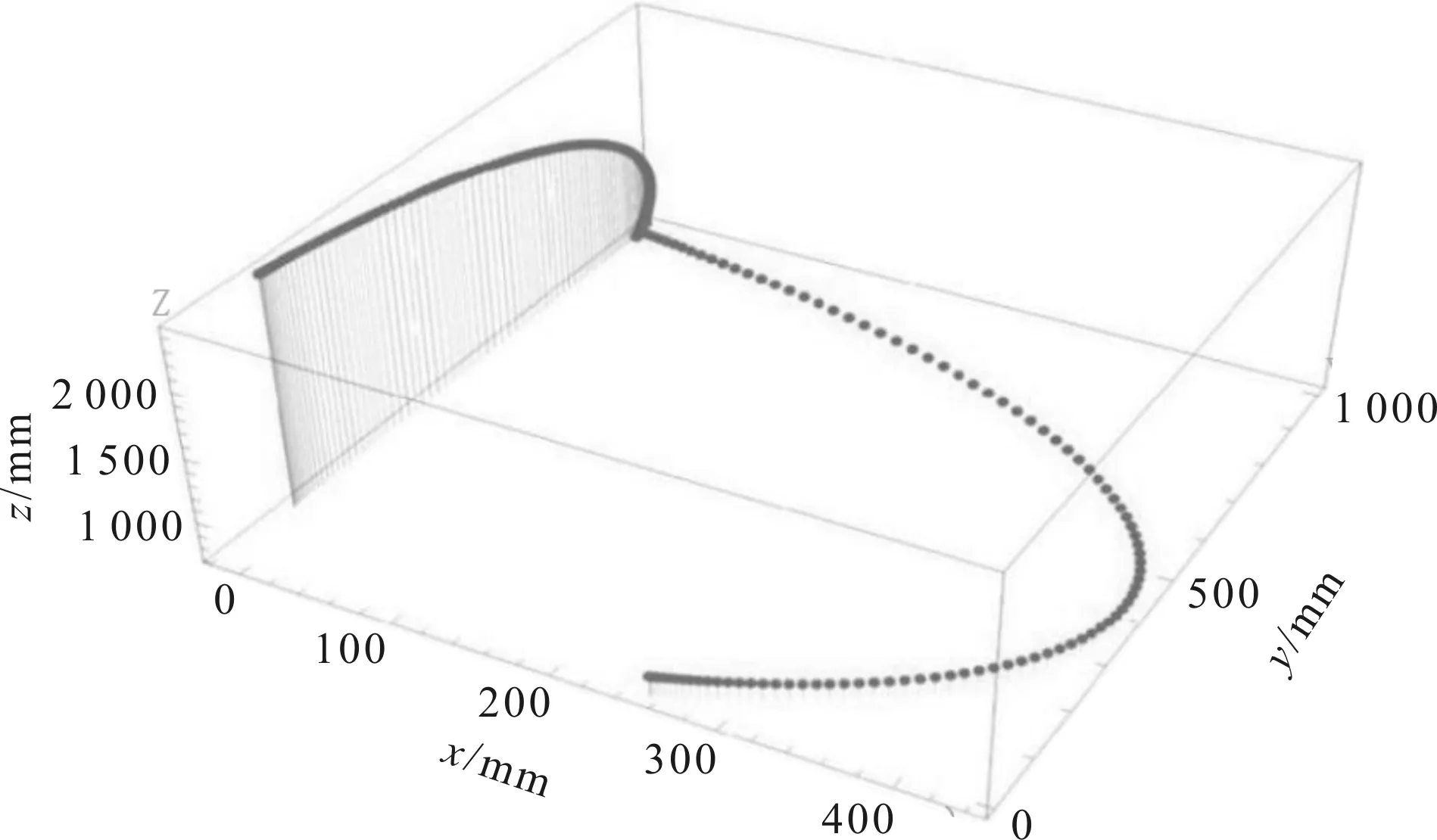
图5 三维空间下的整机质心变化曲线

通过仿真得出数据,x方向最大的坐标为441.836 mm,小于规定的整机质心横向偏距的最大值1 092 mm,y方向最大的坐标为1 002.91 mm,小于规定的整机纵向偏距的最大值1 022.8 mm,所以可以得出结论,此种直臂式高空作业车在此作业顺序下为稳定的。

同理可得,当旋转角度为180°、270°和360°时,与上述两种情况相同,文中不再赘述。

3 斜面上稳定性分析

高空作业车处于坡度为5°的斜面上,平台承载1.25倍额定载荷,这时需要考虑伸缩臂工作时产生的惯性力,为了简化计算,笔者附加伸缩臂水平惯性力的效果[15，16]。

水平惯性力PH按照工作平台与铅垂线夹角α所引起的水平方向分力计算,α取最大值,用PQ来表示工作载荷,惯性力PH=PQtanα;

将4个轮胎处理成均与地面接触,作业车做俯仰动作,伸缩臂从最大地下延展工况到最大高度作业工况的全过程,分别测量地面对轮胎的支撑反力,如图6所示。

从图6中可以看到,支撑反力大部分时间为0,此时高空作业车轮胎与地面接触力为0,发生倾覆的可能性较大[17],作业车非常不稳定。

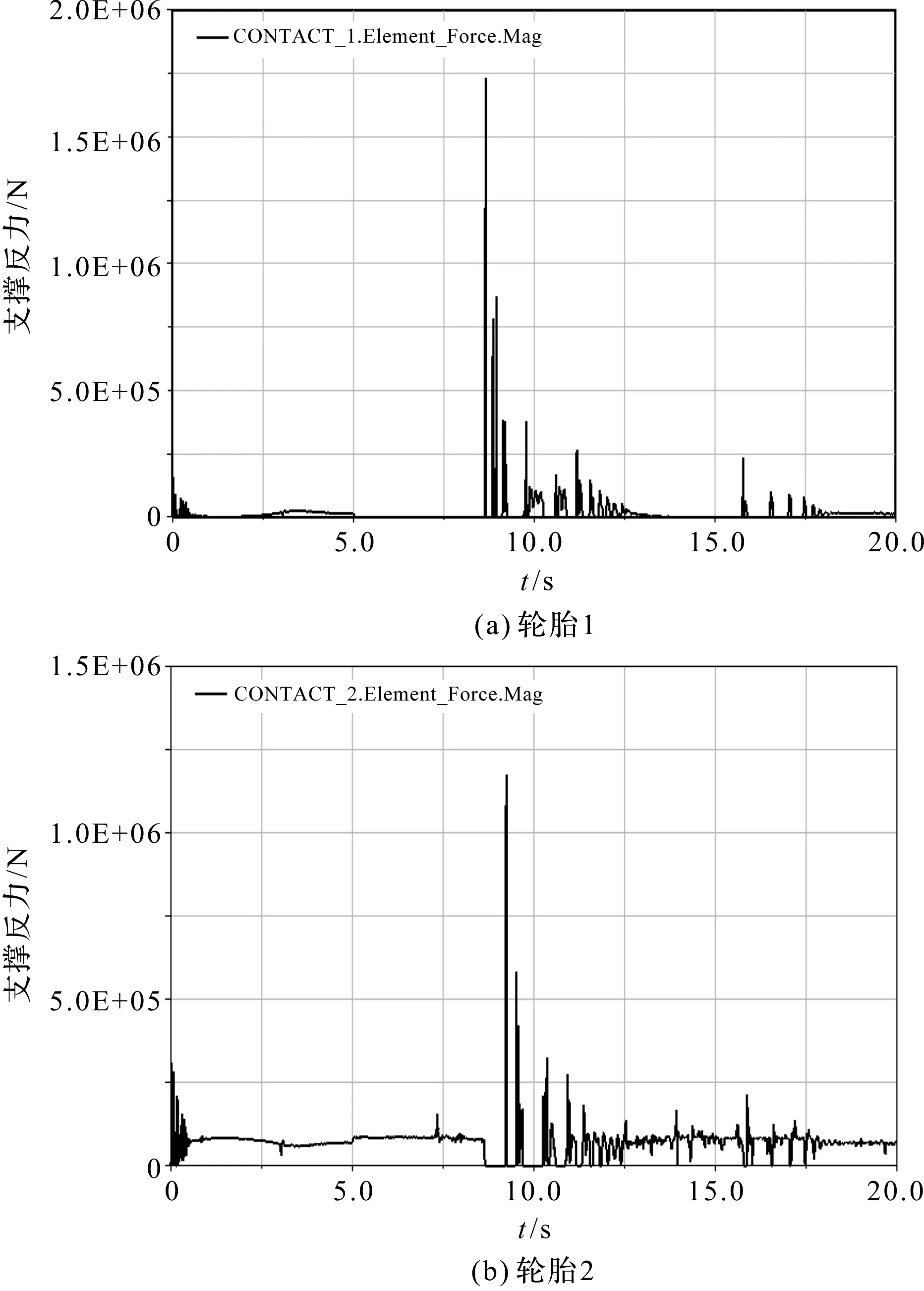
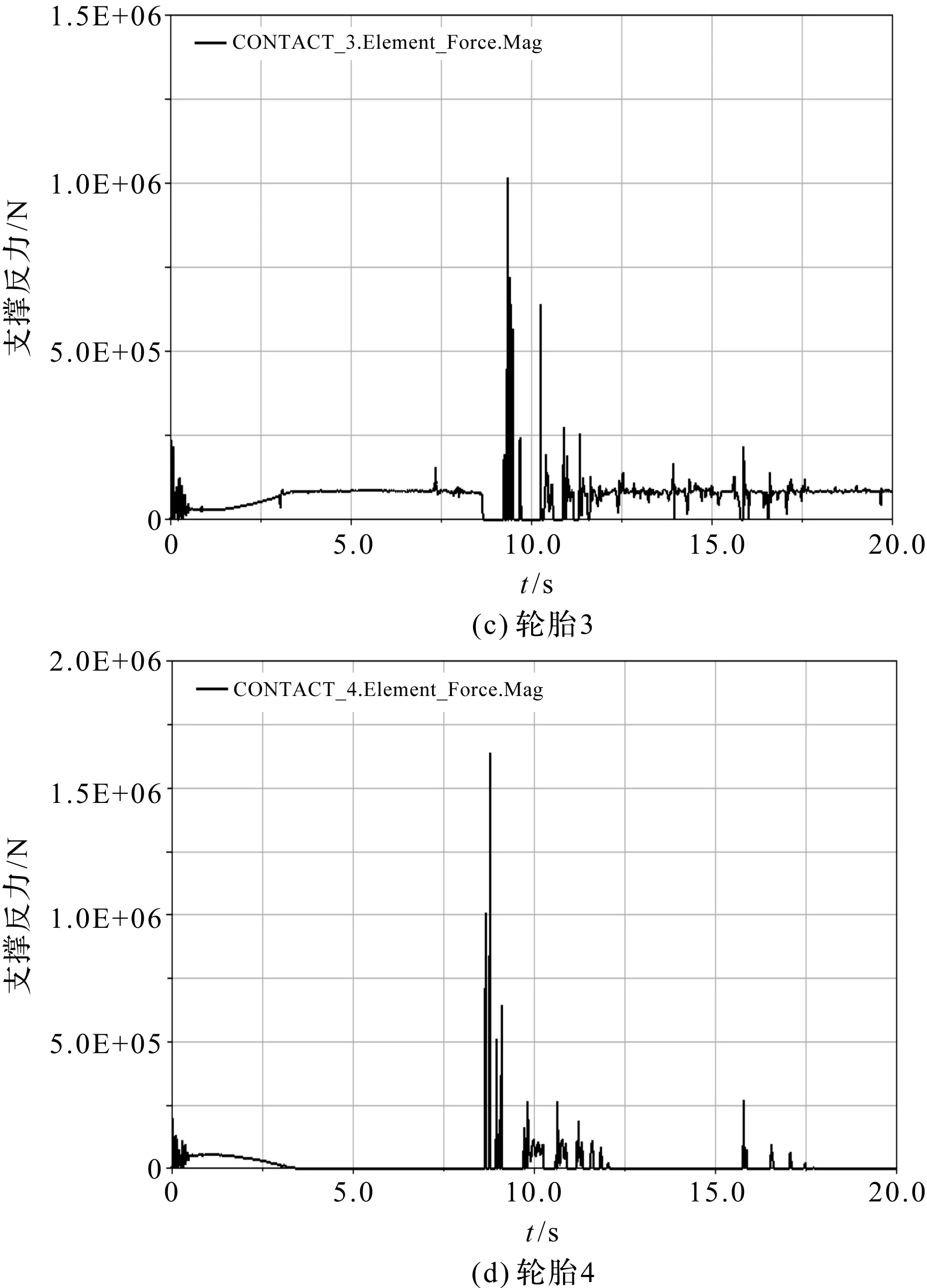
图6 斜面上4个轮胎的支撑反力

4 作业稳定性试验

根据国标规定,平台承载额定载荷,在360°范围旋转,测量轮胎在受力最不利的情况下的支撑反力,要求任一个轮胎都不离地。

仿真结果如图7所示。

图7 作业稳定性试验4个轮胎的支撑反力

该结果与斜面上所得结果相似,支撑反力大部分时间为0,由此可以得出结论,该作业车稳定性存在较大问题,需要优化结构以提高其稳定性。

5 优化及结果分析

5.1 增加配重

为了改善作业车的稳定性,笔者决定适当增加作业车的配重。参考其它同类型的高空作业车、整车总质量,以及考虑到轮胎的承重能力,笔者将配重质量定为8 200 kg。

优化后的模型如图8所示。

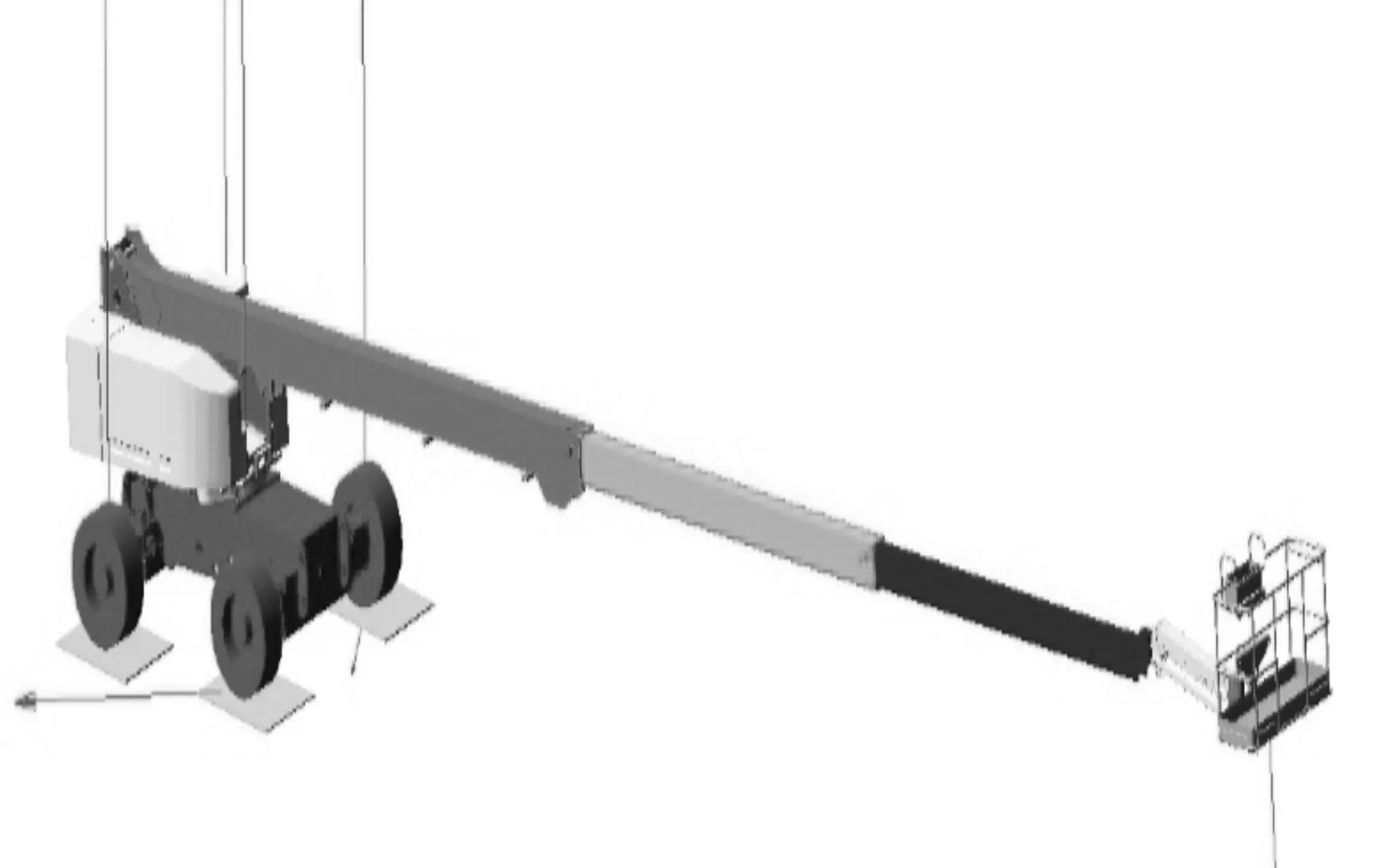
图8 带有配重的作业车模型

笔者对优化后的模型重新进行仿真,发现斜面上4个轮胎的支反力仍有少数为0的情况,考虑到实际情况,将配重质量增加1 000 kg,得到前后对比结果如图9所示。

图9 增加配重质量前后对比图

图9结果证明,适当增加配重质量对改善作业车稳定性有一定的作用,但仍存在局部为0的点,需要进一步进行优化。

5.2 伸缩臂结构拓扑优化

考虑到伸缩臂结构对高空作业车稳定性影响较大,笔者对伸缩臂结构进行拓扑优化,应用Abaqus软件,基于变密度法对其臂架结构的材料分布进行优化[18]。

笔者首先对模型进一步简化,去掉一些孔、圆角等对整体优化影响不大的小特征,对三节臂进行网格划分,并创建拓扑优化模型,以应变能和体积作为设计响应,最小应变能作为目标函数,不大于70%体积作为约束条件,计算模型经过49次迭代,体积约束逐渐逼近初始体积的70%之下,并达到了收敛,证明优化切实有效。

最终优化结果如图10所示。

图10 优化后三节伸缩臂应力和变形情况

图10中,优化后基本臂最大应力约为65 MPa,变形约为11 mm;二号臂应力为约72 MPa,变形量为14 mm;三号臂应力约为66 MPa,应变约为12 mm。由此可见,以上结果满足结构强度要求[19],且降低了约30%的自重。

笔者将优化后的模型重新导入ADAMS中,得到4个轮胎的支撑反力对比图,如图11所示。

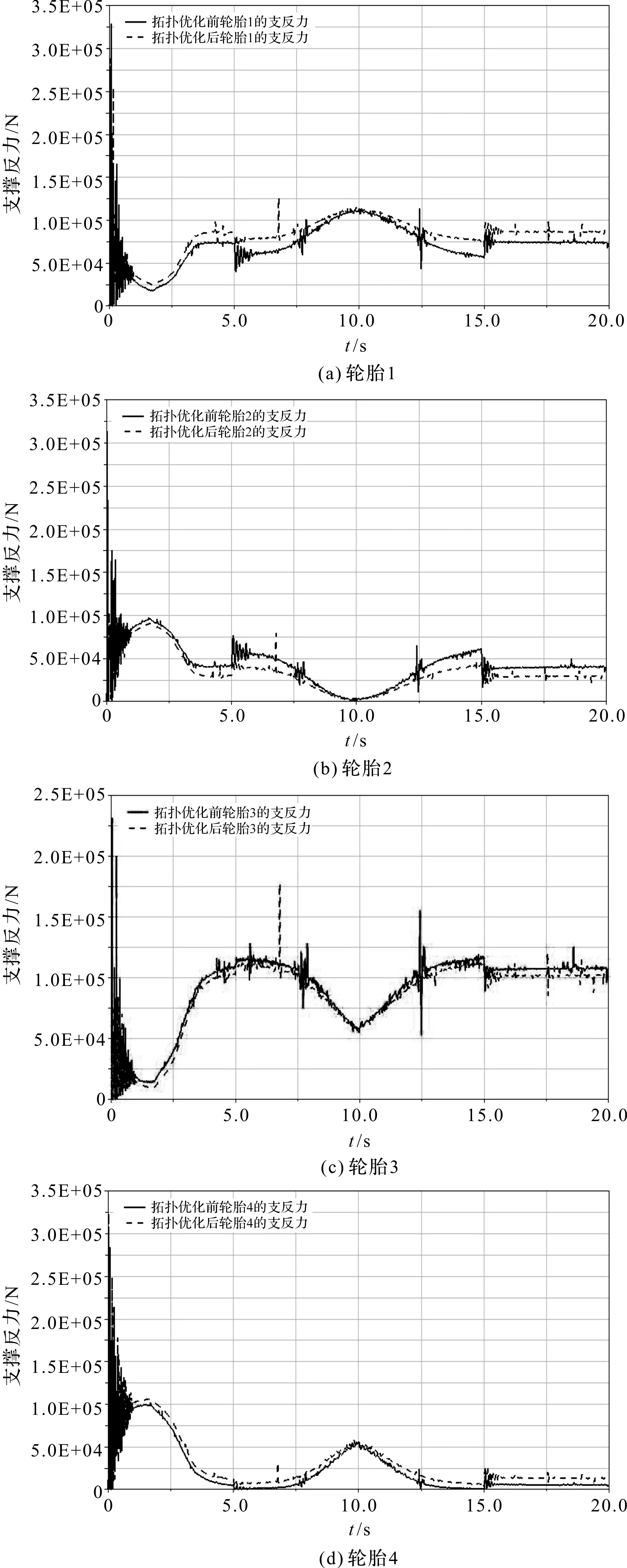
图11 拓扑优化前后对比图

根据仿真结果,4个轮胎中最小的支撑反力是1 300 N,由于图中比例尺的选取较大,因此1 300 N的力看起来数值为0,但实际上在极限工况下,仍然有较大的安全容量。

伸缩臂轻量化使整车质量进一步减少,轮胎与地面接触有所改善,极大地增加了作业车的稳定性,在实际生产中是一种可行的方法[20]。

6 结束语

某公司开发的一种新型直臂式高空作业车存在稳定性问题,本研究运用SolidWorks、ADAMS软件对高空作业车进行了建模和仿真分析,利用有限元分析方法对其进行了优化,提高了高空作业车的稳定性。研究结果表明:

(1)增加9 200 kg配重后,作业车稳定性有了极大的提高,但局部仍存在失稳;

(2)对伸缩臂进行拓扑优化后,体积减少到原来的70%,稳定性也大幅提高。

该方法被证明是切实有效的。在后续研究中,笔者将致力于把作业车的形状和质量变得更小，同时让作业车的承载能力更强、作业幅度更大、智能化升级。