基于振动信号显著性序列的滚动轴承状态诊断方法研究*

刘志翔,朱 明,付 铭,梅 杰,徐 惠,聂德鑫,李永祥

(1.国网山西省电力公司 电力科学研究院,山西 太原 030001;2.华中科技大学 电子信息与通信学院,湖北 武汉 430074;3.南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106;4.国网电力科学研究院 武汉南瑞有限责任公司,湖北 武汉 430074)

0 引 言

滚动轴承大量使用于机械、电力等系统中,其运行状态与设备整体性能息息相关,如果轴承发生故障,则会造成设备运行不稳定,严重时甚至会发生人员伤亡事件[1-3]。

把振动信号用于滚动轴承故障诊断十分有用,如何提高基于振动信号的滚动轴承状态诊断率是当前热门的研究方向[4,5]。其中,机器学习对于识别轴承各运行状态较为有效。但在故障早期,滚动轴承振动信号的特征信息微弱,受到噪声干扰较大[6,7],所以仅将振动信号输入机器学习模型中直接分类,轴承状态诊断效果并不理想。因此,找到一种合适的信号处理方法,与机器学习相结合,提高基于振动信号和机器学习的滚动轴承状态诊断正确率具有重要意义。

近年来,利用信号处理技术提高轴承状态诊断准确率的研究方向主要集中在频域和时频域。文献[8,9]将滚动轴承振动信号的频域统计指标输入机器学习模型,实现了对轴承状态的诊断,但是该方法无法适用于复杂的应用场景[10]。文献[11,12]将轴承振动信号通过短时傅里叶变换得到振动图像,输入至深度学习模型中，对轴承进行了状态诊断;但是将振动信号转为二维图像时,破坏了时域数据间的关联度[13]45-46,而时域信号保存着滚动轴承最全面的信息[14,15]。李文峰等人[16]提出了TALAF和THIKAT两个时域指标,提高了轴承故障预测的准确性;但该方法不能与机器学习相结合。EREN L等人[17]将轴承信号输入卷积-长短时记忆递归神经网络中,对轴承进行了状态诊断;但该方法没有对有噪声情况进行测试。

综上所述,本文从时域信号角度出发,提出一种基于振动信号显著性序列的滚动轴承状态诊断方法。该方法通过将振动信号进行谱残差运算得到显著性序列,并输入到机器学习网络中实现轴承状态诊断。

1 显著性序列

显著性序列是通过对振动信号进行谱残差处理而得到的。谱残差视觉显著性理论由HOU Xiao-di[18]于2007年首次提出,在图像处理领域得到了广泛应用。

SHEKAR B H等人[19]利用谱残差显著图对视频镜头边界进行了检测,该方法对大多数视频给出了较高的准确率、召回率和F1-score。LIU Kun等人[20]将谱残差与相位谱加权结合在一起构造显著图,对有雾天气下道路上的物体进行了检测。LI Shao-dan等人[21]采用谱残差模型,对卫星图像进行了目标检测,发现该方法适合从卫星图像中快速提取农村居住区。闫成章等人[22]利用谱残差对合成孔径雷达图像进行了显著性检测，得到了显著图,用以检测不同状况下的合成孔径雷达图像船舶目标。QIN Yao等人[23]将谱残差用于害虫的边缘检测,该方法能准确地检测出害虫的位置,提高了边缘检测的效果。REN Han-sheng等人[24]于2019年将该方法应用于一维时间序列,从而实现了对时间序列进行异常检测;但是该方法尚未在状态诊断领域得到应用。

1.1 显著性序列算法步骤

从信息论的角度来看,有效编码可将振动信号分为两个部分,分别为信号特征部分和由编码系统抑制的冗余信息,这种冗余对应于环境的统计不变性。通过去除冗余信息,就可以获得信号特征部分,即显著目标[25,26]。

显著性序列算法主要包括3个步骤:(1)获得振动信号的对数幅度谱和平均对数谱;(2)获得信号的谱残差;(3)获得信号的显著性序列。

显著性序列具体流程如图1所示。

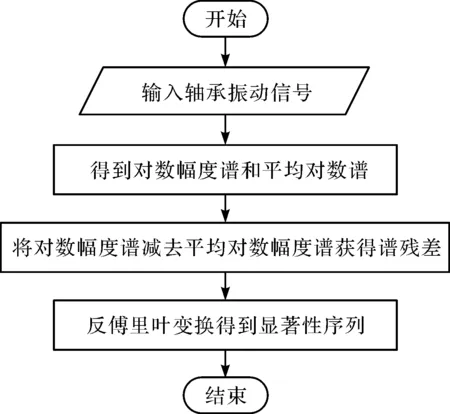
图1 针对滚动轴承的显著性序列流程图

(1)首先，将原始振动信号分为若干个相同长度的子序列,并对子序列进行归一化处理;然后，对该信号进行傅里叶变换,得到其幅度谱F(x),并进行对数运算，得到对数幅度谱L(f);最后，将对数幅度谱与滤波器hq进行卷积运算,得到平均对数谱AL(f)。其中,滤波器为非局部均值滤波器,相对于原显著性序列方法选取的局部均值滤波器对滤波器内时间序列作平均,该滤波器可以更突出时间序列的特点。

平均对数谱AL(f)表达式为:

AL(f)=L(f)*hq

(1)

式中:q—设定的局部均值滤波器的大小。

其中:

(2)谱残差R(f)可通过对数幅度谱L(f)减去平均对数谱AL(f)获得,即:

R(f)=L(f)-AL(f)

(2)

(3)显著性序列可由谱残差经过傅里叶逆变换映射回时间域得到,其计算方法为:

S(x)=‖F-1[exp(R(f)+iP(f))]‖

(3)

式中:F-1—傅里叶逆变换;P(f)—原振动信号序列x的相位谱。

P(f)计算公式如下:

(4)

式中:Im(F(x)),Re(F(x))—振动信号经傅里叶变换后得到的频谱虚部和实部。

1.2 轴承振动信号数据集

本文利用美国凯斯西储大学的轴承故障公开数据库[27]完成滚动轴承状态诊断的验证工作。该数据通过加速度传感器采集得到,其中,传感器采样频率为12 kHz和48 kHz两种。待测轴承共包含正常、球外故障、内圈故障和外圈故障4种状态,故障类型为使用电火花加工引入单点故障。轴承型号共有两种:(1)SKF型号轴承,引入的单点故障直径为0.007 inch,0.014 inch,0.021 inch;(2)NTN型号轴承,引入的单点故障直径为0.021 inch和0.028 inch。

两种型号的轴承分别在0 hp、1 hp、2 hp、3 hp的电机负载工况下运转[28,29],待测轴承及其状态如表1所示。

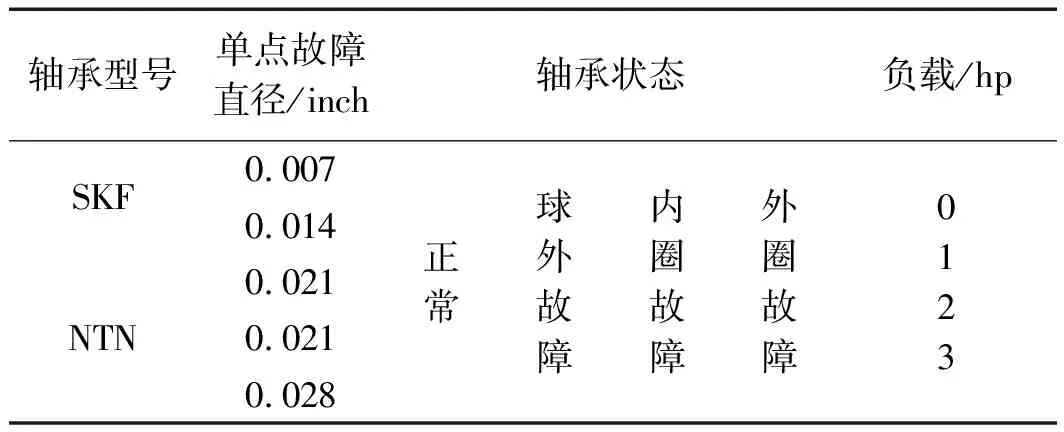
表1 待测轴承及其状态

1.3 显著性序列结果

1.3.1 原始振动信号与显著性序列

在本次实验中,笔者将以正常状态,直径为0.007 inch的球外故障、内圈故障和外圈故障4种数据为例进行论述。

实验装置由电动机驱动,在负荷为0 hp时,电动机上的转轴以恒定速度1 797 r/min转动,其旋转频率为转速除以60,信号采样频率为12 kHz,则轴承旋转一周的采样点数为采样频率除以旋转频率,约400。

由1.2节知,实验装置在0 hp、1 hp、2 hp、3 hp 4种负荷条件下运行,笔者据此将数据集分成4类,每类包含以上几种运行状态的振动信号数据集。笔者选取负载为0 hp数据集下的4类轴承振动信号进行归一化处理,然后画出相应的时域波形图及其对应的显著性序列,如图2所示。

图2 不同状态下轴承原始振动信号及其显著性序列

由图2可以发现,显著性序列较原始振动信号有部分显著突出点。

观察原始信号和显著性序列的频谱图,如图3所示。

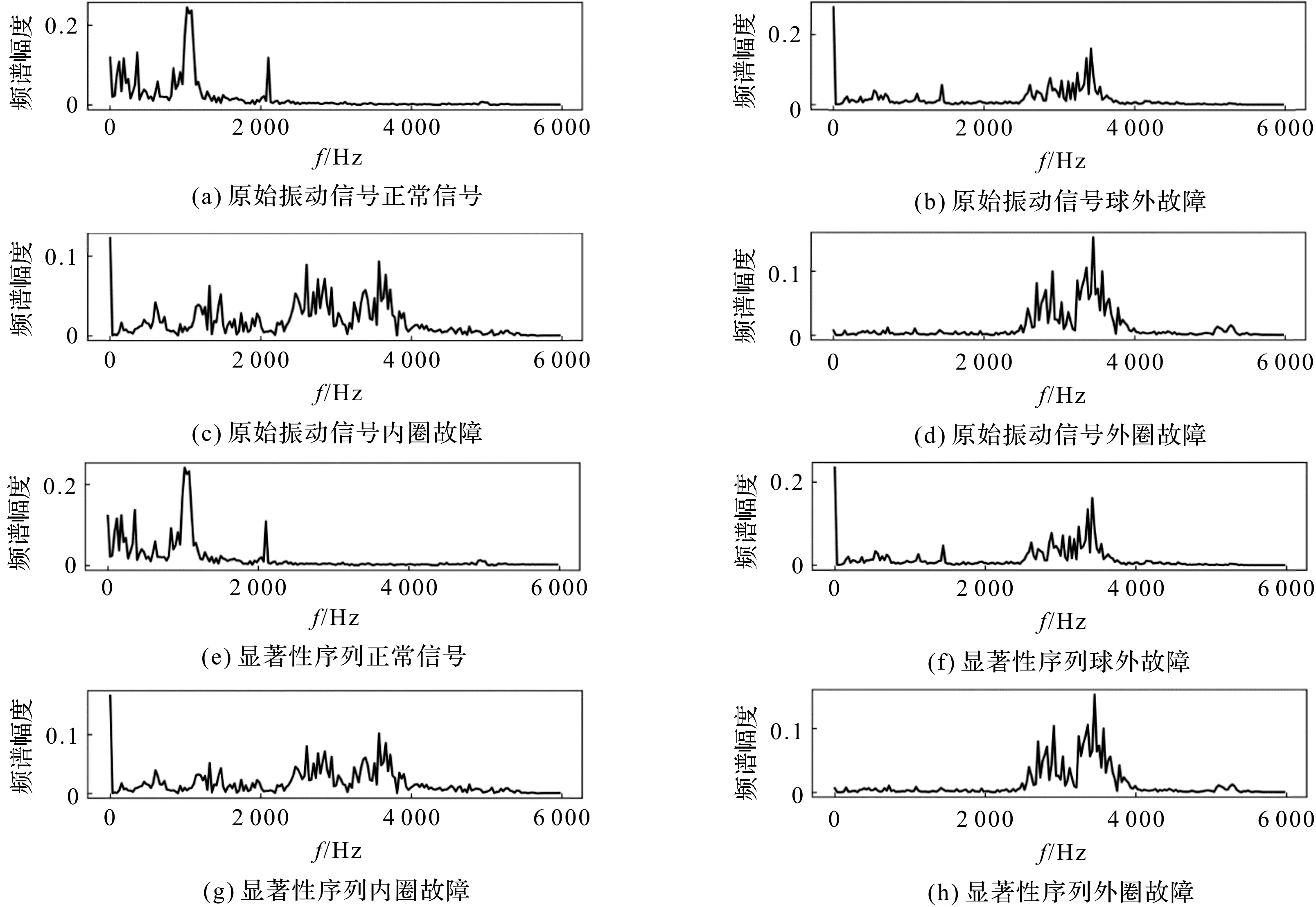
图3 原始振动信号及其显著性序列的频谱图

由图3发现,信号在高频时较原始振动信号的频谱图凸起更为明显,尤其对于正常信号,在频率为5 000 Hz时,显著性序列较原始振动信号的幅度更大。由此可见,显著性序列在一定程度上放大了原始振动信号中具有显著特征的频率。

1.3.2 不同噪声下原始振动信号与显著性序列

图2给出的振动信号的信噪比(signal-noise ratio, SNR)很高,偏向于实验室理论研究验证。而在实际应用中,轴承的工作环境会包含一定量的噪声。

下面笔者将利用对原始振动信号添加不同信噪比的高斯白噪声,模拟现实生产生活中的不同环境噪声对振动信号的影响,从而分析显著性序列对于含噪信号的影响。

对图2的原始振动信号加入信噪比为-6 dB的噪声，获得含有噪声的信号,如图4所示。

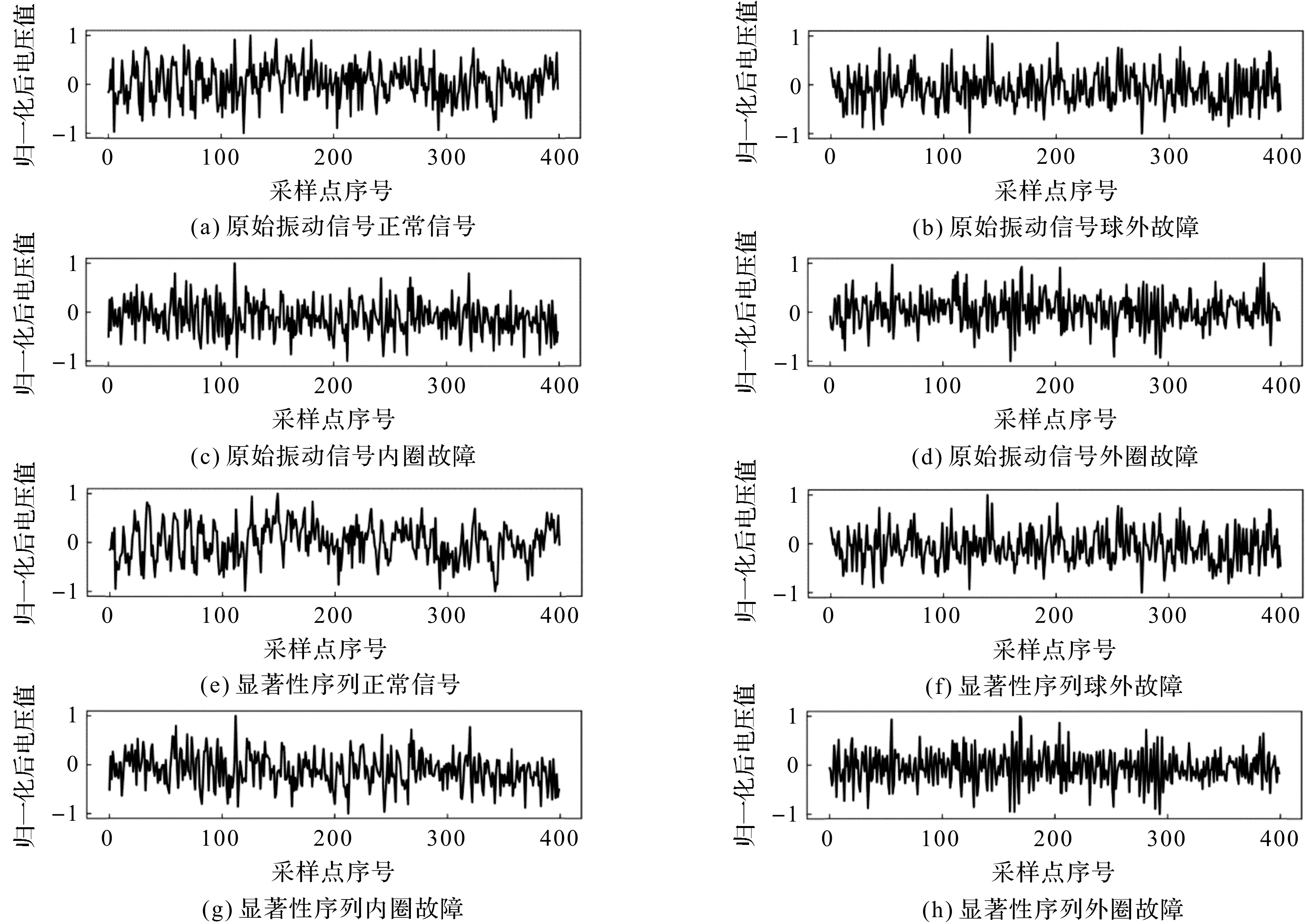
图4 加入信噪比SNR=-6 dB噪声时的原始振动信号及其显著性序列

由图4可知,含有噪声的原振动信号与未加噪声的图2相比,周期性规律已很不明显,即图4(a～d)信号之间的区别几乎无法用肉眼辨别;而图4(e～h)显著性序列较原始振动信号图4(a～d)能显示出一定规律性,图4(e～h)信号之间的变化趋势已被显著增强,特别是图4(e)的低频周期性已然显现。

同时,笔者对比观察无噪信号频谱图(图3)和含噪信号频谱图,如图5所示。

图5 含SNR=-6 dB高斯白噪声原始振动信号及其显著性序列的频谱图

图5中,与未加噪声的图3相比,加入噪声后原振动信号的频谱图较难看出其频率特征,而图5中显著性序列在频率较高时的频谱幅度较原始振动信号有明显减小,即显著性序列对于高频噪声频率有抑制作用。

综合考虑0 hp数据集下无噪声的显著性序列及含噪声的显著性序列较原始振动信号的变化,可以发现,显著性序列对无噪声信号的微小特征频率有放大作用;同时,对于噪声信号的频率有抑制作用,这对于发现和获取振动信号特征具有很大帮助作用。

本节通过时域图和频域图对显著性序列有了一些直观了解。而能否利用显著性序列提高振动信号的分类识别,提升振动状态诊断率，是本文的研究重点。

2 状态诊断模型及参数选择

当前状态诊断模型主要采用机器学习模型,本文将分别利用传统机器学习模型支持向量机和深度学习模型卷积神经网络,验证显著性序列对振动状态诊断率的提升。

2.1 支持向量机参数选择

支持向量机[30,31]是一种典型的二分类问题。决策函数只依赖于支持向量,与训练样本总数无关,分类速度比较快,其参数包括核函数、惩罚系数和核函数系数。一般经验下,核函数首选高斯径向基函数。对于惩罚系数C,C越大,在训练样本中准确率越高,但是容易过拟合;C越小,容易欠拟合。对于核函数系数γ,γ越大,支持向量越少;γ越小,支持向量越多,而支持向量的个数影响训练和预测的速度[32,33]。

在一定程度上,显著性改变了数据分布特点;因此，本文选择能分别使原振动信号和显著性序列均达到最大准确率的参数。对于原振动信号,C确定为10,γ确定为0.06;对于显著性序列,C确定为10,γ确定为0.03。

2.2 卷积神经网络参数选择

卷积神经网络是一种可对输入信号进行特征提取和分类的前馈神经网络,其结构层次包括卷积层、激活层、池化层和全连接层[34-36]。

许爱华等人[13]47指出,通过增加CNN网络层数的方法提高模型训练和测试的准确率,仅针对二维(如图像)、三维数据才有效,而针对本文中所采取的一维数据,大幅度增加网络层数对于提升训练和测试的准确度没有明显效果。本节通过选择合适的网络参数及网络深度,可提高网络的性能。

影响卷积神经网络分类准确率的因素主要有优化器、学习率、批处理样本数量、网络结构及卷积层超参数的选择等[37,38]。其中,优化器可以尽可能地在不过拟合的情况下降低损失值,学习率可以影响优化器的收敛速度。对于批处理样本数量来说,数量过大,模型训练时间过长、数量过小,模型会难以收敛。对于卷积核尺寸来说,卷积核过大,模型的参数会变多,模型性能变低,卷积核过小,则对稀疏数据的特征提取不友好。

为有效减少模型参数以及保证模型特征提取能力,本文选择Adam作为CNN网络的优化器,学习率为0.001,批处理样本数量定为64,卷积层定为3层,其中,第一、二、三层卷积层的卷积核大小均设为1×3。

3 实验验证

按照第2节所设定支持向量机和卷积神经网络的参数,笔者搭建滚动轴承故障诊断模型,并分别在无噪及含噪条件下进行实验,得到相应的诊断正确率,从而对显著性序列是否能提高时域下振动信号的诊断准确率进行验证。

具体实验流程如图6所示。

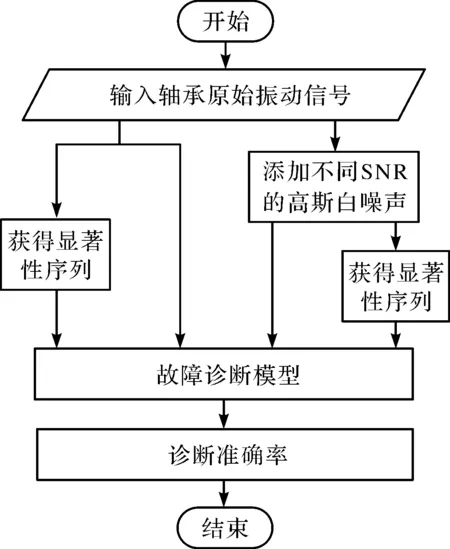
图6 实验流程图

3.1 支持向量机实验结果

按照2.1节所设定参数,笔者分别在无噪及含噪条件下进行实验,得到对应的诊断正确率。

首先,针对无噪信号,笔者在负载为0 hp、1 hp、2 hp、3 hp的数据集进行测试,其结果如表2所示。

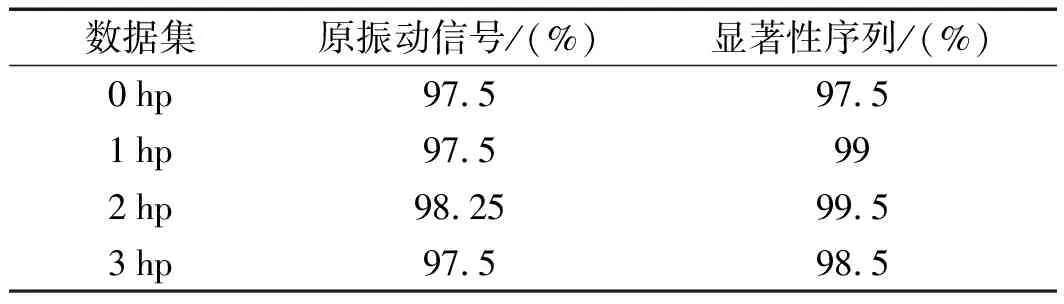
表2 不同负载下显著性序列与原始振动信号的诊断正确率

可以发现,对0 hp数据集,两者可达到相同诊断率;但对1 hp、2 hp、3 hp数据集,显著性序列的诊断准确率较原始振动信号有一定提高,特别是2 hp的诊断准确率可提高到99.5%。

针对含噪信号,笔者以0 hp数据集为例介绍实验结果。为便于直接对比,将显著性序列与原始振动信号分别加入相同信噪比的高斯白噪声后,输入到“相同”SVM模型,得到的正确率结果如图7所示。

图7 不同信噪比的高斯白噪声下原始振动信号和显著性序列的分类正确率

由图7可知,较原始振动信号,显著性序列对于含噪信号的分类准确率有一定提高;且相对于原显著性序列选取的局部均值滤波器,非局部均值滤波器很好地解决了对于加入SNR=-4 dB的噪声之后准确率下降的问题。

由此可见,显著性序列可以更好地提取研究对象特征,具有一定的抗噪声能力,可适用于包含噪声的振动信号。

3.2 卷积神经网络结果

与3.1节相同过程,笔者按照2.2节所设定参数,分别在无噪及含噪条件下进行实验。实验所使用的CNN通过Pytorch实现,操作环境为一台使用i5-3210中央处理器的计算机,未采用GPU加速。

针对无噪信号,本文CNN在负载为0 hp、1 hp、2 hp、3 hp下的数据集测试结果,如表3所示。

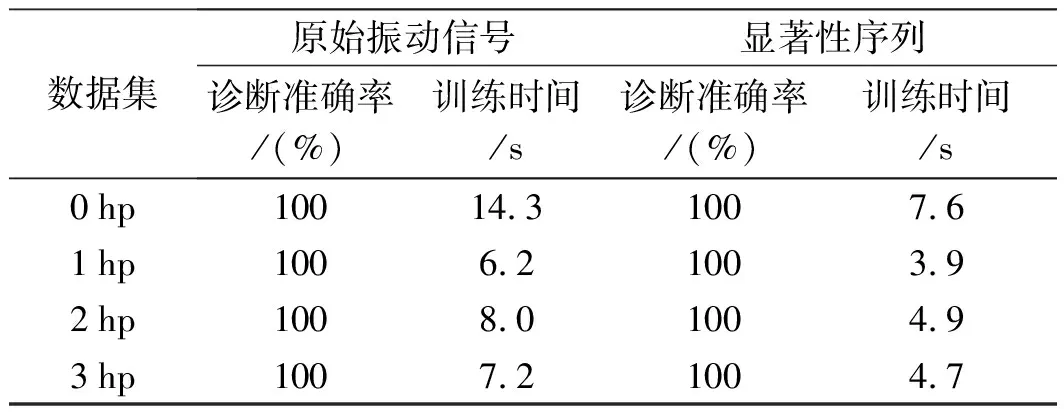
表3 不同负载下显著性序列和原始振动信号诊断正确率

由表3可知,在4个数据集下,显著性序列和原始振动信号的诊断正确率均达到100%;但在达到相同诊断准确率时,显著性序列较原振动信号用时更短,效率更高。该结果说明,显著性序列提高了4类运行状态的区别度。

针对含噪信号,笔者仍以0 hp数据集为例介绍实验结果,将显著性序列与原始振动信号分别加入相同信噪比的高斯白噪声后,输入到“相同”CNN模型,得到了分类正确率结果,如图8所示。

图8 不同信噪比的高斯白噪声下原始振动信号和显著性序列的分类正确率

由图8可知,显著性序列比原始信号识别率都有一定提高,特别在SNR较小,例如为-6 dB时,较原始振动信号直接输入卷积神经网络进行分类,显著性序列正确率从71.5%提高到了82.25%。因此,显著性序列具有更好的抗噪声能力,更适用于包含噪声的振动信号对应的实际工况。

笔者按照第2节所设定支持向量机和卷积神经网络的参数,分别搭建了轴承故障诊断模型。首先，对比了不同负载下原振动信号和显著性序列在两种故障诊断模型中的诊断正确率;然后，比较了利用CNN模型分类时原振动信号和显著性序列达到诊断识别率为100%的训练时间;最后分别在无噪及含噪条件下进行了实验,以验证显著性序列能否提高轴承运行状态诊断率。

笔者发现:(1)针对不同负载下的轴承振动信号,显著性序列可提高诊断准确率,如利用SVM对负载为hp的轴承状态进行诊断时,较原振动信号的诊断准确率提高到99.5%;(2)对于不同负载下的轴承振动信号,显著性序列还可以缩短其训练时间,如在负载为0 hp时,显著性序列训练达到100%的时间为7.6 s,较原振动信号提高了6.7 s;(3)无论是对于无噪信号还是含噪信号,显著性序列均可提高轴承诊断准确率,比如在SNR为-6 dB时,较原始振动信号直接输入卷积神经网络进行分类,显著性序列诊断准确率提高了10.75%。

因此,显著性序列可以有效提高振动信号的分类效果，从而提高轴承振动信号的诊断准确率。

4 结束语

为了提高轴承振动信号在时域方面的诊断准确率,本文提出了一种基于振动信号显著性序列的滚动轴承状态诊断方法;采用支持向量机和卷积神经网络,在美国凯斯西储大学轴承公开数据集上进行了对比实验,验证了显著性序列可有效提高信号在时域上的分类效果。主要结论如下:

(1)与原振动信号相比,显著性序列对无噪声信号的微小频率有放大作用,对噪声信号的频率有抑制作用;

(2)针对不同负载的无噪信号,显著性序列可提高轴承状态诊断准确率,并能缩短模型训练时间;

(3)针对含噪信号,显著性序列可有效提高其诊断准确率。在信噪比为-6 dB时,以支持向量机作为故障诊断模型时,显著性序列的诊断正确率较原始振动信号提高了9%;以卷积神经网络作为故障诊断模型时,显著性序列较原始振动信号的诊断正确率提高了10.75%。

故障诊断主要分为信号处理、特征提取以及故障分类3步,笔者后续将把研究重点放在特征向量的提取上,以提高故障分类的精度,缩短模型的训练时间。