转换信息 分类思考 寻求模型

刘家良

[真题呈现]

例（2020·天津·第25题）已知点A（1，0）是抛物线y=ax2 + bx + m（a，b，m为常数，a ≠ 0，m < 0）与x轴的一个交点.

（1）当[a=1]，[m=-3]时，求该抛物线的顶点坐标.

（2）若抛物线与[x]轴的另一个交点为M（m，0），与[y]轴的交点为C，过点C作直线[l]平行于x轴，E是直线[l]上的动点，F是y轴上的动点，EF=[22].

①当点E落在抛物线上（不与点C重合），且AE=EF时，求点F的坐标;

②取EF的中点N，当m为何值时，MN的最小值是[22]？

[学情分析]

第（1）题：用待定系数法求二次函数解析式并用配方法（或顶点坐标公式）求抛物线顶点坐标. 此问起点低，面向全体.

解：y=x2 + 2x - 3=（x + 1）2 - 4，抛物线的顶点坐标为（-1，-4）.

第（2）题①问：由抛物线与x轴的两交点坐标得到含待定常量a，b，m的两个方程，两个方程组成方程组，但发现其中含有三个待定常量a，b，m. 通过观察，发现此方程组有其特殊性，利用因式分解可得a=1. 然后将b的值用含m的式子表示，这样二次函数的解析式可简化到只含待定常量m的式子. 再将点E的横坐标用含m的式子表示，由勾股定理建立方程求得m值，至此問题的闸门打开.

解：∵抛物线y=ax2 + bx + m经过点A（1，0）和M（m，0），

∴a + b + m=0，am2 + bm + m=0. 整理得（a - 1）（m - 1） = 0，

∵m < 0，∴a=1，∴b=-1 - m. ∴抛物线的解析式为y=x2 -（1 + m）x + m.

根据题意，知点C（0，m）. ∵l[⫽]x轴，∴CE[⫽]x轴，∴点E的纵坐标为m.

令y=m，得x2 -（1 + m）x + m=m. 解得x=0或x=m + 1. ∴E（m + 1，m）.

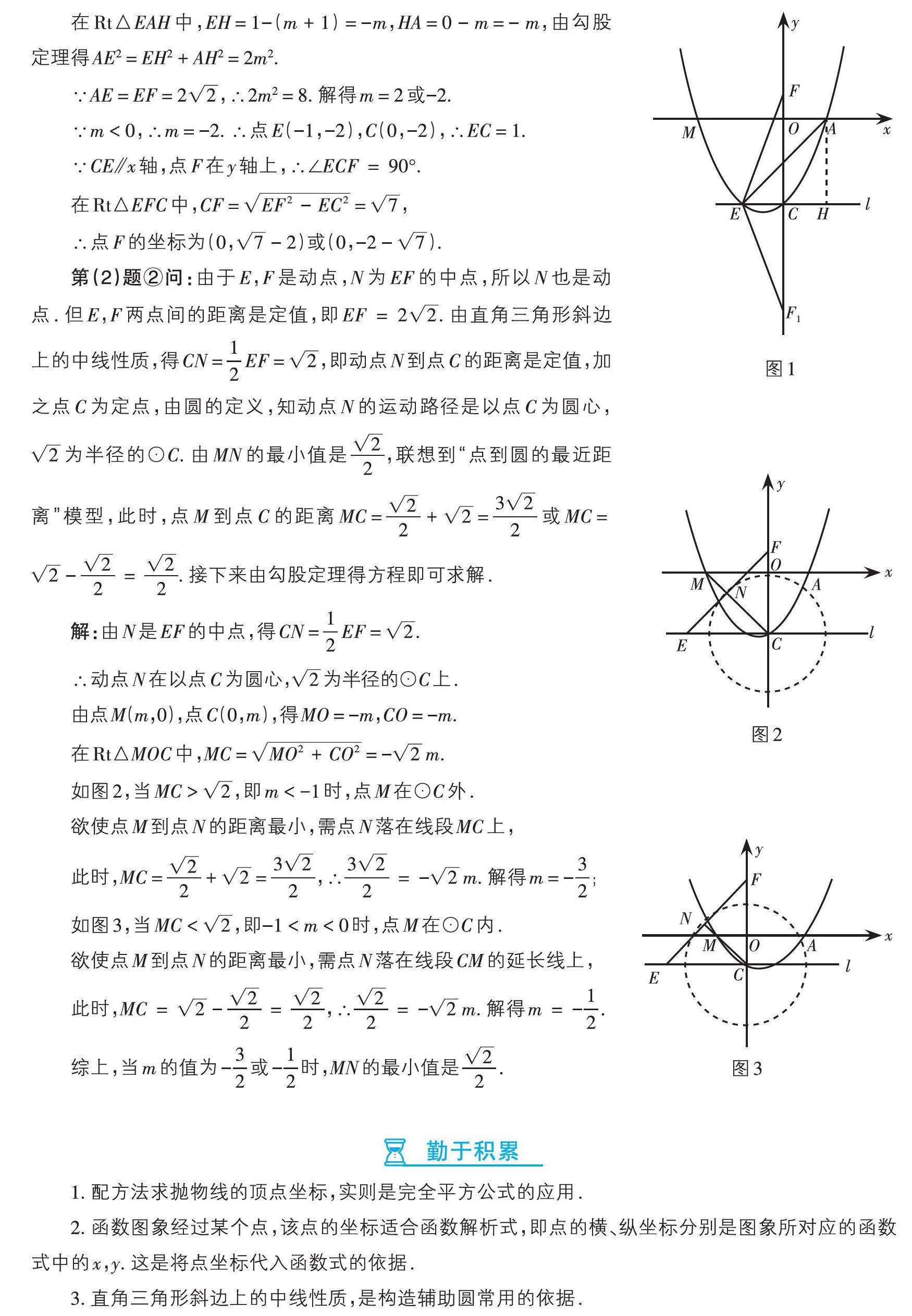
过点A作AH⊥l于点H，如图1. 由点A（1，0），得点H（1，m）.

在Rt△EAH中，EH=1-（m + 1）=-m，HA=0 - m=- m，由勾股定理得AE2=EH2 + AH2=2m2.

∵AE=EF=[22]，∴2m2=8. 解得m=2或-2.

∵m < 0，∴m=-2. ∴点E（-1，-2），C（0，-2），∴EC=1.

∵CE[⫽]x轴，点F在y轴上，∴∠ECF = 90°.

在Rt△EFC中，CF=[EF2-EC2]=[7]，

∴点F的坐标为（0，[7] - 2）或（0，-2 - [7]）.

第（2）题②问：由于E，F是动点，N为EF的中点，所以N也是动点. 但E，F两点间的距离是定值，即EF = [22]. 由直角三角形斜边上的中线性质，得CN=[12EF]=[2]，即动点N到点C的距离是定值，加之点C为定点，由圆的定义，知动点N的运动路径是以点C为圆心，[2]为半径的⊙C. 由MN的最小值是[22]，联想到“点到圆的最近距离”模型，此时，点M到点C的距离MC=[22] + [2]=[322]或MC=[2] - [22] = [22]. 接下来由勾股定理得方程即可求解.

解：由N是EF的中点，得CN=[12EF]=[2].

∴动点N在以点C为圆心，[2]为半径的⊙C上.

由点M（m，0），点C（0，m），得MO=-m，CO=-m.

在Rt△MOC中，MC=[MO2+CO2]=-[2m].

如图2，当MC > [2]，即m < -1时，点M在⊙C外.

欲使点M到点N的距离最小，需点N落在线段MC上，

此时，MC=[22] + [2]=[322]，∴[322] = -[2m]. 解得m=[-32];

如图3，当MC < [2]，即-1 < m < 0时，点M在⊙C内.

欲使点M到点N的距离最小，需点N落在线段CM的延长线上，

此时，MC = [2] - [22] = [22]，∴[22] = -[2m]. 解得m = [-12].

综上，当m的值为[-32]或[-12]时，MN的最小值是[22].

[勤于积累]

1. 配方法求抛物线的顶点坐标，实则是完全平方公式的应用.

2. 函数图象经过某个点，该点的坐标适合函数解析式，即点的横、纵坐标分别是图象所对应的函数式中的x，y. 这是将点坐标代入函数式的依据.

3. 直角三角形斜边上的中线性质，是构造辅助圆常用的依据.