精讲·深剖·慎思

徐秋慧 周丽光 张志军

在辽宁省初中数学学科质量提升暨“聚焦学科课程育人关键问题”教研论坛上，本文作者从学生学习、教师教学、中考命题三个不同角度进行说题分享，引起与会教师的强烈共鸣。

[原题呈现]

如图1，抛物线[y=ax2+bx]（[a>0]）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C，D在抛物线上，[∠BAD]的平分线AM交BC于点M，点N是CD的中点，已知[OA=2]，且OA∶AD = 1∶3.

[（1）]求抛物线的解析式.

（2）F，G分别为x轴、y轴上的动点，顺次连接M，N，G，F构成四边形MNGF，求四边形MNGF周长的最小值.

（3）在x轴下方的抛物线上是否存在点P，使[△ODP]中OD边上的高为[6105]？若存在，求出点P的坐标;若不存在，请说明理由.

（4）矩形ABCD不动，将抛物线向右平移，当平移后的抛物线与矩形的边有两个交点K，L，且直线KL平分矩形的面积时，求抛物线平移的距离是多少.

答案：（1）[y=12x2-4x];（2）四边形MNGF周长的最小值为[122];（3）存在，点P的坐标为（6，-6）;（4）抛物线平移的距离为3个单位长度.

[原题剖析]

一、整体分析抓脉络

该题共4小题：

问题（1）求函数解析式，是常规题;问题（2）求四边形周长的最小值，难度略有提升，但仍属于常见题型. 所以，问题（1）、（2）意在考查基础知识和基本技能.

问题（3）是二次函数与三角形的综合题，难度进一步提升，且需分类讨论，所以它既是本题的第一个难点，也是本题的易错点.

问题（4）是二次函数与四边形的综合题，涉及二次函数图象的平移，需要尝试画出图形，对空间想象能力、数形结合能力、动手操作能力和逻辑推理能力都有要求，无疑是本题的第二个难点.

二、逐题破解究对策

（一）问题（1）

先根据线段的比，求出点D的坐标;然后用待定系数法，通过解二元一次方程组求出抛物线解析式.运用了数形结合思想和方程思想.

（二）问题（2）

因为边MN的长为定值，所以只需求出其余三边之和的最小值.先用轴对称变换，将外侧两条边FM，GN的位置转移，把其余三边之和的最小值问题转化成两点之间的折线最短问题，再依据“两点之间线段最短”的原理求解（如图2）.运用了转化思想.

（三）问题（3）

1. 问题解析

本题有两问，一是“是否存在点P”;二是“如果存在，求出点P”. 其中，第一问需要定性判断;第二问需要定量求解.

2. 条件解析

线索一：“点P在x轴下方的抛物线上”.要用运动变化的观点审视这个条件，由于点D也在x轴下方的抛物线上，因此要分点P在点D的左侧和右侧两种不同位置分别说明.

线索二：“△ODP中OD边上的高为[6105]”.已知三角形的高，不难想到可结合主题干中O，D坐标求其底，于是，很自然地可将这个条件引申为△ODP的面积为[12×210×6105=12].

3. 思路解析

（1）考虑点P在点D右侧，即点P的横坐标大于2小于8的情形.

先估测，当点P运动到右端点E（8，0）时，△ODP的面积是[12×8×6=24]，大于12. 所以，这种情况下点P是存在的，故而需定量地求出点P的坐标.

思路1：从“点P是抛物线上一点”着手.

首先，设点P坐标为[t，12t2-4t ]，[其中2<t<8];然后，结合已知的O，D两点坐标，用t表示出△ODP的面积;再根據符合条件时△ODP的面积是12，列出关于t的方程并求解. 那么，如何用t表示△ODP的面积呢？

方法1：如图3、图4（这种割补的方法不唯一，仅各举一例），由顶点作坐标轴的垂线，将△ODP割补成直角三角形、直角梯形或矩形等已知面积公式的图形.

这种割补直观性强，而且只需利用规则图形的面积公式，同学们使用起来较得心应手. 但其缺点在于，本题中“点P在x轴下方的抛物线上”，位置不确定，而随着点P的位置变化，割补的图形也在变，需要针对点P的不同位置分情况计算. 于是，这种割补在本题中显繁杂.

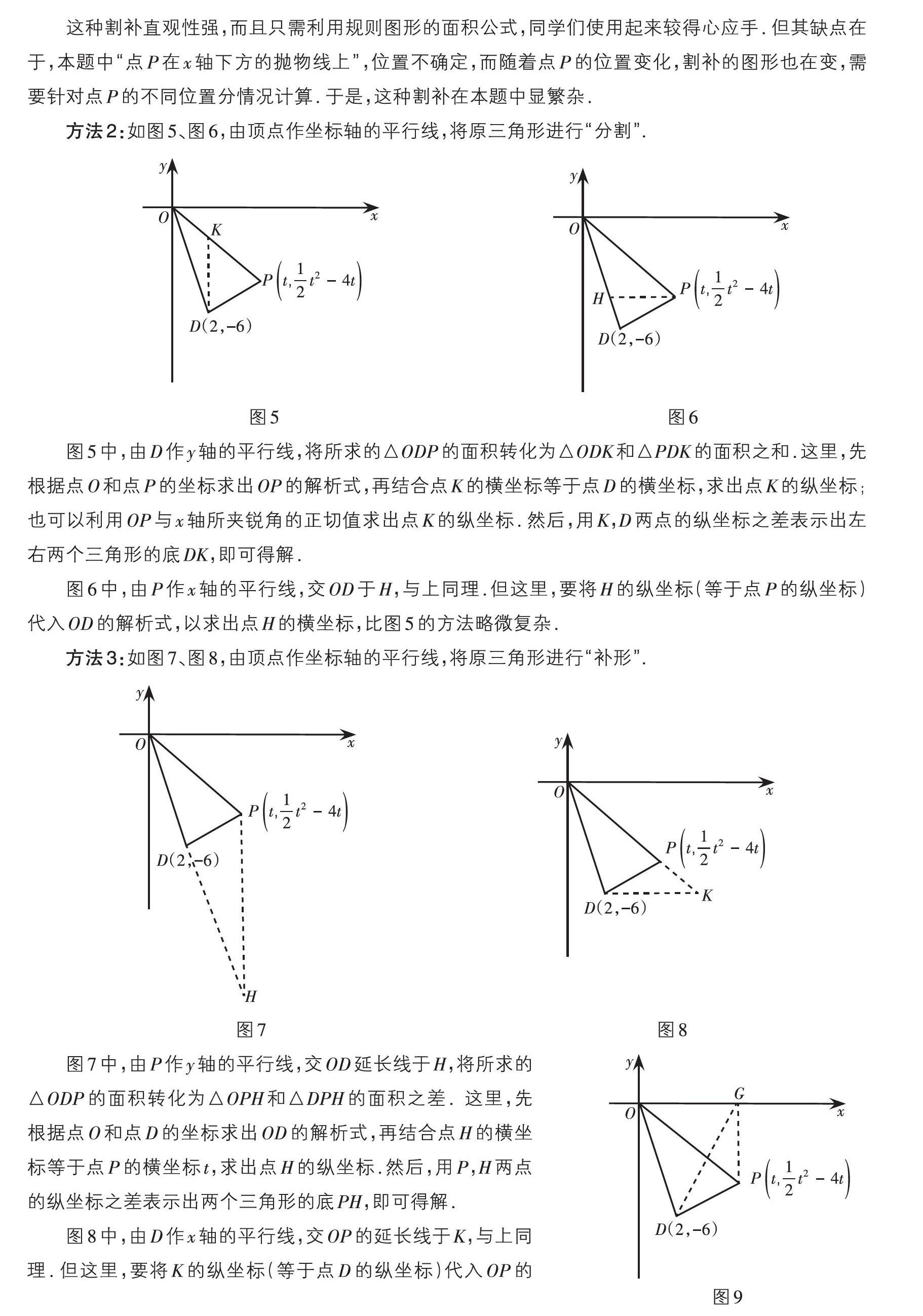
方法2：如图5、图6，由顶点作坐标轴的平行线，将原三角形进行“分割”.

图5中，由D作y轴的平行线，将所求的△ODP的面积转化为△ODK和△PDK的面积之和.这里，先根据点O和点P的坐标求出OP的解析式，再结合点K的横坐标等于点D的横坐标，求出点K的纵坐标;也可以利用OP与x轴所夹锐角的正切值求出点K的纵坐标. 然后，用K，D两点的纵坐标之差表示出左右两个三角形的底DK，即可得解.

图6中，由P作x轴的平行线，交OD于H，与上同理.但这里，要将H的纵坐标（等于点P的纵坐标）代入OD的解析式，以求出点H的横坐标，比图5的方法略微复杂.

方法3：如图7、图8，由顶点作坐标轴的平行线，将原三角形进行“补形”.

图7中，由P作y轴的平行线，交OD延长线于H，将所求的△ODP的面积转化为△OPH和△DPH的面积之差.  这里，先根据点O和点D的坐标求出OD的解析式，再结合点H的横坐标等于点P的横坐标t，求出点H的纵坐标.然后，用P，H两点的纵坐标之差表示出两个三角形的底PH，即可得解.

图8中，由D作x轴的平行线，交OP的延长线于K，与上同理. 但这里，要将K的纵坐标（等于点D的纵坐标）代入OP的解析式，去求点K的横坐标，比图7的方法略微复杂.

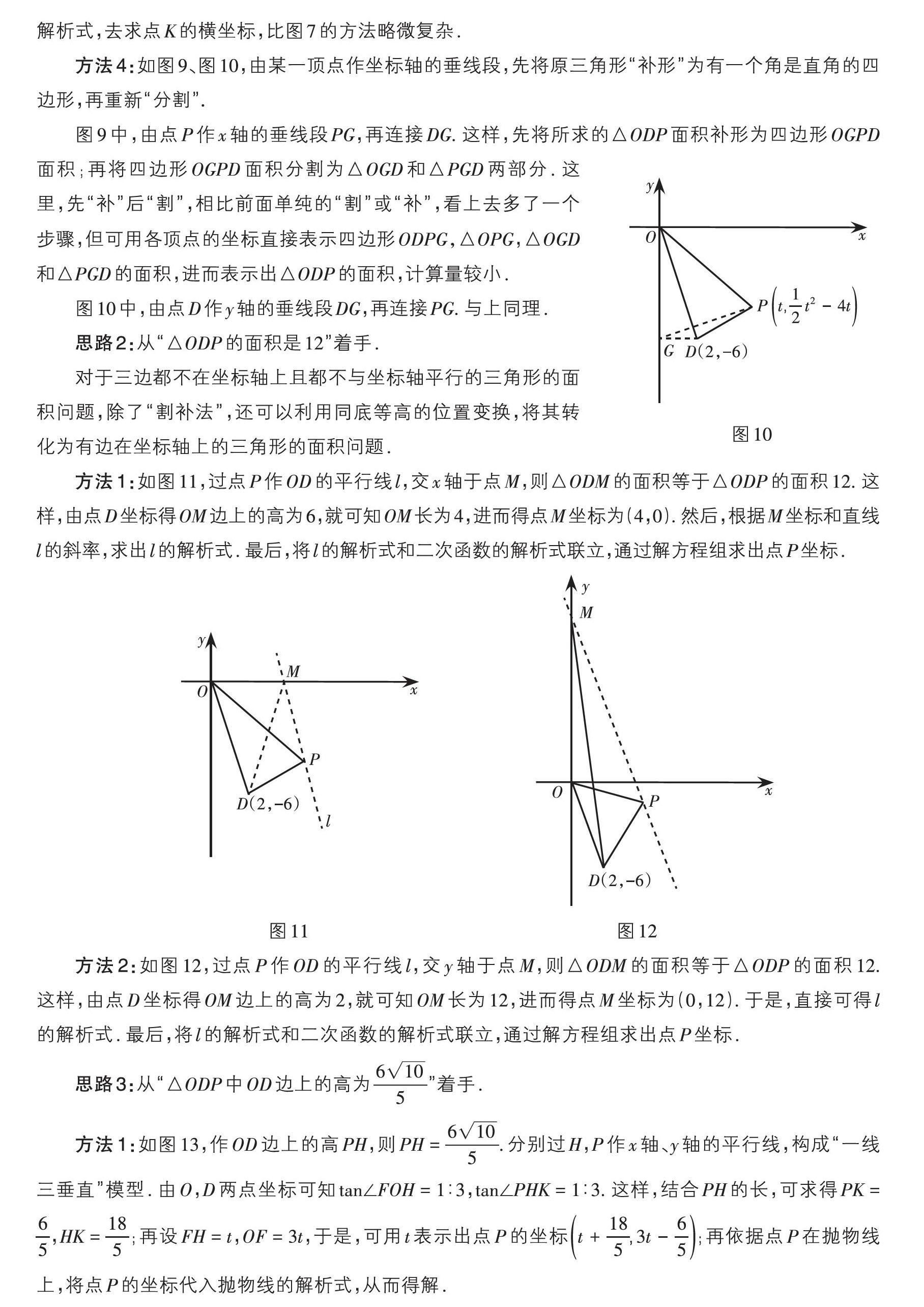
方法4：如图9、图10，由某一顶点作坐标轴的垂线段，先将原三角形“补形”为有一个角是直角的四边形，再重新“分割”.

图9中，由点P作x轴的垂线段PG，再连接DG. 这样，先将所求的△ODP面积补形为四边形OGPD面积;再将四边形OGPD面积分割为△OGD和△PGD两部分. 这里，先“补”后“割”，相比前面单纯的“割”或“补”，看上去多了一个步骤，但可用各顶点的坐标直接表示四边形ODPG，△OPG，△OGD和△PGD的面积，进而表示出△ODP的面积，计算量较小.

图10中，由点D作y轴的垂线段DG，再连接PG. 与上同理.

思路2：从“△ODP的面积是12”着手.

对于三边都不在坐标轴上且都不与坐标轴平行的三角形的面积问题，除了“割补法”，还可以利用同底等高的位置变换，将其转化为有边在坐标轴上的三角形的面积问题.

方法1：如图11，过点P作OD的平行线l，交x轴于点M，则△ODM的面积等于△ODP的面积12. 这样，由点D坐标得OM边上的高为6，就可知OM长为4，进而得点M坐标为（4，0）. 然后，根据M坐标和直线l的斜率，求出l的解析式. 最后，将l的解析式和二次函数的解析式联立，通过解方程组求出点P坐标.

方法2：如图12，过点P作OD的平行线l，交y轴于点M，则△ODM的面积等于△ODP的面积12. 这样，由点D坐标得OM边上的高为2，就可知OM长为12，进而得点M坐标为（0，12）. 于是，直接可得l的解析式. 最后，将l的解析式和二次函数的解析式联立，通过解方程组求出点P坐标.

思路3：从“△ODP中OD边上的高为[6105]”着手.

方法1：如图13，作OD边上的高PH，则PH = [6105].分别过H，P作x轴、y轴的平行线，构成“一线三垂直”模型. 由O，D两点坐标可知tan∠FOH = 1∶3，tan∠PHK = 1∶3. 这样，结合PH的长，可求得PK = [65]，HK = [185];再設FH = t，OF = 3t，于是，可用t表示出点P的坐标[t+185，3t-65];再依据点P在抛物线上，将点P的坐标代入抛物线的解析式，从而得解.

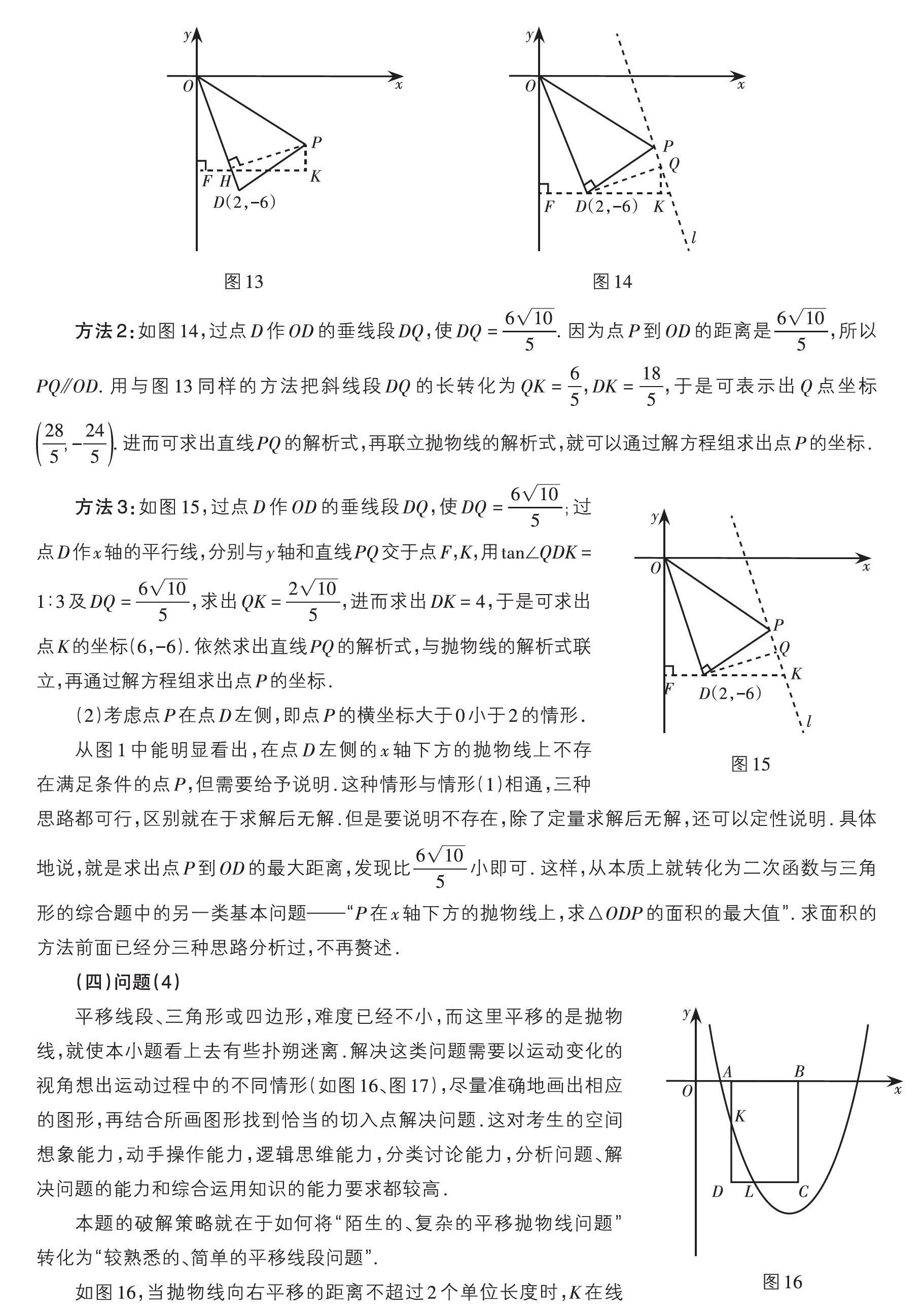
方法2：如图14，过点D作OD的垂线段DQ，使DQ = [6105]. 因为点P到OD的距离是[6105]，所以PQ[⫽]OD. 用与图13同样的方法把斜线段DQ的长转化为QK = [65]，DK = [185]，于是可表示出Q点坐标[285，-245]. 进而可求出直线PQ的解析式，再联立抛物线的解析式，就可以通过解方程组求出点P的坐标.

方法3：如图15，过点D作OD的垂线段DQ，使DQ = [6105];过点D作x轴的平行线，分别与y轴和直线PQ交于点F，K，用tan∠QDK = 1∶3及DQ = [6105]，求出QK = [2105]，进而求出DK = 4，于是可求出点K的坐标（6，-6）. 依然求出直线PQ的解析式，与抛物线的解析式联立，再通过解方程组求出点P的坐标.

（2）考虑点P在点D左侧，即点P的横坐标大于0小于2的情形.

从图1中能明显看出，在点D左侧的x轴下方的抛物线上不存在满足条件的点P，但需要给予说明.这种情形与情形（1）相通，三种思路都可行，区别就在于求解后无解.但是要说明不存在，除了定量求解后无解，还可以定性说明. 具体地说，就是求出点P到OD的最大距离，发现比[6105]小即可. 这样，从本质上就转化为二次函数与三角形的综合题中的另一类基本问题——“P在x轴下方的抛物线上，求△ODP的面积的最大值”. 求面积的方法前面已经分三种思路分析过，不再赘述.

（四）问题（4）

平移线段、三角形或四边形，难度已经不小，而这里平移的是抛物线，就使本小题看上去有些扑朔迷离.解决这类问题需要以运动变化的视角想出运动过程中的不同情形（如图16、图17），尽量准确地画出相应的图形，再结合所画图形找到恰当的切入点解决问题.这对考生的空间想象能力，动手操作能力，逻辑思维能力，分类讨论能力，分析问题、解决问题的能力和综合运用知识的能力要求都较高.

本题的破解策略就在于如何将“陌生的、复杂的平移抛物线问题”转化为“较熟悉的、简单的平移线段问题”.

如图16，当抛物线向右平移的距离不超过2个单位长度时，K在线段AD上，L在线段CD上. 此时，矩形在直线KL下方的部分是△KDL，其面积不足矩形面积的一半，所以这种情形下的直线KL不能平分矩形面积.

如图17，当抛物线向右平移的距离超过2个单位长度且不超过4个单位长度时，K在线段AB上，L在线段CD上.此时，虽然向右平移抛物线会使直线KL位置发生变化，但它在随抛物线做同样的平移，所以其倾斜程度不变，始终与OD平行. 这样就会发现，本问虽是平移抛物线的问题，但其实质就是平移线段OD的问题.

设抛物线向右平移m个单位长度，则KL就是OD向右平移了m个单位长度的线段，故K（m，0），L（2 + m，-6），可求出直线KL的解析式. 再根据矩形的中心对称性可知，当且仅当直线KL经过对角线的交点（即AC的中点）时平分矩形的面积，将AC的中点H的坐标代入KL的解析式，即可求出m的值，问题得解. 也可以先证得AC的中点H恰为KL的中点，由中点坐标公式列出方程，问题得解.

当然，问题（4）还可以根据“运动的相对性”，视抛物线不动，将矩形向左平移——矩形向左平移几个单位长度时符合条件，就是抛物线向右平移几个单位长度时符合条件.这种思路与上述做法相通，不再赘述.

三、合理猜想寻突破

对于压轴题的最后一问或最后两问，大多数同学常感困惑不已.其实，只要准确作图，大胆猜想，往往就有意外收获，这道题也不例外.

回看问题（3），如图18，观察图中的点，再标出已知点的坐标看一看，不难发现△OCD的面积恰好是12，也就是说△OCD就是满足OD边上的高为[6105]的三角形，而且点C也在抛物线上. 这种种迹象都在告诉我们，点C恰是我们要求的点P的位置. 这样一来，无需添加其他辅助线，无需大量计算，经过简单说理即可得解.

再看问题（4），如图19，考虑平移过程中的特殊位置，不难发现：当抛物线向右平移2个单位长度时，K与A（2，0）重合，L在DC中点（4，-6），直线KL将矩形分为左右面积比为1∶3的两部分;当抛物线向右平移4个单位长度时，K在AB中点（4，0），L与C（6，-6）重合，直线KL将矩形面积分为左右面积比为3∶1的两部分. 显然，由矩形的对称性可知，恰在这两次平移的中间位置，即将原抛物线向右平移3个单位长度时，直线KL平分矩形的面积，问题得解.