杨氏双缝干涉光程差近似计算问题在教学中的探讨*

刘婷婷，张 勇，闫文宇，苏新皓

(晋中信息学院，山西 晋中 030800)

1 引言

1801年最早由托马斯·杨提出并成功利用实验的方式利用单一光源获得相干光证明光的波动性质。杨氏双缝干涉实验对波动光学的发展产生了重要的意义，同时也是大学物理课程中波动光学部分的重点内容。在理论分析光的干涉现象时，光程差的处理成为了研究干涉现象的主要问题。大部分的光学教材中，对双光束干涉中光程差的近似计算问题只进行了简单说明，本文就杨氏双缝干涉实验中在处理光程差近似计算中存在的问题进行分析并给出较为合理的光程差近似计算方法。

2 经典教材中光程差近似计算处理方法

本文重点参考三本经典教材进行分析说明。光源发出的光照射单缝S，S1和S2是两个相距为d的狭缝，O1为两狭缝的中心，根据惠更斯原理，从狭缝S1、S2发出的光可以作为新的子波源向外辐射球面波。距离双缝D处有一接收屏，O为接收屏的中心，在屏幕上任取一点P，x为P到O点的距离。设P到S1的几何距离为r1，P到S2的几何距离为r2。

综合文献1-3 对光程差的处理采用如下三个近似条件：

傍轴条件：D﹥﹥d，D﹥﹥x，；

θ角很小，sinθ≈tanθ；

图1 杨氏双缝干涉实验原理图

图2 杨氏双缝干涉实验光程差近似计分析图

3 杨氏双缝干涉实验光程差的误差分析

代入上式可得误差约为10-7m，仍然不满足小于/2λ。

下面分析上述近似中的(1)和(2)产生的误差。例如取D≈1m，d≈10-3m，x=5cm，λ=500nm，则

从计算结果可以看出dsinφ≈dtanθ是不合理的，它带来的误差与可见光的波长量级相同。

这一不妥当的近似方法是由于该条件的满足不仅应该满足傍轴条件（b2﹤﹤D2，x2﹤﹤D2），还应同时满足远场条件才能成立，该条件在文献1 中进行了说明。

4 杨氏双缝干涉实验精确计算与近似计算

杨氏双缝干涉光程差的精确计算公式为：

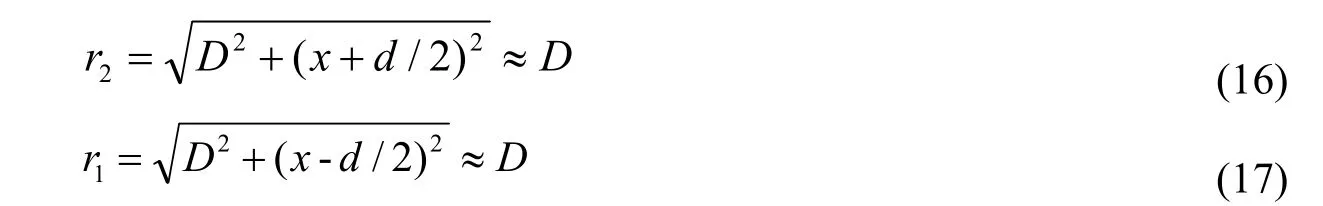
用r2+r1=2D代入光程差公式，可得

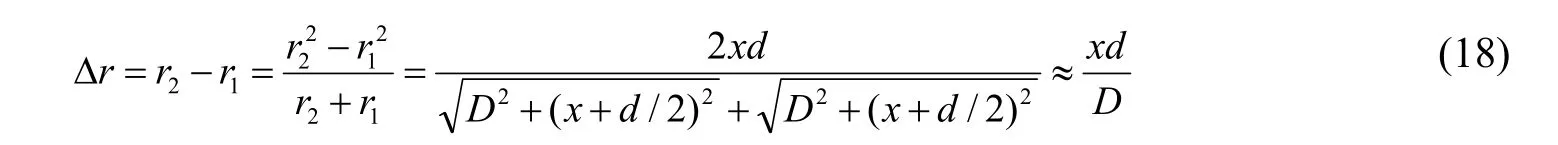
该种近似方法不涉及复杂的数学公式，且近似条件符合实验基本条件。

5 小结

上述对杨氏双缝干涉实验光程差的处理进行了反思，对教材中没有进行详细说明的近似处理问题进行了详细的数学计算。利用合理的近似，对实验中光程差的处理提出了新路径，摒弃复杂的数学推导，方便学生理解。