洛伦兹变换的数学形式及其物理学意义新探讨

郭德强

（国家电网抚顺县供电公司，辽宁 抚顺 113006）

1 引言

洛伦兹变换是狭义相对论的数学基础，本文通过对洛伦兹变换进行数学剖析，给出其全新的数学形式并赋予其全新的物理学意义。

2 洛伦兹变换在v ﹤﹤c 条件下并不能约化为伽利略变换

通常认为，当v﹤﹤c时，洛伦兹变换

可约化为伽利略变换

然而，在有关教材和著作中，对于这种结论并无具体证明过程，只是一语带过而已。笔者通过研究发现，当时，洛伦兹变换中的第一方程和第四方程的近似解并非伽利略变换。具体证明过程如下：

若设v=0.01c，则有

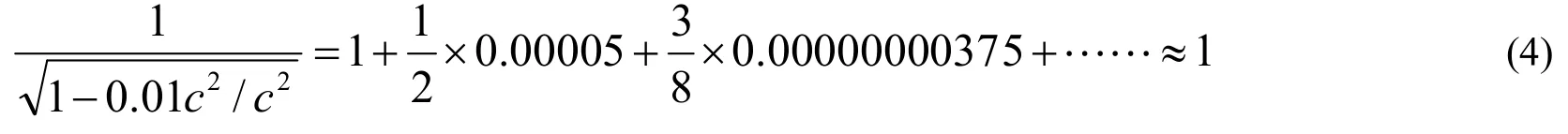
由此可见，当v﹤﹤c时，因为必然有

所以洛伦兹变换中的第一方程和第四方程在v﹤﹤c条件下的近似解应该为

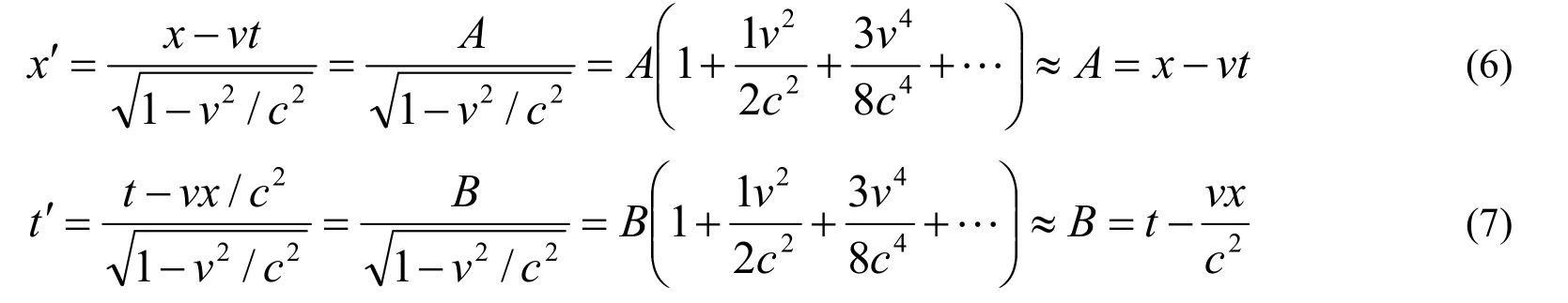
事实上，洛伦兹在1895年发表的论文《运动物体中的电和光现象理论研究》中给出的洛伦兹变换的最初数学表达形式[1,2]就是

3 在洛伦兹变换中y ′=y、z ′=z是多余的方程

将(1)中各方程代入

依次判断，在洛伦兹变换中，像y′=y、z′=z这种不证自明的方程，应该完全属于可多可少、可有可无的多余且无用的方程。

因此，洛伦兹变换应该只是由

这两个核心方程组成的，而且洛伦兹变换还应该有另一组方程，即

“新秩序”时期印尼的政治经济等方面相对稳定，语言规划得以重视，政府提倡“优先印尼语，维护地方语，掌握外国语”，再次巩固了印尼语的地位。苏哈托政府试图同化华人，华人作为一个民族没有得到国家的认可，华语不论是作为华人的民族共同语还是印尼的地方语也均未获得官方认可。

4 洛伦兹变换与多普勒原理的同一性

狭义相对论给出光源和接收器在同一直线上相互接近或远离的多普勒原理频率关系式

根据λ=c/f、λ′=c/f′、T=1/f、T′=1/f′可以相应地得到多普勒原理波长关系式和周期关系式

对(23)、(24)进行数学变形，可以得到

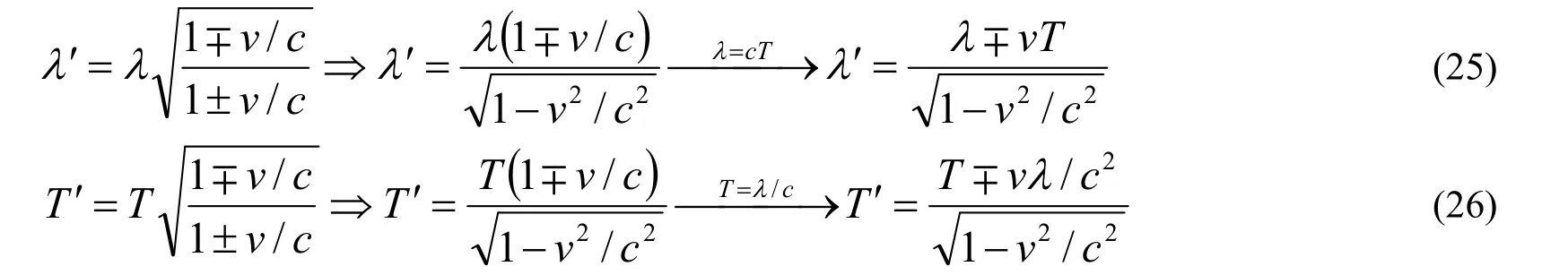
因为多普勒原理可以写为

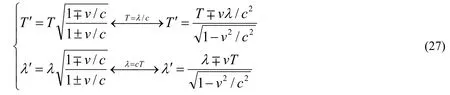
所以洛伦兹变换可以写为

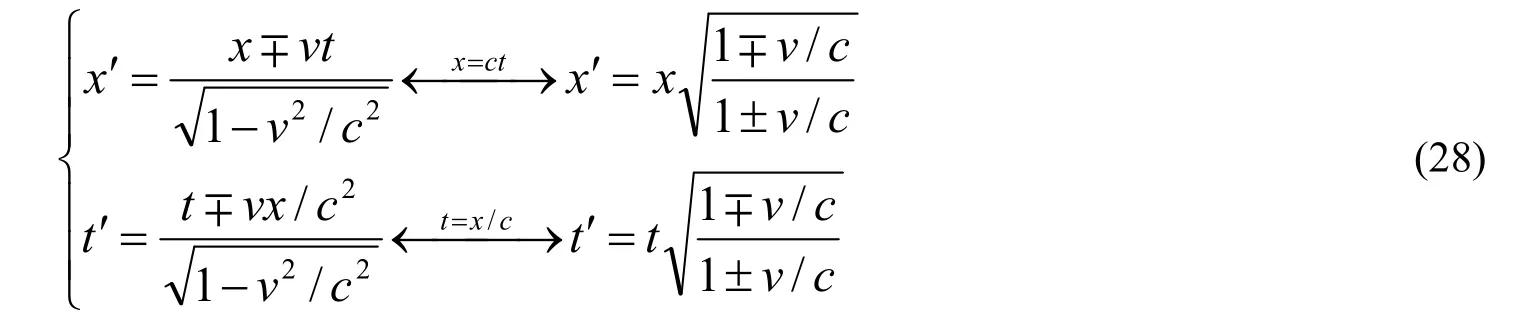
多普勒原理与洛伦兹变换之间在数学形式上相同并非巧合，而是必然，因为二者描述的是同一对象——平面光波在互作匀速直线运动的两个坐标系之间的传播。

5 洛伦兹变换与平面波波动方程的协变

若平面光波在坐标系K中沿着坐标轴X传播，则平面光波波动方程在坐标系K中应该表示为

根据洛伦兹变换可以得到

将(30)、(31)代入(29)，有

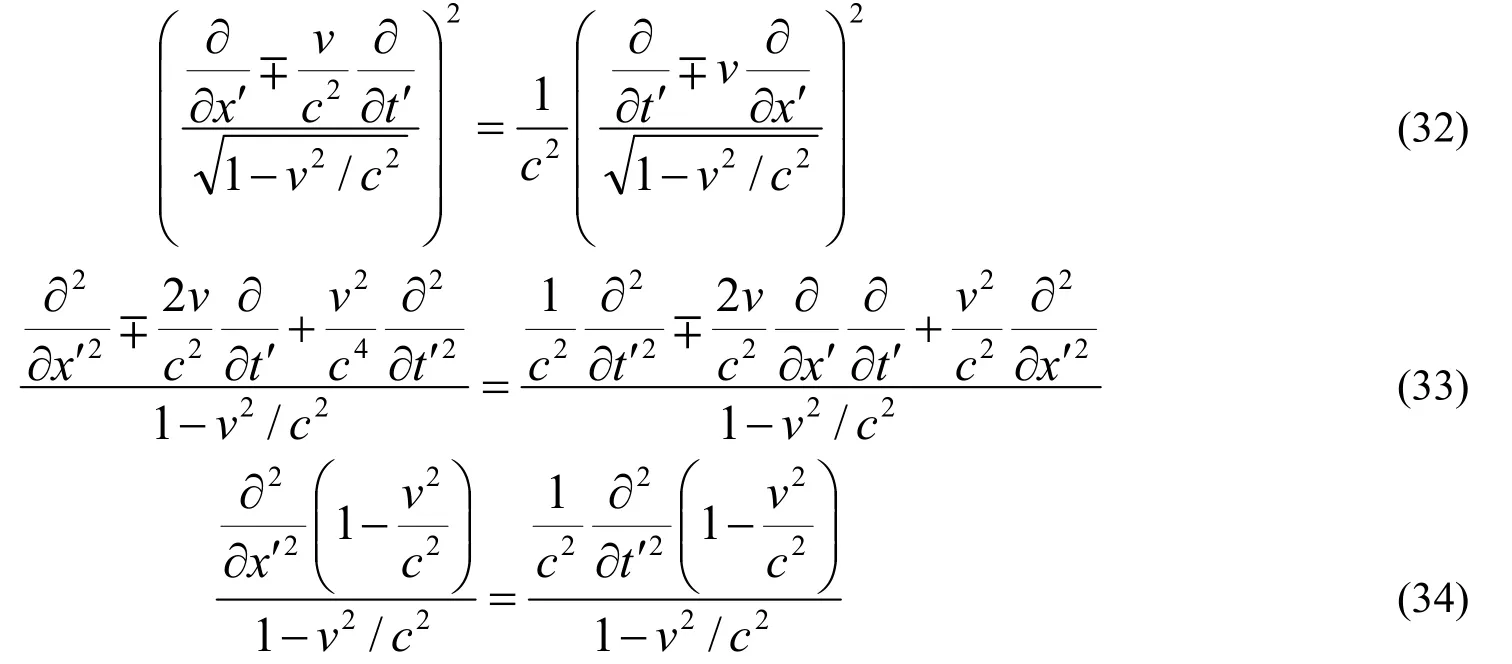
于是最后得到平面光波从坐标系 传播到坐标系，在坐标系 中的平面光波波动方程为

当平面光波从坐标系K传播到与其互作匀速直线运动的坐标系K′时，满足平面光波波动方程在这两个坐标系中数学形式相同恰恰是洛伦兹变换应该具有的物理学意义。若将洛伦兹变换中的光速c用声速u替换，也可以使得平面声波波动方程在互作匀速直线运动的两个坐标系中数学形式相同。所以洛伦兹变换的唯一物理学意义应该是只能满足平面波波动方程在两个坐标系之间数学形式的协变。