关于随机变量独立性的一个反例研究

刘 蕾

(上海对外经贸大学)

0 引言

在很多概率论的定理、结论(如分布的可加性)中，独立性都是前提之一.若随机变量的独立性不成立，则众多结果将难以保证.“概率论与数理统计”中都有这样的一个结论：随机变量X,Y不独立，但其函数可能独立，也有可能不独立.大多《概率论与数理统计》教材都是采用如例1给予说明的.

例1 设二维随机变量X,Y的联合密度函数为：

则有：(1)X,Y不独立；(2)X与Y2独立，X2与Y独立；(3)X2与Y2独立.

该例最早由刘锦萼和张尚志于1984年在文献[1]中提出的，之后的概率统计的教科书、反例书大都是采用这个例子.后来，沈子曦和徐晓岭在文献[2]中针对此例进行了多方面的推广.那么有没有其它用来说明这一问题的反例呢？如果有，那会有什么特殊的结论呢？

该文将以此为出发点，对样本容量为2的自由度为n的t分布总体的样本的次序统计量的性质进行系统性总结研究.

1 随机变量独立性中一个反例的深入分析

下面通过样本容量为2的自由度为n的t分布样本说明这一结论，并作进一步拓展分析.

设总体X服从自由度为n的t分布，记为X～t(n)，其密度函数和分布函数分别为：

设X1、X2是来自总体X的容量为2的一个简单随机样本，X(1)≤X(2)为其次序统计量，记

定理1Y1与Y2既不独立也不同分布.

证明对-∞y1)=1-P(X1>y1,X2>y1)=2FX(y1)-[FX(y1)]2

fY1(y1)=2fX(y1)-2FX(y1)fX(y1)=2fX(y1)[1-FX(y1)]

对-∞

fY2(y2)=2FX(y2)fX(y2)

另一方面，对-∞

+∞,

FY1,Y2(y1,y2)=P(Y1≤y1,Y2≤y2)=P(Y2≤y2)-P(Y1>y1,Y2≤y2)=[FX(y2)]2-P(X1>y1,X2>y2,X1≤y2,X2≤y2)

注意到：

若y2y1,X2>y2,X1≤y2,X2≤y2)=0

则

FY1Y2(y1,y2)=[FX(y2)]2

若y2≥y1时，P(X1>y1,X2>y2,X1≤y2,X2≤y2)=P(y1

则

FY1,Y2(y1,y2)=[FX(y2)]2-[FX(y2)-FX(y1)]2=2FX(y1)FX(y2)-[FX(y1)]2

fY1,Y2(y1,y2)=2fX(y1)fX(y2),y1≤y2

易见：Y1与Y2是不独立的.

评注：(1)次序统计量X(1)与X(2)有不同的分布，且X(i)与Xi，i=1,2服从于不同的分布；(2)虽然X1与X2独立同分布，但X(1)与X(2)既不独立也不同分布.

定理2Z1与Z2独立同分布.

即

Z1～F(1,n)

对z2>0，FZ2(z2)=P(Z2≤z2)=

即

Z2～F(1,n)

另一方面，对z1≥0,z2≥0，

FZ1,Z2(z1,z2)=P(Z1≤z1,Z2≤z2)=

注意到：

则

由此

综上：

于是得：Z1与Z2独立同分布.

另外，

F-Y1(y1)=P(-Y1≤y1)=P(Y1≥-y1)=P(X1≥-y1,X2≥-y1)=[1-FX(-y1)]2=[FX(y1)]2

F-Y2(y2)=P(-Y2≤y2)=P(Y2≥-y2)=1-P(Y2≤-y2)=1-[FX(-y2)]2=2FX(y2)-[FX(y1)]2

所以，X(1)和-X(1)具有不同的分布，X(2)和 -X(2)也具有不同的分布.但是，X(1)和-X(2)以及X(2)和-X(1)是同分布的.

定理3Y1与Y2-Y1不独立.

证明由于(Y1,Y2)的联合密度函数为：fY1,Y2(y1,y2)=2fX(y1)fX(y2),y1≤y2.

fX(u+v),-∞

又fU(u)=2fX(u)[1-FX(u)]

显然，fU,V(0,1)≠fU(0)fV(1)

于是可以看到：Y1与Y2-Y1是不独立的.

评注：Y1与Y2-Y1对应的是样本容量为2的t(n)分布次序统计量的间隔，该间隔彼此之间是不独立的.而若是指数分布总体，次序统计量的间隔是独立的.

定理4Y1与Z2不独立，Y2与Z1也不独立.

证明(1)Y1与Z2的联合分布：对-∞

FY1,Z2(y1,z2)=P(Y1≤y1,Z2≤z2)=

注意到：

则

则

于是得：Y1与Z2是不独立的.

(2)Y2与Z1的联合分布：对-∞

+∞，z1≥0,

FY2,Z1(y2,z1)=P(Y2≤y2,Z1≤z1)=

注意到：

则

则

于是得：Y2与Z1是不独立的.

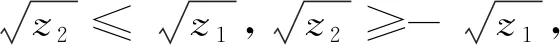
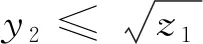
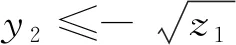
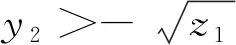
2 结论