基于大数据的中小微企业信贷风险评估和信贷策略研究*
陈春照,谢 睿,查婧怡,朱家明
(安徽财经大学)
0 引言
随着国家政府不断深入推动经济建设进程,经济的稳定增长成为中国的首要目标,尤其体现为对中小微型企业的发展的政策扶持与改进.国家和政府对中小微企业的融资和授信政策,促进了银行在中小微金融领域的创新,解决了中小微企业的资金需求.而新的中小微企业的信贷政策放开后,可能会对银行的资产质量以及收益产生不良影响,但同样也会在一定程度上改善经济的稳定均衡增长,从而促进创新、增强就业、改善民生.因此,应就中小微企业的信贷风险评估体系的提出进行具体研究,从而给出具体的中小微企业信贷时的贷款额度、利率、期限以及是否放贷等信贷策略,以实现达到银行资产质量最优和解决中小微企业融资难题的目标.
杜侃倩对银行个人信贷机制做了较深入的研究,从银行的角度将风险分类为10小类,同时通过考虑个人信贷指标体系以及风险的等级,构建了个人信贷综合评价体系[1].同时,就民生银行及其南京分行基本情况,以8位住房货款申请人进行风险的评价和货款决策过程进行了实证检验.但是由于风险等级的主观性,未就放贷的具体政策进行分析和计算,只是宏观上的把控.魏青在指出现有货款定价的利率调整的不合理性和非精细化的定价基础上,借鉴国内外文献增加收益-风险目标的Racon货款定价方法,其中收益不再是单一的净资产收益率,风险不再是简单的信用风险、市场风险.这种制定信贷利率的策略虽然更加合理,但是要对信贷策略做出决策时,不仅要考虑利率,还要考虑额度和期限等一系列指标[2].郭战琴在现代单笔信贷决策理论的理论框架下,提出多目标贷款组合的决策方法,并通过几何方法对该多目标决策模型求解[3].一方面,多目标贷款组合解决了单个目标的不足,另一方面,使得银行能充分考虑到受限客户的需求.其次,由于银行贷款面临的收益和风险的不确定性,运用了区间数的相关理论,提出基于区间数的不确定性组合信贷决策方法,但是,没有对比分析其他典型的贷款组合方法,因此,具有一定的片面性.总而言之,现有的文献或多或少都有其不足之处,需要加以完善.
1 中小微企业信贷风险评估体系的构建
1.1 指标体系构建
考虑数据的溯源性以及可获得性并结合相关信贷理论,把这些因素细分为5个方面,分别是资金流量因素、供求关系因素、上下游企业交易活力因素、企业的营业利润因素以及信用水平因素,以建立信贷风险评估指标体系[4].
为了更具体地分析并解决问题,将这5个方面继续细分,决定选取进销项总金额、进销项总税额、进销项单数、总利润、作废、负数发票比例等14个量作为评价指标,如图1所示.
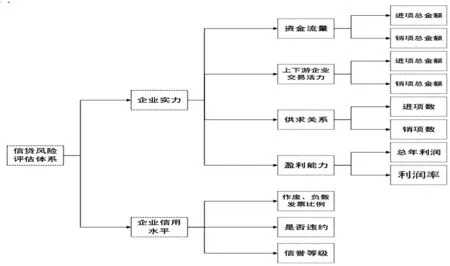
图1 企业风险评估指标体系
1.2 数据来源与假设
该文数据来源于2020年全国大学生数学建模竞赛C题提供的123家有信贷记录企业的相关发票数据以及302家无信贷记录企业的相关发票数据.为了便于解决问题,该文的研究过程和结论建立在以下假设成立的基础上:(1)假设Excel、Python处理筛选数据没有偏差,真实且有效;(2)假设企业具备一定的突发情况应对能力;(3)假设除了选定的指标体系,其他因素对风险评估和决策影响较小;(4)假定最优贷款额度应与企业整体保持相同的变化率[5].
2 123家历史企业的信贷风险评估及信贷策略决策
2.1 研究思路
首先通过主成分分析确定更规范的指标体系后,再采用灰靶决策模型,通过求解一般企业与标准企业的灰靶距离,做出是否放贷与放贷次序的决策策略.最后,采用RAROC 贷款定价方法,考虑成本与风险,对各企业贷款的利率、额度、期限等进行决策.
2.2 模型的建立与求解
模型Ⅰ——PCD-GTD模型(细化指标体系,确定是否放贷和初步放贷的次序)
(1)模型的准备
数据的处理和指标设计:删去信誉等级为D的企业数据,默认其不具备信贷资格;信誉等级、是否违约进行赋值法处理,即信誉等级指标分别赋值“A”—3、“B”—2、“C”—1;是否违约指标分别赋值“是”—1、“否”—0;
(2)模型的建立与求解
根据数据处理筛选分析结果,考虑到信贷风险评估指标体系中存在的一系列线性相关现象,公司上下游企业的活力与供求关系(进销项数与进销税额等)、企业信用水平的信誉等级与违约是否等存在较大的线性相关关系等.因此,有必要对其进行主成分的提取,从而使得评价指标体系更能反映实际风险评估状况.基于此,利用附件2017~2019年的相关度量评价指标(其中加入2个指标,违约次数,违约金额,便于进行靶心的提取和风险分级,)以此为基础进行数据的无纲量化以及主成分的提取,包括特征值与权重[1],具体计算结果见表1.
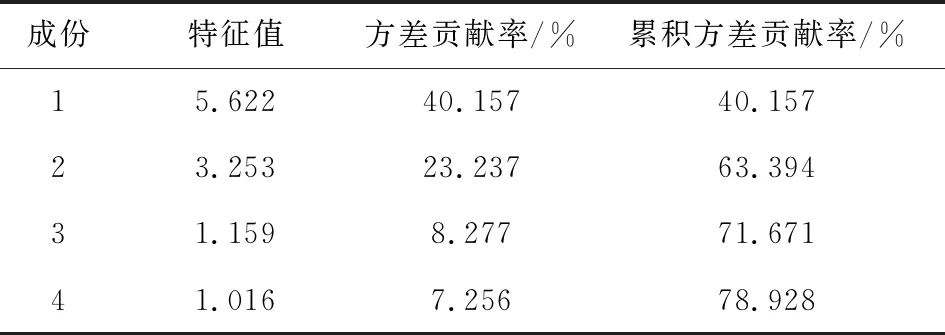
表1 信贷风险PCA分析的总方差解释率表
通过历史数据计算可得到上述主成分及其因素构成,由表1可知,4个主成分的方差贡献率分别为40.157%、23.237%、8.277%、7.256%,提取的4个主成分解释了整体指标78.928%的信息,由此,上述主成分能够有效解释整体,进而可用其对企业进行客观的风险评估决策.随后计算得到标准化后的123家企业各主成分特征值见表2,为下面进一步的风险等级评估以及信贷策略的确定提供了指标处理和模型计算的依据.
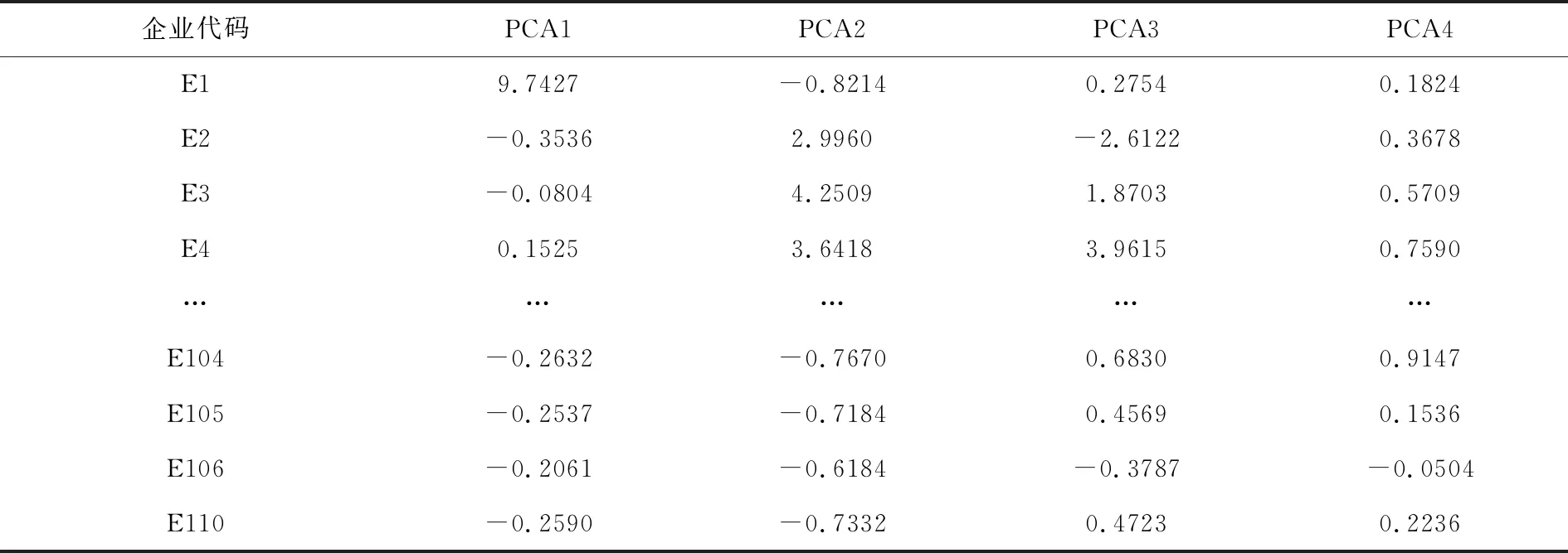
表2 企业各主成分特征值
确认主成分后,假设银行信贷总额度固定且充裕,建立中小微企业信贷的灰靶决策模型,考虑额度有限条件下贷款人风险排序和决策问题.各中小微企业为一个局势,其中风险评价是事件,事件下的可取对策是“是否放贷”.
针对“风险评价”事件,存在如下局势:
Sij=(ai,bj)=(贷款,企业i)
(1)
需要对99家中小微企业的局势是否满足银行贷款风险要求进行排序和放款决策.
根据表2即可得到中小微企业相关局势的主成分,以企业E1局势为例:
S11=(9.7427,-0.8214,0.2754,0.1824)
(2)
选取各指标最优值设定标准信贷企业作为靶心企业, 因为其来自整个数据量的最优值,因此其相关主成分为:
r0=(1,1,1,1)
(3)
运用灰靶决策模型分别计算所有企业的灰靶距离,作为风险量化值.以E1、E2、E3为例,3个企业的信贷风险加权靶心距为:
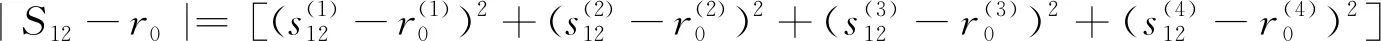
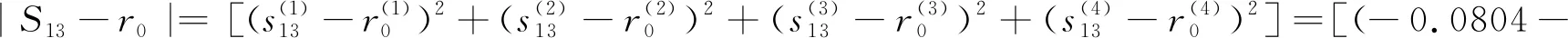
(4)
根据加权灰靶距离根据距离越小,风险相对较低的原则,分析出其是否放贷和放贷次序.根据上文计算的靶心距结果如图2所示,其中风险由低到高的具体排序顺序为:企业1企业2企业3.因此,当银行信贷额度固定时,可根据额度参考以上顺序依次放贷.
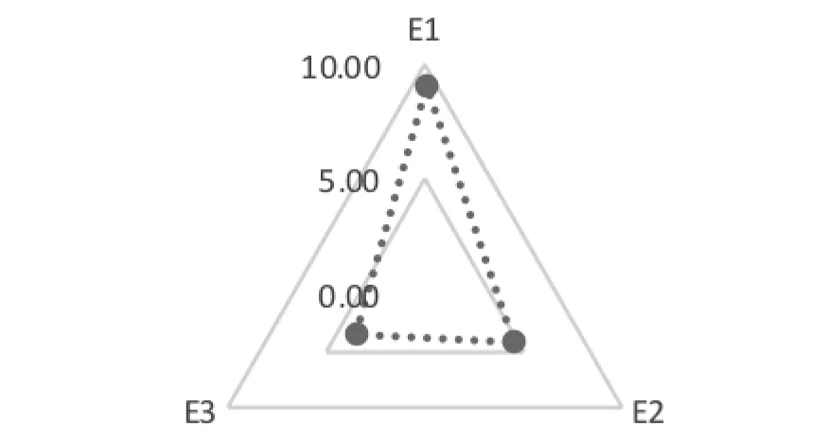
图2 企业靶心距离图
最终计算得99家中小微企业的信贷风险量化值,对其进行排序见表3.按灰靶距离由小到大排列为E23、E21、E6、E75…,整体风险值平均数为2.63,四分位数为2.16、2.39、2.66,在银行对信贷不同风险偏好下,控制不同数量的中小微企业放贷.

表3 信贷风险量化值
模型Ⅱ—RAROC 贷款定价模型(计算出确定的信贷策略的相关指标)
初步确定是否放贷和放贷次序后,就可放贷的企业采用RAROC 贷款定价模型,计算出其具体的放贷策略(放贷利率、额度、年限).定义资金回报率为风险调整后的收入与风险调整后的资本之比,作为衡量标准对银行的信贷利率进行定价.
(1)模型的准备
建立信贷策略决策的数学模型:
Q=r·M·u+(r+1)·M·v
(5)
P=r·M+M·a+(1-u)·r·M
(6)
其中,Q为风险成本,P为综合考虑银行、企业的信贷利润,r为贷款年利率,M为贷款额度,u为与r对应的客户流失率,v为各企业违约风险率,由风险量化值归一化处理得到,a为各企业利润率.假定银行在制定信贷年利率时,必须考虑信贷的资本成本和风险成本,使得银行能够避免因为企业违约所带来的风险损失,以及客户流失所带来的未来损失,保证贷款业务盈利能力的最大化.
(2)模型的建立与求解
以来自不同信誉等级的3个企业E23、E6、E75为例,说明制定最优贷款策略的决策过程.企业信誉评级为B,在控制一组r与u对应不变的情况下,调整范围在10~100万元的贷款额度,首先以信贷利润最大为目标,求得最优利率,再在此利率下做出某一风险偏好情况的最终贷款策略,如图3所示.
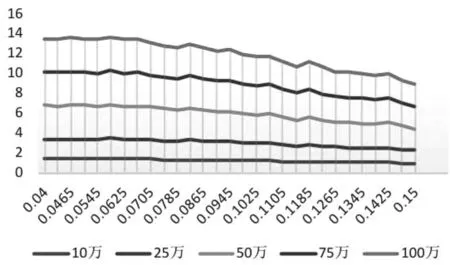
图3 E23企业不同额度利率下的P、Q差值
贷款额度不变时,银行信贷利润随利率增大整体呈下降趋势,当r=0.0585时,利润达到最大,为最优利率;由于额度越大,信贷风险越大,如图4所示,例如若银行风险损失值偏好小于1.5万,则最优贷款额度为约84万.
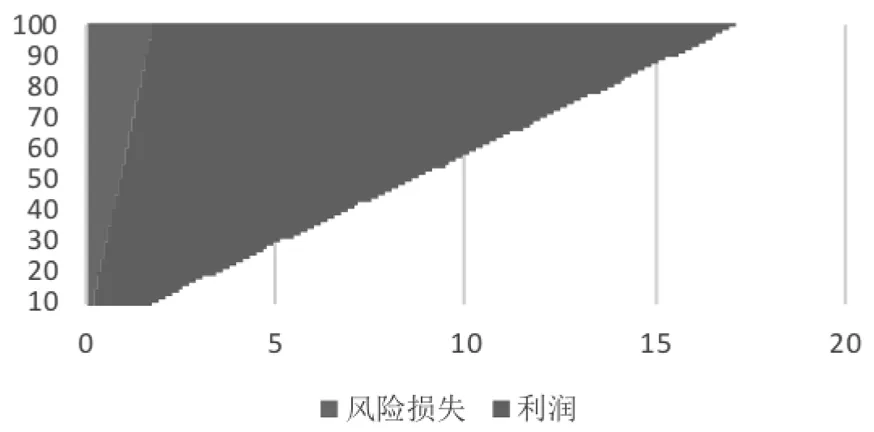
图4 E23企业不同额度的风险损失与信贷利润
同理可得,E6企业(信誉等级为A)和企业E75(信誉等级为C)的最优利率分别为0.0465和0.0585,若银行风险损失值偏好小于1.5万,则最优贷款额度分别约为53万和43万如图5、6所示.
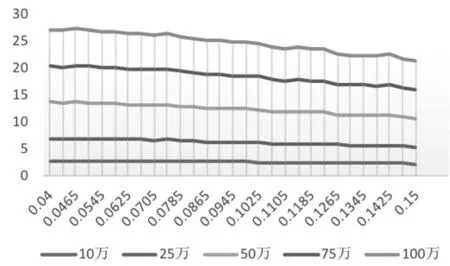
图5 E6企业不同额度利率下的P、Q差值
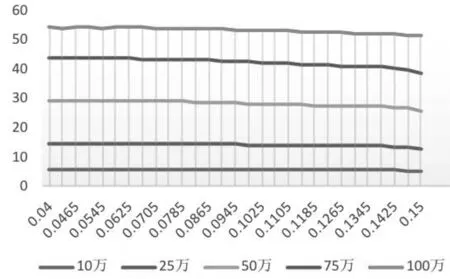
图6 E75企业不同额度利率下的P、Q差值
3 302家无信誉评级的新增中小微企业信贷风险评估及信贷策略决策
3.1 研究思路
在历史企业信贷决策的基础上,首先,采用二项Logistic预测出302家新企业的违约记录,同时考虑到信誉等级并非二值变量,而多分类logistic回归侧重于研究影响因素而非预测,于是采用BP神经网络方法对企业进行信誉等级预测[6].其次,根据基于有效前沿的贷款组合多目标优化决策模型计算出总量为1亿时对302家企业的最优贷款组合投放权重;最终,结合上一步的函数方程式,定量计算出新增企业的具体信贷策略.
3.2 模型的建立与求解
(1)模型的准备
a.基于二项Logistic的违约记录预测
为了对123家企业的数据进行回归拟合,先将上述10个变量全纳入方程,通过SPSS软件进行二分类Logistic回归分析,得到表4,并对初步建立的回归方程根据统计检验P值删除对因变量影响不显著的自变量,显著性水平给定为0.05[7].
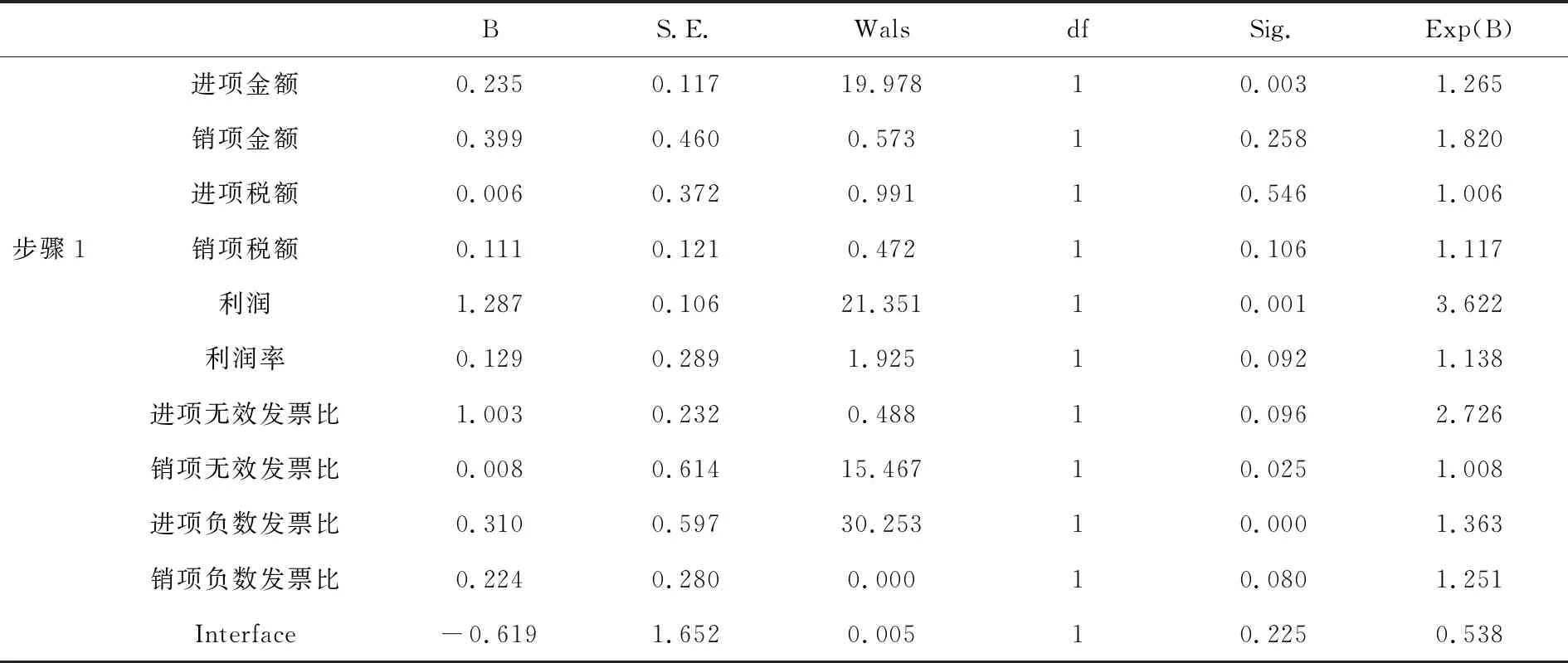
表4 回归方程的自变量统计量表
基于上述分析结果,进一步筛选变量,最终可以得到包括进项金额、利润、销项无效发票比、进项负数发票比4个自变量的Logistic回归方程,相应的分析结果见表5.
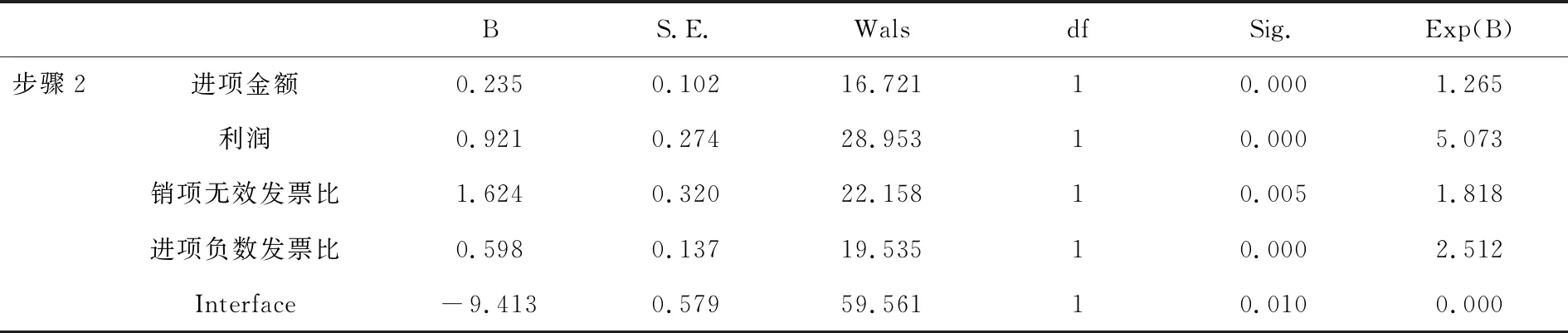
表5 筛选后回归方程的自变量统计量表
从表5中的OR值(即Exp(B)值)可以看出,对“是否违约”影响最大的是销项无效发票比,且影响程度排序为:销项无效发票比>利润>进项负数发票比>进项金额.
最终可以给出回归方程如下:
(7)
利用上文所建立的二元Logistic回归模型,对302家企业的违约记录进行预测,得到初步违约记录结果见表6.

表6 违约记录结果(初步)
b.基于BP神经网络的信誉评级预测
考虑到信誉等级并非二值变量,而多分类logistic回归侧重于研究影响因素而非预测,于是采用BP神经网络方法对企业进行信誉等级预测,其中BP神经网络中的神经元模型如图7所示.首先,将第一部分中的各评价指标为网络输入信息,设置信誉评级为网络目标输出.
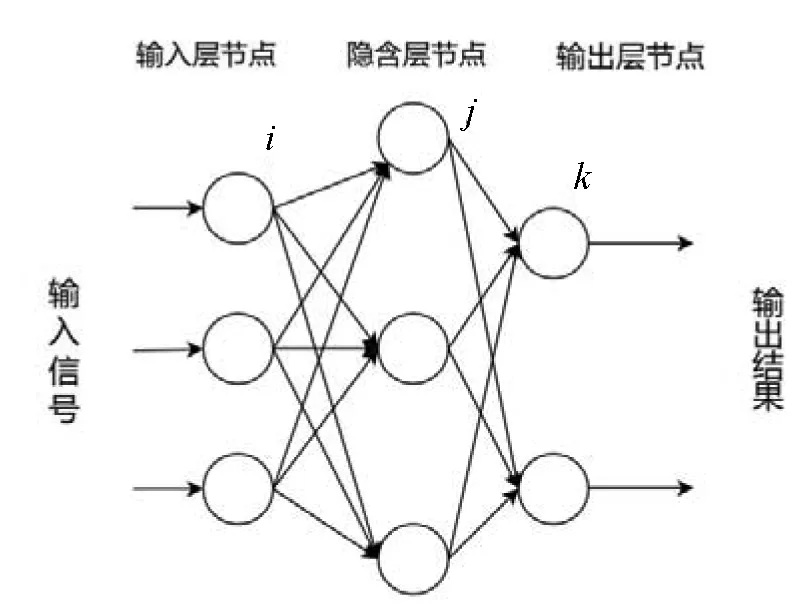
图7 三层BP神经网络结构
其次,将数据归一化在[-1,1]后.建立BP神经网络模型[8],相关参数如下.
除去4个信誉评级数据外的各个研究指标作为输入向量,网络的输入层单元数为10[9].
选择采用Matlab软件保证神经网络中其它参数不变,调整隐含层神经元个数进行重复可控试验,通过对比输出值与期望值之间的误差,确定最佳隐含层神经元个数[9].
从表7可知,在网络经过训练后,隐含层神经元节点数为7时,BP神经网络的均方误差达到最小,最小值为0.0091,此时对函数的逼近效果最好.因此选择隐含层神经元节点的数目为7[10].

表7 网络训练误差
根据以上的分析,所建的BP神经网络的结构为:输入层神经元个数为10;隐含层神经元个数为7,输出层神经元节点数目为1[10].
隐含层神经元之间的传递函数为:对数传递函数,输出层传递函数为:线性传递函数; 网络训练函数为:量化共轭梯度法[10].
网络训练最大迭代次数为:5000; 设置网络学习率:0.05; 设置网络目标学习误差为:5e-5[9].
将123家企业的样本分为两部分,以其中90家企业的样本数据作为训练集训练神经网络,并对剩下的33家企业的样本数据作为验证集进行拟合验证,训练结果如图8所示.
从图8的网络收敛结果可以看出:网络训练95次后收敛,网络误差为1.00e-05,达到了网络误差设置的要求.

图8 神经网络训练结果
从图9的网络整体拟合效果以及图10的拟合优度中可以看出,输出值与实际值重合度较高,网络的拟合优度为0.999以上,拟合优度非常好,即有较好的回归能力.
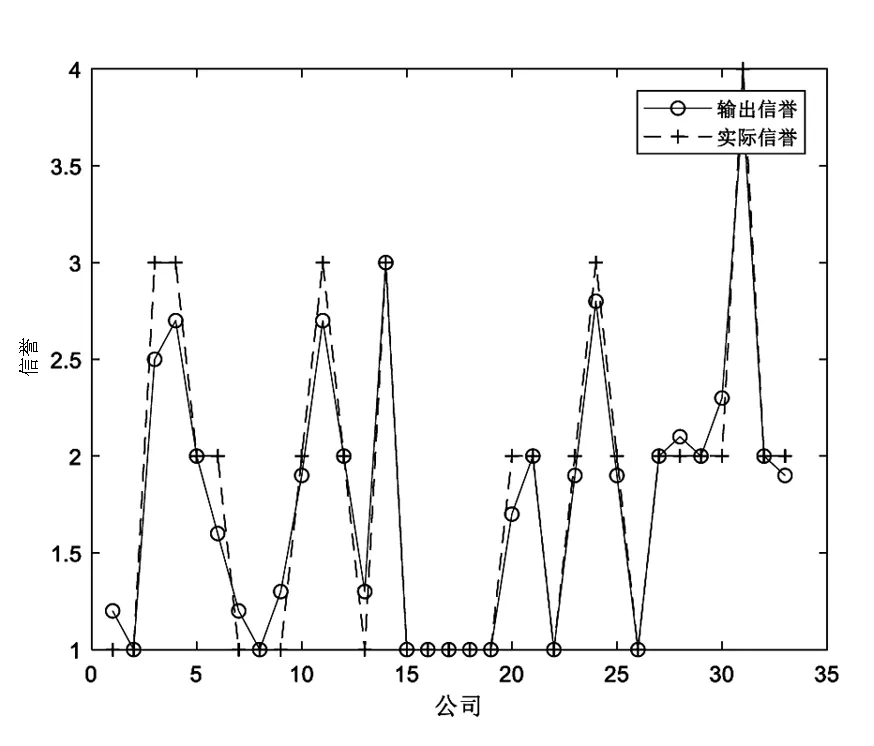
图9 网络训练的误差动态变化图
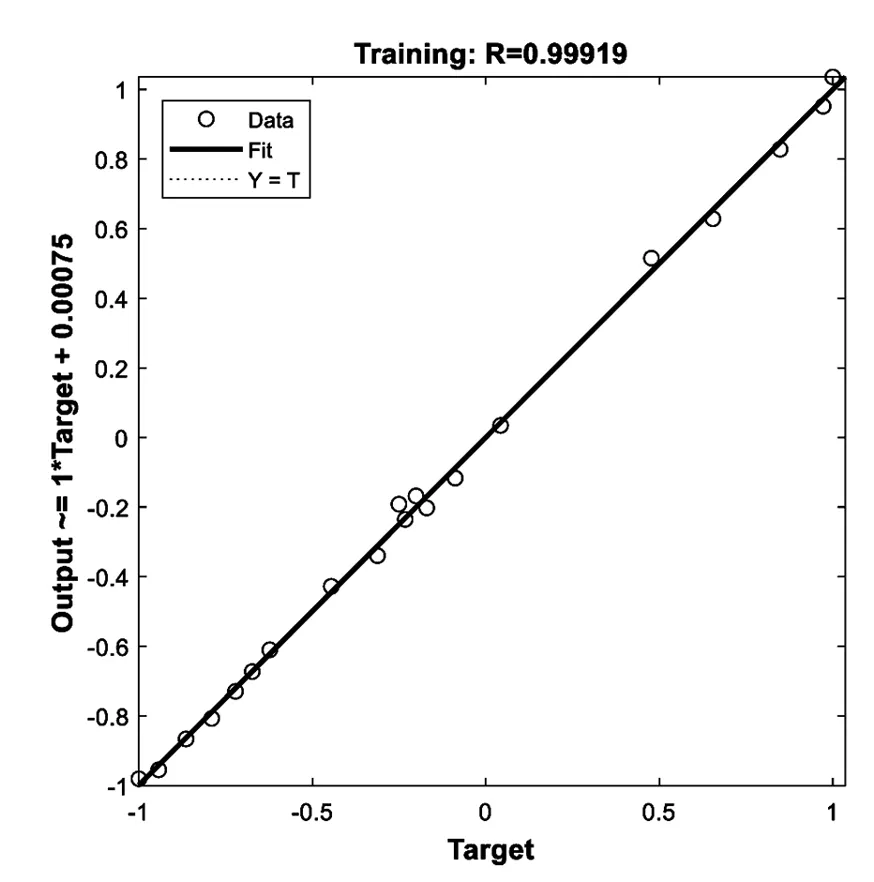
图10 拟合效果及优度
利用上文所建立的BP神经网络模型,对302家企业的信誉评级进行预测,得到初步评级结果见表8.
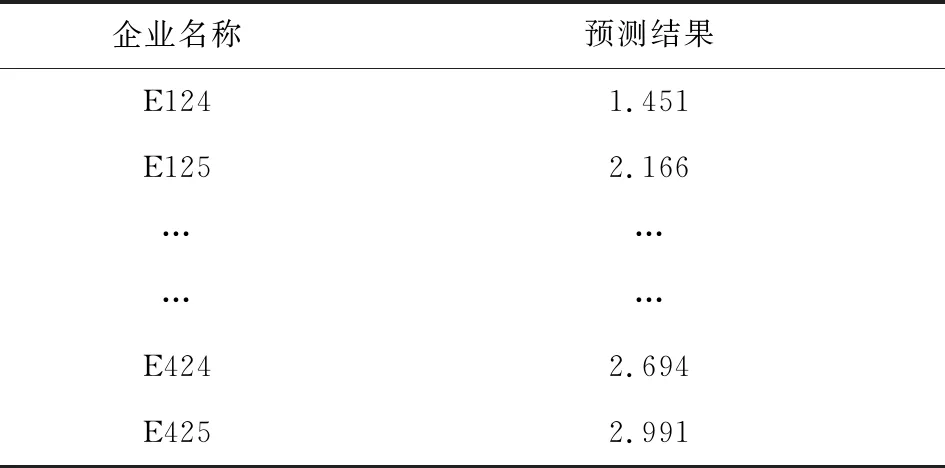
表8 信誉评级结果(初步)
c.预测结果规范化
上文对信誉等级及是否违约的预测结果均为小数,考虑到不同行业的信贷风险不同,以行业分类为依据,把不同行业的违约比例作为一个因素来对信誉等级及是否违约进行考量.
根据国民经济行业分类与代码(GB/4754-2011),对国民经济行业进行见表9分类[11].

表9 行业分类与代码
根据行业分类对123家有信贷记录企业及302家无信贷记录企业进行分类,并对有信贷记录企业的各行业分别统计其违约比例,按照下列规则确定信誉等级及是否违约的最终结果:当信誉等级预测结果在0.66~1.33,1.66~2.33,2.66~3.33,3.66~4.33的范围内时,分别取信誉评级结果为A,B,C,D,当是否违约预测结果在0.66~1时取违约记录为“是”,当是否违约预测结果在0~0.33时取违约记录为“否”;当信誉等级预测结果在1.33~1.66,2.33~2.66,3.33~3.66的范围内、是否违约预测结果在0.33~0.66的范围内时,考虑该企业所属行业的违约比例,若行业违约比例超过50%时,对信誉等级进行降级,即取信誉评级结果为B,C,D,违约记录为“是”,若行业违约比例未超过50%时,对信誉等级进行升级,即取信誉评级结果为A,B,C,违约记录为“否”.据此得到最终结果见表10.
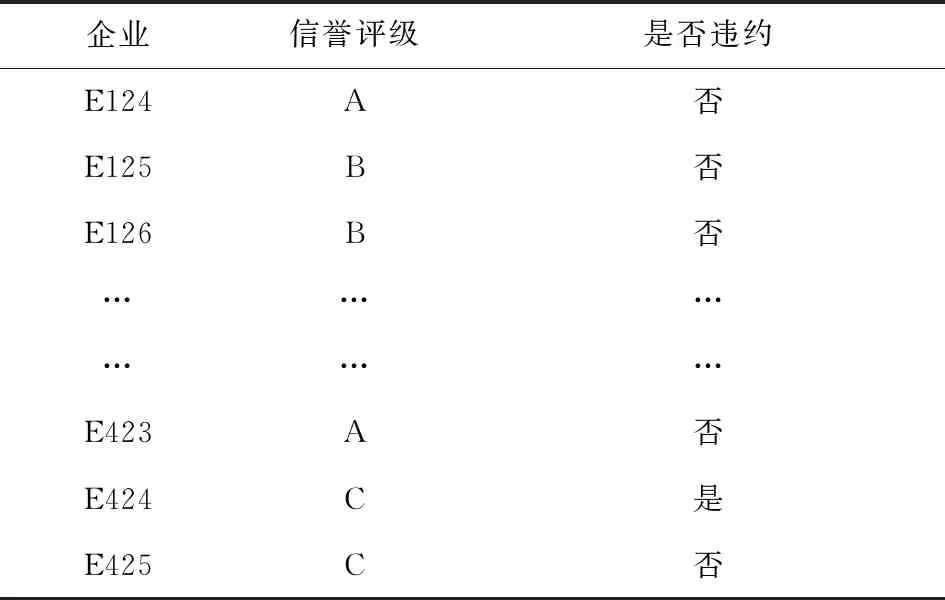
表10 最终结果
(2)模型的建立与求解
求解新增企业的信用水平后,接着利用第一步所建立的指标体系来对这302家企业的信贷风险进行评估.
模型Ⅲ——基于有效前沿的贷款组合多目标优化决策模型
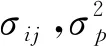
(8)
其中,R=(R1,R2,…,Rn)T为贷款组合中n笔贷款的期望收益率,X=(x1,x2,…,xn)T为贷款组合中n笔贷款的投放权重,B=(σij)n×n是n笔贷款的协方差矩阵[12].
假设302笔不同贷款的投放权重为X=(x1,x2,…,x123)T,计算302家企业的协方差矩阵B并取第一笔贷款的期望收益率为3.7%,其余贷款收益率依次递增,间隔0.01%,代入式(8)中以此构建多目标优化决策模型.
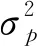
Rp=x1R1+x2R2+…+x301R301+(1-x1-x2-…-x301)R302
(9)
…-x301)σ302,302+2x1x2σ12+…+2x1x301σ1,301+2x1(1-x1-x2-…-x301)σ1,302+…+
2x301,12(1-x1-x2-…-x301)σ301,302
(10)
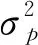
求解出新增企业的信用水平后的信贷风险评估与信贷策略决策与第二部分历史企业的测算思路相同.首先利用PCA-GTD模型对企业信贷风险进行量化,归一化处理得到企业的v值.根据投放权重求得投放额度,由于信贷额度已知,仅需对应变换r和u,以求得放贷企业对应最优利率,继而做出最优组合贷款策略.
以企业E124为例,其信贷投放权重为0.0044,额度为44万元,在该额度下的P、Q差值与r的对应变化如图11所示,可知最优利率为0.665.

图11 E124企业不同利率下的P、Q差值
最终的最优组合策略见表11.

表11 302家企业最优组合策略
4 结束语
信贷风险评估时,将主成分分析与灰靶决策模型有机结合起来,不仅对多维指标进行有效提取与降维,同时结合了灰靶模型在决策中能充分结合主观标准与客观情况的优势进行综合决策,获取最初是否放贷和放贷次序的决策结果,具备了客观计算和评估的目的,量化了中小微企业信贷决策的依据,并形成了标准化的信贷决策流程,这对信贷策略的改进与发展提供了极有利的参考和借鉴;针对可贷款的企业,进一步采用函数关系模型,建立银行收益与风险、利率、贷款额度等之间的函数关系,方法独特,并且能有效计算出相应的信贷策略,有效性实用性强;针对无信誉等级和违约记录的新客户企业时,综合考虑了信誉等级与违约是否的不同,分别采用BP神经网络预测以及回归预测出其信用水平,为下一步信贷风险的评估和信贷策略提供了强有力的支撑.在实际应用中,应当进一步考虑突发事件对不同类别不同行业中小微企业的影响,对以上风险—收益模型做出相应的调整,即分析出突发因素导致的贷款策略调整.

