基于非参数检验对运动员反应时间的相关性分析 *

李 琴，朱家明，郎 红，宋国锋

(安徽财经大学)

0 引言

反应时间是指机体从接受刺激到做出相应反应动作所需的时间，即从刺激到反应之间的时差，主要反应运动员神经与肌肉系统的协调性和快速反应能力[1].起跑反应时间在短距离项目中具有非常重要的地位，它不仅对运动员的心理产生影响，也对起跑后的各阶段技术产生影响，从而影响比赛成绩.世界级的短距离比赛中，运动员的身体素质、运动技巧都相差不大，比赛的胜负通常取决于百分之一秒，运动员的起跑反应就担任了至关重要的作用.通过研究运动员反应时间的相关性分析，能够科学认识运动员反应时间的原理及作用、提供真实可靠的科学依据、启发运动员对“起跑时”训练环节的思考、从而科学合理地安排训练计划，通过科学有效的训练计划手段提高短距离运动员的比赛成绩.Babic等在运动员的起跑反应在性别差异上的研究表明，在2004年奥运会短距离100m男子运动员反应短于女子运动员，且呈显著性差异[2].Martind等研究中也有相似的结论，但同时得出该趋势并不具备统计学意义上的差异[3].Moravec等研究发现此现象无统计学意义上的显著性[4].Giorgos研究发现除个别场次存在显著性差异外，其他并无显著性差异[5].

在不同项目中运动员反应时间的差异研究上，1984年墙壮对不同项目的少年运动员的反应时进行研究，发现各项目中运动员对不同信号刺激的反应时存在显著性差异，在不同项目或相同项目不同技术类型的运动员间，其反应时存在显著性差异[8].张力为等发现在周期性运动项目中，持续时间长短与反应时快慢呈负相关，非周期性项目对反应时要求较高[7,9-10].在不同比赛阶段中运动员反应时间差异研究上，金庆红提出“从预-复-决赛世界优秀短跨运动员的起跑RT呈现缩短的态势的观点[11].董胜利研究发现男运动员各赛次间反应时无显著性差异，女运动员在部分项目赛次间反应速度有显著性差异，男女运动员反应时都呈现前后赛次加快的趋势等一系列研究观点[6].

1 数据来源与假设

该文数据选取了2011～2019年5届世界田径锦标赛短距离跑成绩与运动员起跑反应时的相关数据.为了方便处理问题，提出以下假设：⑴所提供的数据真实可用；⑵关联分析不考虑其他客观因素影响；⑶差异分析在单个因素影响程度研究中忽略其他因素；⑷假设5年及以上起跑反应才构成差异规律；⑸不考虑不同短距离比赛的起跑设施差异.

2 运动成绩与起跑反应时间的关联分析

2.1 研究思路

首先对数据集进行筛选，并进行精确Kolmogorov-Smirnov检验，发现数据集不满足正态分布.结果显示p值过小，不能通过正态性检验，所以采用对原始变量的分布不做要求的相关分析方法.测量起跑反应和运动成绩这两个随机变量相关性，采用适合分类变量对象的非参数假设检验方法kendall秩相关系数法.

2.2 研究方法——关联分析模型及算法

从两变量(xi,yi)(i=1,2,…,n)是否协同一致的角度出发，检验两变量之间是否存相关性.用Nc表示同向数对的数目，Nd表示反向数对的数目，则有公式Nc+Nd=n(n-1)/2.Kendall相关系数统计量由两者的平均差定义如下：

其中:S=Nc-Nd,-1≤τ≤1.

2.3 结果分析

对不同性别、不同项目的6组数据运用R软件进行kendall秩相关分析,见表1.

表1 运动成绩与起跑反应的Kendall系数

根据Kendall秩相关系数法分析可得，男子女子100 m都呈现非常显著性差异，且相关系数较低；男子女子110 m直道、200 m直道和女子100 m跨栏中都呈现显著性差异，且相关系数较低，即为显著低相关.由此可以认为，运动员的运动成绩与起跑反应时有关，并对不同性别和不同项目都存在显著性的差异.且对于比赛项目距离越短的起跑反应时对成绩影响越大.

起跑反应时除与先天素质有关外，还与起跑技术、状态、比赛环境密切相关.对不同项目、不同性别分别进行起跑训练，可以提高反应时的效率，反应时间缩短，并且稳定性提高.

3 差异分析问题的分析与求解

3.1 研究方法——差异分析模型及算法

(1)两独立样本的差异性检验——Mann-WhitneyU检验

记两个独立的连续型随机变量总体X和Y的样本分别为x1,x2,…,xm和y1,y2,…,yn，样本容量为N=m+n.记Wxy为所有X样本和Y样本做比较后Y的样本大于X样本的个数，即

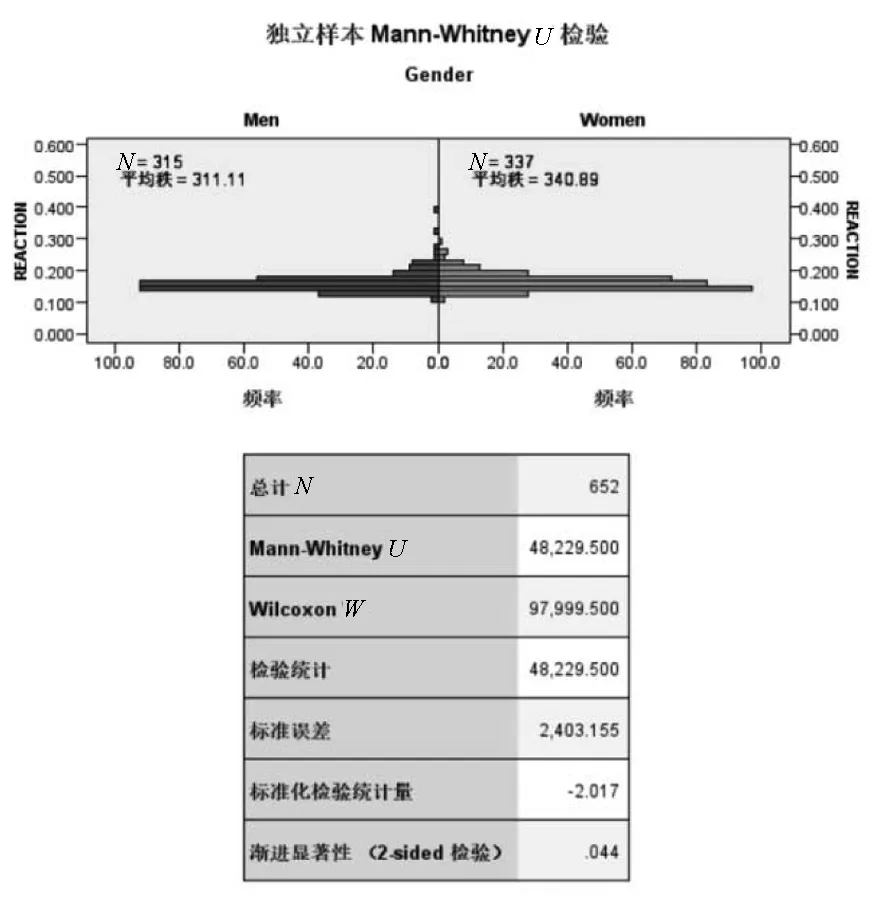
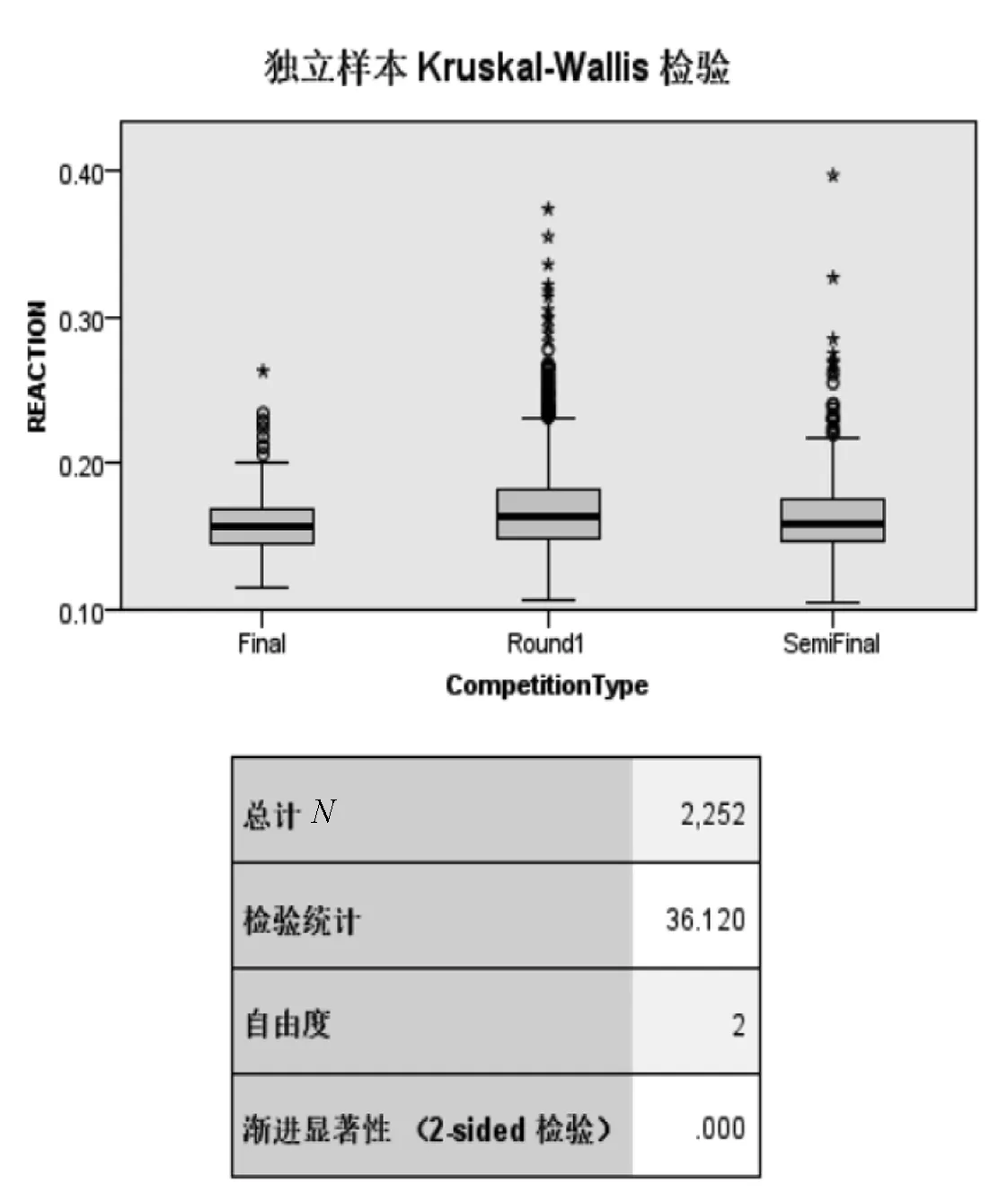
Wxy=#((x,y):xi

则称Wxy为Mann-WhitneyU统计量.同样，Wxy为所有X样本和Y样本做比较后Y的样本小于X样本的个数，即

Wyx=#((x,y):xi>yi,i=1,2,…,m,j=1,2,…,n)

显然有Wxy+Wyx=mn.

(2)多个独立样本的差异性检验——Kruskal-Wallis检验

3.2 研究思路及结果分析

(1)以性别分组的运动员反应时间差异分析

以性别为分组分别对数据集进行筛选，并进行精确Kolmogorov-Smirnov检验，发现数据集不满足正态分布.结果显示p值过小，无法通过正态性检验，选择两独立样本的非参数检验方法Mann-WhitneyU检验.将不同类型的比赛进行细分，分别分为100 m直道，短距离跨栏.通过运行SPSS对运动员反应时间是否有显著的性别差异的问题进行分析，得到结果如图1、2所示(其中0代表女运动员，1代表男运动员).由于p值小于0.05，可认为运动员的反应时间有着显著的性别差异，即男女运动员的反应时间有着显著的差异.

图1 100 m男女运动员反应时间差异检验结果

图2 短距离跨栏男女运动员反应时间差异检验结果

(2)以比赛年份分组的运动员反应时间差异分析

对其不同比赛年份的运动员起跑时的数据集分别进行精确Kolmogorov-Smirnov检验，结果显示p值过小，不能通过正态性检验，选择多独立样本检验的Kruskal-Wallis检验.通过对各届锦标赛数据按照年份分组，运用SPSS对不同项目的3组数据进行Kruskal-Wallis模型检验，分析每1届短距离比赛中起跑反应是否具有差异，结论如图3所示，p值小于0.05，可认为不同年份的短距离比赛中，运动员的起跑反应呈显著性差异.

图3 不同年份中运动员反应时间检验结果

(3)以比赛项目分组的运动员反应时间差异分析

面对独立多样本的检验问题，分别筛选出100、200 m、男子110 m跨栏和女子100 m跨栏不同运动项目的数据，通过精确Kolmogorov-Smirnov检验发现数据集呈非正态分布，选择Kruskal-Wallis检验，分析不同项目中的差异性显著程度.

结果如图4所示，发现运动员在各个运动项目，即100、200 m、男子110 m跨栏和女子100 m跨栏中起跑反应时是存在差异的.从图像中可以清晰的看出，运动员针对不同的运动项目的起跑反应时的侧重程度是不一样的.同时，由p值可知，4种项目中运动员的反应时间差异性呈显著性差异.

图4 不同项目的运动员反应时间检验结果

(4)以比赛的不同阶段分组的运动员反应时间差异分析

在面对比赛不同阶段运动员反应时间的样本，首先通过精确Kolmogorov-Smirnov检验其数据集呈非正态分布.选择通过Kruskal-Wallis模型检验，分析不同项目中间的差异性显著程度.

结果如图5所示，运动员在比赛的不同阶段的反应时间是存在显著差异的，即运动员在初赛、复赛和决赛3个比赛阶段中起跑反应时是存在显著差异的.运动员在第1阶段初赛的起跑反应时的差异是最大的；其次是复赛阶段各运动员的起跑反应时；最后是决赛阶段，各运动员的起跑反应时的差异已经十分接近了.

图5 不同比赛阶段中运动员反应时间检验结果

(5)针对决赛组成员在比赛的不同阶段分组的反应时间差异分析

为保证分析的样本大小，将决赛组成员在不同比赛阶段进行项目分类，即分别分析100 m直道、短距离跨栏中决赛组运动员在初赛、复赛、决赛中反应时间的差异.

首先对数据集进行筛选，并进行精确Kolmogorov-Smirnov检验，发现数据集不满足正态分布.选择Kruskal-Wallis检验，分析决赛组成员在不同项目中反应时间的差异性显著程度.结果如图6、7所示，在100 m直道和短距离跨栏中，运动员的反应时间有着非显著的差异性.

图6 100 m决赛组初复决赛差异检验结果

图7 短距离跨栏决赛组初复决赛差异检验结果

4 结束语

该文善用图表，对数据集进行可视化处理，使得相关性分析简单可见，简洁明了，提供了良好的阅读体验和视觉表现.该文研究发现运动员的起跑反应能力整体都在不断提升，表现为反应时间的逐年下降，5年内总体下降了近0.3 s，有了很大的进步.随着时间的推移、科技的进步、国家对体育比赛的重视以及人们对体育训练的认知更加系统规范科学，使得运动员得到了更加科学有效的训练，使得运动员的反应时间极大的减少，运动员的反应能力得到极大的提高.不同的运动项目接受不同的训练计划，则在一定程度上导致了不同项目中运动员反应时间的差异.预赛到复赛再到决赛，运动员们的起跑反应时差距越来越小，此时运动员的心理素质对比赛成绩就起到一定作用了.