波浪中三体船非线性横摇运动近似解析解及特性分析

张艺瀚，王 平，蔡新功

（中国船舶及海洋工程设计研究院，上海 200011）

0 引 言

三体船型具有较单体船型更好的快速性、耐波性和总布置性等优点[1]，已经在很多实船上得到了体现，包括美国LCS 三体濒海战斗舰、澳大利亚三体高速车客渡船等。实船试验及相关模型试验研究[2]表明，三体船型横摇运动特性与常规单体船型有所不同，在波浪中低速航行时经常发生大幅横摇及不稳定横摇现象，可以通过引入非线性横摇阻尼模型和非线性恢复力模型进行研究。

非线性横摇运动方程从数学角度难以求得精确解析解，通常基于势流理论计算等效线性化阻尼下的稳态运动[3]，此外，利用CFD 可以模拟波浪中的大幅横摇衰减运动[4-5]，但较难精确仿真不稳定的非线性横摇现象，且计算效率较低。为了从理论角度解释三体船可能存在的特殊横摇运动现象，以便在工程中给予指导建议，本文采用非线性动力学理论中的摄动法来定性与定量地分析波浪中非线性横摇运动特性。摄动方法主要有LP 法、多尺度法、平均法[6]等。丁勇等[7]研究了单体船型在静水中的横摇解析解，并通过数值和试验加以验证；胡安康等[8]基于多尺度法研究了集装箱船在横浪中的横摇解析解和横摇特性，但是关于三体船型的近似解析解的相关研究目前还未有学者进行公开报道。三体船型的非线性横摇模型具有一定特殊性，通常其阻尼模型采用线性加平方模型（LPQD）或线性加立方模型（LPCD）[9]，主要根据具体的船型特点和附体型式进行选择[10]。本文研究的某高速三体实船的阻尼模型中，立方阻尼成分明显大于平方成分，在大幅横摇时非线性更加明显，因此本文采用线性加立方的阻尼形式。方程中的非线性恢复力模型可以通过静水力曲线拟合得到，拟合结果也和单体船有所不同，将在后续讨论。

多尺度法对于非稳态运动的适应性较强，并且容易对稳态解作定性分析。本文应用该方法计算得到三体船在波浪中的幅频响应和时历稳态解，并通过模型试验和数值计算进行验证,分析了阻尼系数和恢复力系数对横摇运动特性的影响，从理论角度有效解释了三体船非线性横摇运动的特点和特殊现象，并为三体船的研发设计提供了一定的理论支撑。

1 非线性横摇运动方程及近似解析解

根据线性加立方阻尼模型及后续得到的近似到5 次方的非线性恢复力模型，本文建立的正横浪规则波状态下非线性横摇运动方程如下：

式中，Jφφ、ΔJφφ分别为横摇惯性矩和附加惯性矩，可以根据经验公式[11]或者通过试验获得横摇固有周期，再根据式（2）推导得到。

式（1）中，2Nφφ为线性阻尼系数，N3为立方阻尼系数，C1、C2、C3分别为线性、3 次和5 次恢复力矩系数，可通过稳性力臂曲线拟合得到，其中C1=Dh，D=Δg，h为初稳心高。F为波浪力幅值，可以认为由波浪主干扰力和辐射力叠加而成。其中，波浪主干扰力Ff-k是主要组成部分，通常可以用波倾角表示，Ff-k=Dhae0为波浪力幅值[12]，ae0为有效波面角，考虑船宽和船吃水限制的影响。

为方便后续分析，方程（1）两边同除以Jφφ+ΔJφφ，化简为

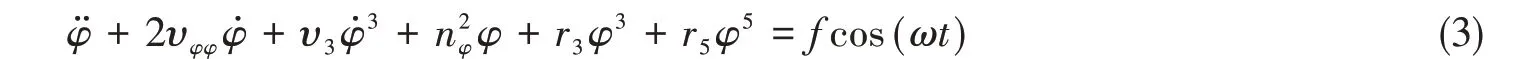
式中，nφ为横摇固有频率，2υφφ为线性横摇阻尼系数，υ3为3次横摇阻尼系数。

20世纪50年代，美国学者Sturrock引入多尺度法[13]，通过引入小参数ε，一系列越来越慢的时间尺度可以表示为

由于本文取到一阶近似解析解，只需取T0=t、T1=εt两项，同时引入激励频率的失调参数δ，使ω=ω0+εδ，其中ω0=nφ，为横摇系统的固有频率。

引入小参数后，将横摇运动方程(3)化为含阻尼的Duffing系统受迫振动标准方程：

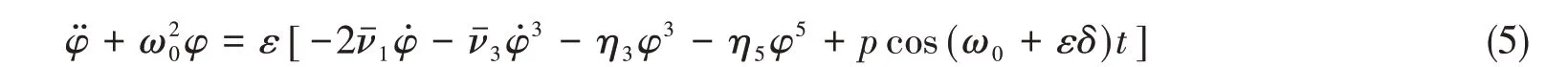
由参考文献[6-8]中的多尺度法摄动推导，得到横摇运动的一阶稳态解为

其中,

横摇幅频响应曲线为

横摇一阶近似解析解为

其中，前两项为一阶近似稳态解

式中，相位γ=δT1-β。

2 三体船算例分析

2.1 计算模型及主要参数

为了验证上述方法对三体船的适用性并分析三体船型非线性横摇特性，采用某三体客船为研究对象，表1为主尺度参数，图1为横剖面图。

图1 三体船横剖面图Fig.1 Cross section of trimaran

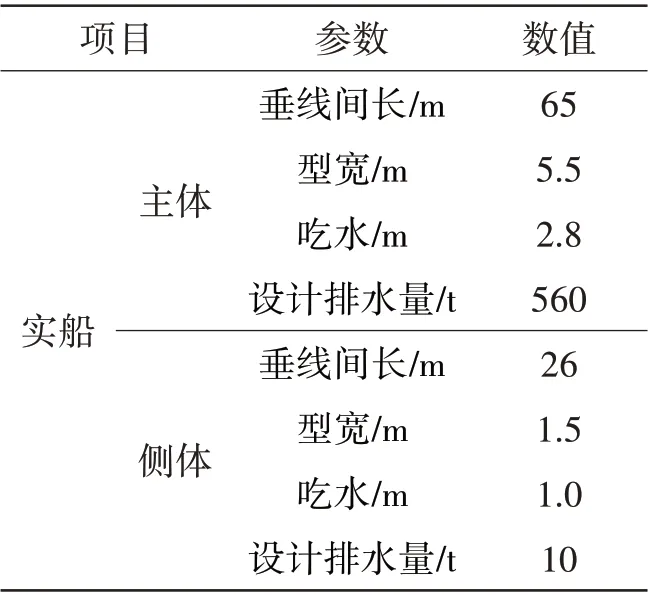
表1 主尺度参数Tab.1 Principal dimensions

计算采用的线性及非线性横摇阻尼系数通过船模横摇衰减试验获取，图2 为船模横摇衰减试验的照片，衰减试验时采用3自由度，即横摇、纵摇和垂荡。图3 为静水横摇衰减曲线，图4 为采用最小二乘法拟合的消灭曲线。可见，对于本文研究三体船型，采用线性加3 次方形式（LPCD）的横摇阻尼模型是合适的。

图2 横摇衰减试验Fig.2 Roll decay experiment

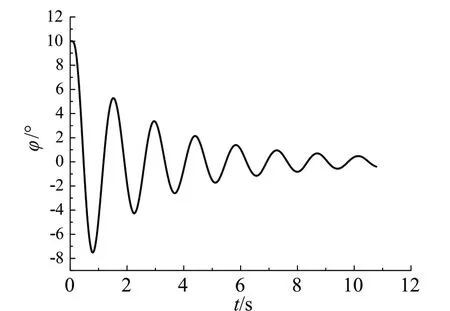
图3 横摇衰减曲线Fig.3 Roll decay curve

图4 横摇衰减消灭曲线Fig.4 Extinction curve of rolling

拟合后的消灭曲线方程为

横摇方程中的非线性恢复力系数通过拟合实船恢复力臂曲线得到。

本船恢复力臂曲线（GZ 曲线）采用NAPA 软件，基于静力学并通过实船自由液面修正后得到，应用最小二乘法得到拟合曲线（见图5），可见拟合程度较高。

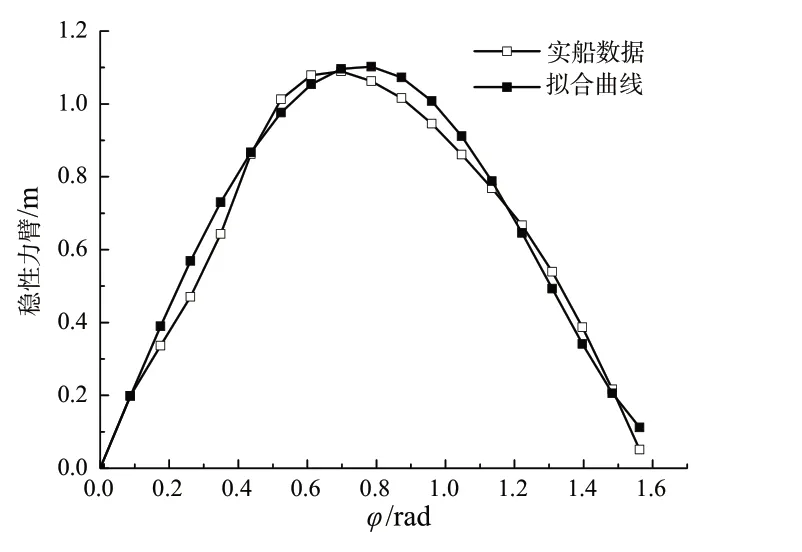
图5 恢复力臂曲线及拟合结果Fig.5 GZ curve and fitting result

非线性恢复力臂拟合方程为

从恢复力臂曲线也可以发现三体船型与单体船的区别，这种船型由于片体的存在，有效船宽较大，导致稳性消失角很大，几乎在90°左右，而单体船通常在60°以下，数值上非线性恢复力系数的正负号与单体船不同，这些因素将使得幅频曲线具有一定的特殊性。

表2为方程中需要用到的具体计算参数，其中需要说明的是附加惯性矩是根据式（2）通过船模试验得到的固有周期反推得到。

表2 计算参数Tab.2 Parameters for calculation

2.2 数值及试验验证

2.2.1 试验验证取单位波幅横浪规则波，将实船参数代入式（8），得到横摇幅频曲线，如图6所示。实船阻尼下，在波浪激励频率与横摇固有频率比接近1时，横摇幅值达到最大值，对应横摇非线性系统发生主共振的情况。随着阻尼的减小，主共振的幅值会沿着骨架线逐渐增大，幅值对应的频率向右侧倾斜，表现出刚性软化的趋势，但随着阻尼的进一步减少，又展现出刚性渐硬的趋势，直到极限情况下的无阻尼状态，系统的幅值可能达到最大值，成为所有阻尼情况下的包络线。为了验证幅频曲线的正确性，针对该三体船开展了横摇规则波试验，本试验在哈尔滨工程大学拖曳水池开展，如图7所示，通过三自由度适航仪进行零航速横摇运动试验，系列规则波取多个不同的周期，比如（0.5～2.0 s），分别造出波高约为0.05 m 的规则波，记录横摇角的时间序列，并进行时域统计得到幅频响应曲线，图8为横浪规则波试验照片。幅频曲线与试验值的对比见图6。从图中可见，应用近似解析法得到的实船幅频曲线与试验值吻合良好，平均误差在10%以内。

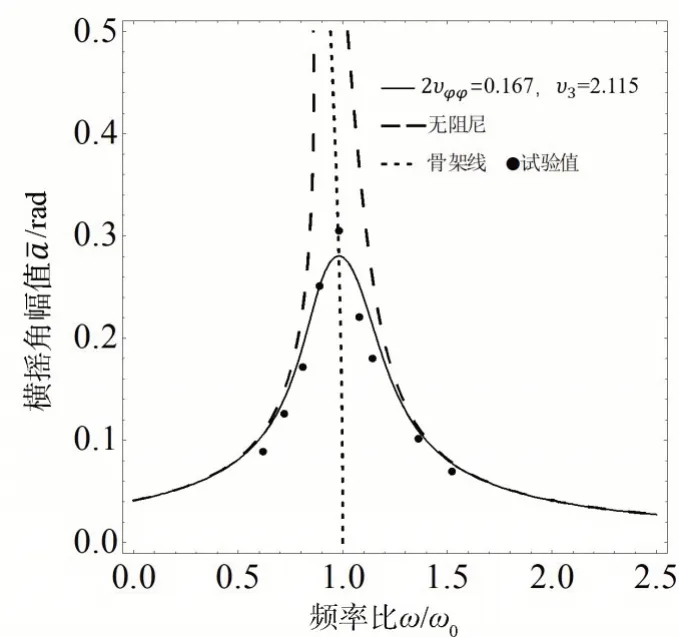
图6 横摇幅频响应曲线Fig.6 Amplitude-frequency response curves of rolling

图7 拖曳水池Fig.7 Towing tank

图8 横浪规则波试验Fig.8 Rolling test in regular beam waves

2.2.2 数值验证

针对式（1）表达的非线性横摇方程，应用4 阶龙格库塔法直接进行数值求解[14]，取ω/ω0= 1 的情形，初始横摇角取为3°。同时，在结果中加入了对应波浪频率下试验稳态值的对比，其中图9 为数值解法与多尺度法的对比，可见数值解法可以展现横摇运动从初始到稳定的过程，多尺度法与数值解较为接近。图10 为多尺度法近似解析解的稳态值与试验稳态值的对比，周期吻合度较高，幅值误差约为8%。

图9 多尺度法与数值解的比较Fig.9 Comparison of multi-scale method and numerical solution

图10 多尺度法与试验值的比较Fig.10 Comparison of multi-scale method and experimental values

2.3 横摇运动特性分析

三体船横摇运动的非线性成分主要体现在阻尼非线性和恢复力非线性。本文通过基于多尺度法得到的幅频曲线研究这两种非线性因素对横摇运动的影响，进而分析三体船型的横摇运动特性。

2.3.1 阻尼系数的影响

本文研究的三体船横摇非线性阻尼模型为线性加三次阻尼模型，分别按同比例缩减的原则改变线性阻尼和非线性阻尼的大小得到幅频曲线，如图11 所示。横摇阻尼的存在使横摇运动保持稳定，其大小的变化主要体现在横摇幅值的大小上，并不会改变曲线形状和运动稳定性，无论是线性阻尼的变化还是非线性阻尼的变化，都不会改变幅频响应曲线的框架，随着阻尼的减小，都向着无阻尼情况的趋势在发展，非线性阻尼系数的变化对于幅值变化更加敏感。另外，随着阻尼系数的减少，横摇系统除了幅值增加外，还会出现多值、跳跃等现象。由于三体船的非线性横摇阻尼在总阻尼中占的成分较单体船更大，因此在三体船的设计中，提供较大的非线性阻尼成分对三体船型的横摇运动控制起着关键作用，例如通过增加减摇水翼、舭龙骨等附体，可以提供一定的非线性漩涡阻尼，对横摇运动具有较大的改善作用。另外，对比文献[15]中单体船情况，三体船在大阻尼下幅频曲线变化规律与单体船基本一致，但随着阻尼的减少，三体船的最大幅值提升更快，从非线性动力学角度来看，由大阻尼状态下的刚度软化变成刚度硬化的趋势，更容易出现大幅横摇和不稳定的运动状态。因次，保证三体船的横摇阻尼是保证其横摇运动稳定性的关键。

图11 阻尼对横摇的影响Fig.11 Effect of damping on rolling

2.3.2 恢复力的影响

包括单体船、双体船或三体船在内的不同船型的恢复力臂曲线都有各自的特点，通常应用高阶模型拟合非线性恢复力。针对三体船，从上述研究中发现恢复力臂拟合到5阶非线性项较为合适，线性及高阶恢复力系数分别为C1、C3、C5，从研究横摇非线性派生系统的稳定性角度，这些系数的大小和正负能够影响横摇幅频响应曲线的形状。

（1）恢复力系数正负的影响

线性恢复力系数C1＞0，其大小由初稳心高决定。三次项系数C3主要调整恢复力臂曲线的形状，船舶的恢复力力臂随着横倾角的增加都是先增加后减少为零（对应的为稳性消失角），导致系数C3＜0。而五次项系数C5主要与稳性消失角的大小有关，随着稳性消失角增加，其符号呈现由负到正的变化趋势。本文研究的三体船由于稳性消失角较大，C5＞0，而单体船稳性消失角较小，往往为负值。这也可以从三体船船型的布置特点进行理解，随着三体船片体从最靠近主体的位置往外侧移动，相当于由单体船变成三体船，恢复力变大，稳性消失角变大。因此，C5会随着三体船的布局变化正负，同时也和重心的位置有关。图12为不同C5下的横摇幅频响应曲线，可见，当C5＞0时，幅频曲线表现出刚度渐硬的趋势，在小阻尼时有发生大幅不稳定横摇的可能性；当C5＜0 时，幅频曲线表现出刚度渐软的趋势，在小阻尼时横摇幅值趋于固定值，不容易发生横摇不稳定现象。

图12 横摇幅频曲线Fig.12 Amplitude-frequency curves of rolling

（2）恢复力系数大小的影响

三体船的船型特点决定了其稳性消失角较大，导致C5＞0。图13 为不同大小的五次方恢复力系数C5对幅频曲线的影响。可见，在偏离主共振频率段和大阻尼情况下，横摇幅值在不同恢复力大小下基本吻合，但在小阻尼主共振及附近频率段，曲线形状随着C5的减小有由刚度渐硬向渐软转变的趋势，发生不稳定横摇的横摇幅值有逐渐变小和稳定的趋势。因此，三体船设计时，在不能控制阻尼的情况下，可以通过改变船型布局及重心高度的方式控制恢复力系数来减少不稳定大幅横摇发生的概率。

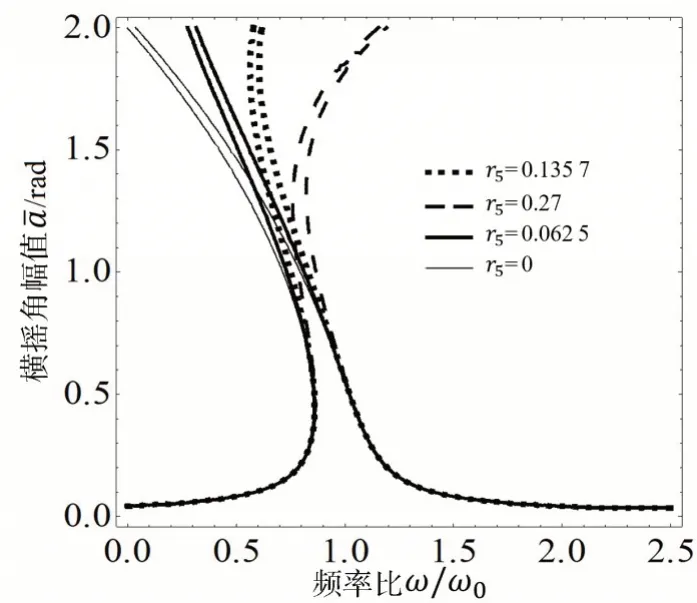
图13 恢复力系数C5(r5)的大小对横摇的影响Fig.13 Effect of the amplitude of C5(r5)on rolling

3 结 论

（1）多尺度法近似解析解适用于三体船非线性横摇运动的求解，可以用来定性和定量分析三体船型的横摇非线性运动特性。由三体船的船型特点决定的非线性横摇阻尼和非线性恢复力系数形式会使其在小阻尼情况下有发生大幅横摇的可能性。

（2）三体船横摇阻尼系数的成分中非线性横摇阻尼系数占较大成分，对三体船在波浪中保持稳定的横摇运动起到关键作用。在设计研发时，采取增加非线性横摇阻尼的措施有利于提升横摇运动性能。

（3）三体船恢复力系数大小和正负会影响主共振附近区域的横摇幅值变化趋势，可以通过改变船型布局及参数控制来减少不稳定大幅横摇发生的概率。