双边箱钢主梁剪力滞效应分析

武芳文,周静雯,赵洋洋,王广倩

(长安大学 公路学院，陕西 西安 710064)

0 引言

随着技术的革新和新材料的出现，薄壁箱梁从其强度、刚度、经济性以及降低自重等方面来考虑是一种合理且有效的结构形式，双边箱主梁便是由薄壁箱梁延伸出的一种截面形式[1]，其具体构造通过实际工程的运用而日渐发展并适应新型结构，然而对于较宽的钢桥面板往往会出现明显的剪力滞效应。通常，由于狭窄翼缘的剪切扭转变形不大，其受力性能接近于简单梁理论的假定；而宽翼缘因为剪切扭转变形较大，不可忽略不计，使得远离腹板处的翼缘不参与承弯工作，这种现象就称为“剪力滞后效应”。当顶板与腹板交界处纵向正应力大于初等梁理论的值时，称为“正剪力滞”现象；反之，则称为“负剪力滞”现象[2]。

目前国内外学者采用理论分析、数值模拟和试验研究3种方法对箱梁的剪力滞效应进行了分析。Lertsima等学者根据有限元模型对影响简支梁和连续梁剪力滞效应的参数进行研究，同时通过模型实验研究，提出了在承受不同荷载时剪力滞系数和竖向位移的函数关系式[3-5]，与规范相比，其计算结果偏大。Mathee等人考虑了钢-混凝土组合梁中混凝土桥面板的正应力沿厚度方向变化的特点，提出了一种确定组合截面有效翼缘宽度的计算方法[6]，但仅对于简支边界下弹性范围内的力学行为进行了研究。Macorini等人考虑了钢-混凝土连接处的变形及混凝土板剪力滞效应的影响，提出了一种适合钢-混凝土组合梁长期分析的有限元模型[7]，但需要进一步进行实验和参数研究，来确定混凝土的收缩徐变和张拉开裂对组合梁有效分布宽度的影响。李夏元等人考虑了各翼板翘曲位移函数幅值之间的关系，基于Timoshenko梁理论对单箱单室薄壁箱梁的剪力滞效应进行了研究[8]，但剪切变形对挠曲变形的影响程度，仍有待进一步进行分析研究。S.M.Chen等人基于有限元法对体外预应力钢-混凝土组合梁的有限宽度传统表达式进行了参数化分析[9]。S.J.Zhou建立了考虑弯矩和剪切滞后变形相互作用的有限元方法，应用所提出的公式分析了在均布荷载和集中荷载作用下，剪力滞对简支箱梁和连续箱梁的挠度、内力和剪力滞系数的影响[10]，但所提出的方法主要适用于单箱单室箱梁。Y.Ma等提出了一种新的空间网格模型来考虑剪力滞效应，分析了边跨和中跨关键截面上的横、纵向剪力滞系数分布规律[11]。尽管目前各国学者所进行的研究工作已有部分成果纳入规范中[12-15]，但已有对箱梁剪力滞的研究并不一定适用于此类双边箱结构，且无论从既有研究文献还是工程技术标准来看，对于双边箱钢主梁的剪力滞问题和可能带来的不利影响，国内外设计规范目前没有统一规定。

本文结合已有研究成果，运用有限元法分析了宽跨比对剪力滞系数变化规律的影响，利用典型边界条件下该类箱梁的剪力滞效应特点，提出用于计算双边箱钢主梁的有效分布宽度系数计算公式，根据公路新桥规计算的结果得到修正系数，为研究双边箱钢主梁的剪力滞效应及相应规范的完善积累基础性技术资料。

1 有限元模型建立

双边箱钢主梁是由顶板、底板、腹板及U形加劲肋等各种加劲构造组成。主梁横断面设计参数如下：桥面宽度为48.5 m；截面高度为3.5 m；钢桥面板厚度为16 mm，设有U形加劲肋；顶板、底板及腹板厚度均为16 mm，设有板式加劲肋。双边箱钢主梁的横断面图如图1所示。

图1 双边箱钢主梁横断面图(单位：mm)

本文基于通用有限元软件ANSYS建立双边箱钢主梁模型，加劲梁和U肋均采用SHELL63单元进行建立，主梁采用Q345钢，弹性模量取值E为2.06×106MPa，泊松比取值μ为0.3，有限元模型如图2所示。

图2 空间板壳模型

选取工程中常用静定体系的边界条件，分为如下4个计算工况：①均布荷载q=10 kN/m；②边界条件：简支梁、悬臂梁；③均布荷载作用位置：双边箱的腹板顶部，荷载的横向分布如图3所示；④主梁宽跨比η=B/L定义为主梁的桥面宽度与跨径之比，其值取0.5、0.3、0.25、0.2、0.17、0.14、0.13、0.11、0.10。

图3 均布荷载作用位置图

计算上述工况下边箱梁悬臂外端、边箱梁腹板顶部、边箱梁顶板中心、主梁截面中心线处顶板、边箱梁腹板底部和边箱梁底板中心这6个计算位置的剪力滞系数，6个位置依次对应图4中1、2、3、4、5、6号节点。

图4 剪力滞系数计算点

2 宽跨比对双边箱钢主梁剪力滞效应的影响

为了控制其他参数影响，保持其他参数为基准尺寸且不变动，分别采用9种宽跨比η(分别取0.5、0.3、0.25、0.2、0.17、0.14、0.13、0.11、0.10)的双边箱钢主梁截面，研究简支和悬臂边界条件下双边箱主梁剪力滞系数的变化规律。

2.1 宽跨比对双边箱简支梁剪力滞效应的影响

当边箱梁腹板顶部承受均布荷载时，双边箱简支梁6个控制部位的剪力滞系数随宽跨比的变化关系如图5、图6所示。

图5 不同宽跨比下的简支梁跨中顶板剪力滞系数

图6 不同宽跨比下的简支梁跨中底板剪力滞系数

由图5和图6可知：当边箱梁腹板顶部承受均布荷载作用时，宽跨比对双边箱简支梁的剪力滞系数影响十分显著，当宽跨比由0.5减小至0.1时，6个计算位置的剪力滞系数逐渐接近于1，剪力滞系数的最大值位于边箱腹板顶部，其值由1.305减小为1.019，变化幅度约为21.9%。当主梁宽跨比减小时，双边箱简支梁的剪力滞效应逐渐减小，截面的正应力分布趋于均匀。

2.2 宽跨比对双边箱悬臂梁剪力滞效应的影响

当边箱梁腹板顶部承受均布荷载作用时，双边箱悬臂梁6个控制部位的剪力滞系数随宽跨比的变化关系如图7、图8所示。

图7 不同宽跨比下的悬臂梁跨中顶板剪力滞系数

图8 不同宽跨比下的悬臂梁跨中底板剪力滞系数

由图7和图8可知：当边箱梁腹板顶部承受均布荷载作用时，宽跨比对双边箱悬臂梁的剪力滞系数影响十分显著，当宽跨比由0.5减小至0.1时，6个计算位置的剪力滞系数逐渐接近于1，剪力滞系数最大值位于边箱腹板顶部，其值由1.189减小为1.002，变化幅度约为15.7%。当主梁宽跨比减小时，双边箱悬臂梁的剪力滞效应逐渐减小，截面的正应力分布趋于均匀。

3 有效分布宽度系数

3.1 有效分布宽度定义

有效分布宽度，指当初等梁理论公式计算的应力值与实际应力峰值近似相等时，其翼缘板实际宽度的折算值；其几何解释为：如图9中所示的实际应力曲线所包围的面积和实际应力峰值与有效分布宽度的乘积相等。

图9 箱梁翼缘板有效分布宽度示意图

翼缘板有效分布宽度计算如式(1)所示[16]：

(1)

其中,bc为翼缘的有效分布宽度；b为翼缘的实际宽度；y为沿横桥向的坐标。

3.2 有效分布宽度系数定义

由于国内外规范尚未对双边箱主梁的有效分布宽度进行规定，故引入参数 “有效分布宽度系数”的概念，该参数定义为：翼缘板有效分布宽度和实际宽度之比，其计算表达式为：

(2)

其中，ρ为有效分布宽度系数；bc为翼缘板的有效分布宽度；b为翼缘板的实际宽度。

将式(2)代入式(1)中，可求得：

(3)

由式(3)可知有效分布宽度系数与截面的最大剪力滞系数成倒数关系。

3.3 宽跨比对有效分布宽度系数的影响

根据式(3)，求出在不同宽跨比和边界条件下的双边箱钢主梁有效分布宽度系数，计算结果如表1所示。

表1 双边箱跨中截面的有效分布宽度系数Table1 Effectivewidthcoefficientofthemid-spansectionofthedouble-sidedboxgirder宽跨比η简支梁悬臂梁顶板底板顶板底板0.50.7661.6890.8411.0370.30.8951.5720.9201.0160.250.9351.4080.9561.0110.20.9461.3730.9751.0110.170.9591.3490.9861.0090.140.9661.1720.9921.0090.130.9741.0440.9971.0090.110.9791.0290.9981.0080.10.9811.0160.9981.008

4 实用计算公式

4.1 双边箱钢主梁有效分布宽度系数的计算公式

剪力滞效应可以用有效分布宽度来表达，现如今许多国家都以有效分布宽度的方式来表达剪力滞效应的影响，将其写入到设计规范中，并给出了计算公式[17]。

根据表1计算所得的数据，并通过Matlab对双边箱简支梁和双边箱悬臂梁在均布荷载作用下，跨中截面的有效分布宽度系数ρ进行了数值模拟推导，可按照4次曲线进行拟合，即：

(4)

式中：A1i～A5i为宽跨比的影响系数。

根据最小二乘法多项式曲线拟合即可得到A1i～A5i如表2所示，相应的回归分析函数如图10所示。

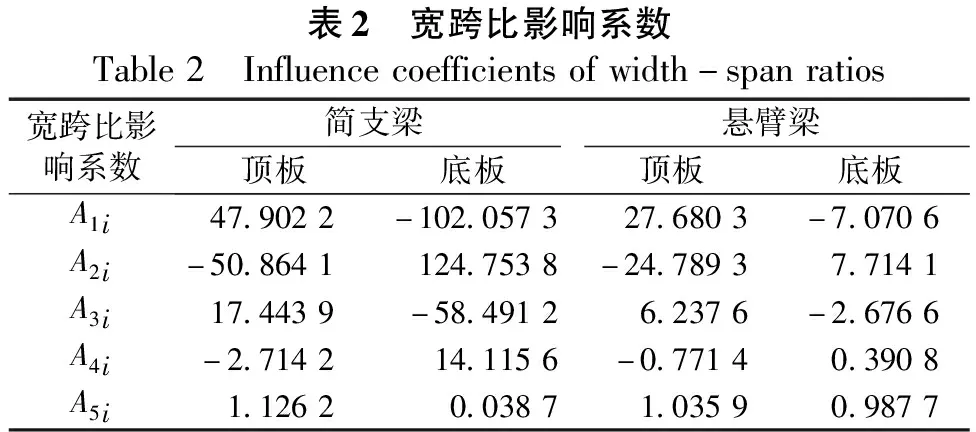
表2 宽跨比影响系数Table2 Influencecoefficientsofwidth-spanratios宽跨比影响系数简支梁悬臂梁顶板底板顶板底板A1i47.9022-102.057327.6803-7.0706A2i-50.8641124.7538-24.78937.7141A3i17.4439-58.49126.2376-2.6766A4i-2.714214.1156-0.77140.3908A5i1.12620.03871.03590.9877

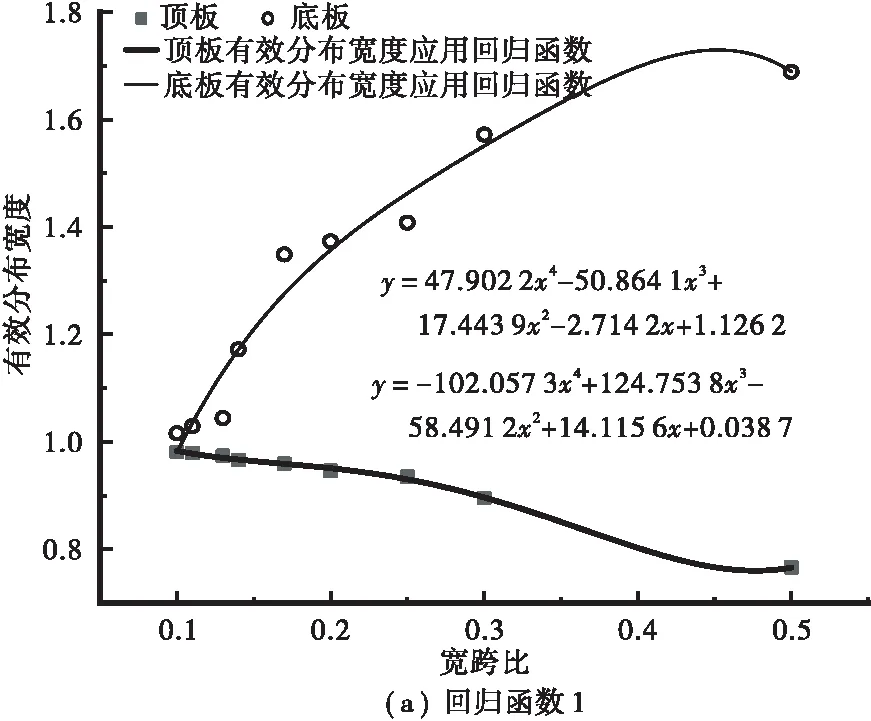
图10 双边箱钢主梁有效分布宽度系数回归函数

分别把表2中的宽跨比影响系数代入式(4)中，取宽跨比η= 0.5、0.3、0.25、0.2、0.17、0.14、0.13、0.11、0.1进行计算，即得到双边箱简支梁和双边箱悬臂梁在均布荷载作用下的顶、底板有效分布宽度系数，将实用计算公式得到的计算结果与有限元分析的数据进行对比分析，得到如表3所示的双边箱有效分布宽度系数的相对误差值。

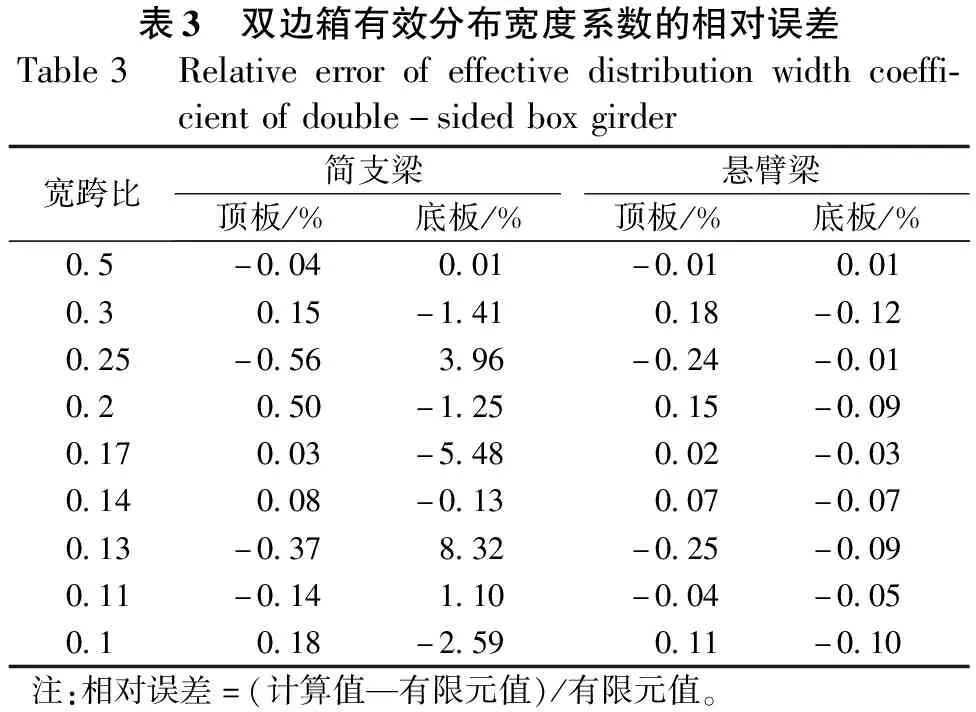
表3 双边箱有效分布宽度系数的相对误差Table3 Relativeerrorofeffectivedistributionwidthcoeffi-cientofdouble-sidedboxgirder宽跨比简支梁悬臂梁顶板/%底板/%顶板/%底板/%0.5-0.040.01-0.010.010.30.15-1.410.18-0.120.25-0.563.96-0.24-0.010.20.50-1.250.15-0.090.170.03-5.480.02-0.030.140.08-0.130.07-0.070.13-0.378.32-0.25-0.090.11-0.141.10-0.04-0.050.10.18-2.590.11-0.10注:相对误差=(计算值—有限元值)/有限元值。

由表3可知，双边箱有效分布宽度系数的相对误差绝对平均值小于1%，说明拟合公式计算精度良好，满足工程计算的精度要求。

4.2 本文计算公式与规范公式的对比

参考《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG3362-2018)》4.3.4中对单箱单室箱梁有效分布宽度的规定，计算双边箱主梁的有效分布宽度系数，与根据实用计算公式计算得到的数据进行对比，并给出相应的修正系数(如表4和表5所示)。

表4 双边箱简支梁有效分布宽度系数修正Table4 Modificationofeffectivedistributionwidthcoefficientofsimplysupporteddouble-sidedboxgirder宽跨比有效分布宽度系数本文规范修正0.50.7660.9380.8170.30.8970.9890.9070.250.9301.0130.9180.20.9501.0270.9180.170.9591.0370.9250.140.9671.0430.9270.130.9701.0480.9260.110.9781.0520.9300.10.9831.0550.932

根据表4和表5可知，一般情况下，若要通过《公路钢筋混凝土及预应力混凝土桥涵设计规范 JTG3362-2018》中条文4.3.4的规定计算双边箱简支梁的有效分布宽度，其有效分布宽度系数的修正值可以取0.911；计算双边箱悬臂梁的有效分布宽度时，有效分布宽度系数的修正值可以取0.923。

表5 双边箱悬臂梁有效分布宽度系数修正Table5 Modificationofeffectivedistributionwidthcoefficientofcantileverdouble-sidedboxgirder宽跨比有效分布宽度系数本文规范修正0.50.8410.9890.8500.30.9211.0210.9020.250.9541.0370.9200.20.9771.0460.9340.170.9861.0520.9370.140.9931.0560.9400.130.9941.0590.9390.110.9981.0610.9410.10.9991.0630.940

5 结论

本文采用有限元法对双边箱钢主梁在简支和悬臂两种边界条件下的剪力滞效应进行了计算分析，得出了考虑不同宽跨比的双边箱钢主梁剪力滞系数分布规律，同时拟合出以宽跨比为自变量的有效分布宽度系数计算公式，主要结论如下：

a.当双边箱钢箱梁承受均布荷载作用时，简支梁跨中断面处的剪力滞系数最大值位于边箱腹板顶部，悬臂梁跨中断面处的剪力滞系数最大值位于桥面中心处。

b.宽跨比η在取0.25～0.5时，主梁的剪力滞效应变化幅度最大；当η小于0.25时，剪力滞效应较小；且随着η的减小，主梁剪力滞效应的变化幅度越来越微弱，截面应力分布愈加均匀。

c.与《公路钢筋混凝土及预应力混凝土桥涵设计规范 JTG3362-2018》对箱梁有效分布宽度的规定对比可知，应用回归分析法提出的实用计算公式能满足工程计算精度要求。