自锚式悬索桥拉-吊体系转换主缆位移特性分析

吴海军，何 立，郭 辉，王邵锐，王 桢

(1.重庆交通大学，重庆 400074； 2.省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074; 3.铁科院(北京)工程咨询有限公司，北京 100081)

自锚式悬索桥造型美观、结构新颖，景观及造型上的优势使这种桥型发展迅速[1-3]。自锚式悬索桥传统施工法通常需要搭设支架或临时墩实现主梁安装及体系转换，对施工现场的地形条件有较高要求，这限制了自锚式悬索桥的发展[4-6]，而“先斜拉，后悬索”(即先采用斜拉扣挂法安装主梁，形成临时斜拉桥；再架设主缆、张拉吊索，形成“斜拉-悬索”共存体系；最后拆除斜拉索，形成悬索桥)施工法能有效解决此难题，该方法在2019年即将建成的鹅公岩轨道专用桥中得到首次应用。鹅公岩轨道专用桥是主跨为600 m的自锚式悬索桥，即将超越当前已建成的主跨为480 m的世界最大跨径自锚式悬索桥——爱沙尼亚穆胡岛桥而成为新的世界之最。鹅公岩轨道专用桥主跨为长江主航道，为了确保长江正常通航，防止船只撞上桥梁支架，鹅公岩轨道专用桥不能在长江航道里搭建支架或顶推成梁，因而首次采用“先斜拉，后悬索”的总体施工方案，运用斜拉扣挂施工法实现体系转换，施工方法新颖、独特，体系转换技术难度高，转换过程中，结构受力、变形过程复杂，国内外工程界尚无成熟经验可以直接应用，相关研究也极少。

目前，针对大跨径自锚式悬索桥主缆位移特性已有部分学者进行了相关研究，如檀永刚[7]等提出自锚式悬索桥主缆弱相干性原理，并通过金华康济桥进行了实桥论证；张俊平[8]等通过模型试验研究了猎德大桥主缆位移在体系转换过程中的演变规律，并明确指出了主缆弱相干性特性的适用条件；王桢[9]等采用模型试验与数值模拟相结合的方法分析了桃花峪黄河大桥主缆随施工阶段的变化规律，对主缆弱相干性适用条件进行了探讨。但以往的研究均是基于传统的体系转换方式，而工程界对“先斜拉，后悬索”体系转换过程中主缆位移变化规律及几何非线性行为表现等认识不够深入和全面，特别是当主跨跨径从400 m级突破至600 m级时，其结构体系力学特性将发生质的变化，且随着跨径不断增大，其几何非线性亦更加突出。有鉴于此，本文以鹅公岩轨道专用桥为依托，研究大跨自锚式悬索桥在“先斜拉，后悬索”体系转换过程中主缆的位移变化规律，以期为同类型桥梁的建设提供参考。

1 工程概况

鹅公岩轨道专用桥主桥跨径布置为(50+210+600+210+50)m，为双塔五跨自锚式悬索桥，桥跨布置如图1。主梁为钢-混混合梁，主缆锚固段及锚跨段采用预应力混凝土结构，混凝土箱梁与钢箱梁之间设钢-混结合段，边跨钢箱梁采用顶推法施工，中跨钢箱梁采用斜拉扣挂悬臂拼装施工法，钢箱梁标准节段梁长15 m。主缆矢跨比为1/10，主缆采用高强平行钢丝束，标准强度为1 860 MPa，缆间距为19.5 m;吊杆采用高强平行钢丝束，标准强度为1 770 MPa，吊杆间距为15 m。两岸主塔高度一致，均为钢筋混凝土门形构造。

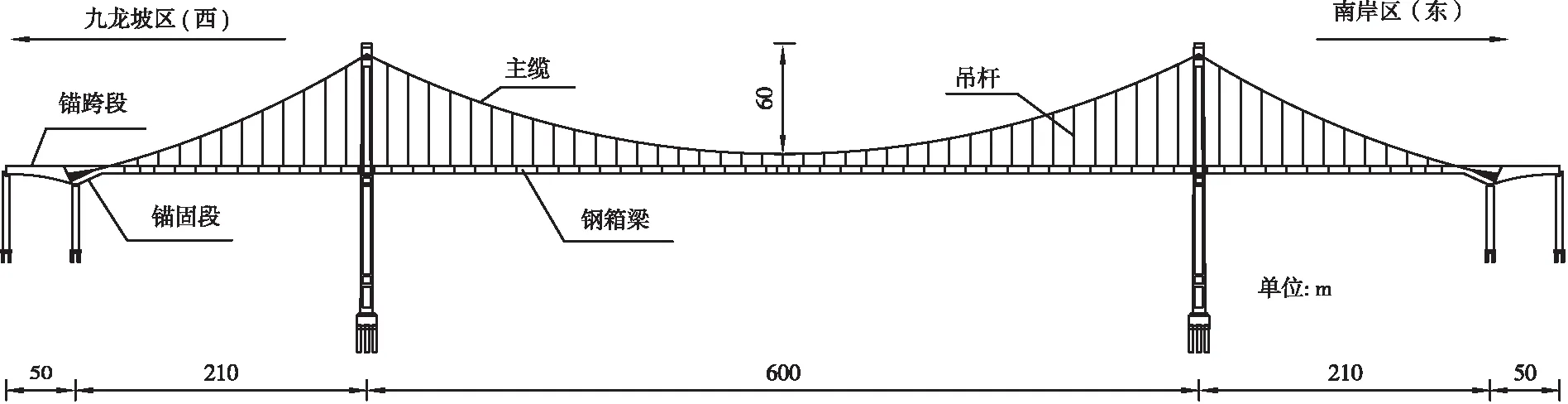
图1 鹅公岩轨道专用桥全桥桥跨布置图

2 数值模型

采用MIDAS/Civil对“斜拉-悬索”体系转换过程进行仿真模拟。结合本桥实际情况，在数值模拟中，主梁、主塔采用变截面梁单元模拟，临时斜拉索、主缆及吊杆采用索单元模拟；主塔塔底固结，主梁于主塔处约束其竖向及横向自由度，主缆锚固点与加劲梁之间采用刚性连接，临时支架采用只受压不受拉弹性支撑模拟。有限元分析模型见图2。

图2 MIDAS Civil 有限元模型

3 主缆位移特性分析

自锚式悬索桥“斜拉-悬索”体系转换最终目标是使成桥线形和受力均符合设计要求，并保证体系转换过程中结构安全。吊索的张拉顺序、临时斜拉索的拆除时机及顺序等使“斜拉-悬索”体系转换方式错综复杂，但体系转换方式是否合理应从施工便利性、安全性、经济性等方面综合进行考虑。本文所采用的体系转换程序是综合以上原则而设置，在整个施工过程中各构件受力及变形均符合要求。

体系转换总体思路：以临时斜拉桥为基础，从主塔向跨中方向安装数对能一次张拉到位的吊索；然后中跨继续向跨中方向安装吊索，与此同时，从主塔向锚跨方向安装边跨吊索，一侧1根，对称安装，直至体系转换完成；再从上至下逐对拆除临时斜拉索，以此实现体系转换。

鹅公岩轨道专用桥桥跨布置对称，在施工过程中主缆变形基本对称，故仅提取左半跨(九龙坡区侧)主缆位移数据进行分析。悬索桥吊索编号及临时斜拉桥拉索编号见图3，体系转换方案施工工序见表1。

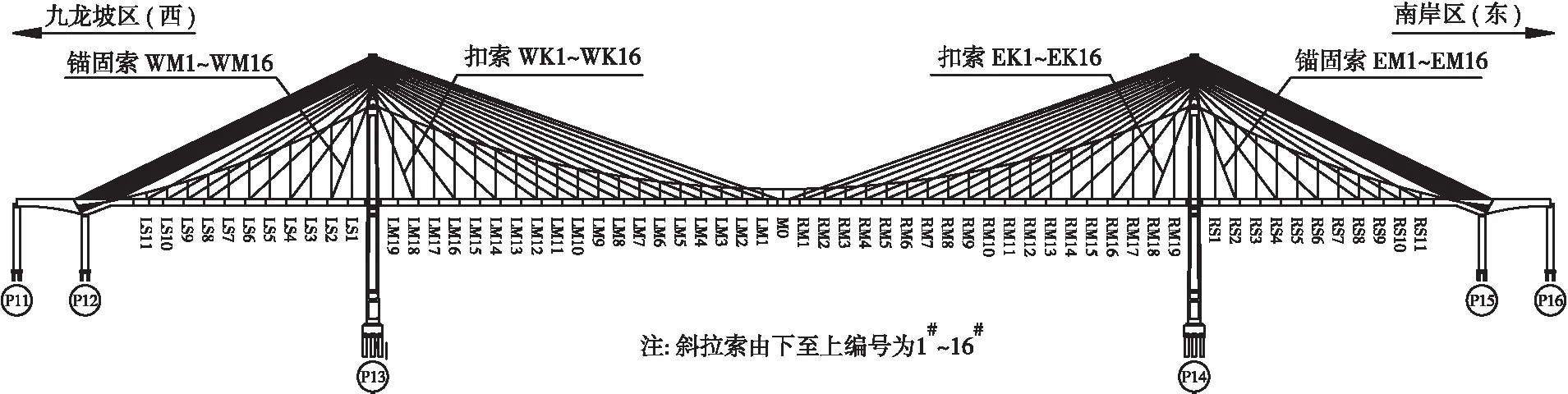
图3 “斜拉-悬索”体系共存图

3.1 主缆位移变形特性分析

为研究主缆位移在各施工阶段的变化规律，选取了左半跨(九龙坡区侧)部分吊索对应主缆索夹点(以下简称吊点)进行位移特性分析，其变化规律见图4，图中“竖向位移累积量”指在当前施工阶段吊索对应主缆索夹点产生的竖向位移累积量。分析结果如下。

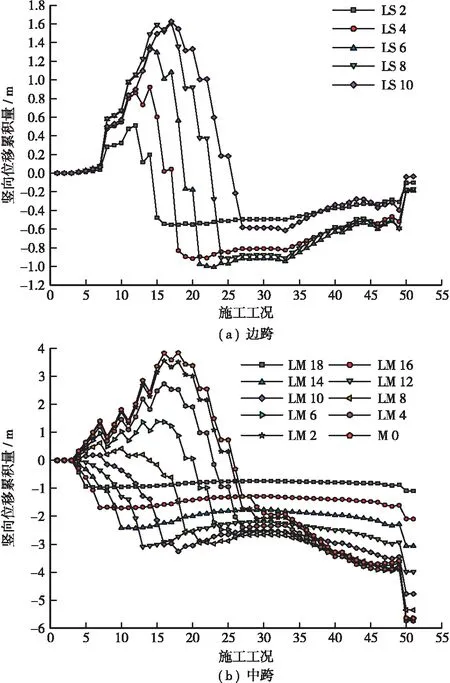
图4 边、中跨主缆竖向位移累积量/m

a.近塔区和主缆锚固区主缆吊点(如LS2、LS10、LM18、LM16)竖向位移波动范围明显小于其他吊点。这是由于近塔区及主缆锚固区的主缆分别受主塔与锚固段的约束作用，主缆的竖向刚度较大，致使该区段主缆竖向变形较小。

b.主索鞍顶推使得两个塔顶主索鞍之间的水平投影长度减小，边跨主缆水平投影长度变大，使中跨主缆呈现出“松弛”状态，而边跨主缆呈现“紧绷”现象，边跨主缆在主索鞍顶推工况均发生了竖直向上位移，中跨主缆位移变化与之相反，如工况8、工况11等。这主要是因为悬索桥施工中鞍座顶推的目的是释放鞍座底由于桥塔纵向刚度约束引起的纵向剪力，避免桥塔受力过大和主缆在鞍座中的滑移，一般悬索桥鞍座顶推前后主缆线形变化不大，但由于本桥先施工了斜拉桥，在张拉吊索时，塔顶的刚度大，塔顶的变形小，鞍座顶推的目的主要是释放鞍座两侧的不平衡力，由此才出现顶推前后主缆线形变化比较大的问题，也即呈现出边跨主缆“紧绷”，中跨主缆“松弛”现象。

c.边跨主缆吊点在拆临时斜拉索阶段均产生了缓慢向上变形的趋势，这是由于临时斜拉索拆除时机位于全桥吊杆张拉结束后，此时加劲梁的绝大部分重量通过吊杆已转移至了主缆，主缆的重力刚度初步形成，因此在拉索拆除阶段，主塔两侧主缆的不平衡水平力较小，主塔向跨中发生了较小的侧移，使边跨主缆发生了较小的向上变形量，中跨主缆竖直向下变形逐渐减小且趋于稳定。此过程中，应根据塔根应力及塔顶侧移及时进行主索鞍顶推，保证主塔安全。

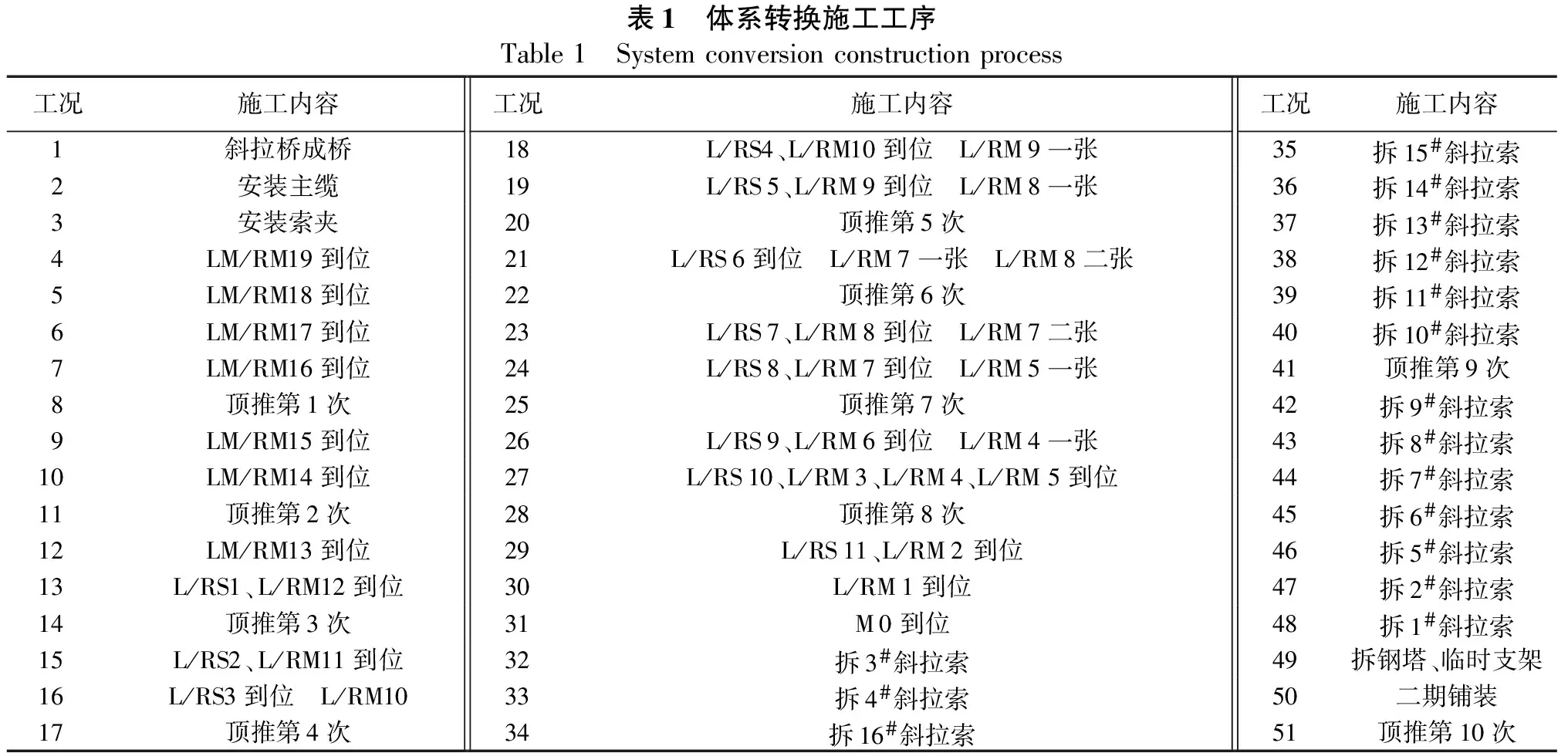
表1 体系转换施工工序Table1 Systemconversionconstructionprocess工况施工内容工况施工内容工况施工内容1斜拉桥成桥18L/RS4、L/RM10到位 L/RM9一张35拆15#斜拉索2安装主缆19L/RS5、L/RM9到位 L/RM8一张36拆14#斜拉索3安装索夹20顶推第5次37拆13#斜拉索4LM/RM19到位21L/RS6到位 L/RM7一张 L/RM8二张38拆12#斜拉索5LM/RM18到位22顶推第6次39拆11#斜拉索6LM/RM17到位23L/RS7、L/RM8到位 L/RM7二张40拆10#斜拉索7LM/RM16到位24L/RS8、L/RM7到位 L/RM5一张41顶推第9次8顶推第1次25顶推第7次42拆9#斜拉索9LM/RM15到位26L/RS9、L/RM6到位 L/RM4一张43拆8#斜拉索10LM/RM14到位27L/RS10、L/RM3、L/RM4、L/RM5到位44拆7#斜拉索11顶推第2次28顶推第8次45拆6#斜拉索12LM/RM13到位29L/RS11、L/RM2到位46拆5#斜拉索13L/RS1、L/RM12到位30L/RM1到位47拆2#斜拉索14顶推第3次31M0到位48拆1#斜拉索15L/RS2、L/RM11到位32拆3#斜拉索49拆钢塔、临时支架16L/RS3到位 L/RM1033拆4#斜拉索50二期铺装17顶推第4次34拆16#斜拉索51顶推第10次

d.在体系转换过程中，中跨主缆竖向位移变形范围较大，边跨主缆竖向位移变形范围相对较小。这主要是因为中跨主缆的竖向位移是主索鞍顶推产生的“松弛”效应和吊索张拉效应的叠加，而边跨主缆竖向位移与之相反，加之边跨矢跨比较中跨小，边跨竖向刚度较中跨大，因此中跨主缆竖向变形表现较边跨更加剧烈。

3.2 主缆位移几何非线性行为分析

大跨径自锚式悬索桥主缆的几何非线性问题尤为突出，研究非线性的方法较多[10-12]，本文采用最为直接的方法-分次加载法对此桥施工过程中主缆几何非线性特征进行分析。分次加载法是以荷载作用不发生改变为原则，探求结构响应的变化规律。具体陈述为在同一结构体系中、同一施工工序下，将同一位置的作用荷载均分为两份，连续两次作用于结构，对比主缆位移的增量。若两次增量相同，则主缆位移呈线性特征；否则，主缆位移呈几何非线性特征。

3.2.1吊索张拉过程中主缆几何非线性行为表现

图5中“两次荷载作用位移差值”指将作用荷载均分为两份并连续作用于结构上时，主缆两次竖向位移增量的差值；各施工工况详见表1；吊点编号为左半跨吊索对应主缆上的索夹点编号，吊点编号按LS11→M0方向依次为2～33；下同，不再赘述。

图5(a)中，施工工况4～工况12主要为对称张拉中跨近塔处的吊索，张拉次序为：LM19→LM13，即从塔根向跨中方向张拉。在此过程中，边跨主缆竖向位移差值最大值从0.2 cm渐渐增至0.7 cm，位移差值的变化量微小；中跨主缆的竖向位移差值最大值随着施工工况的进行从2.1 cm逐渐增加至6.9 cm。以此可知，在施工工况4～工况12过程中，边跨主缆位移几何特性呈现出显著的线性表现形式，但随着施工的进行，线性特征略有衰减；中跨主缆位移线性特性随着吊索的张拉而渐渐弱化。

图5(b)中，施工工况13～工况31为对称张拉边、中跨吊索，张拉顺序为：LS1/LM12→LS11/LM2→LM1→M0。在此期间，边跨主缆竖向位移差值最大值变化历程为：3.7 cm→9.1 cm→0 cm；中跨主缆竖向位移差值最大值变化历程为：10.2 cm→20.9 cm→0 cm；由此表明，随着施工工况13～工况1进行，边、中跨主缆位移几何特性均依次经历了几何非线性特性增强、几何非线性特性弱化、线性特性增强3个阶段。

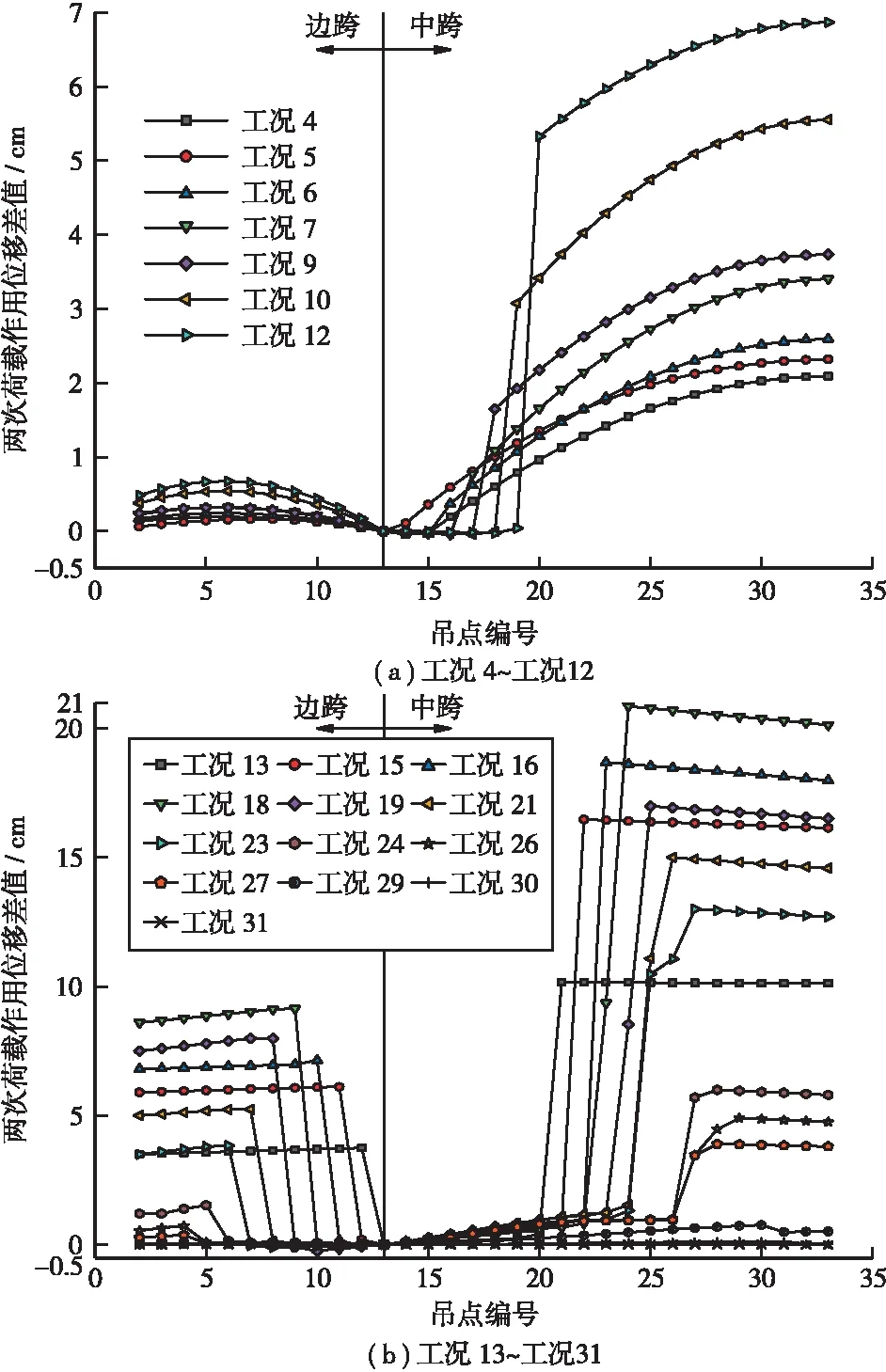
图5 吊索张拉过程中主缆几何非线性特征图(单位：cm)

3.2.2临时斜拉索拆除过程中主缆几何非线性行为表现

采用分次加载法，在吊索张拉完毕后，将临时斜拉索残留的索力等分成2份，历经连续两次卸载将其拆除。通过数值模拟分析得到在临时斜拉索拆除过程中主缆几何非线性随施工工序的行为表征如图6。

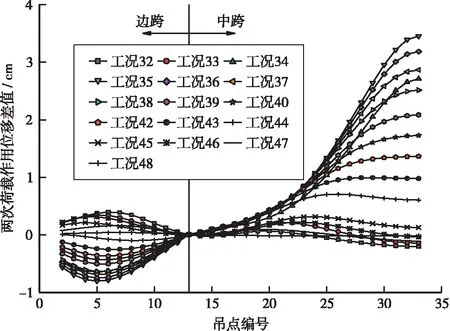
图6 斜拉索拆除过程中主缆几何非线性特征图(单位：cm)

从图6可知，在连续两次卸载作用下，主缆竖向位移差值的最大值随施工工况的历程为：0.7 cm→3.5 cm→0，这表明了在临时斜拉索拆除过程中主缆的几何非线性呈现出“先由弱到强，再从强变弱”的变化规律，但主缆竖向位移差值的量程较小，且“由弱到强”仅持续了3个工况，因此在临时拉索拆除过程中主缆的几何位移特性以线性为主。

3.2.3主索鞍顶推作用下主缆几何非线性行为表现

为了明确了解在主索鞍顶推作用下主缆的几何非线性行为表现，将各顶推量均分成两份，连续两次作用得到各吊点位移差值随顶推工况的变化曲线如图7所示。

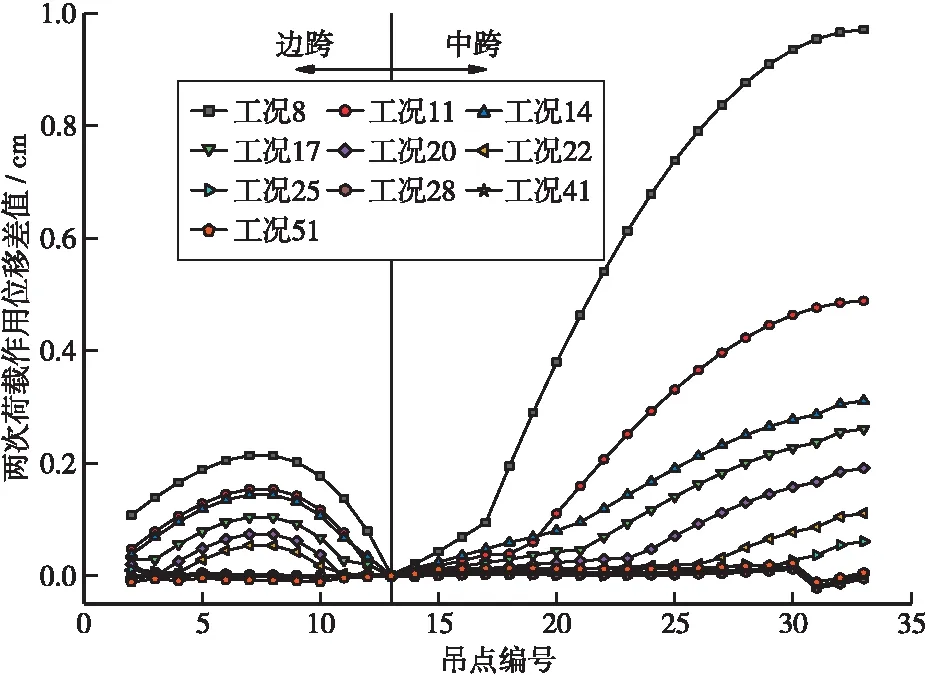
图7 顶推工况作用下主缆几何非线性特征图(单位：cm)

分析图7可知，在主索鞍顶推工况中，通过两次连续相同作用，主缆的位移差值波动范围基本在0～1.0 cm之间，这说明了在主索鞍顶推作用下，主缆位移特性呈现出显著的线形特征。从图中曲线变化趋势可以看出，在主索鞍初始作用到最后一次顶推过程中，主缆的位移差值曲线基本表现出依次下降的变化规律，表明了主缆位移的线形特征在逐渐增强，这主要是由于随着吊索的张拉和临时斜拉索的拆除，主缆的重力刚度渐渐增大，竖向变形增量减小，主缆位移几何非线性特性淡化，线性特性增强。

3.2.4成桥状态下主缆的几何非线性行为表现

为了研究主跨为600 m的超大跨自锚式悬索桥在成桥后主缆的几何非线性行为表现，采用分次加载法，将二期恒载等分为两份，连续两次作用于结构，得到主缆在两次作用下的变形差值见图8。

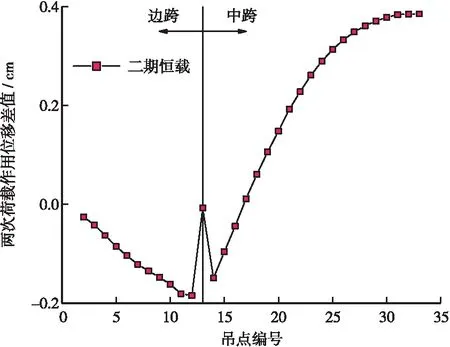
图8 二期恒载作用下主缆几何非线性特征图(单位：cm)

从图8可看出，将二期恒载均分成2份，连续两次作用在主梁上，得到主缆在两次作用下的竖向位移增量，二者差值的变动范围在-0.2～0.4 cm，表明了超大跨自锚式悬索桥成桥后在恒载作用下主缆的位移表现为强烈的线形特性。

4 结论

以鹅公岩轨道专用桥为依托，探讨了大跨自锚式悬索桥“斜拉-悬索”体系转换过程中主缆的位移特性，得出以下主要结论：

a.主索鞍顶推使两主索鞍之间的水平距离减小，即顶推使中跨主缆的水平投影距离减小，中跨主缆呈现出“松弛”状态；边跨主缆水平投影距离增大，边跨主缆呈现出“紧绷”现象。边、中跨主缆位移是主索鞍顶推作用和吊索张拉作用的总效应。

b.在吊索张拉阶段，主缆位移特性主要经历了线性特征显著、几何非线性特征增强、几何非线性特征弱化3个阶段。在体系转换过程中，中跨主缆位移的几何非线性特性比边跨更加强烈。

c.在拆除临时斜拉索阶段，主缆的几何非线性呈现出“先由弱到强，再从强变弱”的变化规律。

d.在主索鞍顶推及成桥恒载作用下，边中跨主缆位移呈现出了显著的线性特征，此时线弹性叠加原理适用。