FAST反射面单元在索网变位中的碰撞分析

李建玲，彭 勃，李 辉，李庆伟，沈宇洲，姜 鹏，罗 斌

(1.中国科学院国家天文台，北京100101；2.中国科学院FAST重点实验室，北京100101；3.中国科学院大学，北京100049；4.东南大学土木工程学院，江苏南京 210096)

500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope，FAST)隶属于国家“十一五”重大科技基础设施项目。利用贵州省平塘县喀斯特地形作为台址，建造世界上最大单口径射电望远镜[1-4]。其反射面采取主动变位的独特工作方式，即主动反射面技术，根据观测目标的不同方向，在500 m口径反射面不同位置，形成300 m照明口径抛物面[5-8]。

500 m口径球面射电望远镜索网形状为口径500 m的球面或300 m的抛物面[9]，有效口径300 m[10-12]。实现反射面的主动变位特性，500 m口径球面射电望远镜采用柔性索网作为反射面的支撑结构，共包括6 670根主索单元及2 225个主索节点[13]。每个主索节点通过下拉索与促动器连接，通过控制促动器实现索网主动变位，形成抛物面或球面。500 m口径球面射电望远镜主动反射面系统主要由圈梁、索网、反射面单元、下拉索、促动器等组成[14]，圈梁、索网总体结构示意如图1所示。整个反射面系统是一个柔性索网+刚性反射面面板的组成结构，反射面单元通过专用连接机构与主索节点连接，铺设在索网上，通过控制促动器调节主索节点实现反射面主动变位。

变位过程中，反射面单元碰撞分析研究是其运行工作的一项重要内容。在此碰撞主要指在某些运行情况下，索网之上与索网连接的相邻两个或多个反射面单元发生接触并相碰，对望远镜索网变位产生隐患的情况。由于500 m口径球面射电望远镜反射面系统组成单元数量庞大，实际变位过程中多种因素耦合作用，加之现场环境、促动器故障等影响，实际可能发生的组合效应很难预知。出于对望远镜运行整体稳定性的考虑，需对变位中反射面单元碰撞问题进行进一步分析研究。

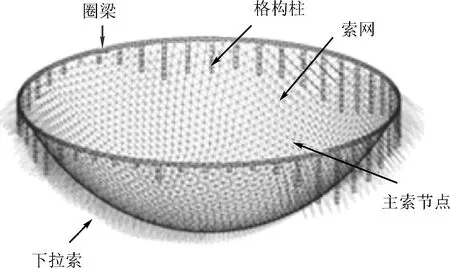
图1 500 m口径球面射电望远镜圈梁、索网总体结构示意图

1 反射面单元碰撞分析

基于索网与反射面单元的结构关系，探讨反射面单元之间发生碰撞的主要因素。在某些变位情况下，主索节点受力产生相对位移，与之相关的主索单元承受应力变化，主索单元长度随之变化，由这些主索单元和主索节点形成的索网空间发生变化，使索网之上与索网相连的相邻三角形反射面单元之间的间距发生变化，从而可能引起反射面单元之间的接触相碰。

变位中主索节点受力能够反映在相关主索单元所受的应力变化上；同时，与索网相连的反射面单元连接机构的位移也在一定约束范围内。可以在反射面单元发生可能碰撞情况下，将主索单元的应力变化值作为限值，进行碰撞分析，得出一种索网变位中判断反射面单元碰撞的方法。从这一角度出发，笔者对单个三角形反射面单元及相关主索单元进行变位前后分析研究。

1.1 反射面单元连接机构与连接关系

500 m口径球面射电望远镜反射面由4 450块反射面单元铺设而成，每块三角形反射面单元通过三个顶点上的自适应专用连接机构与索网连接。整体反射面除与圈梁连接的反射面单元外，其余为三角形。由铝合金结构背架、穿孔铝板以及连接机构等组成。索网变位过程中，索网节点之间会有相对位移，刚性三角形反射面单元的三个顶点位置则相对固定[15]。

反射面单元连接机构自由度设计如图2所示。三角形反射面单元通过三个连接机构(“0”、“1”、“2”)与主索节点相连，三个连接机构均为铰接，完全释放转动自由度。连接机构“0”约束节点的三个平动自由度(Ux=Uy=Uz=0)，连接机构“1”释放节点沿连接杆轴向的平动自由度(Uy=Uz=0)，而连接机构“2”释放反射面单元平面内的两个平动自由度(Uz=0)，在此约束条件下，假定与反射面单元连接的主索节点固定不动，则单个反射面单元为静定结构[15]。其中连接机构“1”沿连接杆轴向的平动范围约为±50 mm。反射面单元与主索节点连接方式如图3所示，三角形反射面单元三个顶点处各有一切边。

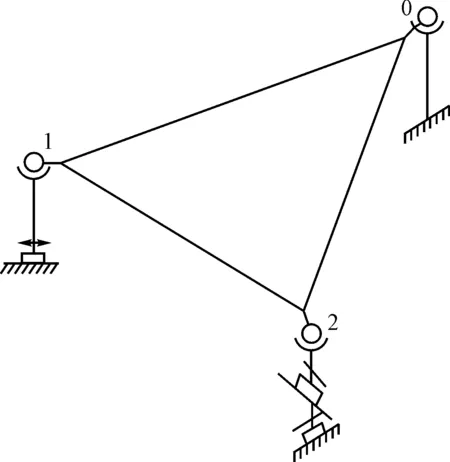
图2 反射面单元连接机构自由度设计

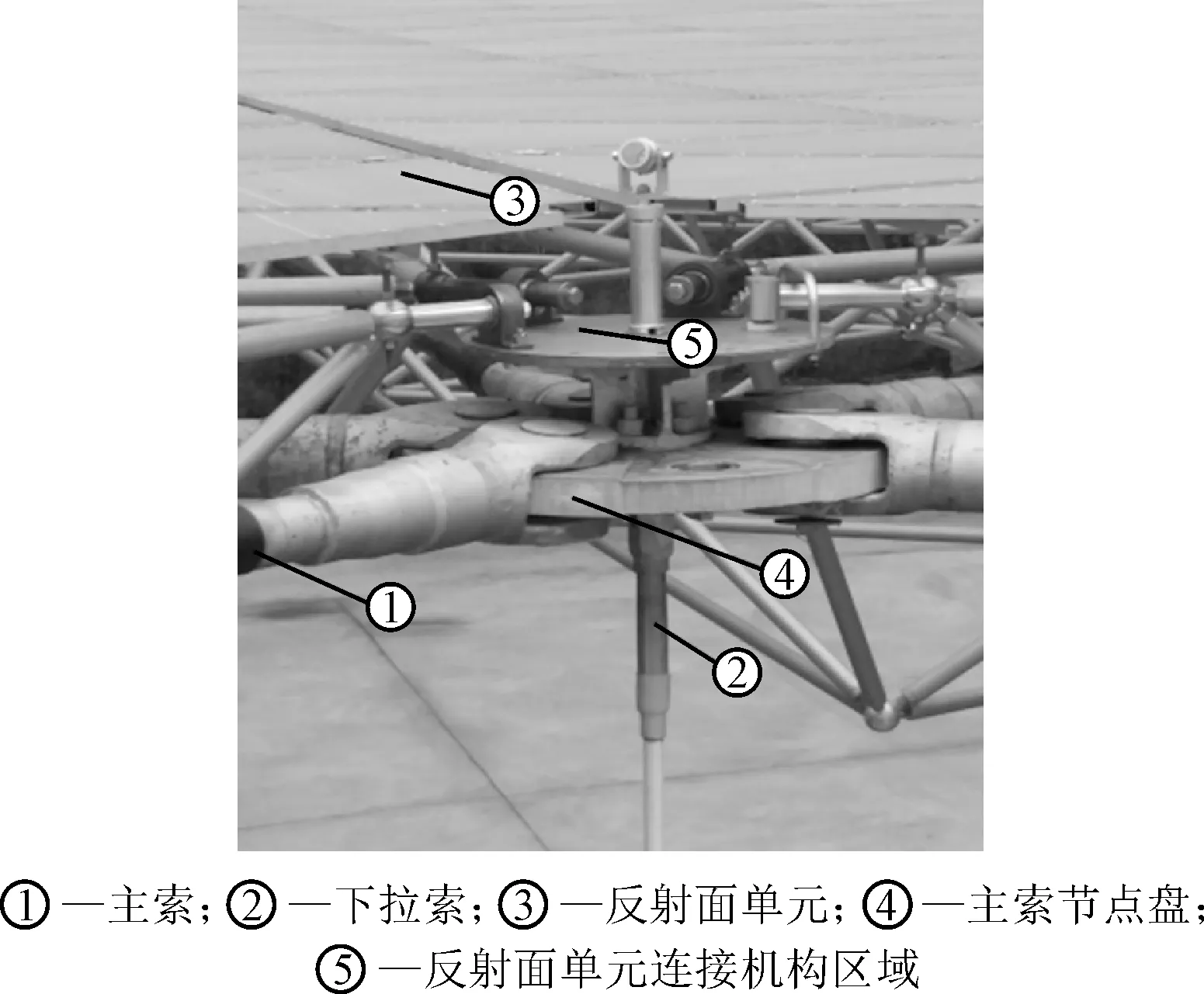
图3 反射面单元与主索节点连接方式

根据几何拓扑关系，对于大多数不在索网边缘的主索节点，有6个反射面单元与之关联，反射面单元连接机构布置在刚性圆盘上，与主索节点相连接，也就是有6个连接机构放置在同一个主索节点盘上部的刚性圆盘上。由于连接机构“1”和“2”释放了相应的平动自由度，两个“1”或两个“2”相邻布置容易出现干涉等，“0”、“1”、“2”号连接机构间隔布置的形式被采纳[15]，反射面单元连接关系如图4所示。连接机构布置示意如图5所示。

图4 反射面单元连接关系

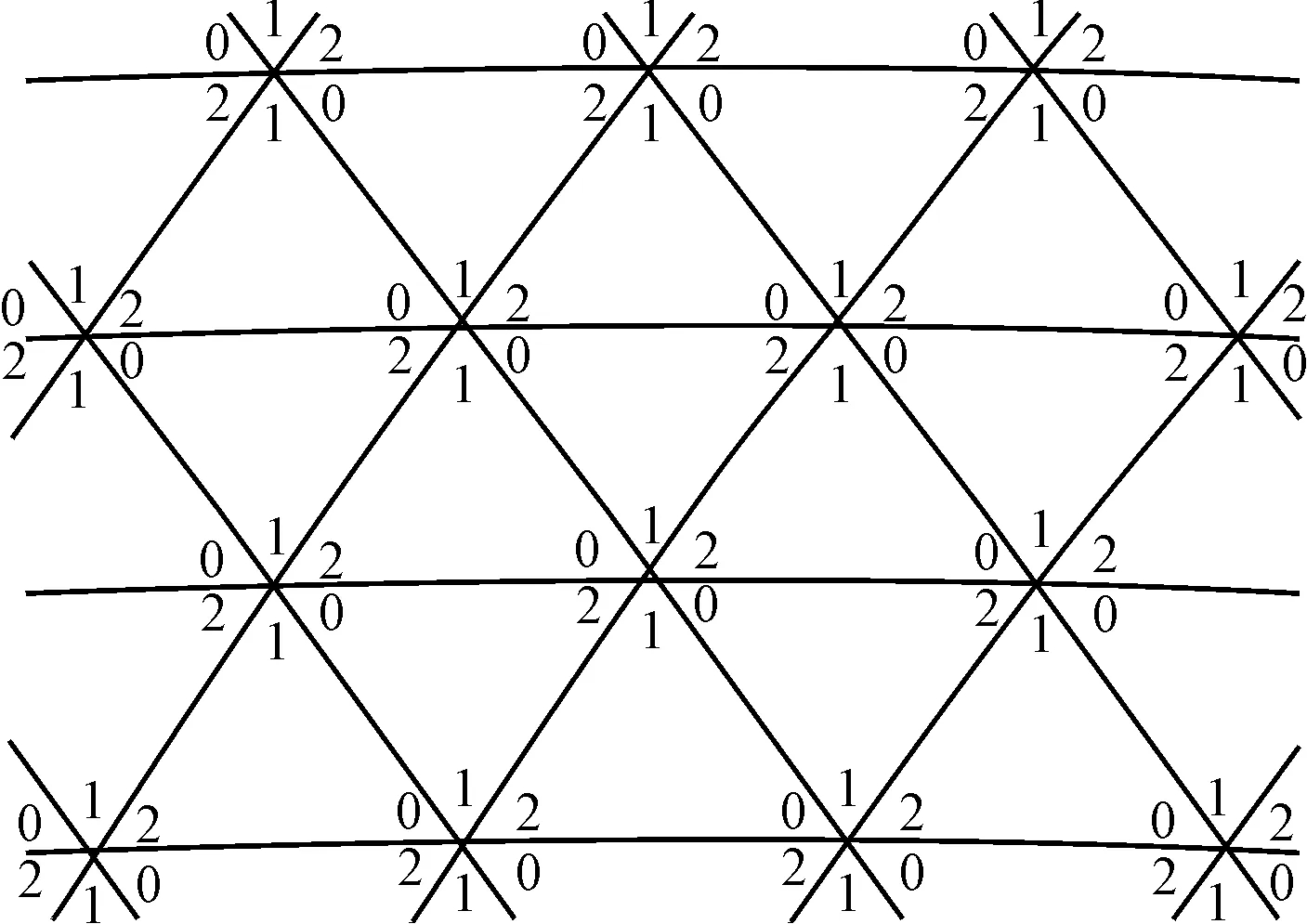
图5 连接机构布置示意图

1.2 基本假定与分析

单个反射面单元与主索单元在变位前及设定变位后的关系示意如图6所示。内三角形表示反射面单元，a、b、c分别表示从三角形顶点处计算的反射面单元各边长。外三角形表示主索单元，A、B、C分别表示三根主索单元的长度。

变位前基准态如图6(a)所示，对于单个三角形反射面单元，图中L表示此时与连接机构“0”对应的主索节点编号，L0表示与连接机构“0”对应的反射面单元三角形顶点处编号，变位后相应的点分别用L′和L0′表示。同理，用M、M1和N、N2分别表示与连接机构“1”和“2”对应的主索节点及反射面单元三角形顶点处编号，变位后相应的点分别用M′、M1′和N′、N2′表示。

d0、d1、d2分别表示与连接机构“0”、“1”、“2”对应的反射面单元三角形三个顶点与主索节点中心投影在反射面平面内节点的连线长度。球面基准态下，d0、d1、d2分别位于其相邻两主索夹角的平分线(平分角如图分别为：∠α/2、∠β/2、∠γ/2)在节点盘平面内的投影方向上。

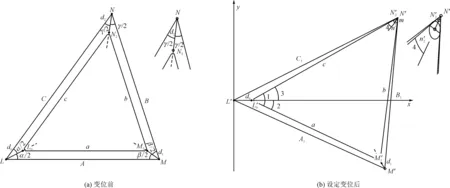
图6 反射面单元与主索单元变位前及设定变位后关系示意图

设定变位，如图6(b)所示，以与连接机构“2”对应的反射面单元顶角切边的中点为圆心做圆，设定变位后，与连接机构“2”对应的主索节点相关联的两根主索单元分别与此圆相切，留有冗余，此时反射面单元与主索单元在反射面平面内的投影处于可能接触状态。若反射面单元越过主索，则可能出现反射面单元相碰风险。在此时的设定情况下进行反射面单元的碰撞分析。

为简化分析计算求解过程，忽略影响较小的因素，做出如下假定：

①反射面单元刚度较大，不考虑其弹性变形；

②主索节点盘盘面基本朝向索网球面法线方向，在运行过程中偏转幅度很小，不考虑主索节点的转动位移；

③结构中，连接机构轴向为相邻两主索夹角的平分线在节点盘平面内的投影方向，由于主索节点盘在实际运行过程中偏转幅度不大，可以认为变位后“0”、“1”号连接机构也位于其夹角平分线上[15]，则上述与“0”、“1”号连接机构对应的d0、d1在变位后也位于其夹角平分线上。

1.3 碰撞模型基本公式

索网作为反射面单元的支撑结构，根据索网与反射面单元的构成关系，球面基准理论状态时，可以认为反射面单元三角形与其关联的主索单元各对应边基本平行，且两者所在平面基本平行。如图6(a)，可以得出球面基准态时，从三角形反射面单元顶点处计算得出的边长a、b、c与相邻主索单元长度A、B、C的关系如下：

(1)

变位时，连接机构“1”发生沿连接杆轴向位移。如上所述，连接机构轴向为相邻两主索夹角的平分线在节点盘平面内的投影方向，故连接机构“1”轴向位移量可以体现在与其对应的d1值变化上。刚性反射面单元的边长a、b、c在变位前后不变，以与连接机构“0”对应的主索节点L′为坐标原点，建立坐标系统。

在此坐标系下，如图6(b)所示，进行反射面单元与主索单元在设定变位后的分析计算。随着连接机构的轴向位移，与连接机构“1”相对应的d1也发生变化。记设定变位后主索单元的长度分别为A1、B1、C1，则依据设定变位后各主索节点的坐标，可计算得出各主索单元的长度，此时可知

a2=(A1-d0cos(α/2)-d1cos(β/2))2+(d0sin(α/2)-d1sin(β/2))2，

(2)

可得A1，则M′点的坐标为

(3)

则依据∠α/2，∠β/2，可得M′1的坐标；依据a、b、c及M1′的坐标，可求得∠1，∠2以及∠3，c不变，可得N2′的坐标。

如图6(b)所示，n2′为与2号连接机构对应的反射面单元三角形顶角切边的中点，可求出∠4，则依据∠3、∠4 、N2′点的坐标以及N2′到n2′的连线长度m，可得n2′坐标

(4)

以n2′为圆心做圆，此时计算主索单元L′-N′、M′-N′与圆相切，可得主索单元L′-N′在当前坐标系下的斜率kL’-N’，则反射面单元与主索单元在反射面平面内的投影可能接触。另取M′点为坐标原点建立坐标系，横、纵坐标方向不变，可得主索单元M′-N′在此坐标系下与圆相切的斜率kM’-N’，两根主索单元相交于N′点，则N′点在原坐标系下的坐标

(5)

依据设定变位后L′、M′以及N′的坐标，可分别得出主索单元A1、B1、C1的长度分别为

(6)

则可以分别得出不同d1值在变位后对应的三根主索单元的长度变化量ΔA=A1-A,ΔB=B1-B，ΔC=C1-C，同时可以求出三根主索单元与基准态比较的应力变化值为

(7)

其中，E为每根主索单元材料的弹性模量。

2 碰撞判别准则

基于索网与反射面单元的结构关系以及合理假定，若反射面单元越过主索在反射面平面内有投影，则可能出现相碰风险。另外，考虑长期循环往复变位对主索应力以及索网疲劳的影响，上述设定变位后，计算出的每组主索单元应力值需满足

(8)

同时还需满足

(9)

其中，σA、σB、σC分别为主索单元的应力值，σA=ΔσA+σA0，为变位后应力变化值ΔσA与球面基准态时的预应力值σA0之和。σmax为正常变位主索应力的最大限值，主索材料的抗拉强度约为1 860 MPa[16],取冗余系数为2.5，则主索应力最大限值约为744 MPa；Δ为正常变位疲劳应力幅最大限值，约为500 MPa[17]。

另外，索网在500 m口径范围内连续变位，选取该范围内的550个主索节点作为抛物面中心轨迹，可以在足够精度下，得到主索应力变化历程[17]，进而得到变化历程中每根主索最大应力值σAmax、σBmax、σCmax。同时，每根主索最大应力值与最小应力值的差值小于应力幅最大限值Δ，故σAmax-Δ到σAmax涵盖了当前主索单元变化历程的最小应力值到最大应力值的范围。

若上述设定变位后计算的每一组σA、σB、σC同时满足上述条件，则反射面单元存在相碰可能，将其作为碰撞判别准则。每根主索单元在基准态下的预应力值可通过计算求出。

3 算例与讨论

图7 1/5区域(A区)主索单元及主索节点布置示意图

500 m口径球面射电望远镜主索及反射面单元布置分为A～E五个区，且满足1/5旋转对称。A～E区的主索节点号采用“各区域字母+节点位置编号”的方式编制。由于其对称性，选取1/5区域(A区)，其主索单元及主索节点布置示意如图7所示。根据主索及反射面单元布置形式，选取一典型位置的主索单元以及对应的反射面单元进行计算，图中标出了算例对应的主索单元及反射面单元。

参照1.3节表示方式，计算得出设定变位后，对应于反射面单元的主索单元应力值。由于实际上每块反射面单元及相应主索单元的具体尺寸与长度不完全相同，故对于不同尺寸的反射面单元及主索单元需单独再进行计算。

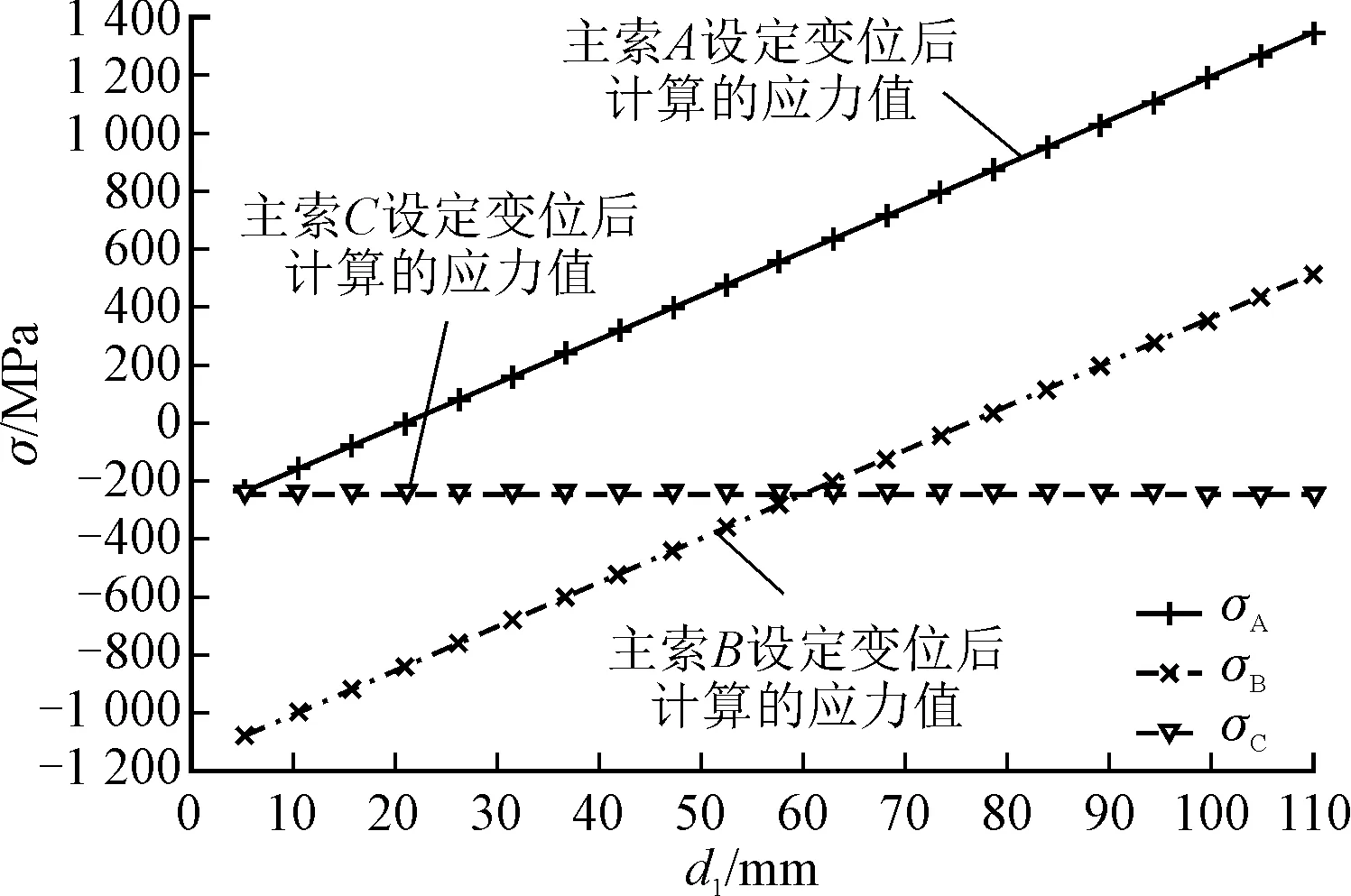
图8 设定变位条件下算例计算的主索单元应力值

基准态时，算例中主索单元三边的长度分别约为11 825.2 mm、11 795.2 mm、12 373.6 mm，取d1的初始值约为60 mm。前述设定变位后主索单元应力值表示为σA、σΒ、σC。设定变位条件下算例计算的主索单元应力值如图8所示。其中σA=ΔσA+σA0,即主索单元A的应力值σA为设定变位后计算出的应力变化值ΔσA与基准态时的预应力值σA0之和，主索B、C同理。基准态时，算例中主索单元A、B、C的预应力值分别约为555 MPa、552 MPa、550 MPa。需将同一对应条件下三根主索单元应力值σA、σB、σC作为一组情况进行分析。

对算例结果进行对比发现，对应于同一个反射面单元的三根主索单元计算出的应力值中，有的主索单元的应力值小于零。由于主索在正常过程中仅受拉不受压，故应力值小于零的情况一般不会出现，且应力值不处于主索应力变化历程中应力值范围之内，不满足2节的条件。基于上述条件的计算方法可作为用于分析反射面单元碰撞的一种方法。

4 结束语

500 m口径球面射电望远镜索网变位过程中，与索网相连的反射面单元的变位是必须考虑的因素。基于500 m口径球面射电望远镜索网与反射面单元结构关系，从构成索网的主索单元变位前后应力的角度来分析反射面单元的碰撞，并从整体反射面系统中提取单个三角形反射面单元及对应主索单元，进行了分析和计算，同时提供了算例。总结如下：

(1)对于文中设定条件下反射面单元算例，基于上述假定及近似计算方法，在主索已有的各安全及疲劳应力设计限值下，正常变位中(不包括促动器故障或失控、连接机构异常、主索及下拉索材料性能参数变化、反射面控制问题或控制异常等)，没有出现碰撞风险。

(2)提出了索网变位中，通过计算主索应力实现对反射面单元碰撞问题分析的方法，为变位整体运行提供冗余保障。

(3)提供了反射面单元在可能出现相碰风险的设定条件下主索应力的近似计算方法。