一种采用冗余性动态权重的特征选择算法

肖利军，郭继昌，顾翔元

(天津大学 电气自动化与信息工程学院，天津 300072)

特征选择的目的是在全部特征中挑选出最具代表性的特征子集，实现数据降维，从而减少后期数据处理所需时间[1]。根据选择策略的不同，特征选择算法可以分为3种[2]：嵌入式、封装式和过滤式。在过滤式算法[3-5]中，信息理论中的互信息是衡量特征关系的常用指标，其中特征间的互信息用于描述特征间的冗余性，特征与类标签间的互信息用于描述特征的相关性，三路交互信息常用于描述特征与类标签间的交互性。

基于互信息的特征选择算法大多通过消除冗余特征、保留相关特征实现特征选择[6-7]。互信息最大化算法[8]将特征与类标签间的互信息作为特征相关性的评价指标，考虑了特征与类标间的相关性，但由于忽略了特征间的冗余性，算法性能不理想。针对互信息最大化算法中存在的问题，互信息特征选择算法[9]、最小冗余-最大相关算法[10]和条件互信息算法[11]，通过引入候选特征与已选特征间的互信息，考虑了特征间的冗余性，性能得到一定提升，但忽略了特征与类标签间的交互性，使目标函数丢失一部分有用信息。因此，一些基于三维互信息的特征选择算法相继被提出。DWFS[12]算法和IWFS[13]算法采用一种动态更新候选特征权重的方法，通过特征与类标签间的三路交互信息度量特征的交互性，取得了不错的结果。但其权重更新系数忽略了对特征间冗余性的考虑，因此算法性能仍有提升空间。

针对该问题，笔者在考虑特征的相关性和交互性的基础上，进一步利用了特征间的冗余性，提出一种采用冗余性动态权重的特征选择算法(Dynamic Weights Using Redundancy, DWUR)。该算法采用一种动态更新特征权重的方法，在每一轮特征选择之后，计算候选特征与本轮已选特征间的对称不确定性及与类标签间的三路交互信息，生成权重更新系数。通过权重计算特征的目标函数值，并挑选目标函数值最大的候选特征。在此过程中，算法同时考虑了特征的冗余性、相关性和交互性信息，以尽量减少目标函数中有用信息的丢失。

1 相关基础

假设X、Y和Z为离散随机变量，候选特征集为F，候选特征fi∈F，已选特征集为S，已选特征fs∈S，类标签为C。互信息表示随机变量X与Y共同享有的信息量，定义如下：

(1)

其中，p(x)为概率密度函数，p(x,y)为联合概率密度函数。互信息表示为熵运算的形式如下：

I(X;Y)=H(X)-H(X|Y) ，

(2)

其中，H(X)和H(X|Y)分别为信息熵和条件信息熵。

大多数特征选择算法将互信息作为评价特征相关性的标准，但与类标签互信息值大的特征并不能保证好的分类结果。互信息会使算法倾向于选择多值特征，缺乏选择的公平性，因此使用对称不确定性描述候选特征fi与类标签C间的相关性，用S(fi;C)表示。其值越大，代表相关性越强，如式(3)所示：

(3)

其中,fi与fs间的对称不确定性代表特征间冗余性系数，用RR(fi;fs)表示。其值越大，特征间冗余性越强。

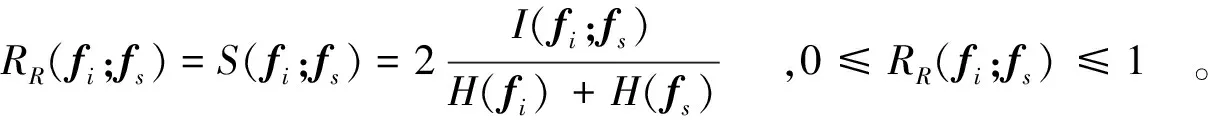
(4)

三维互信息包括条件互信息、三路交互信息以及联合互信息。条件互信息是指在随机变量Z给定的情况下，X和Y之间的互信息，定义如下：

(5)

其中，p(x,y,z)表示随机变量X、Y和Z的联合概率密度函数，p(x,y|z)表示当Z给定时X和Y的联合概率密度函数，p(x|z)和p(y|z)表示当Z给定时X和Y的概率密度函数。条件互信息还可以表示为

I(X;Y|Z)=H(X|Z)-H(X|Y,Z) ，

(6)

其中，H(X|Z)和H(X|Y,Z)分别表示当Z和Y、Z给定情况下，X的条件熵。

三路交互信息表示随机变量X、Y和Z共同享有的信息，其与条件互信息具有如下关系：

I(X;Y;Z)=I(X;Y|Z)-I(X;Y) 。

(7)

基于互信息的特征选择算法一般将fi、fs和C间的三路交互信息作为评价三者之间交互性的指标：

I(fi;fs;C)=I(fi;C|fs)-I(fi;C) 。

(8)

为方便计算，对上式进行归一化，得到特征与类标签间的交互性系数，用IR(fi;fs;C)表示

(9)

当IR(fi;fs;C)取值为正时，fi和fs之间存在交互信息，指在fs给定的情况下，fi能为分类提供更多有效信息，值越大，交互性越强；为负时，fi和fs之间存在冗余；为零时，fi和fs间相互独立，互不影响。

2 采用冗余性动态权重的特征选择算法

假设有候选特征集F，fi∈F(i=1,2,...,N)，为候选特征，N为候选特征总数，设有已选特征集S，fj∈S，表示已选特征集中最近被选入特征。所提算法在每一轮特征选择中，根据fi与fj的交互性和冗余性信息，动态更新候选特征fi的权重系数，该权重系数限制了对应候选特征在下一轮选择中的表现能力，权重越大，表明其与最近已选特征间交互性越强，冗余性越小。特征权重的更新方法为

W(fi)k+1=W(fi)k(1+IR(fi;fj;C))(1-βRR(fi;fj))，k=1,2,...,K-1 ，

(10)

其中，W(fi)k代表候选特征fi在第k轮挑选中的权重，W(fi)k+1代表候选特征fi根据第k轮所选特征fj更新得到的下一轮权重，β为系数项，K代表预先设定的特征选择数目。RR(fi;fj)与IR(fi;fj;C)分别为特征间的冗余性系数和特征与类标签间的交互性系数。

fi与C间的相关性在特征的目标函数中体现，其定义为

JDWUR(fi)k=W(fi)kS(fi;C) ，k=1,2,...,K，

(11)

式中，JDWUR(fi)k代表在第k轮挑选中fi的目标函数值，W(fi)k代表fi在本轮的权重，S(fi;C)为fi与C间的对称不确定性，代表候选特征与类标签间的相关性。由式(10)和(11)可知，算法在考虑特征相关性和交互性的基础上，同时考虑了特征间的冗余性，保证特征的目标函数能最大程度地保留有用信息，消除冗余信息。在每一轮选择中，算法挑选目标函数值最大的候选特征加入到已选特征集S，并将其作为新的已选特征fj，继续下一轮的权重更新和特征挑选，直到所有特征被挑选完毕或特征选择数目达到K。具体执行过程的伪代码如下：

输入：原始特征集X，类标签C，阈值K，候选特征集F

(1)初始化参数：k= 0 ,S=Φ,F=X

(2)初始化候选特征权重：W(fi)1=1 (∀fi∈F,i=1,2,...,N)

(3)for eachfi∈F

(4) 根据式(3)计算各候选特征与类标签间的对称不确定性

(5)end for

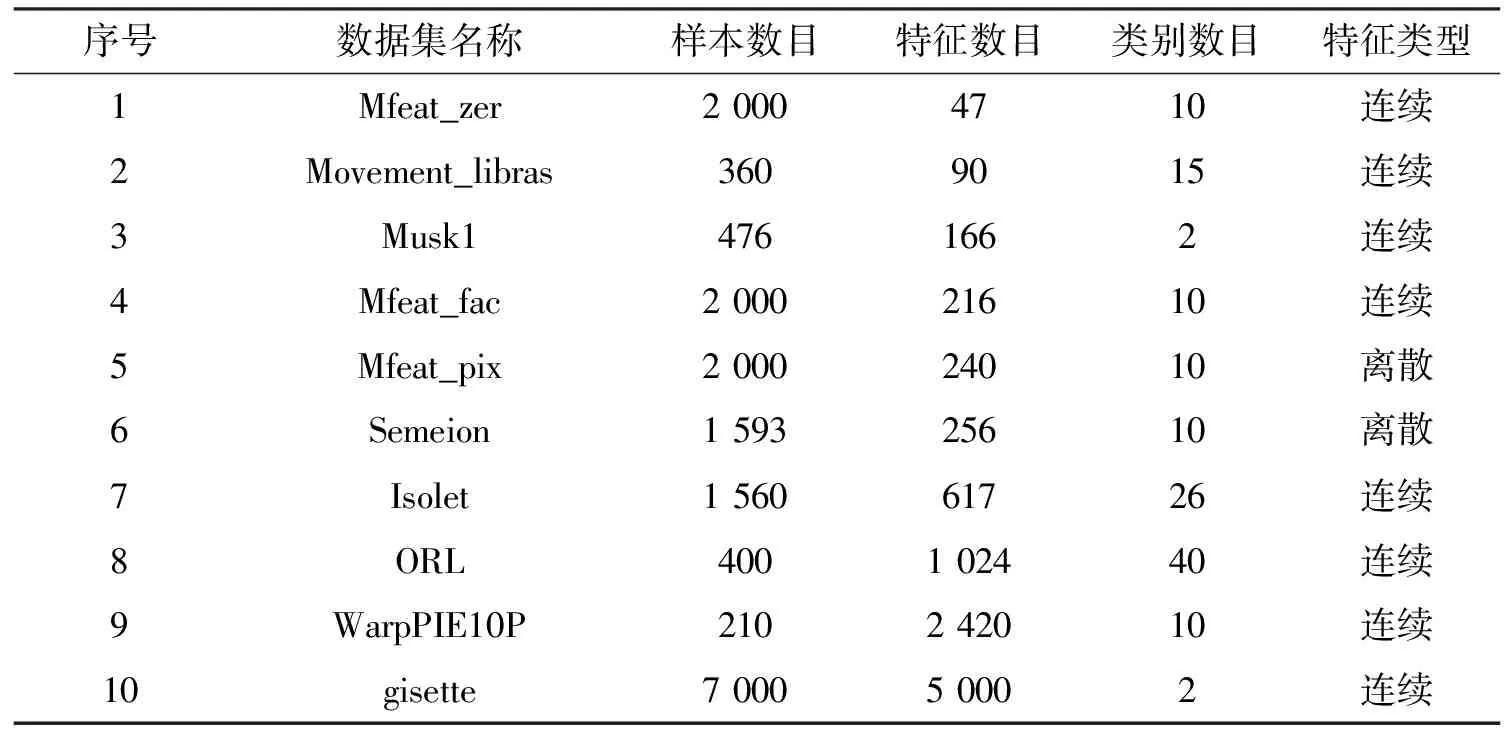
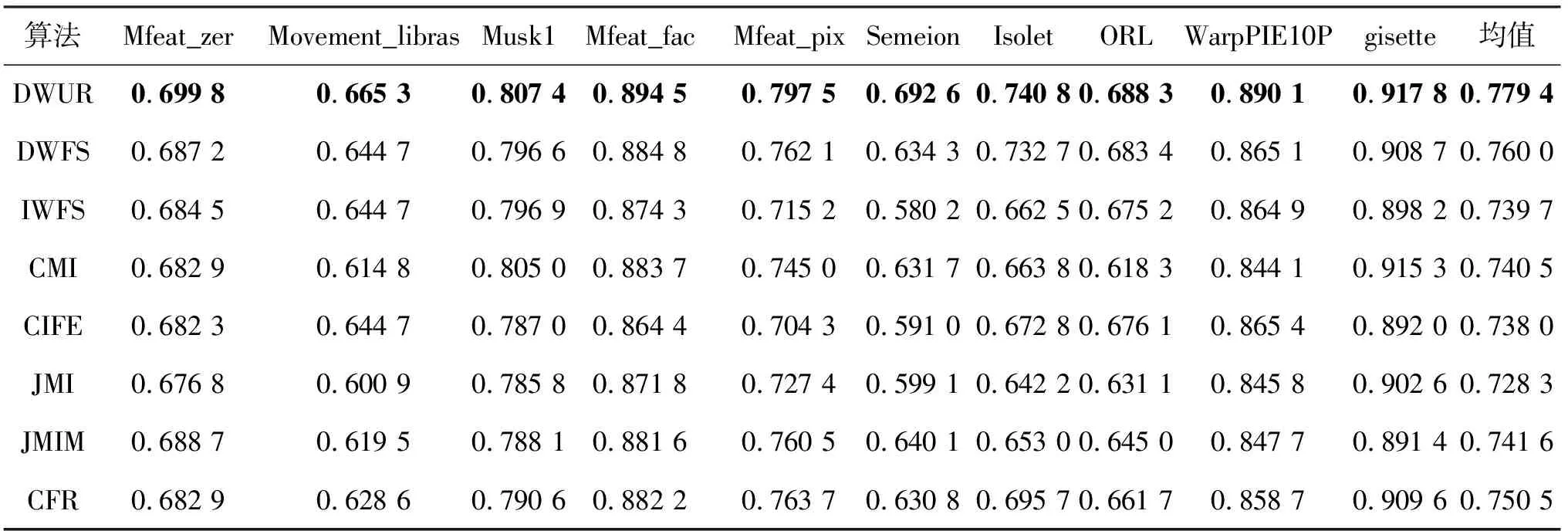
(6)whilek

(7) for eachfi∈F

(8) 根据式(11)计算各候选特征在当前轮的目标函数值JDWUR(fi)k

(9) end for

(11) 将fj添加到已选特征集S=S∪{fj}

(12) 从候选特征集中将fj去除F=F-{fj}

(13) for eachfi∈F

(14) 根据式(4)计算冗余性系数

(15) 根据式(9)计算交互性系数

(16) 根据式(10)更新fi的权重

(17) end for

(18)k=k+ 1

(19)end while

输出：已选特征集S

(1)～(2)行是初始化过程，设置特征选择数目阈值K，已选特征数目k= 0，已选特征集S为空集，候选特征集为原始特征集，候选特征初始权重均为1；(3)～(5)行计算每个候选特征与类标签间的对称不确定性作为候选特征相关性的指标；(6)～(12)行计算每个候选特征在本轮挑选中的目标函数值，并选择最大值对应的特征作为被选特征，加入到已选特征集S中；(13)～(19)行根据本轮挑选结果，动态更新候选特征集剩余特征对应的权重，用于下轮选择中目标函数的计算。

假设原始特征集中特征总数为N，要计算各特征与类别标签的对称不确定性(3～5行)，时间复杂度为O(N)；设已选特征数目为k，则候选特征数目为N-k。在每一轮挑选中，要对每一候选特征计算目标函数值(7～9行)，时间复杂度为O(N-k)；挑选完成后，计算剩余N-k-1个候选特征对应的相关性系数、交互性系数、更新候选特征权重(13～17行)，时间复杂度为O(N-k-1)；当预设的特征选择数目阈值为K时，算法总的时间复杂度为O(NK)。在最坏情况下，当N=K，即依次选取全部特征时，算法时间复杂度为O(N2)。

3 实验研究

在10个数据集上对所提算法进行对比实验，具体数据集信息描述如表1所示。

表1 数据集描述

表1中，前6种数据集来自于UCI机器学习数据集，后4种数据集来自于ASU数据集[14]。实验选用数据集特征数目分布均匀，Mfeat_zer数据集特征数目最少为47，特征集gisette特征数目最多为5 000。样本数目分布为210～7 000，类别数目分布为2～40；除Musk1与gisette为2分类数据集外，其它均为多分类数据集。10个数据集中8个为连续数据集，实验采用MDL离散方法对连续数据集进行离散化。在式(10)中，为保证权重计算结果非负，为交互性系数添加常数项1。为着重考虑特征间冗余性对特征选择性能的影响，对冗余性系数项中的β参数进行多种取值。实验证明，在β=0.5时，算法性能较好，因此实验中β取值为0.5。

利用所提算法和7种基于互信息的算法在上述10个数据集上进行对比实验，对比算法包括CMI[11]、DWFS[12]、IWFS[13]、JMI[15]、CIFE[16]、JMIM[17]和CFR[18]。其中CMI利用特征的相关性和冗余性构建目标函数，其余算法目标函数中引入了三维互信息来考虑特征的交互性。DWFS、IWFS与文中所提算法同属于动态更新权重类方法，其特征选择性能的对比具有代表性意义。

对特征选择结果通过10次10折交叉验证方法，分别利用3种分类器C4.5、IB1和朴素贝叶斯进行分类，并计算3种分类器的平均分类准确率。实验中依次选取前50个特征进行分类，数据集特征数目不足50时选取全部特征进行分类。实验结果如图1所示。其中，横坐标表示依次递增的所选特征数目，纵坐标表示3种分类器的平均分类准确率。

由图1可知，所提算法在10个数据集上均取得了不错的分类结果，说明所提算法对高维和低维、2分类和多分类数据集均具有不错的特征选择性能。值得注意的是，相比于DWFS和IWFS算法，由于所提算法在候选特征权重更新系数中增加了特征间冗余性的考虑，所以在WarpPIE10P、gisette、Movement_libras、Musk1、Mfeat_pix、Semeion这6个数据集上取得了明显优于DWFS和IWFS算法的结果，说明特征间的冗余性是影响特征选择算法性能的一个重要因素。

图1 各算法在10个数据集上3个分类器的平均分类准确率

表2进一步列出了各算法在10个数据集上所有分类准确率的平均值，加粗数字表示在该数据集上达到的最好结果。

表2 各算法在10个数据集上所有平均分类准确率的平均值

表2显示，相比于其他算法，所提算法在所有数据集上分类准确率的平均值均最高。对比于DWFS算法，文中所提算法性能提升明显，进一步说明了在特征权重更新阶段，加入特征间冗余性考虑是有必要的。

表3列出了各算法在10个数据集上所有平均分类准确率的最大值。

由表3可知，文中所提算法在5种数据集上效果达到了最好，而且在另外5种数据集上表现都是最接近最好结果的算法，如在Movement_libras数据集上虽没有达到最好结果，但是其最高平均分类精度为70.80%，基本等于该数据集上达到最好结果的CMI算法的70.81%。

表3 各算法在10个数据集上所有平均分类准确率的最大值

4 结束语

针对基于互信息特征选择算法的不足，提出一种采用冗余性动态权重的特征选择算法。算法除考虑特征相关性和交互性外，还同时利用了特征间的冗余性，以尽可能保证目标函数不丢失有用信息。首先，依据信息理论给出相关性、冗余性和交互性的理论说明和客观评价指标，给出了算法的实现过程；然后，在10种数据集上采用3种分类器同7种相关算法做了对比实验。实验结果表明，相比于其他算法，该算法具有明显的优势。由于数据维度高速增长，探究多维特征间的关系，构建更有效的评价指标将是今后工作的重点。