电源门控技术中的电压噪声优化方案

王磊磊，王 璐

(1.上海科技大学 信息科学与技术学院，上海 201210；2.中国科学院上海微系统与信息技术研究所，上海 200050；3.中国科学院大学 电子电气与通信工程学院，北京 100049)

电压噪声是芯片设计领域一种长期存在的问题，它严重威胁着集成电路的电源完整性[1-2]。电压噪声指当片上供电网络所连接的负载电路发生翻转或者有突然的电流需求时，由于供电网络上的电感、电容和电阻等电子元素的存在，电网上的电压会偏离正常值并持续波动一段时间。随着集成电路技术节点的推进以及低功耗技术如动态电压频率调节的发展，芯片中的电路模块将被较低的供电电压所供给，这将导致电路模块所能容忍的供电电压的波动范围越来越低。因此芯片供电电压的噪声容限在逐步降低，这使得片上供电网络的电压噪声越来越容易达到其噪声容限。当电压噪声超过噪声容限时，芯片中的门电路由于电容充放电速度变慢将不能得到及时的状态切换，从而导致电路模块中时序和功能的错误。所以降低电压噪声是芯片稳定性的重要研究内容，是在芯片设计及芯片运行时期均需考虑的问题。

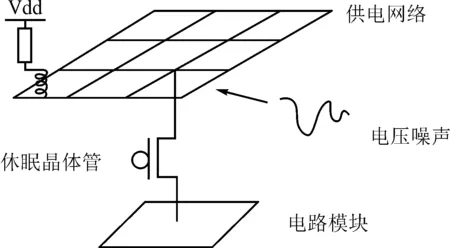
图1 电源门控技术及其引起的电压噪声示意图

与此同时，电源门控技术作为一种集成电路中的功耗管理技术，在功耗问题日益成为集成电路设计中的首要问题的今天，被广泛运用于芯片设计中[3-4]。电源门控技术通过一个休眠晶体管连接电路与芯片上的供电网络，如图1所示。当所连接的电路处于空闲状态时，休眠晶体管会处于关闭状态，以此来避免所连接电路产生的静态功耗；当所连接的电路需要处于工作状态时，休眠静态管会打开，使得电路可以接入电网中，从而正常工作。不幸的是，当休眠晶体管打开时，其所连接电路会突然产生一个瞬时的巨大的电流需求，而冲击电流的需求会在供电网络中引入电压噪声，这种电压噪声将严重威胁着芯片中其他电路模块的正常运行。尤其是当多个电路模块同时接入电路时，所有电路模块产生的电压噪声混合在一起，对芯片功能稳定性的威胁更加严重。因此，电源门控技术所引入的电压噪声应该被严格限制，用以防止影响芯片功能的正确运行。

前人在减小电源门控技术引入的电压噪声方面做了有限的研究，主要分为电路设计层面的工作[5-7]和系统层面的研究[8-9]。在文献[5]中，作者通过联合优化休眠晶体管的设计和供应电压的选取，来减小电源门控电路接入电网时的时间，从而减小能量损失以及电压噪声威胁时间。在文献[6]中，作者通过优化和调制电源门控技术中的休眠晶体管的控制信号，来减小电路中的电压噪声。在文献[7]中，作者提出一种门单元级别的电源门控开关策略，来确定门单元电路的开启顺序，从而减小系统噪声。在文献[8]中，一种额外的转换开关作用于去耦合电容，当去耦合电容所在的本地电网被电源门控技术关闭后，去耦合电容能通过转换开关接入到全局电网中，从而继续抑制其它活跃的电路区域引入的电压噪声。在文献[9]中，作者提出利用电源门控技术来开关多处理器片上系统的每个处理器单元，通过选定的处理器单元，在受到潜在电压噪声威胁时，提前关闭以及威胁过后打开，使得在消除电压噪声威胁的同时，整个系统的任务执行时间和性能代价最小。

笔者提出一种系统级的电路模块接入电网的时间序列优化方案，使得芯片上待工作的电路模块开启的过程中，引入的总的电压噪声最大值能减小。与文献[7]的工作相比，提出的方案集中在模块级别的开关调控，从而能大幅度节约电源门控技术的资源占用，而且不需要考虑门电路之间的驱动关系；与文献[9]中处理器的运算任务优化工作相比，提出的方案以优化电压噪声为目的，这在噪声容限日渐降低的今天是非常重要的。并且提出的技术还能与文献[5-6，8]中的技术协同作用，起到更好地抑制电压噪声的效果。

1 电源门控技术引入的电压噪声分析

1.1 电源门控技术在系统级电路模块中的应用

图2 系统级电源门控技术在多电路模块中的应用

电源开关技术作用于模块级别的电路如图2所示。在图中，芯片上的电路可以分成许多个电路模块，其中有些模块使用了电源门控技术，如图2中的模块A, B和C；有些模块则没有使用电源门控技术，如图2中的模块a和b。当被关闭的模块通过休眠晶体管的导通而接入电路继续运行时，由于冲击电流的需求会在供电网络中引入电压噪声，这会对供电网络接入的其他正常工作的电路模块(比如非门控模块a，b或者其他已经接入电路的门控模块)产生严重的威胁。

1.2 供电网络噪声分析

供电网络噪声分析是集成电路后端设计中的重要问题。供电网络可以被抽取为一种包含很多电阻电感电容的RLC网络，前人提出了很多的方法[10-11]去求解这个大规模的线性方程组。这些细致的分析方法对精确的供电网络仿真有重要贡献，然而对于系统级的供电网络分析而言，设计者需要快速求解带有若干个电路模块的供电网络分析问题。所以使用更加快速和有效的分析方法[2]对电源门控序列优化具有重要的意义。

供电网络作为线性时不变的系统，其对冲击电流的噪声响应v(t)表示为

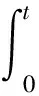
(1)

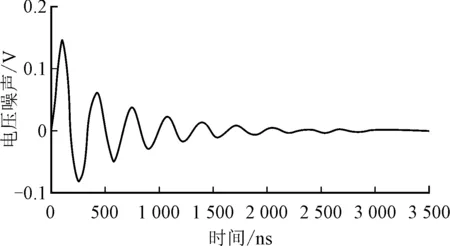
图3 单位冲击电流激励下，供电网络的电压噪声响应

其中,I(τ)表示电路负载在τ时刻的电流值(即供电网络的激励值)，其中τ∈ [0,t]，h(t)是单位冲击电流0时刻作用于供电网络引入噪声的冲激响应。因此，供电网络上的电压噪声可以等效于不同时刻τ的电流的冲激响应在时间t时的线性叠加。如果把时间离散化为一个时间序列，以一个时间窗口Δt为一个时间点，则可以认为τ∈[0,Δt, 2Δt, …,kΔt]，其中,k=t/Δt。根据式(1)，电压噪声可以重新写为

(2)

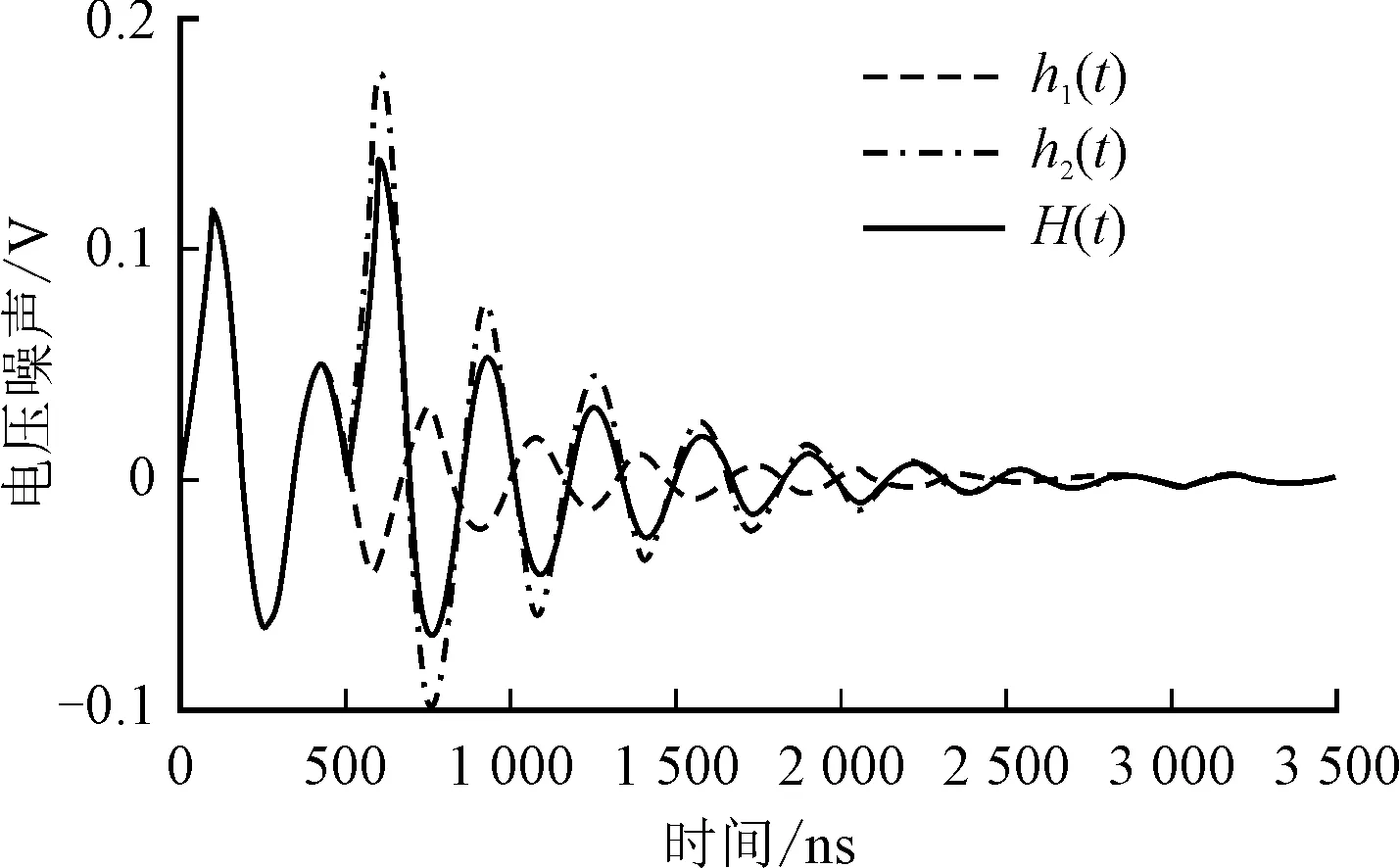
图4 两种电流激励分别引入的电压噪声及总的电压噪声

建立供电网络模型(具体方法见实验章节)，单位冲击电流激励下的供电网络响应如图3所示(Vdd为1.05V)。可以看出，在单次电流激励后电压噪声会衰减并在一段时间之后趋紧于0。根据式(2)，两个电流激励分别产生的噪声以及总的噪声如图4所示。在图中，h1(t)表示在0时间点0.8倍单位冲击电流激励下的系统噪声，h2(t)表示在第500时间点1.2倍单位冲击电流激励下的系统噪声，H(t)表示根据式(2)所得到的系统总的噪声，即所有激励的噪声的叠加值。显然可以看出，系统总的电压噪声可能会比单一激励产生的电压噪声低。这是由于系统中不同噪声响应序列中的正负电压可能会相互抵消的缘故。

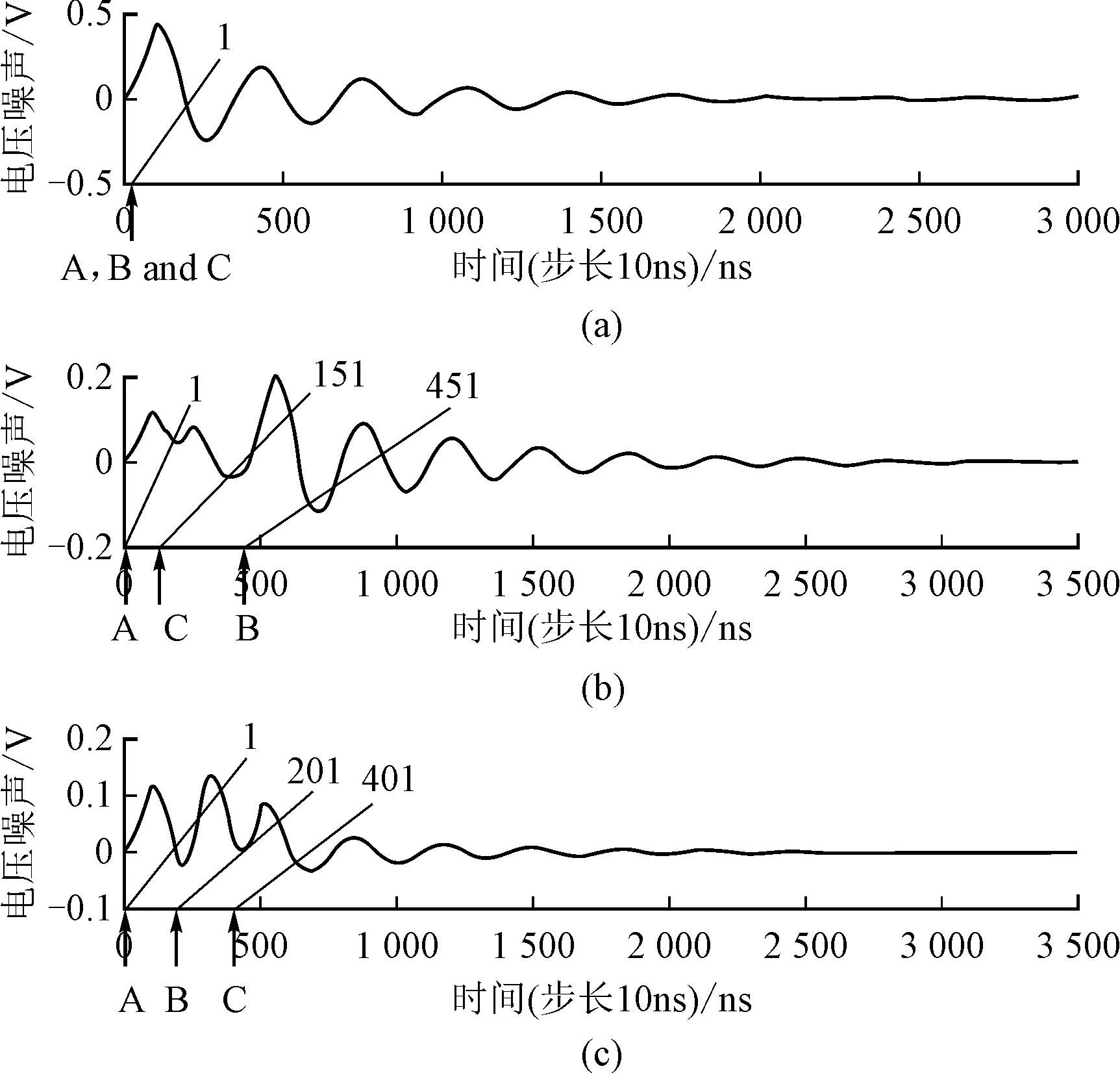
图5 电路模块不同的开启序列会导致电压噪声相差很大

1.3 电源门控技术开启序列对电压噪声的影响

由前两节的分析可知，在系统级的电路模块开关控制中，电路模块不同的开启序列将产生不同的电压噪声。假设以下场景，在图1中所示的系统中，电路模块A, B和C需要通过电源门控技术开启，开启时3个电路模块所产生的冲击电流分别为0.8I0，1.2I0和1.0I0(I0为单位冲击电流的幅度值)。分析3种不同的开启时间序列引起的供电网络上某个观测点的噪声效果，如图5所示。图5(a)中所示为电路模块A，B和C在1时刻同时通过电源门控技术开启，可以看出，由于各个冲击电流的冲激响应叠加，电压噪声接近0.5 V，这甚至达到了供应电压的近50%(Vdd=1.05 V)。在图5(b)中，3个电路模块的开启时间点分别为1，451和151，可以看出，总的电压噪声可以达到0.2 V。而在图5(c)中，3个电路模块的开启时间为1，201和401，总的电压噪声最高不超过0.15 V。因此可以看出，在给定需要开启的门电路后，不同的开启顺序及时间间隔会严重影响供电电压的噪声，其差值能到达惊人的地步。由1.2节的分析可知，总的电压噪声是各个电路模块开启时产生的电压噪声的叠加。这说明，不同电路模块开启时产生的电压噪声不仅是可以部分抵消的，且抵消的程度受这些电路模块的开启间隔所影响。所以电源门控技术的开启序列需要被优化，以使得引入的电压噪声达到最小。

2 问题描述

假设：(1)在供电网络中仅关注少数几个感兴趣位置的电压噪声(即少数几个电路模块挂载点的电压噪声)，这是合理的，因为系统级模型只需关注这些挂载点处的电压安全。特别地，在下文中只研究某感兴趣的点(称为HotSpot点)的电压噪声，全网格的电压噪声响应问题会作为未来的工作进行讨论。(2)在供电网络中，不同位置的冲击电流在HotSpot点产生的噪声响应具有相似的频域特性(如图3所示)，故可使用同一响应序列，这是合理的。因为给定的供电网络会具有特定的频域阻抗[12]。

提出的电源门控技术开启序列优化问题可以描述如下：

给定：(1)芯片中需要通过电源门控技术开启的N个电路模块 {1，2，…，N}；(2)N个电路模块开启时分别产生的冲击电流幅度a1×N=[a1,a2,…,aN]；(3)单位幅度电流激励产生的冲激响应时间序列h1×k=[h1,h2,…,hk] ；(4)完成所有电路模块开启操作的总时间限制为M个时间窗口，这里可以离散出一个时间窗口序列 {1，2，…，M}，其中每一时间窗口都可以进行电路模块的开启工作。

求解：每个电路模块开启的时间窗口mn∈{1,2,…,M} ，其中n∈{1,2,…,N} 。使得在这一过程中产生的电压噪声的最大值Vmax最小。

3 电源门控技术开启序列优化方案

3.1 问题形式转换

由式(2)可知，若第n个电路模块(n∈{1，2，…，N})在tn时刻开启，则其产生的电压噪声在t时刻(t>tn)的值，v(t,n)，可表示为

v(t,n)=an×h(t-tn) 。

(3)

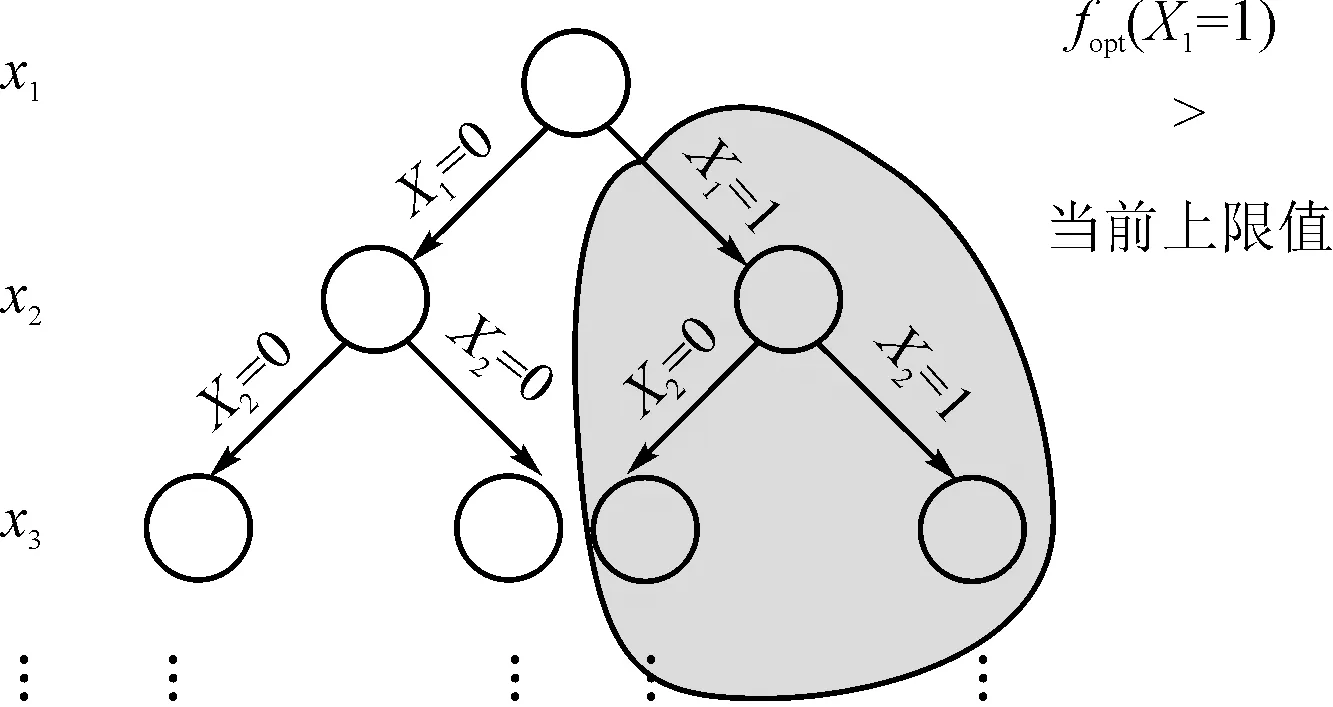
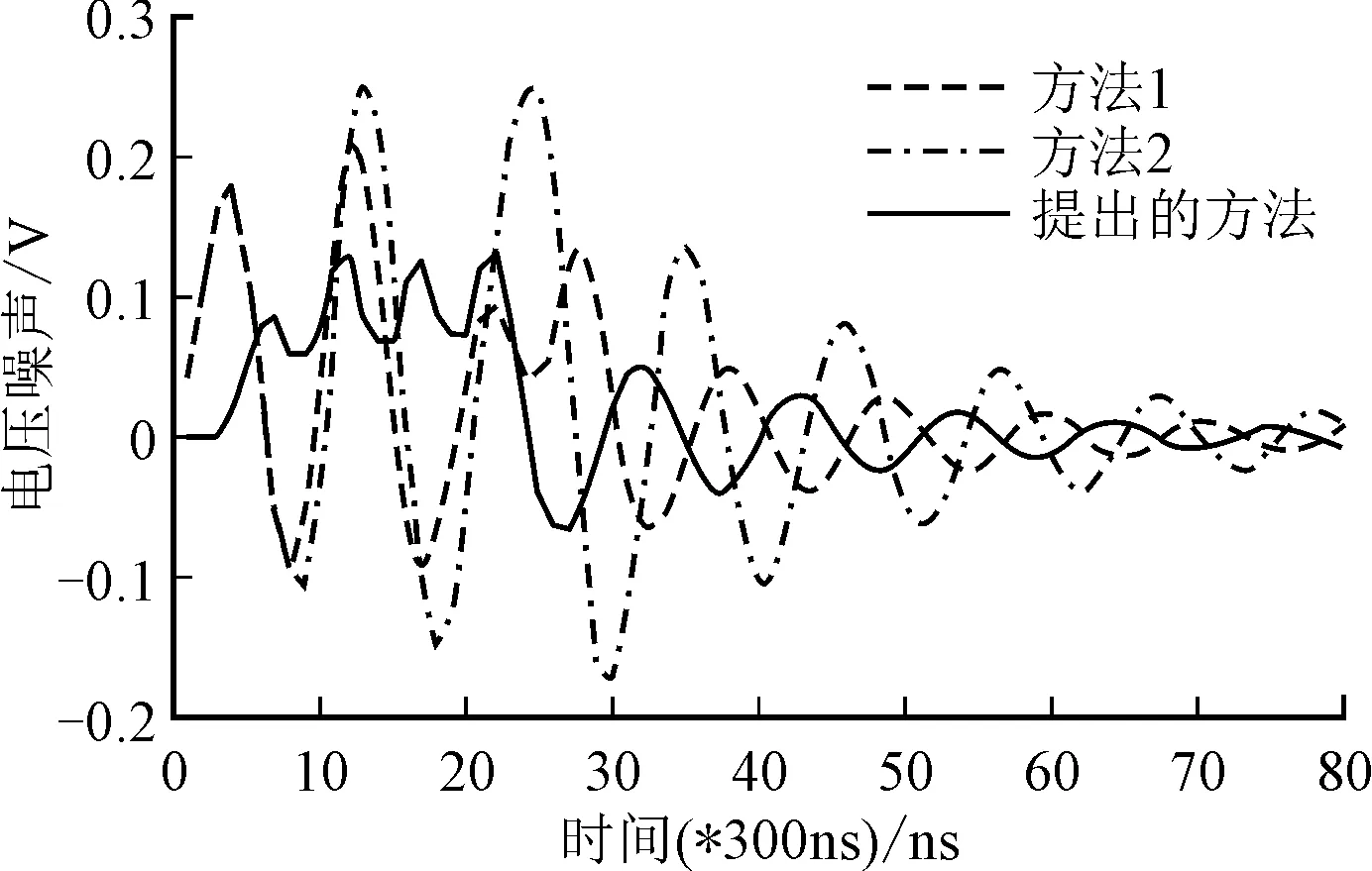
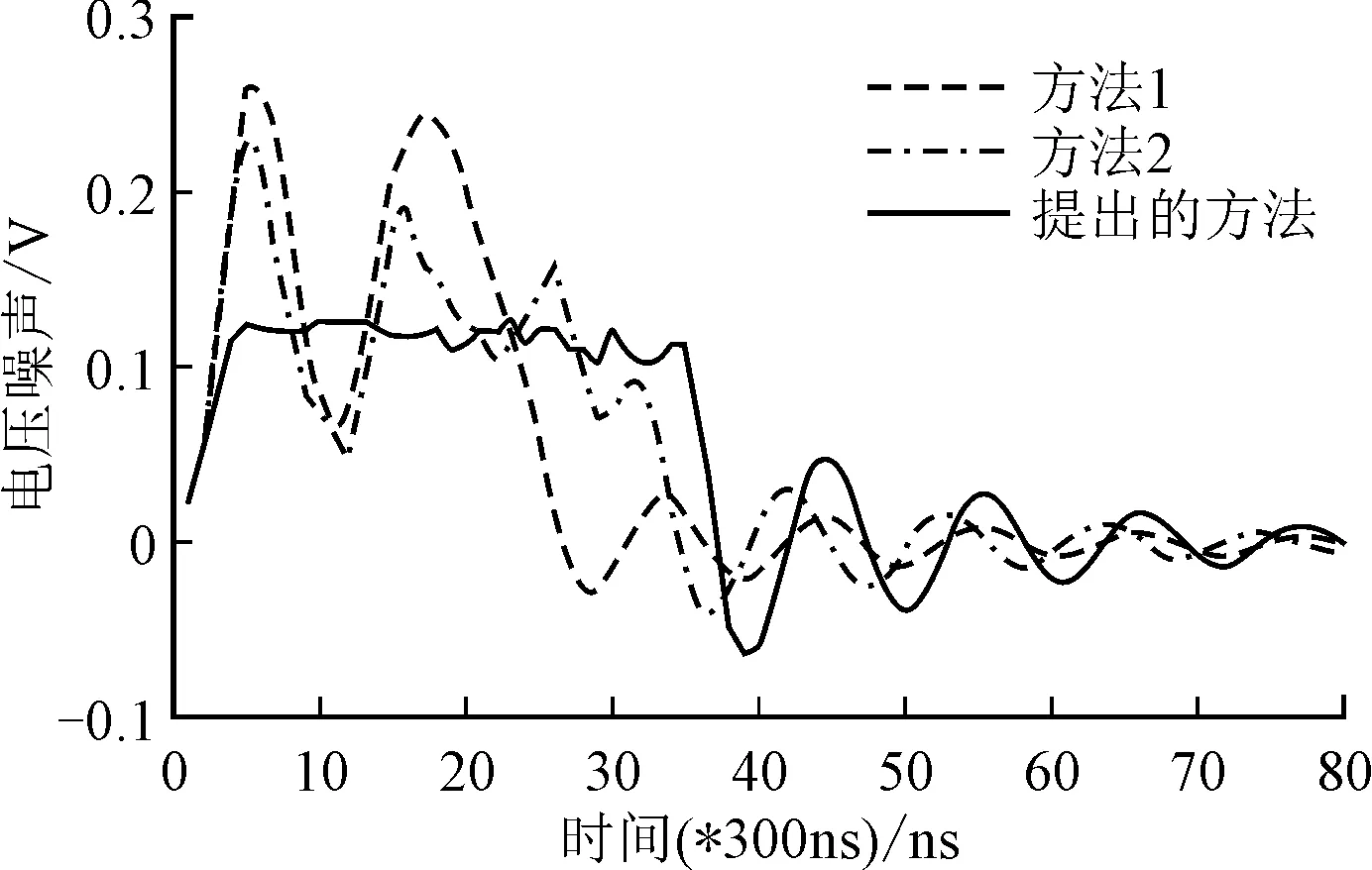
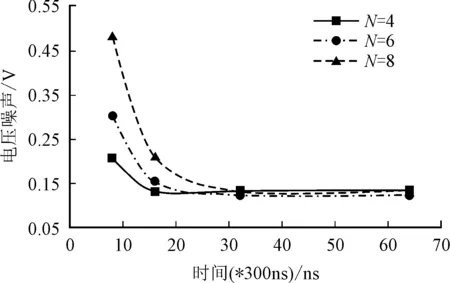
为了保持式(3)在t

(4)

这里设置一个二值变量xm,n来表示第n个电路模块是否在第m个时间窗口开启，若xi,j为1则表示第n个电路模块在第m个时间窗口开启，反之若为0则表示第n个电路模块不在第m个时间窗口开启，其中n∈{1，2，…，N}且m∈{1，2，…，M}。所以总的电压噪声可以表示为

(5)

值得注意的是，式(5)中的Δt表示一个时间窗口的大小(即为步长10ns)，即可认为第n个电路模块在第m个时间窗口开启，其开启时间tn=(m-1)Δt。单位冲击电流的响应序列可以离散化为 [h1,h2, …,hk](见节2问题描述)，则可以用矩阵

(6)

来表示M种在不同时间窗口为起始点的响应序列。用XM×N，即二值变量xm,n所组成的矩阵，来选择其中的N个时间序列，再与N个对应的电流幅度值相乘，可以得出式(5)所示电压噪声在(M-1+k)个时间窗口中的离散值

(7)

用Vmax表示上述噪声序列中的最大值，则优化目标是最小化Vmax。此外在XM×N中，由于每个电路模块只需要被开启一次，需要XM×N的每列变量中有且仅有一个变量值为1(如式(12)所示)；由于每个时间窗口中最多只允许开启一个电路模块，需要XM×N的每一行变量中最多仅有一个变量值为1(如(13)所示)。因此可以给出优化问题：

minVmax，

(8)

约束条件为

(9)

(10)

xm,n∈{0,1} ，

(11)

(12)

(13)

显然，这是一个混合整数线性规划问题(Mixed Integer Linear Programming, MILP)。

3.2 问题求解

求解上节描述的MILP问题，线性规划松弛和分支定界两种技术可以被使用来逐渐获得问题的全局最优解。

图6 分支定界法示意图

求解方法如下：(1)首先线性规划松弛法可以被采用，将所有0/1二值变量松弛成连续变量，原问题即转换成线性规划问题，之后可以通过求解此线性规划问题得出一个实数解，其目标函数的值作为目标函数取值范围的下限；其次可以采用启发式算法获取一个整型解，其目标函数的值作为目标函数取值范围的上限。(2)当解空间不为空时，不断搜寻最优解：(a)当解为实数解时，若其目标函数的取值大于当前上限值，则跳过这个解，并且使用分支定界法缩小解空间；(b)当解为整数解时，若其目标函数的取值小于当前上限值，则更新当前上限值。

分支定界法的示意图如图6所示。二叉树中每个节点表示一个整型变量，其分支代表此变量取不同值。假设图中当x1=1之后其余子孙节点变量松弛成连续变量后，目标函数的最小值依然大于当前上限，则可以直接舍去此分支上的所有解。其中变量的顺序选择可以参考文献[13]。分支定界法可以有效地缩小求解需要遍历的解空间，能增加求解效率。

值得注意的是，在实际的电路模块开启序列优化的过程中，并不需要每次均求解MILP问题。这是因为系统级的电路门控模块的数量往往比较少(典型值小于10，见实验部分)，因此对于常用的电路模块开启序列，可以采用离线计算，提前获得开启序列的最优方案，再将此方案保存到一个查找表中。当需要获取待开启电路模块的开启序列时，可以使用在线查表的方式，来获得开启序列的最优方案，从而节省了重复求解相同问题所产生的开销。举例说明，若图2所示的待开启电路模块A，B和C的最优开启序列，通过事先求解MILP问题可以得到结果为(1，201，401)，则可以把(A，B，C)与对应的(1，201，401)存为查找表中的一条映射信息。当需要开启电路模块A，B和C时，可以通过查找表直接获取其最优开启序列，从而增加优化方案的可实现性。

4 实验结果及分析

实验设置包含单位冲击电流噪声序列的获取和电路模块冲击电流幅度信息的获取，分别为：(1)根据文献[14]中的方法建立了一个5层的片上供电网络，之后抽取其参数并通过宏模型[15]的方法，将含有大规模节点的供电网络压缩成只包含少数连接电路模块节点的网络模型，以便进行快速的噪声序列分析。之后的实验中可以通过spice仿真获取此供电网络在单位冲击电流的激励下的噪声响应序列。(2)通过GEM5仿真器[16]运行标准的SPEC CPU2006测试样例[17]来获取芯片系统运行时的统计计数信息，比如缓存缺失次数，根据这些统计计数信息再用McPAT仿真器[18]来获取电路各个模块的切换时的功耗信息(电流幅度)。之后通过求解MILP问题，可以获取电路模块的最优开启序列。

4.1 开启序列优化在减小噪声上的效果

为了显示提出的开启序列优化方法对减小供电网络噪声上的效果，设置另外两种开启序列的方法作为对比方法：方法1：使用均匀的时间间隔开启每个电路模块，时间间隔为M/N的向下取整。方法2：使用非均匀的时间间隔开启每个电路模块，每个模块开启后的时间间隔与此模块的冲击电流幅度值成正比。

图7和图8显示了两个测试样例的实验结果。分别用3种方法获取电路模块在规定完成时间之内的开启序列，然后获得总的噪声响应曲线。从图中可以看出，提出的方法优化出的电路模块开启序列能大幅度地减少引入的电压噪声。

图7 在32个时间窗口完成时，4个电路模块开启的总噪声

图8 在32个时间窗口完成时，12个电路模块开启的总噪声

在测试样例一中(即电路开启模块为4)，表1展示了提出的方法相比于两种对比方法在减小电压噪声幅度上的表现。可以看出，当约束时间为4个时间窗口(即每个时间窗口都需要选择一个模块开启)时，由于解空间很小，提出的优化方法对比方法1和2仅有2.1%的提升；而当时间约束增加到8以上时，提出的方法能大幅度地减小电压噪声达30%以上。特别地，当约束时间由16增长为32时，提出的优化方法得到的总噪声上限不再发生变化，这表明当约束时间过长时，优化出的开启序列能在较短的时间中就完成开启操作。

表1 当操作的时间约束变化时，提出的方法(标注*)和两种对比方法在总噪声上的表现

图9 最大噪声和约束时间之间的权衡关系

图9展示了最大噪声和完成开启序列操作的约束时间之间的权衡关系(电路模块个数分别为4，6和8)。可以看出，随着约束时间的变长，最大电压噪声可以被优化到一个很小的值。所以当约束时间更长时，提出的方法获得的噪声结果不再发生变化。此外，若要限制电压噪声在一定范围内，提出的方法显示随着待开启电路模块的数量不同，其完成操作的最低约束时间也不同。例如，要限制电压噪声在0.2V，4个电路模块的开启时间至少需要4个时间窗口，而8个电路模块的开启时间则需要至少16个时间窗口。

5 结束语

笔者提出了一种系统层面的电源门控技术的开启序列方案，通过减小电源门控技术打开电路模块时产生的总的电压噪声最大值。通过建立和求解混合整数线性规划问题，可以获得最优的多电路模块在规定完成时间内接入电网的顺序及时间间隔，从而使得引入的电压噪声能最大程度的减小。实验结果表明，提出的电源门控技术开启方案能减小引入的电压噪声达30%以上，并且得到了总开启时间的长短与引入电压噪声的大小之间的权衡。未来可以继续研究的问题包括多模块电路开启时的供电网络全网络的噪声响应分析。