噪声野值下的学生t分布混合CPHD滤波
王明杰,姬红兵,刘 龙
(西安电子科技大学 电子工程学院,陕西 西安 710071)
日益复杂的战场环境对多目标跟踪技术提出了越来越严格的要求,也使得多目标跟踪领域受到更多国内外学者的关注。由于目标会在未知时间和未知地点新生或消亡,因此多目标跟踪的目的不仅需要估计多目标运动状态,而且需要估计时变的目标数目。基于随机有限集[1](Random Finite Set, RFS)的多目标滤波算法因可以避免计算目标与量测之间的数据关联问题而得到广大学者的青睐。由于在滤波过程中联合传递目标强度和目标数概率分布,基于随机有限集的势概率假设密度(Cardinalized Probability Hypothesis Density, CPHD)[2-3]滤波能够获得较高的多目标状态和数目估计精度。因此,势概率假设密度滤波的高斯混合实现(Gaussian Mixture, GM)[3]被广泛应用于各种复杂的多目标跟踪问题[4-5]。高斯混合势概率假设密度(Gaussian Mixture Cardinalized Probability Hypothesis Density, GM-CPHD)滤波通常假设过程噪声和量测噪声均服从高斯分布。然而,在实际应用中,过程噪声与量测噪声难以满足这一假设,尤其当噪声出现野值时,将不再服从高斯分布。野值可以被定义为位于整体分布之外的采样值[6-7]。在多目标跟踪场景中,当目标突然发生系统动态模型无法匹配的机动时,则可认为出现了过程噪声野值。观测目标背景变化、传感器自身的不稳定性将导致量测噪声野值。同时,由于目标散射特性产生的闪烁噪声亦可看作为量测噪声野值[8]。含有野值的过程噪声或量测噪声服从重尾的非高斯分布,GM-CPHD滤波对噪声野值非常敏感,当噪声野值出现时,其跟踪性能会急剧下降,这是由于高斯分布的轻尾特性无法匹配重尾的过程噪声和量测噪声野值。
文献[9]将过程噪声和量测噪声建模为学生t分布,且将目标后验概率近似为学生t分布,从而得到了基于学生t分布的线性卡尔曼滤波[9]并被扩展到非线性系统中[10,12]。但上述方法只能处理单目标场景。文献[13],[14]提出了基于学生t分布的概率假设密度(Probability Hypothesis Density, PHD)滤波,然而,该算法的势估计精度会随着目标数增大而降低。
针对以上问题,笔者提出了学生t分布混合势概率假设密度(Student’s T Distribution Mixture CPHD, STM-CPHD)滤波算法,该算法将过程噪声和量测噪声均建模为学生t分布,并将多目标概率假设密度近似为学生t分布混合形式,利用学生t分布的重尾特性确保在出现噪声野值时目标能够获得一个不可忽略的权值,所提算法可以有效处理噪声野值下的多目标跟踪问题。
1 学生t分布
假设V>0,V∈R,服从分布V~Gam(υ/2,υ/2),其中Gam(α,β)表示形状参数为α>0,尺度参数为β>0的伽马分布。令随机变量z∈Rd,服从均值为0,方差为Σ的高斯分布N(0,Σ)。则
x=μ+(1/V1/2)z,
(1)
其中,服从参数为μ,Σ和υ的多维学生t分布[9,15]St(x;μ,Σ,υ),其概率密度函数可以表示为
(2)
为了方便,笔者用St(x;μ,Σ,υ)来表示式(2)。
2 学生t分布混合势概率假设密度滤波
针对过程噪声和量测噪声导致GM-CPHD滤波性能下降的问题,提出学生t分布混合势概率假设密度(STM-CPHD)滤波。在提出STM-CPHD滤波前,首先需要给出一些基本假设和两条引理。
假设1过程噪声wk和量测噪声vk均服从如下学生t分布:
p(wk)=St(wk;0,Qk,υ1),p(vk)=St(vk;0,Rk,υ2) 。
(3)
假设2每个目标的状态转移函数和量测似然均服从线性学生t分布模型,即
(4)
其中,fk|k-1(x|ξ)和gk(z|x)分别表示转移概率密度和量测似然函数。Fk-1和Hk分别为单目标状态转移矩阵和量测矩阵。
假设3目标的存活概率和检测概率均假设为状态独立的,即
pS,k(x)=pS,pD,k(x)=pD。
(5)
假设4新生目标随机有限集的强度表示为学生t分布混合形式,即
(6)
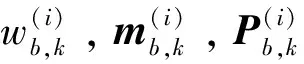
引理1给定F、m、P和Q,且P和Q为正定矩阵,则下式成立:
(7)
引理2给定H、m、P和R,且P和R为正定矩阵,则下式成立,
(8)
其中,
(9)
以上两条引理的证明可以参考文献[9]和文献[10]。
1.STM-CPHD预测
给定假设1~4,假设k-1时刻多目标后验概率假设密度Dk-1和后验势分布pk-1已知,且Dk-1近似为如下学生t混合形式:
(10)
则k时刻预测势分布pk|k-1和概率假设密度分别为
(11)
Dk|k-1(x)=DS,k|k-1(x)+bk(x) ,
(12)
其中,bk(x)由式(6)给出,
(13)
(14)
下面将给出STM-CPHD预测的证明推导过程。
证明:根据势概率假设密度滤波势分布预测公式[3]以及假设3,k时刻多目标预测势分布pk|k-1计算为
(15)
根据势概率假设密度滤波存活目标概率假设密度预测公式[3]以及假设2和假设3,k时刻存活目标预测PHD为
(16)
根据引理1,式(16)可进一步写为
(17)
证明完毕。
2.STM-CPHD更新
假设k时刻多目标预测势分布pk|k-1(n)和预测概率假设密度Dk|k-1(x)已知,且Dk|k-1(x)表示为学生t混合形式
(18)
则k时刻后验势分布pk可由下式计算:
(19)
且多目标后验概率假设密度Dk(x)可以表示为学生t混合形式,表示如下
(20)
其中,
(21)
下面给出STM-CPHD滤波的更新证明。

(22)
根据假设2和引理1进一步可得
(23)
同理,量测更新的概率假设密度Dz,k|k-1(x)表示为
(24)
根据引理2,可进一步得
(25)
因此,可得式(19)~式(21)。证明完毕。
3.矩匹配
由式(21)可知,随着递归算法的进行,学生t分布的自由度会随着递归的进行会无限增大,导致学生t分布混合收敛为高斯混合。所提滤波会因此失去学生t分布的重尾特性,无法处理过程噪声和量测噪声野值。笔者采用矩匹配算法[9-10]解决该问题,按照式(26)来匹配学生t分布的一二阶矩,
(26)
则量测更新部分的概率假设密度Dz,k|k-1(x)可以表示为
(27)
4.状态提取和修剪合并
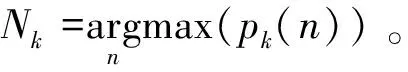

5.STM-CPHD与GM-CPHD的关系
如上所述,当自由度参数趋于无穷大时,学生t分布将收敛为高斯分布。因此,GM-CPHD滤波可以被看做为STM-CPHD滤波的一种特殊形式,证明如下。
证明:当自由度趋于无穷,STM-CPHD滤波中各学生t分布混合将收敛为高斯混合,即
(28)
(29)
(30)
(31)
证明完毕。
3 实验仿真分析
为了验证所提算法的有效性,分别将所提算法与GM-CPHD滤波,学生t分布混合概率假设密度(STM-PHD)滤波[13]对多目标跟踪性能进行对比,并采用最优子模式分配[16](Optimal Subpattern Assignment, OSPA)距离作为性能评价指标。
3.1 参数设置
多目标场景与文献[17]类似,含有野值的过程噪声和量测噪声分别建模为
(32)

3.2 实验结果
图1给出了STM-CPHD滤波、STM-PHD滤波和GM-CPHD滤波在过程噪声和量测噪声野值概率均为0.05时的目标数估计结果。从图1可以看出,本文所提STM-CPHD滤波在过程噪声和量测噪声出现野值的情况下能够获得更精确的目标数估计,STM-PHD滤波次之,GM-CPHD滤波目标数估计结果最差。这是因为GM-CPHD滤波的轻尾高斯噪声假设无法匹配重尾的过程噪声和量测噪声。通过图2所示的STM-CPHD滤波与STM-PHD滤波目标数估计和标准差曲线,可以发现所提STM-CPHD滤波势估计方差明显小于STM-PHD滤波。这是由于概率假设密度滤波只传递了势分布的均值,且其势估计方差会随着目标数增加而增大,势概率假设密度滤波传递的完整后验势分布,进而能够得到更精确的目标数估计结果。
图3给出了STM-CPHD滤波、STM-PHD滤波和GM-CPHD滤波在过程噪声和量测噪声野值概率均为0.05时的最优子模式分配距离。由图3可以看出,GM-CPHD滤波性能最差,这是由于野值的出现致使目标漏跟,导致较差的目标数估计结果,进而增大了最优子模式分配距离。而所提STM-CPHD滤波的最优子模式分配距离整体上低于STM-PHD滤波。这是因为STM-CPHD滤波具有较小的势估计方差,从而能够获得更精确的多目标状态估计。但是在第20,40,60,70,80时刻,图3中STM-CPHD滤波的最优子模式分配距离误差明显大于STM-PHD滤波。这是由于在这些时刻有目标新生和消亡,而势概率假设密度滤波在目标数估计上比较保守,其虽然能保证较低的势估计方差,但对目标数变化不敏感,导致目标数估计在目标新生和消亡时具有一定的延时。
表1给出了STM-PHD滤波、GM-CPHD滤波和STM-CPHD滤波在过程噪声和量测噪声野值概率均为0.05时的平均运行时间。从表1可以看出,STM-PHD滤波所用时间最短,而STM-CPHD滤波需计算势分布,因此运行时间最长。值得注意的是,GM-CPHD滤波与STM-CPHD滤波的计算复杂度理论上相近,但由于GM-CPHD滤波在跟踪的过程中发生目标漏跟,导致其运算时间减少。
为了进一步验证所提算法的性能,实验比较了几种算法在不同过程噪声和量测噪声概率下的平均最优子模式分配距离,如图4所示。由图中可以看出,3种算法性能随着噪声野值概率的增加而下降。GM-CPHD滤波性能下降最快,这是因为更高的野值出现概率将导致目标的漏跟几率增加,进而降低了滤波跟踪性能。所提STM-CPHD滤波优于其他两种方法,这是由于STM-CPHD滤波可以利用学生t分布的重尾特性来更好地处理过程和量测噪声野值,同时具有势概率假设密度滤波对势估计稳定的优点。图4显示当野值概率较小时,GM-CPHD滤波的平均最优子模式分配距离略低于STM-PHD滤波,这是由于势概率假设密度滤波稳定的势估计一定程度上弱化了野值的影响,且概率假设密度滤波本身具有目标数估计不稳定的缺点。

图1 STM-CPHD滤波、STM-PHD滤波和GM-CPHD滤波的目标数估计对比

图2 STM-CPHD滤波和STM-PHD的目标数均值和标准差

图4 STM-CPHD滤波、STM-PHD滤波和GM-CPHD滤波在不同噪声野值概率下的平均OSPA距离对比
表13种算法平均运行时间

算法STM-PHDGM-CPHDSTM-CPHD运行时间/s1.003 53.215 15.171 7
4 结束语
笔者针对传统GM-CPHD滤波无法处理过程噪声和量测噪声野值的问题,提出了一种基于学生t分布的势概率假设密度滤波算法。该算法利用学生t分布来匹配重尾的过程噪声和量测噪声,并近似多目标后验概率假设密度为学生t分布混合形式,得到了势概率假设密度滤波的线性解析解。所提算法是传统GM-CPHD滤波的广义形式,当学生t分布的自由度趋于无穷大时,所提算法将收敛为GM-CPHD滤波。仿真实验表明,所提算法能够有效解决过程噪声和量测噪声下的多目标跟踪问题。下一步工作将考虑将所提算法处理噪声野值下的非线性多目标跟踪问题。

