R语言在统计学教学中的运用
金欣雪
R语言在统计学教学中的运用
金欣雪
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
通过比较R在bagging、随机森林、支持向量机、最近邻、人工神经网络等现代回归方法中所发挥的不同作用,进一步说明了R语言在统计教学中的优势。
统计学教学;R语言;现代回归分析
1 R语言
R语言是属于GNU系统的一个自由、免费、源代码开放的软件,它主要用于统计计算和统计制图[1-2]。它为许多不同领域的工作者提供了丰富的程序包和函数,以及能够满足不同专家学者交流需要的强大社区资源[3]。本文通过一些经典的例子,探讨在统计教学过程中R语言的运用,引导学生掌握应用R语言解决实际问题的方法。
2 R语言在统计学教学中的应用举例
2.1 数据描述
应用举例中所选取的数据为美国波士顿郊区的房价数据,共有506个观测值,14个变量(13个连续性变量,1个分类变量),具体如表1所示。

表1 变量名称及含义
2.1.1 描述数据集的基本信息
首先读入数据:
c=read.table("D:/R/housing2.data.txt",
header=T);
对数据集的基本信息特征进行描述:
summary(c)
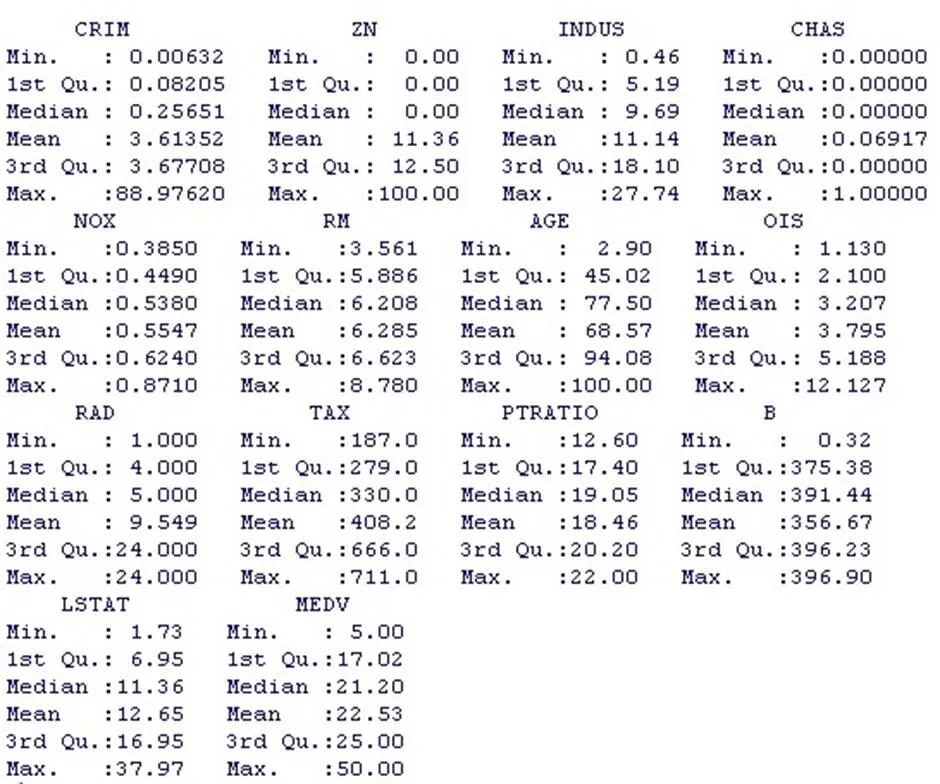
CRIM的均值为3.61,最小值为0.006,最大值为88.98,25%的值小于0.08,中位数为0.26,75%的值小于3.68;
RM的均值为6.29,最小值为3.56,最大值为8.78,25%的值小于5.89,中位数为6.21,75%的值小于6.62;
LSTAT的均值为12.65,最小值为1.73,最大值为37.97,25%的值小于6.95,中位数为11.36,75%的值小于16.95;
2.1.2 绘制变量LSTAT~CHAS,RM~CHAS的箱线图
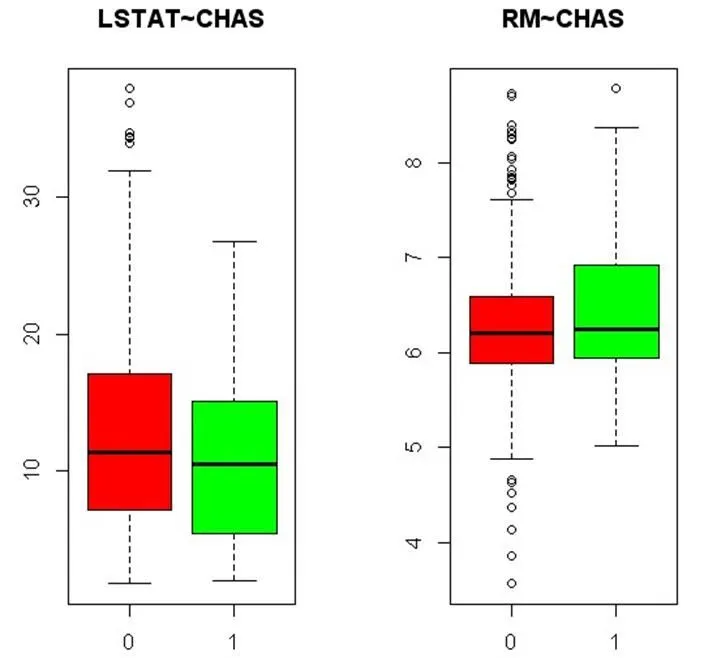
图1 箱线图
par(mfrow=c(1,2))
boxplot(LSTAT~CHAS, data=c, col=c('red', 'green'), main="LSTAT~CHAS")
boxplot(RM~CHAS, data=c, col=c('red', 'green'), main="RM~CHAS")
从图1可以看出,LSTAT的值在CHAS为1时,比CHAS为0时集中;RM值在CHAS为1时,比CHAS为0时分散。
2.1.3 进一步检验变量间的相关性
bb=cor(c[,-c(4)]);bb;#变量间的相关性
symnum(cor(c[,-c(4)]));
kappa(bb,exact=TRUE);#共线性检验

从变量之间的相关程度图中可以看出,大多数变量之间相关程度不高,但某些变量之间的相关程度很大,变量之间存在着多重共线性的影响。
2.2 现代回归与分类
分别按10%、30%、50%分层抽样建立训练集与测试集。通过对三者的比较,利用30%分层抽样建立的训练集与测试集的NMSE最低。在后续的现代分类与回归的方法的研究中,我们均采用30%分层抽样建立的训练集与测试集。
在建立训练集和测试集之前定性变量先因子化:
c$CHAS=factor(c$CHAS)
attach(c);summary(c)
#建立训练集与测试集:
按30%分层抽样建立训练集与测试集
m=506;
val1 <- sample(1:m, size = round(m/3), replace = FALSE, prob = rep(1/m, m))
wsamp3 <- c[-val1,];dim(wsamp3); #选取2/3作为训练集(337*14)
wsamp3;
wtsamp3 <- c[val1,];dim(wtsamp3)#选取1/3作为测试集(169*14)
wtsamp3;
2.2.1 Bagging (bootstrap aggregating)
Bagging通过对训练样本进行放回抽样,每次抽取样本量同样的观测值,所产生的个不同样本生成个决策树,在回归时,因变量的预测值由这些树的结果平均得出[4]。
library(ipred)
bagging.MEDV=bagging(wsamp3$MEDV~.,data=wsamp3)
attributes(bagging.MEDV)
baggingtrain=predict(bagging.MEDV,wsamp3)
baggingpre=predict(bagging.MEDV,wtsamp3)
baggingpre

cat("Bagging训练集上的NMSE为:", mean((wsamp3$MEDV-as.numeric(baggingtrain))^2)/mean((mean(wsamp3$MEDV)- wsamp3$MEDV)^2)," ")
#Bagging训练集上的NMSE为: 0.132 848 2
cat("Bagging测试集上的NMSE为:", mean((wtsamp3$MEDV-as.numeric(baggingpre))^2)/mean((mean(wtsamp3$MEDV)-wtsamp3$MEDV)^2), " ")
#Bagging测试集上的NMSE为: 0.275 671 7
2.2.2 随机森林
随机森林的样本数目远大于bagging。且样本随机,每棵树、每个节点的产生都有很大的随机性。随机森林不修剪每个树,让其尽量增长,以此得出更精确的结果。此外,在大的数据库中的运行很有效率,还能给出分类中各个变量的重要性[5]。
library(randomForest)#调用randomForest包
randomforest.MEDV=randomForest(MEDV ~ ., data=wsamp3, importance=TRUE, proximity= TRUE);
randomforesttrain=predict(randomforest.MEDV, wsamp3)
randomforestpre=predict(randomforest.MEDV, wtsamp3)
cat("randomforest训练集上的NMSE为:", mean((wsamp3$MEDV-as.numeric(randomforesttrain))^2)/mean((mean(wsamp3$MEDV)-wsamp3$MEDV)^2), " ")
#randomforest训练集上的NMSE为:0.032 230 1
cat("randomforest测试集上的NMSE为:", mean((wtsamp3$MEDV-as.numeric(randomforestpre))^2)/mean((mean(wtsamp3$MEDV)-wtsamp3$MEDV)^2), " ")
#randomforest测试集上的NMSE:0.123 473 3
进一步给出分类中各个变量的重要性:
round(importance(randomforest.MEDV),3)
print(randomforest.MEDV);
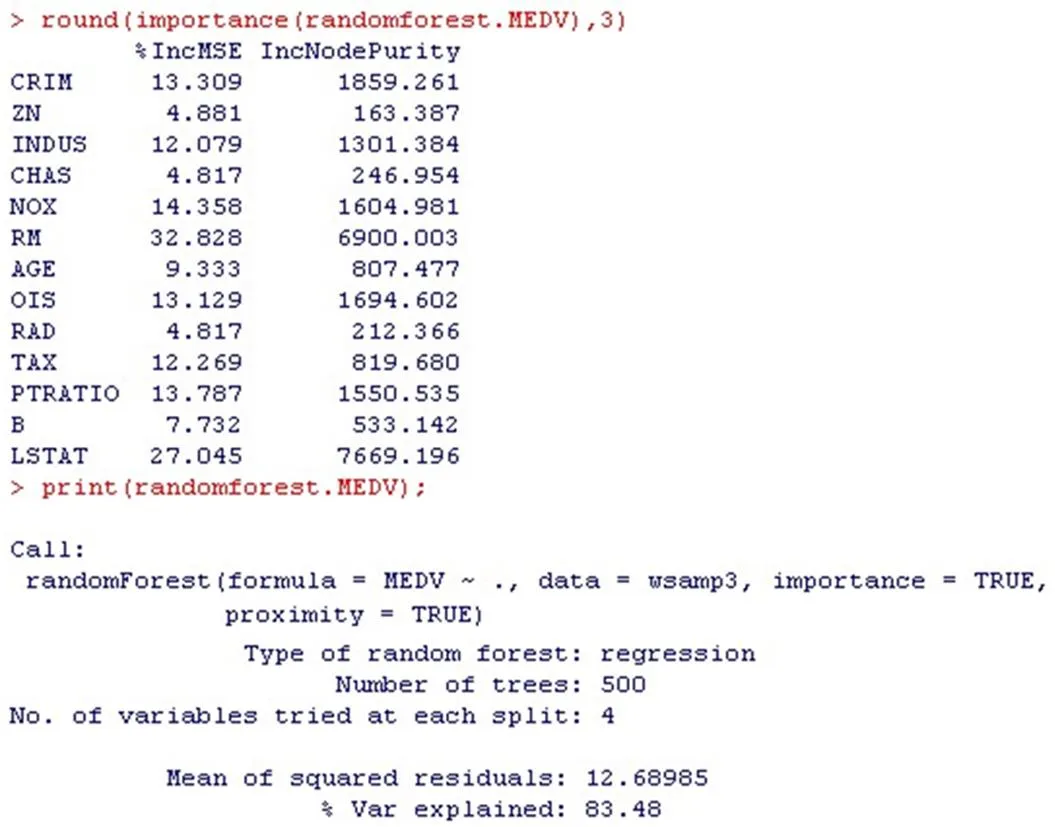
par(mfrow=c(1,2));
for(iin1:2)barplot(t(importance(randomforest. MEDV))[i,],cex.names = 0.7)
图2中左图是用移去一个变量时导致的平均精确度减少来衡量的,右图是用均方误差来衡量的。房间数目(RM)和较低地位人的比率(LSTAT)是最突出的。
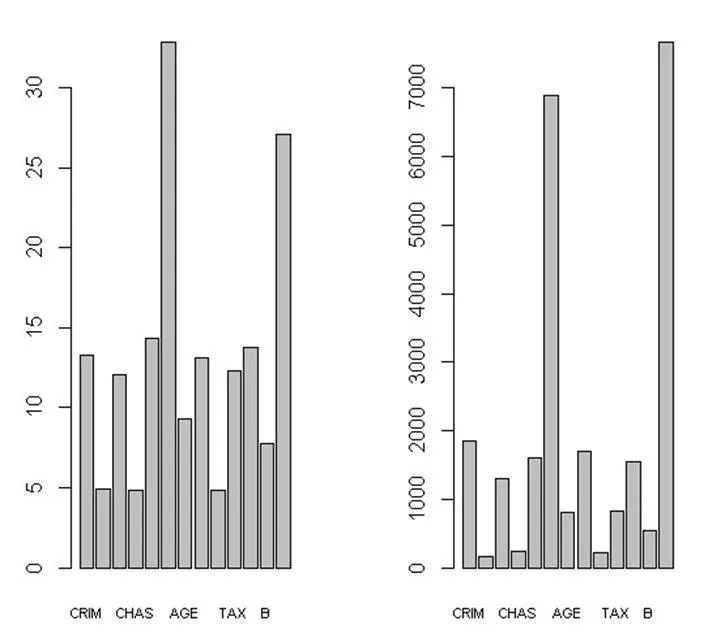
图2 随机森林
2.2.3 最近邻方法
最近邻方法基于训练集对测试集进行分类或回归。在分类中,个训练集点中多数所归属类型决定了距离其最近测试点的归类。在回归中,离测试点最近的个训练集点对应因变量值的平均值即为其预测值[6]。
library(kknn);
a=kknn(MEDV~.,wsamp3,wtsamp3);
summary(a);
kknntrain=predict(a, wsamp3)
kknnpre=predict(a, wtsamp3)
cat("kknn训练集上的NMSE为:", mean((wsamp3$MEDV-as.numeric(kknntrain))^2)/mean((mean(wsamp3$MEDV)-wsamp3$MEDV)^2), " ")
#kknn训练集上的NMSE为:1.632 342
cat("kknn测试集上的NMSE为:", mean((wtsamp3$MEDV-as.numeric(kknnpre))^2)/mean((mean(wtsamp3$MEDV)-wtsamp3$MEDV)^2), " ")
#kknn测试集上的NMSE为:0.274 189 5
2.2.4 人工神经网络
人工神经网络是对自然的神经网络的模仿;可以有效解决很复杂的有大量互相相关变量的回归和分类问题[7]。
library(mlbench);
library(nnet);
dd=nnet(MEDV~., data =wsamp3, size = 2, rang = 0.1, decay = 5e-4, maxit = 1 000);
nnettrain=predict(dd, wsamp3)
nnetpre=predict(dd, wtsamp3)
cat("nnet训练集上的NMSE为:", mean((wsamp3$MEDV-as.numeric(nnettrain))^2)/mean((mean(wsamp3$MEDV)-wsamp3$MEDV)^2), " ")
#nnet训练集上的NMSE为:6.291 331
cat("nnet测试集上的NMSE为:", mean((wtsamp3$MEDV-as.numeric(nnetpre))^2)/mean((mean(wtsamp3$MEDV)-wtsamp3$MEDV)^2), " ")
#nnet测试集上的NMSE为:6.956 288
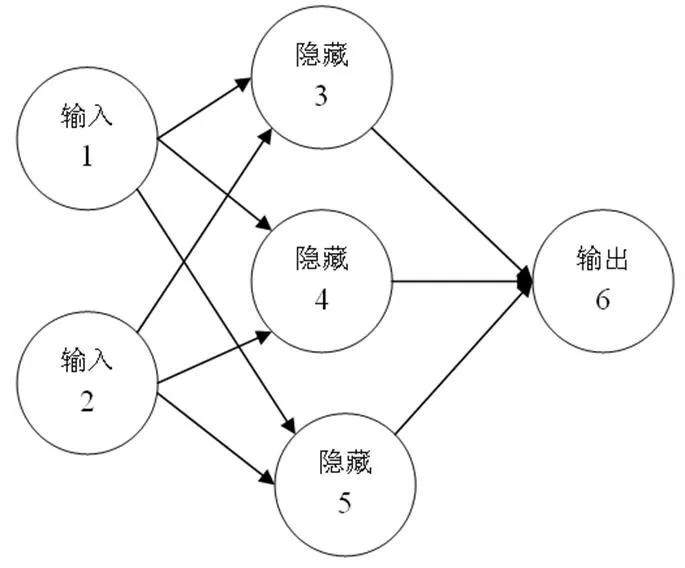
图3 人工神经网路
2.2.5 支持向量机
支持向量机最常用的为最大间隔原则,即分隔直线或超平面两边的不包含观测点的区域越宽越好[8]。
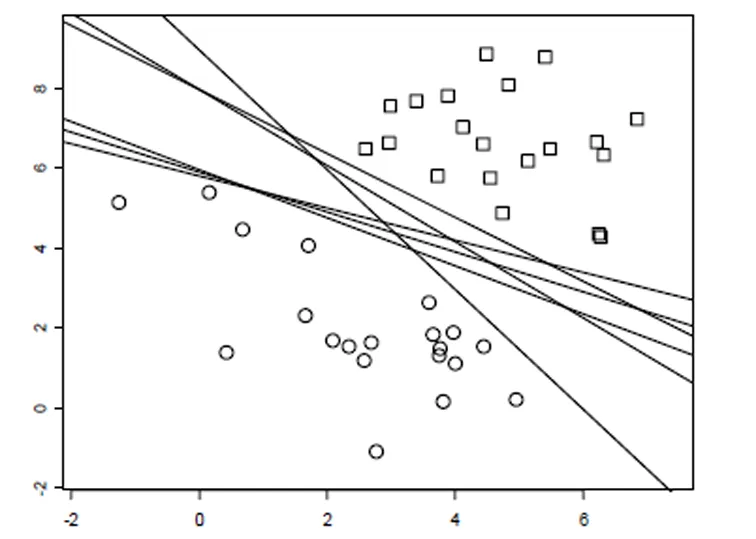
图4 支持向量机
library(mlbench);
library(e1071);
gg=svm(MEDV ~ ., data = wsamp3, kernal= "sigmoid")
e1071train=predict(gg, wsamp3)
e1071pre=predict(gg, wtsamp3)
cat("e1071训练集上的NMSE为:", mean((wsamp3$MEDV-as.numeric(e1071train))^2)/mean((mean(wsamp3$MEDV)-wsamp3$MEDV)^2), " ")
e1071训练集上的NMSE为: 0.090 234 8
cat("e1071测试集上的NMSE为:", mean((wtsamp3$MEDV-as.numeric(e1071pre))^2)/mean((mean(wtsamp3$MEDV)-wtsamp3$MEDV)^2), " ")
e1071测试集上的NMSE为: 0.211 448
2.3 综合比较
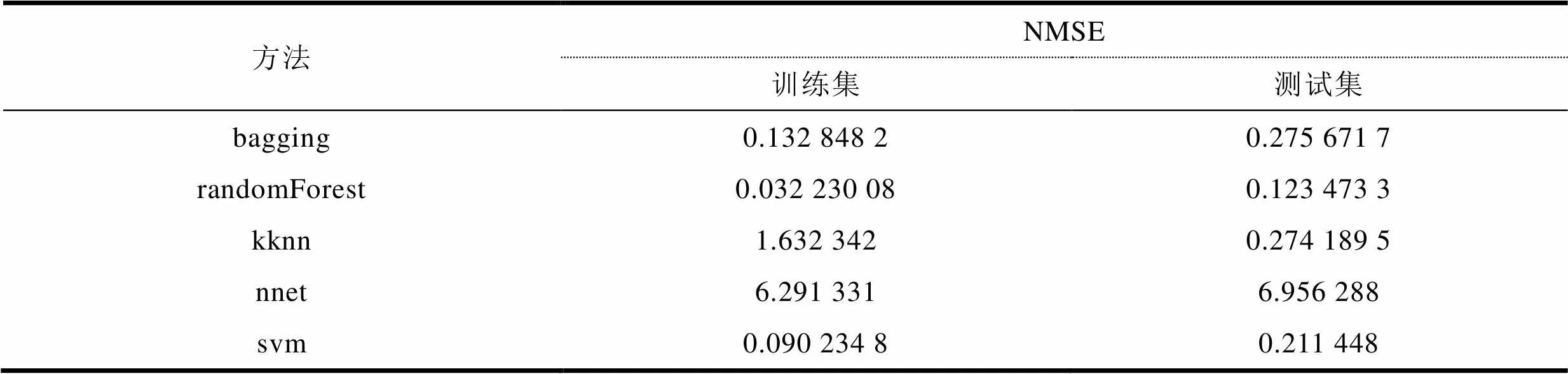
表2 综合比较
表2是采用不同方法处理时得到的NMSE值比较。从中可以看出,randomForest得到的训练集和测试集的NMSE最小,所以randomForest方法更精确。
[1] TORGO L.数据挖掘与R语言[M].北京:机械工业出版社,2013:4-8.
[2] 羌雨.基于R语言的大数据审计方法研究[J].中国管理信息化,2016,(11):46-48.
[3] 李雄英.基于R语言的统计教学应用初探[J].高教学刊, 2017,(1):50-53.
[4] 王斌会.多元统计分析及R语言建模[M].广州:暨南大学出版社,2015:176-187.
[5] 杨霞,吴东伟.R语言在大数据处理中的应用[J].科技资讯,2013,(23):19-20.
[6] 吴喜之.复杂数据统计方法:基于R的应用[M].北京:中国人民大学出版社,2013:195-210.
[7] 汤银才.R语言与统计分析[M].北京:高等教育出版社, 2008:135-142.
[8] 薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007:162-178.
The Application of R Language in Statistics Teaching
JIN Xin-xue
(Department of Mathematics and Statistics, Fuyang Teachers College, Fuyang 236037, China)
The paper combined with examples.discusses the application in the teaching of statistics, compares the different roles R played in bagging, randomforest, svm, kknn, nnet, etc. modern regression methods, in order to further illustrate the advantages of R language software, combined with examples.
statistics teaching; R language; modern regression methods
G642.0
A
1009-9115(2018)06-0049-05
10.3969/j.issn.1009-9115.2018.06.011
全国统计科学研究项目(2017LY63),安徽省哲学社会科学规划项目(AHSKY2018D63),安徽省教育厅重点项目(SK2017A0454),河北省科技厅重点项目(17454701D),阜阳市政府-阜阳师范学院横向合作项目(XDHXTD201709),阜阳师范学院人文社会科学研究重点项目(2019FSSK04ZD)
2018-03-07
2018-05-02
金欣雪(1985-),女,安徽涡阳人,博士,讲师,研究方向为应用统计数据分析。
(责任编辑、校对:赵光峰)

