Heron喷泉水柱高度模型及实验验证
吴亚东,程建荣
Heron喷泉水柱高度模型及实验验证
吴亚东,程建荣
(西北工业大学 理学院,陕西 西安 710072)
利用伯努利方程对喷泉喷水高度的影响因素进行探究,得到最大喷泉高度与瓶中液面高度差的关系。通过实验对模型数据进行了验证。结合影响实验的一些因素,解释了模型假设的合理性。
Heron喷泉;伯努利方程;喷泉高度;准静态过程
早在古希腊时期,一位名叫希罗(Heron)的力学家,利用液体压力作为动力,发明了人类早期的一种喷泉——希罗喷泉。这个相对简单的发明,在当时受到了人们的广泛关注[1]。Heron喷泉通过将重力势能转化为动能从而达到将水从高处转移到低处,而其不需要外加电能驱动,其可以应用场所包括室内小型喷泉装饰、物理演示实验[2]、计时装置、化学反应器等。
1 模型的建立
一般形式的Heron喷泉如图1所示,符号说明见表1。
根据伯努利原理[3-5],同一条流线上各点符合如下关系

沿管1取一条流线,得如下方程:

如果当R>>r时(即使用的瓶子半径远大于管半径),液面B的下降速度b≈0,可化简为:
将上式联立,可解出3管中喷出水的初速度:
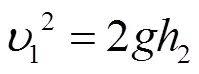
若不考虑水在空气中的运动阻力,即可得到管中喷出水的最大高度:
故可得,=2。
因此,在瓶子半径远大于管半径,液面B的下降速度b≈0,无空气阻力的情况下,Heron喷泉所能喷出的最高水柱与B,C液面高度相等。

图1 Heron喷泉示意图
2 实验设计及结果
为了验证所建立的模型准确程度,进行实验验证,根据Heron的描述,使用热熔胶、电钻、饮料瓶等制作如图2所示的实验装置。
使用此装置进行反复实验,记录下每次的液面高度差与喷泉高度,绘制水柱高度与液面差关系图线,见图3。由图3所得拟合方程为:
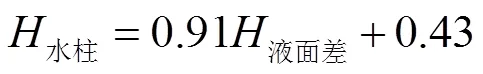
线性相关系数为2=0.98。由此可见,水柱喷射的高度明显与液面差相关,说明建立的模型在一定的误差范围内可以与实验结果相吻合。
图2 实际装置

图3 实验与拟合结果
由于喷水过程中,水柱高度一直在变化,难于准确地测量,因此对图2实验装置进行了改进。在1管子上增长导管,使其内水恰好不喷出,整体的液面处于平衡状态。这样的测量等价于水恰好从管1中喷出(其喷出速度为0时),所以得到较为准确的数据。改进后的装置如图4所示。根据此改进后装置测量结果如图5所示。

图4 准静态测量

图5 改进实验与拟合结果
由图5得到拟合曲线方程为:

线性相关系数为2=0.98。结果进一步证实了所建立模型的合理性。
实验装置的密封性,导管,瓶子之间的连接缝隙都会对测量结果结果产生一定影响,可以使用均匀截面的容器提高实验结果的准确度。
3 模型的数学证明
当喷泉系统处于稳定状态下,一定时间内从B中流入A在流入C的水的体积以及流经1管中的水量相同,即通量一样:

由
得

等式两边对进行微分,有:
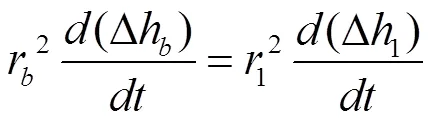
将此方程带入之前所建立的方程组内:

故
由于b>1,因此

4 结论
基于伯努利方程,建立了描述Heron喷泉喷水高度的数学模型,其水柱高度主要由两液面差决定。通过实验验证了所建立模型的合理性,并通过数学推导,从理论上证明模型的合理性。模型的建立使实验过程中的测量更加方便。
[1] 吴家宽.希罗喷泉的制作和讨论[J].物理实验,2001, (8):31-31.
[2] 何建纲,马涛.介绍一种“多级增压式希罗喷泉”[J].物理教学,1993,(12):33-34.
[3] 王旭,苏新兵,胡孟权,等.应用流体力学[M].西安:西北工业大学出版社,2012.
[4] 张永祥.对非惯性系流体动力学问题的研究[J].唐山师范学院学报,1995,(6):13-16.
[5] 郑筱莉.应用“伯努利方程”分析希罗喷泉的喷射高度[J].新疆职业教育研究,2002,10(3):69-70.
Model and Experimental Verification of the Height of the Water Jet in Heron Fountain
WU Ya-dong, CHENG Jian-rong
(School of Natural and Applied Science, Northwestern Polytechnical University, Xi’an 710072, China)
The Bernoulli equation was used to investigate the influencing factors of fountain height. It was deduced that the height of the water jet depends on the difference in liquid level in the bottle. On the basis of theory, massive experiments were designed and carried out, through them the model was in accordance with the experimental results. At the same time, some factors that influence the experiment are analyzed, and the rationality of the model assumption is also explained. Finally, on the basis of experiments and theories, several possible applications of the fountain are given, such as demonstration of physical experiments, interior decoration, timing, and chemical reactors.
heron fountain; ernoulli equation; water jet height; quasi-static process
O301
A
1009-9115(2018)06-0067-03
10.3969/j.issn.1009-9115.2018.06.015
2018-06-22
2018-09-12
吴亚东(1997-),男,满族,北京密云区人,本科生,研究方向为数学建模与材料科学。
(责任编辑、校对:侯 宇)

