混合梁斜拉桥钢-混结合段PBL键数值分析

张 龙,方 志,阳先全,贺绍华

(1.湖南省交通规划勘察设计院有限公司，湖南 长沙 410008；2.湖南大学 土木工程学院，湖南 长沙 410082;3.中交第二公路勘察设计研究院有限公司，湖北 武汉 430052；4.广东工业大学 土木与交通工程学院，广东 广州 510006)

0 引言

混合梁斜拉桥主跨大部或全部采用钢梁，边跨(或部分伸入主跨)采用预应力混凝土梁，通过对钢与混凝土两种材料的合理利用，优化桥梁受力性能，提高桥梁跨越能力和经济性能，钢梁与混凝土梁的连接是其关键技术。目前，采用较多的剪力连接件是传统的圆柱头栓钉，其拉拔性能较好，焊接质量容易保证，同时也存在如抗剪承载力低、疲劳性差、设计受钢筋布置限制等问题[2]。

PBL键最早在1987年由德国的Leonhardt等人提出[3]，从那时开始，国外Oguejiofor和Hosain、M.R.Veldanda和MUHosain等，国内宗周红、李乔、胡建华、刘玉擎、李小珍等研究学者对PBL键进行了大量的试验研究，提出各自承载力参考公式[4-11]。方志、贺绍华等研究表明采用高性能材料RPC(Reactive Powder Concrete)取代混凝土浇筑的PBL键，其受力性能、极限承载力等将得到显著改善[12-14]。

本文以云南某座独塔单索面混合梁斜拉桥为工程背景，基于8组PBL键试件试验结果[1]，采用AN-SYS有限元方法对结合段内PBL键进行数值分析，研究其荷载-滑移、静力学特性及传力机理，并将计算结果和试验进行对比，为混合梁斜拉桥钢-混结合段内PBL键的理论研究和设计分析提供参考。

1 工程背景

该桥上部结构为(81+175)m独塔单索面混合梁斜拉桥，塔梁墩固结体系，桥面全宽32 m，设计荷载为公路-I级，桥型布置如图1所示。主跨采用Q345C钢箱梁，边跨采用C55的预应力混凝土箱梁，设混结合段2 m和钢梁加强段3 m，钢-混结合段设置了上、下钢格室，钢格室的顶、底、腹板及承压板厚均为25 mm，钢格室内填充C55自密实混凝土；结合段内钢与混凝土间的连接采用圆柱头栓钉剪力键和PBL键组合布置，钢格室顶、底板设置Φ22×150 栓钉，其腹板上开有Φ60 mm 圆孔，并穿过Φ25 mm HRB335钢筋，与进入该圆孔的混凝土包裹在一起，钢混结合段构造如图2所示。

图1 桥型布置图(单位：cm)

图2 钢混结合段构造图(单位：mm)

2 试件设计

共设计8组(每组2个)，共16个试件[1]，分别采用RPC和C55混凝土为灌注材料，试件形式及分类如表1所示，

为尽可能真实模拟直接在受力钢板开孔以形成剪力键的形式，国内外倾向采用与实际结构类似的小试件进行单板插入式的加载试验，此方法首先应用于日本鹤见航道桥桥塔钢-混凝土结合段剪力连接件对比试验[15]，后又分别在南京长江三桥[7]、佛山平胜大桥[8]等试验中得以应用，均取得了良好的效果。试验加载以有限元数值分析结果为依据，首先以0.5倍的弹性荷载加载，达到弹性荷载后以0.2倍弹性极限荷载增量一直加载到弹性极限荷载，最后以0.1倍弹性极限荷载增量加载至试件破坏。模型试验及加载如图3、图4所示。

图3 试验模型示意图

图4 试验模型示意图插入式试验加载

表1 试件形式及分类Table1 Specimenformandclassification序号试件编号试件说明灌注材料钢板厚/mm贯通钢筋直径/mm孔径/mm横向配筋率/%1NJ-B-R纯粘结型RPC25—600.642NJ-B-C纯粘结型C55混凝土25—600.643PS-B-R纯隼型RPC25—600.644PR-B-R纯钢筋型RPC2520220.645PB-UB-R无粘标准PBL型RPC2520600.646PB-UB-C无粘标准PBL型C55混凝土2520600.647PB-B-R粘结标准PBL型RPC2520600.648PB-B-C粘结标准PBL型C55混凝土2520600.64

3 有限元建模

3.1 单元离散化

根据试件参数尺寸建立ANSYS有限元模型。混凝土(RPC)块采用SOLID65单元[16]，钢板、贯穿钢筋以及孔间混凝土(RPC)隼采用SOLID45单元[16]，钢板与混凝土(RPC)间摩擦采用COMBIN39单元[16]。各单元离散图如5所示。

(a)混凝土(RPC)块

3.2 材料特性

混凝土和RPC材料的本构模型采用多线性等向强化模型(Miso)[17]，RPC的等效单轴受压应力应变曲线关系根据试验结果[18]，采用分段方程拟合，上升段采用CEB-FIP的模型，下降段为拟合方程，在峰值点符合连续条件。钢板和钢筋均采用多线性随动强化模型(KINH)[17]。

3.3 模型建立

a.模型建立。

以PB-B-C粘结标准混凝土PBL型为例，分别建立混凝土块、混凝土隼、钢板和贯穿钢筋模型。为方便网格划分，先对模型进行切割，通过Lesize定义单元尺寸，设置每条线段数目控制网格的精度，最后进行Sweep扫略。此建模方法不仅使单元整体规整，而且节省了大量计算时间。

b.接触摩擦定义。

由于钢板与混凝土间存在粘结，根据NJ-B-R/C纯粘结型试验[1]，在钢板与混凝土间接触节点建立虚拟连接弹簧单元COMBIN39单元[16]，通过参数KEYOPT(3)=2来设置节点竖向平动，其他方向耦合。弹簧单元的抗剪刚度系数F-D曲线由NJ-B-R/C纯粘结型试验[1]拟合得出，如图6所示。

图6 COMBIN39单元F-D曲线

c.加载及边界条件。

为了保证分析结果收敛和精确，模型采用位移单调加载，即在钢板顶施加位移荷载步，逐级加载，这样更容易精确反映每个PBL键的荷载与位移关系。由于结构对称，仅需建1/2结构模型，并施加对称约束。

d.关键处理。

由于混凝土抗拉强度低，在模型中通过对钢板孔与混凝土隼下半圆节点分离、贯穿钢筋上半圆节点与混凝土分离，而不考虑混凝土的抗拉作用。

在计算过程中，往往在低荷载下，钢板孔内混凝土就被剪坏而钢筋并没有屈服，随着破坏区增多，不平衡力在计算迭代过程中难以消去，往往容易造成不收敛。很多研究学者仅在弹性阶段与试验结果吻合较好，但在塑性阶段却相差很大，主要原因是混凝土隼被破坏后转由贯穿钢筋承担剪力时，大量混凝土隼单元失效，造成计算模型不能收敛[19]。因此，本文关闭了开孔板内混凝土隼单元得压碎与开裂，保证荷载有效由开孔板传递给隼和贯穿钢筋。

PB-B-C粘结标准PBL型半结构有限元模型如图7所示。

图7 1/2结构有限元模型

4 有限元分析

由于篇幅有限，本节仅重点对PB-B-C粘结标准PBL型剪力键受力全过程进行分析。

4.1 线性阶段分析

在位移荷载小于0.3 mm时，构件处于完全弹性阶段，当位移荷载逐渐增加至0.5 mm时，钢板与混凝土间的粘结作用，钢板变形由顶部逐渐减小，内侧较外侧略小，孔内混凝土隼位移有0.28 mm，相应位置贯穿钢筋位移为0.21 mm，端部位移接近于零。应力方面，除孔洞附近应力相对较大外(14 MPa)，其余各应力较小，均处于弹性状态。线性阶段荷载-相对位移曲线如图8所示。

图8 线性阶段荷载-相对位移曲线

虽然在低荷载下结构局部进入了非线性阶段，但对整体结构线性特征影响不大，其抗剪作用主要由混凝上隼与贯穿钢筋共同承担，贯穿钢筋仍为弹性阶段。

4.2 非线性阶段分析

当位移荷载达15 mm时，混凝土隼竖向位移为14.5 mm，孔洞内贯穿钢筋达13.2 mm，混凝土块体位移仍较小；应力方面，构件均处于较高应力水平，开孔钢板周围应力达到了346 MPa，孔内贯穿钢筋也已经屈服，混凝土块仍处于低应力水平状态。非线性阶段荷载-位移全过程曲线如图9所示。

图9 非线性阶段荷载-相对位移全过程曲线

由此可见，随着位移荷载增大，混凝土隼逐渐被拉裂，结构进入非线性阶段，则可分为两个部分，第一部分由混凝隼抗剪和钢混粘结主导，第二部分混凝隼抗剪和钢混粘结破坏后，由贯传钢筋主导，当位移荷载继续增加，钢筋进入屈服，最终破坏表现为贯穿钢筋弯剪破坏，为典型的延性破坏，如图10所示。

图10 粘结标准PBL型破坏形态

5 有限元结果与试验结果对比

由于篇幅有限，现仅列出PS-B-R纯隼型和PB-B-C粘结标准PBL型的有限元与试验荷载-相对位移全过程曲线对比，分别见图11和图12。

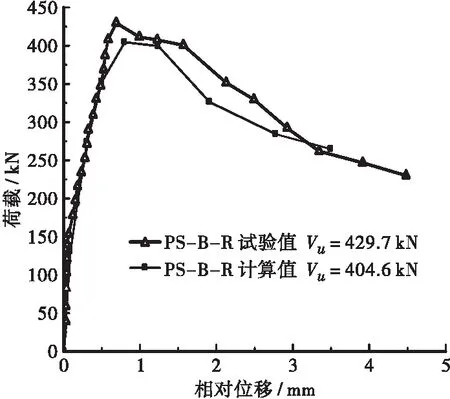
图11 PS-B-R荷载-相对位移全过程曲线对比

图12 PB-B-C荷载-相对位移全过程曲线对比

为直观地将有限元结果与试验进行对比，根据PBL键荷载位移全过程曲线，分别对其静力特性作如下定义：抗剪刚度Ks和使用状态承载力V0分别取相对位移为0.2 mm处的割线斜率和荷载；极限位移Vu和极限荷载δu分别取其最大荷载和对应位移；延性系数Dc为δu与0.02比值。静力特性定义如图13所示。

图13 静力学特性的定义

由表2有限元计算值与试验值静力学特性对比可知，按本文计算方法得出的抗剪刚度Ks、使用状态承载力V0和极限承载力Vu与试验值吻合度较好，其中，抗剪刚度、使用状态承载力试验值与计算值的比值平均值为1.02，标准差为0.10；极限承载力试验值与计算值的比值平均值为1.06，标准差为0.06。

因此，在不具备试验条件下，可采用本文数值分析方法确定PBL键静力学特性。总体上，标准型PBL键承载力、延性等各静力特性均优于纯钢筋、纯隼剪力键，采用高性能材料RPC替代混凝土浇筑的剪力键承载力和延性等静力特性更优。

但极限位移和延性系数计算值与试验值相差较大，主要原因可能为：混凝土隼被剪坏，抗剪作用转由贯穿钢筋承担时，混凝土隼产生了较大的塑性变形，部分单元畸变过度，迭代过程不平衡力无法消除。材料差异、施工随机性等也容易导致计算值与试验值存在差异。

表2 计算值与试验值静力学特性对比Table2 Comparisonofstaticcharacteristicsbetweencalculatedandexperimentalvalues试件Ks/(kN·mm-1)V0/kNVu/kNδu/mmDctct/ctct/ctct/ctct/ctct/cPS-B-R1036.0975.71.06207.2195.11.06429.7404.61.060.70.80.853.44.00.85PR-B-R1012.01002.61.01202.4200.51.01409.1351.51.165.95.21.1429.626.01.14PB-UB-R1349.91252.91.08270.0250.61.08551.4545.61.0118.815.01.2694.275.01.26PB-UB-C1354.91112.21.22271.0222.41.22530.3500.51.0617.310.51.6486.352.51.64PB-B-R1213.61388.10.87242.7277.60.87677.2697.70.9718.58.22.2692.540.92.26PB-B-C1136.21265.70.90227.2253.10.90596.0550.71.0817.77.22.4588.336.02.45平均值μ——1.02——1.02——1.06——1.60——1.60标准差σ——0.10——0.10——0.06——0.62——0.62注:t表示试验值,c表示计算值,由于纯粘结型试件NJ-B-R/C未设传剪构件,脆性破坏,不对其进行分析。

6 结论

本文基于8组PBL键试件试验结果，采用ANSYS有限元方法进行数值分析，研究PBL键荷载-滑移、静力学特性及传力机理，并将计算结果和试验进行对比，主要结论如下：

a.在低荷载下结构局部进入了非线性阶段，但对整体结构线性特征影响不大，其抗剪作用由混凝上隼与贯穿钢筋共同承担，贯穿钢筋处于弹性阶段。

b.在非线性阶段可分为2个部分，第一部分由混凝隼抗剪和钢混粘结主导，第二部分混凝隼抗剪和钢混粘结破坏后，由贯传钢筋主导，当位移荷载继续增加，钢筋进入屈服，最终破坏表现为贯穿钢筋弯剪破坏，为典型的延性破坏。

c.按本文计算方法得出的抗剪刚度、使用状态承载力和极限承载力与试验值吻合度较好，在不具备试验条件下，可采用本文数值分析方法确定PBL键的静力学特性。

d.标准型PBL键承载力、延性等各静力特性均优于纯钢筋、纯隼剪力键，采用RPC替代混凝土浇筑的剪力键承载力和延性等静力特性更优。