基于欧拉放大和灰度均值差法的桥梁动态响应研究
郑佳艳,毛若愚,吴 桐,唐 亮,周志祥
(1.省部共建山区桥梁及隧道工程国家重点实验室,重庆交通大学,重庆 400074;2.重庆交通大学 土木工程学院,重庆 400074)
振动信息是桥梁结构的关键动态信息,是桥梁健康监测的重要数据[1-2]。结构系统的加载情况、边界条件和物理性质(如刚度)退化会引起振动的改变。基于振动的桥梁健康监测常使用动态特性,如固有频率、模态振型等来监测可能发生的损坏位置及程度[2]。目前,桥梁结构动态特性的获取和计算常采用的方法是布置相当数量的振动传感器,形成传感器网络来收集振动数据。传统的接触式传感器是指安装到结构特定位置的速度或加速度传感器,其目的是测量该特定点处的动态响应。其优点是局部灵敏度高,但存在安装可达性较差、周期性校准无法实施、使用寿命有限、后期维护困难等缺点。
随着摄像机设备的快速更新,一般的高清高速摄像机的影像质量以及帧数频率已经能够满足对于大型结构动态响应影像数据的采集,并且非接触式的振动测量方法能够避免一些上述缺点。常采用的非接触式动态测量方法有雷达遥感测量技术、光纤超声波传感器技术、激光测振技术等方式。如CHO[3]等就传统测量手段、激光多普勒振动计(LDV)、基于视觉的位移测量系统(VDMS)和光电位移计(ODM)在全新高速铁路桥负载情况下的位移测量进行了比较分析,阐述了上述方法的可行性。孟利波[4]等利用电子散斑干涉法与全站仪测量结果进行对比,证明了其方法的可行性。熊春宝[5]等分别就GPS和百分表实测两种位移测量方式进行了对比分析,结果表明两者的测量精度相当,测量结果满足要求。董少博[6]提出采用多模干涉光纤超声波传感系统用于桥梁动挠度非接触式监测。黄智德[7]等采用激光测振对拉索索力进行了测试,结果表明该方法与常规传感器测试结果一致。上述采用的非接触式测量方法可靠性较好,但测量设备相对昂贵,且操作技术要求高。
而摄影测量中常使用数字视频数据来进行高精度测量静态位移(场),其方法是利用数字图像相关或边缘检测来测量结构的变形。在桥梁工程领域,陈强[8]等采用基于车载近景摄影采集轨道数字图像的方式检测轨道线形。崔宗会[9]等提出了一种基于移动最小二乘算法拟合整像素位移求解亚像素位移的数字图像相关方法,该方法大大提升了计算效率和精度。徐昊[10]等利用无人机拍摄方式获取图像并结合计算机图像处理技术为高墩大跨度结构检测困难的问题提供了一种解决办法。但是借助无人机拍摄的方式目前尚且不能提供足够的分辨率来支持对结构振动进行量测。邵帅[11]等利用近景摄影技术对实验室钢桁桥获取了其加载周期全息变形并在此基础上利用全息变形数据进行了损伤识别,证明了全息数据的重要性和潜力。
该方法面对的问题是桥梁结构变形微小,直接通过视频或图像来获取结构的变形信息所要求的拍摄环境条件很高,且单单通过边缘轮廓线上的像素点来识别位移的精度较低,可靠性难保证。2012年国外学者WU H Y[12]提出了一种欧拉微动放大技术的计算机视觉技术,它能够对视频中的微小变动进行放大。BALAKRISHNAN G[13]等运用该方法通过揭示人体中血液颜色的微弱变化来测量人体脉搏。WADHWA N[14]等应用基于相位的欧拉放大算法实现了高空中塔吊的微小运动、相机的抖动等一系列微小运动的放大处理。该技术的本质是放大视频图像中指定带通范围内目标信号的幅值大小,从而可以将常规仪器设备和人眼无法识别的微小运动信号放大到可以观察和分析的程度。本文将利用欧拉影像放大技术和图像处理技术(边缘区域灰度差平均方法)来通过边缘图像灰度差值量化结构目标的振动信息,并且通过采用叠差和边缘像素平均的方法极大地降低了由于噪声等原因引起的系统误差。同时通过对实验室自锚式悬索桥的高速摄影测量计算结果与动态位移传感器以及振动传感器的实测结果数据进行对比分析,验证该方法的有效性和准确性。该方法为无损检测(NDT)和结构健康监测(SHM)提供一种新的非接触式传感器测量方法。
1 理论与方法
视频是由一系列图像按时间序列组成,因此视频具有两个域(空间域和时间域);空间域体现在亮度值在单个图像中的分配情况值,时间域则是图像在时间上的演变关系,并通过两者结合来合成视频。图像可以通过滤波器在空间域中分解成幅值和相位信号,类似于加速度计信号,同时可以由傅利叶或小波变换进一步获取代表视频的时变信号。同时数字图像常借助相机图像传感器测量的RGB(红-绿-蓝)颜色模式存储。并将称为强度I的单个灰度值分配给每个像素,其中0和255分别代表黑色和白色。根据RGB值,MATLAB利用线性组合计算I,消除色调和饱和度信息,同时保持亮度[15],其强度I的计算表达式为:
I=0.298 9R+0.587 0G+0.114 0B
(1)
式中:R、G、B分别为图像中红色、绿色、蓝色分量值。
1.1 欧拉运动放大
近年来,国外提出了一种欧拉运动放大算法,该算法能够放大视频中的微小变化[12]。该算法使代表视频中物体运动的信号可以被时频带通滤波、放大和重构成视频。本文采用基于相位的运动放大算法,其原理是使用复数域金字塔将视频信号分解为局部空间组的幅值和相位。局部空间相位信号被时间傅里叶分解成一系列的空间相位信号。正弦波代表谐波运动,然后对相位信号进行时域带通滤波、放大和重组,形成运动放大视频。其结果是:视频中的运动在指定的带通范围内被进行了放大处理,其余带通范围的信号则保持不变并与放大后的信号一并合成为放大后视频;其欧拉放大流程示意图如图 1所示。

图1 欧拉放大流程图
1.2 框选叠差理论
本文基于上一节介绍的欧拉放大方法获取目标结构微小运动的动态响应视频,并且采用了一种基于边缘区域灰度平均值叠差的方法来从视频中获取所需要的工程物理量如位移、频率等。如图 2所示,该方法实现的前提是假设在视频拍摄的短时间过程中影像产生的噪声值是一致的,即由视频分解后的每一帧图像中的噪声值大致是相等的,于是通过前后帧灰度平均值相减叠差的方式可以将噪声值进行抵消,仅保留图像因上下振动而产生的灰度值的相对变化量。

图2 灰度均值叠差示意图
为了进一步说明了通过图像灰度平均值叠差方法来获取挠度曲线的思路。如图3所示,该示意图以第三节实验对象(模型悬索桥)为背景制作,主梁实际图像区域灰度值区间在0~180之间,虚线表示沿时间轴的框选区域灰度值的灰度强度曲线I(x)。本文假设:背景是深色的,并且感兴趣的对象是浅色的,同时被观测的目标结构只在竖直方向产生位移。被监视区域像素的位置和大小为P(t,x)表示的灰色方块。随着目标结构的上下振动,不同框选区域对应的灰度均值也不相同。使得灰度均值在I(x)曲线上垂直变换。边缘区域灰度均值就是将图像边缘的一个框选区域的I(x)进行均值化处理,这不仅能大大降低由于图像边缘轮廓线模糊带来的识别精度低,误差大等问题,还能提高图像的信噪比。
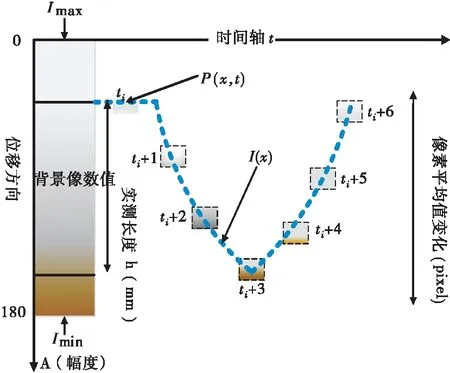
图3 灰度平均空域流程图
为了进一步阐明框选的功能及意义,如图 4所示,以Lt×Wt(像素×像素)大小作为目标结构整体视频区域,针对不同的视频可以框选不同大小如Lp×Wp(像素×像素)的边缘强对比度视频区域。在图像时间序列中该框选区域(Lp×Wp)的位置大小保持不变,而拍摄的目标视频区域(Lt×Wt)在激励后上下振动。同时依次把前一帧的像素灰度值作为参照值,进行前后帧图像灰度平均值叠差计算,计算得出灰度值的相对变化量。其中像素灰度函数为:

图4 灰度平均时域示意图
(2)
式中:IP(t)为图像区域像素灰度值;Imax,Imin为图像区域内像素最大值和最小值;np(t)为图像区域噪声像素值。
AP(t)=LP×WP是框选区域在时间序列上的像素灰度值之和,应该注意,框选区域的长度Wp(像素)应该足够大以保证图像振动产生的最大位移幅度A(像素)位于在框选区域之内,即框选边缘范围内主梁边缘不能离开该框选区域,满足Wp>A,避免关系变为非线性。
1.3 图像降噪处理
同时考虑到在实际的测量中始终存在噪声,本文用np(t)表示框选图像区域的噪声值。其定义如下:
(3)
其中,N是框选区域的像素总数;ni是像素i中存在的噪声。将式(2)的像素灰度值也进行平均化处理,其表达式为:
(4)
N是框选区域的像素总个数;Ii是像素i的灰度值。为了将像素灰度值与工程物理量挠度建立联系,需要进一步确定校准常数B(mm/pixel),如图5所示将观测到的灰度值与实际位移之间的对应关系,通过将框选范围的实际长度h(mm)除以从对应视频帧中相应长度范围的像素值Li来实现。即:
B=h/Li
(5)
对于相机视角不垂直于结构位移分量方向的情况,即当α≠0时,应用几何校正因子C(无量纲)。该因子计算如下:
(6)
其中,a、b分别为表示摄像机与目标中心之间的水平和垂直距离。
如图 5所示对于测试结构边缘区域,摄像机的垂直轴应与竖向坐标轴对准,同时角度β(表示相机与结构中心的水平偏差)对竖向振动测试的影响较小,因此忽略其对测试结果的影响。
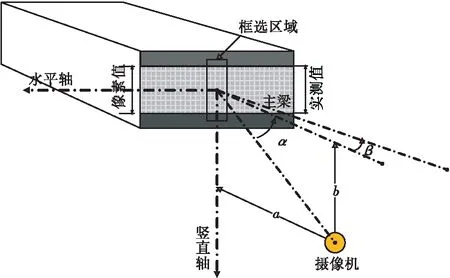
图5 主梁测量示意图
考虑到本文采用的欧拉放大技术对原视频位移具有放大作用,因此设置还原因子K,其值为欧拉放大因子的倒数。通过校准常数B和几何因子C以及还原因子K可以获得如下实际目标动态位移uact(t),mm:
uact(t)=B·C·K·Ip(t)
(6)
由于图像噪声的存在导致测试结果的误差加大以及测试精度降低,因此需要对图片进行降噪处理。本文采用叠差理论和像素平均方法大大降低了噪声对测试的影响。对于框选的边缘区域平均过程(在等式1和4中表示)本身有助于降低噪声,即噪声的功率直接随着框选区域中的像素数N的增加而减小。假设噪声是独立的,并且对于信号可以用静止过程表示,可以得到以下像素灰度值标准差的表达式:
(7)
从等式7右边的第二项可以看出,随着像素数量N的增加,噪声的功率随之降低;即标准差越小,数值结果就越集中,越接近平均值,表明由于噪声所引起的误差就越小。
在等式7中用Wp×Lp(图像框选区域的宽和长)代替N,即N=W×L(框选的宽度×长度),可以得到信噪比(SNR)的表达式为:

(8)
式(8)表明,为了达到最大信噪比,必须最大化WP-to-LP比值,即保持尽可能短的长度并且尽可能宽的宽度将使信噪比最大化,同时注意Lp应能覆盖最大位移幅度A。对于固定的相机和短时间的照明条件不变的条件下,可以假设像素噪声功率恒定,并且可以基于期望的信噪比指定适当的框选大小。式(8)中对信噪比另一个因素是Imax-Imin,它对信噪比有更显著的影响。从式(8)可知,目标中深色和浅色的对比度越高,信噪比就越高。
2 模型桥试验
2.1 试验概况
为了进一步的探索和论证基于欧拉影像边缘灰度平均差值的非接触式桥梁动态响应获取和结构位移测量方法在结构检测中的可行性和适用性,对室内一座自锚式悬索桥进行了试验研究。试验悬索桥为武西高速公路桃花峪黄河大桥缩尺模型桥,比例为1∶30。模型桥主跨13.534 m,边跨为5.3 m。该悬索桥的主梁为钢箱梁,桥道板为预应力混凝土桥道板,并且在跨中布置百分表测点,如图 6所示。

图6 实验室悬索桥设计图(单位:mm)
本次试验仪器有索尼FDR-AX700摄像机、百分表、东华DH3818Y静态采集仪、DH5902动态采集仪,各仪器设备布置如图 7所示。由于主梁结构与背景之间具备良好的色彩对比度即Imax-Imin的值较大,这有利于对结构的振动进行影像捕捉。为了证明该方法的有效性,试验大多是在理想的条件下进行,降低试验测试难度。并且考虑到悬索桥结构刚度小,柔性大的特性,仅在边跨位置施加一竖向冲击作用作为激励,使其产生自由振动,直至结构在阻尼效应下趋于稳定。

图7 悬索桥测试仪器布置图
2.2 数据采集与预处理
2.2.1数据采集
本次试验,采用索尼FDR-AX700摄像机获取桥梁结构影像数据,结合百分表和东华H3818Y获取主梁的挠度值,以及试验东华DH5902动态采集仪获取结构的基频信息。拍摄采用正交摄影的方式获取影像数据,拍摄帧速率为100 fps,该频率可以达到对该悬索桥结构的振动信号的获取要求。摄像机的位置垂直正交于试验桥梁,以降低角度效应引起的误差,并针对结构目标选择合适的拍摄距离,以避免重大的镜头畸变。
2.2.2数据预处理
首先对视频进行欧拉放大影像处理并获取悬索桥清晰的全息变形。同时为了展示欧拉放大处理后的视频效果,将视频图像进行了灰度处理:先将悬索桥的视频进行分帧处理,然后对分帧处理后的视频图像进行二值化处理,即将RGB图像转换为二值图像。处理后的图片仅保留悬索桥主梁区域为白色,其余区域转换成黑色。悬索桥主梁的二值图像如图 8所示。从图8可以清晰的看出,主梁在激励作用下产生的微小挠度变化能够被精确地捕捉并加以放大处理。

图8 二值化主梁变形示意图
其次,通过自主编写的Matlab软件程序对实验影像数据进行自动化的框选-分帧-均值化处理,其流程图如图 9所示。同时需要注意在主梁振动期间,框选的像素变化区域不得离开框选范围,避免引入非线性数据值,出现信号截波现象。对于不同区域的位移提取可以设置不同的框选位置,每一个框选区域可以被认为是放置在主梁上的“虚拟振动传感器”,从而为结构提供动态响应信号。这些振动信号的功能等效于传统的加速度传感器,可以获取到结构的动态响应,并适用于传统的时域-频域分析方法对获取的数据进行分析,得到结构的基频。
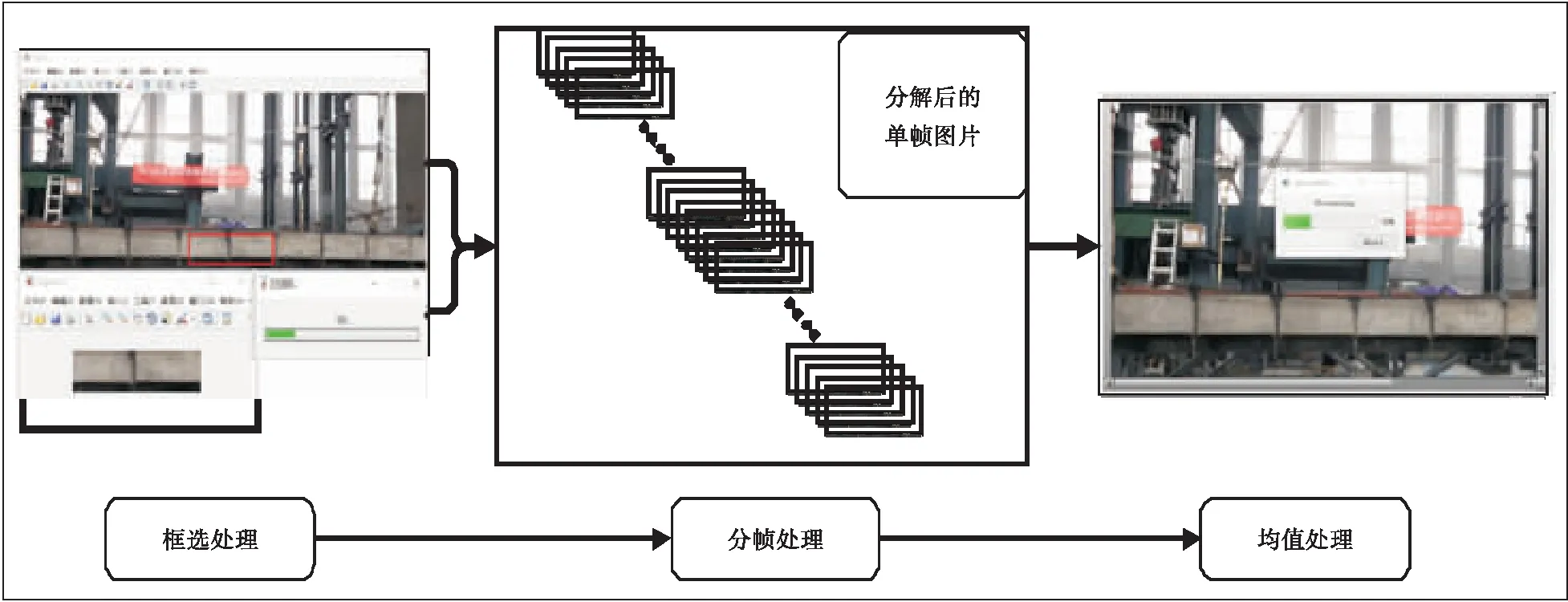
图9 框选分帧均值处理示意图
最后,如影像处理流程图10所示,将连续图像序列中前后帧图像像素灰度均值进行差值处理获取相对变化值,并考虑到桥梁在激励作用下,竖向挠度为其敏感性位移指标,因此获取了均值化处理后的悬索桥的动态响应原始信号数据,以及在各测点布置的动态百分表获取的对应实际挠度数据。为了比较2个测量结果的数据,采取2个步骤:①时域中信号的同步;②通过实际的校准因子B、还原因子K和几何因子C将像素灰度均值信号转换到实际位移。由于采用的正交摄影测量的方式(即摄像中心与目标中心保持一致即式(6)中几何因子C=1)。运用式(5)将位移信号转换为工程物理量(位移)。同时以组数据的峰值为统一指标,计算2个数据之间的时间延迟,并据此统一时间轴坐标。对上述2组数据进行相关性分析。并进一步对比通过傅里叶变化获取结构的动力特性参数(如基频)。直接采用振动传感器对实验室悬索桥进行测试获取相关动力特性参数。

图10 影像处理流程示意图
2.3 结果分析
经统一坐标后的位移实测值与像素转换值如图11所示,从图中可以看出由摄像机像素灰度值转化后的的位移曲线与实测位移在幅值较大阶段曲匹配较好。然而,随着振幅的衰减,误差逐渐加大,其原因可能是视频后期图像放大产生的误差带来的影响,且与百分表位移信号数据相比,相机信号显示的细节更少,噪音也更大。之后对两组数据进行了相关性分析,结果如图11中(b)所示,图中表明摄像机转换值数据和百分表获取的位移数据之间的相关性为0.979 7,其值接近于1,表明两组数据间的相关性高。
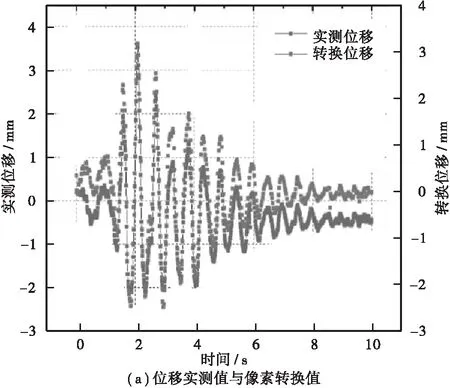
图11 归一化处理与相关性曲线示意图
之后对获取的视频图像边缘轮廓区域平均值时程曲线以及百分表实测挠度时程曲线进行快速傅立叶变换(FFT)频域分析,将获取结构的频率信息同通过加速度传感器实测的结构频率进分别对比分析,其结果如图12所示。结果表明通过基于欧拉放大的边缘区域灰度均值叠差方法所获取的结构基础频率为1.80 Hz与动态百分表实测挠度时间曲线经过傅里叶变化的计算结果1.76 Hz,以及振动传感器实测值1.76 Hz的差值均为0.04 Hz,相对误差仅为2.2%,相对误差产生的原因可能是由于图像精度、以及放大处理所引入的噪声所导致的。后期准备通过采用分辨率更高的摄像机,选择更加合适的放大因子等方式来增加数据的准确性。

(a)像素灰度值曲线
最终将3种数据获取方法得到的基频数据汇总:图像处理为1.80 Hz,位移实测为1.76 Hz,振动实测为1.76 Hz。结果表明本文提出的基于欧拉影像的边缘区域均值处理方法所获取结构的位移、以及基础频率信息是准确的。
3 实桥测试分析
3.1 实桥概况
为了评估该方法在实际环境中的适用性,本文还对重庆市的东水门大桥进行了视频图像信息数据采集和频率计算分析。东水门大桥为钢桁架梁斜拉桥,功能定位为公路与轨道两用,采用双向两车道,设计车速40 km/h;轨道交通设计时速60 km,主跨520 m,桥面宽21 m,全长1 000 m。
3.2 实桥测试
考虑到对任何的数字信号采样都需要满足采样定理即:采样率应不小于信号中可区分的最高预期频率的两倍,商用摄像机的帧速率在30、60和120 fps范围内,这对于测量大型结构系统(大型桥梁的基频一般为个位数)中的频率非常合适。因此本文采用100 fps的拍摄格式进行测试。同时针对过程中可能引入的噪声,本文采用了均值算法和叠差理论两种方式来进行处理,前者在像素点足够多时(N足够大)能够降低噪声带来的误差,后者通过前后图像叠差的方式来获取相对变化量从而减小噪声的影响。
3.3 结果分析
本文参考王涛[16]等提出了拉索振动测量相关概念以及方法。如图 13所示,对东水门大桥开展了现场影像拍摄,采用动态采集仪对拉索进行了现场实测,以第6根拉索为例,其实测一阶频率为:0.825 6 Hz,图像处理得到的基频值为:0.819 7Hz,两者的误差为0.059 Hz,这表明本文提出的方法具有较高的精度和可靠性。

图13 东水门拍摄示意图
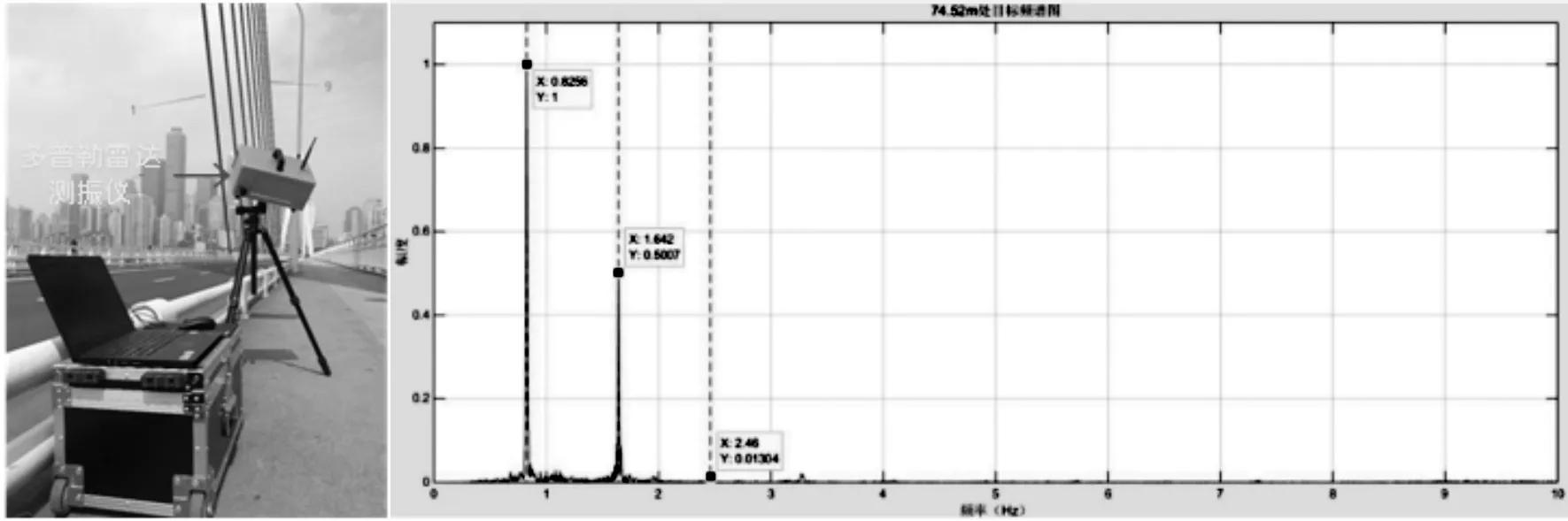
(a)拉索实测值
4 结论与展望
本文提出了一种结合欧拉微动视频放大技术和灰度均值差方法来获取桥梁振动信息,将高速摄像机作为非接触式的全场振动虚拟传感器,并通过该虚拟传感器获取结构的位移-时程曲线,计算了结构任意点的基频,在此基础上将影像数据计算的结果与实测结果进行对比分析,对比的结果包括转换后的位移-曲线、结构的基础频率。对比结果表明曲线吻合度较好,基频准确性高。因此,该工作为使用摄像机作为远程虚拟传感器测量相关参数提供了一种新的非接触式测量手段,并为进一步进行结构状态评估进行了前期的探索和准备工作。具体结论如下:
a.针对桥梁结构的低频振动特性,采用欧拉影像放大算法对指定带通范围信号进行放大处理,同时提出采用边缘区域像素灰度均值叠差的方法,通过前后帧图像像素灰度均值作差的方式来获取结构的绝对变化量,在有效获取到结构的变化信息的同时从而避免了利用图像边缘单个像素来进行位移信息提出所带来的偶然误差,且进一步降低视频影像信息中噪声的影响。
b.提出了采用高速摄像机作为结构振动频率的虚拟传感器,相比于传统的测量工具更加廉价、便捷,同时测量结果也具备较高的精度,满足工程测量的要求。证明了本文提出的方法能够有效获取结构的变形曲线以及任意区域的基础频率信息,为结构全息模态的获取提供了新的方法。
本文的结论都是基于场景中的光照保持不变的假设,这对于短时间测量而言容易满足,由于云层经过太阳或建筑物后而改变照明或背景条件,可能会在物体上引入错误的视频运动信号。同时测量的准确度取决于多种因素,如采样率、分辨率、量化噪声以及图像传感器质量和尺寸以及镜头类型,必须注意避免视频序列在这些条件下有太多的变化。若要将此方法进一步应用于结构的长期监测,则尚需对该方法进行深入研究,否则可能导致虚假的运动。

