基于灰色理论的中承式钢箱拱桥主梁线形控制研究

卓小丽, 王 华, 刘国坤, 田仲初

(1.广西交科集团有限公司, 广西 南宁 530007； 2.湖南省交通科学研究院有限公司, 湖南 长沙 410015;3.长沙理工大学 土木工程学院, 湖南 长沙 410114)

0 引言

随着我国交通建设的发展，钢箱拱桥因其施工便利、周期短、环保等特点在桥梁结构的应用中颇受推崇，已有诸多学者对钢箱拱桥的结构性能及结构设计方面进行了研究，刘中奇[1]以某三跨中承飞燕式钢箱提篮式拱桥为工程背景，利用钢箱拱桥Midas空间杆系模型以设计状态为基准对施工状态进行对比分析并不断进行动态调整指导施工，控制结果得到了良好成效；许颖强[2]等以湖北香溪长江公路大桥为背景对大跨度钢箱桁架拱桥拱肋架设施工技术进行了总结；周宇[3]等以广东揭阳市区进贤门大桥无推力中承式提篮拱桥为背景，通过实体和板单元模型对其静、动力性能进行了研究；陈耀章[4]等利用ANSYS建立了中承式拱桥钢锚箱式锚固结构的"实-壳"混合弹塑性有限元模型，并通过对加劲板和支撑板长度、承压板板厚等参数的敏感性分析，对中承式拱桥钢锚箱式锚固结构的受力机理进行了研究；张涛[5]等对成都某钢箱系杆拱桥进行了主梁温度场的测试，分别研究了钢箱梁温差变形对主梁线形控制的影响和墩部温差变形对线形控制的影响规律；田卿[6]等对汉口至阳逻江北快速路新河大桥中承式钢箱提篮拱桥进行了设计，并利用有限元分析验证了其安全可靠性；刘安兴[7]采用Midas分析软件对一大跨度下承式钢箱提篮拱桥进行了力学性能分析及参数研究，并利用ANSYS建立了拱脚局部实体模型进行了受力分析；江京翼[8]等对大跨径钢箱桁架拱桥稳定性及影响因素进行了研究分析，探讨了初始几何缺陷对大桥的线弹性失稳荷载的影响。近年来，灰色预测理论在桥梁监测及施工控制方面也得到了大量应用;胡斌[9]等以一大跨径悬臂浇筑施工刚构桥为工程背景，建立了GM(1，1)预测模型对施工过程中主梁线形预抬高值进行了预测，并利用实测数据进行了对比验证，分析了预测模型的精度及其影响因素；刘历波[10]等提出了一种基于马尔科夫链修正的灰色GM(1，1)理论模型——灰色-马尔科夫预测模型，并利用河北省数百座桥梁桥梁运营状况的数据与灰色GM(1，1)理论模型进行了对比验证分析，结果表明所提出的模型相较于灰色GM(1，1)理论预测模型具有更高的精度及稳定性；陈得意[11]等考虑异形拱桥拱肋旋转及轴线偏差，建立了空间异形拱桥拱肋线形MGM(1，2)预测模型，并通过实测数据验证了预测模型结果与实测数据吻合良好；哈娜[12]等针对桥梁结构的耐久性提出了灰色-马尔科夫组合模型进行了预测，并通过辽宁省某桥的实测对比验证了该模型的有效性。

基于以上研究成果，灰色预测理论在桥梁施工监测中的应用已逐渐崭露头角，但灰色理论在中承式钢箱拱桥主梁施工过程中的应用却鲜有报道。本文以广西柳州市官塘大桥中承式钢箱拱桥为依托背景，建立其节段施工考虑残差修正的GM(1，1)预抬高值预测模型，对灰色预测理论在中承式钢箱拱桥主梁施工线形控制中的应用展开研究。

1 工程概况

官塘大桥为中承式钢箱拱桥，计算跨径为457.183 m，计算矢跨比为1/4.5，净跨径为450 m，净矢高为100 m，拱轴线平面与水平面夹角为80°，拱平面与竖直平面的夹角为10°，钢箱拱肋截面宽度为5～5.012 m，截面高度为6.0～10.575 m，单个拱肋钢箱划分为27个吊装节段；拱肋采用一字横撑，横撑沿拱肋径向设置，全桥共计8道一字横撑；主桥吊索采用φ15.2 mm、270级环氧涂层钢绞线，单根直径15.22 mm，标准强度1 860 MPa，吊索采用整束挤压式锚具，材料选用40Cr；主梁为单箱单室扁平钢箱梁，吊索区桥面全宽为44.5 m，无吊索区桥面全宽为39.5 m，主梁截面中心梁高为3.5 m(外轮廓)，全桥钢箱梁划分为44个节段，编号分别为1#～44#；分为6类，A类梁段为端节段，共2段；B、C类为无吊索区段，共4段；D类梁段为过渡节段，共2段；E类梁段为标准段，共35段；F类梁段为跨中段，共1段。钢箱梁顶板及腹板厚为16 mm，底板及下斜板厚为12 mm。顶板在机动车道、非机动车道区域采用U肋进行纵向加劲，U肋上口宽为300 mm，底宽为170 mm，高为280 mm，板厚为8 mm，间距为600 mm。钢箱梁在端头靠近吊点的顶板区域(人行道区域)以及底板、下斜腹板均采用板式纵向加劲肋，加劲肋高为140 mm，板厚为12 mm，间距为350 mm。具体桥型布置图及横断面图如图1、图2所示。

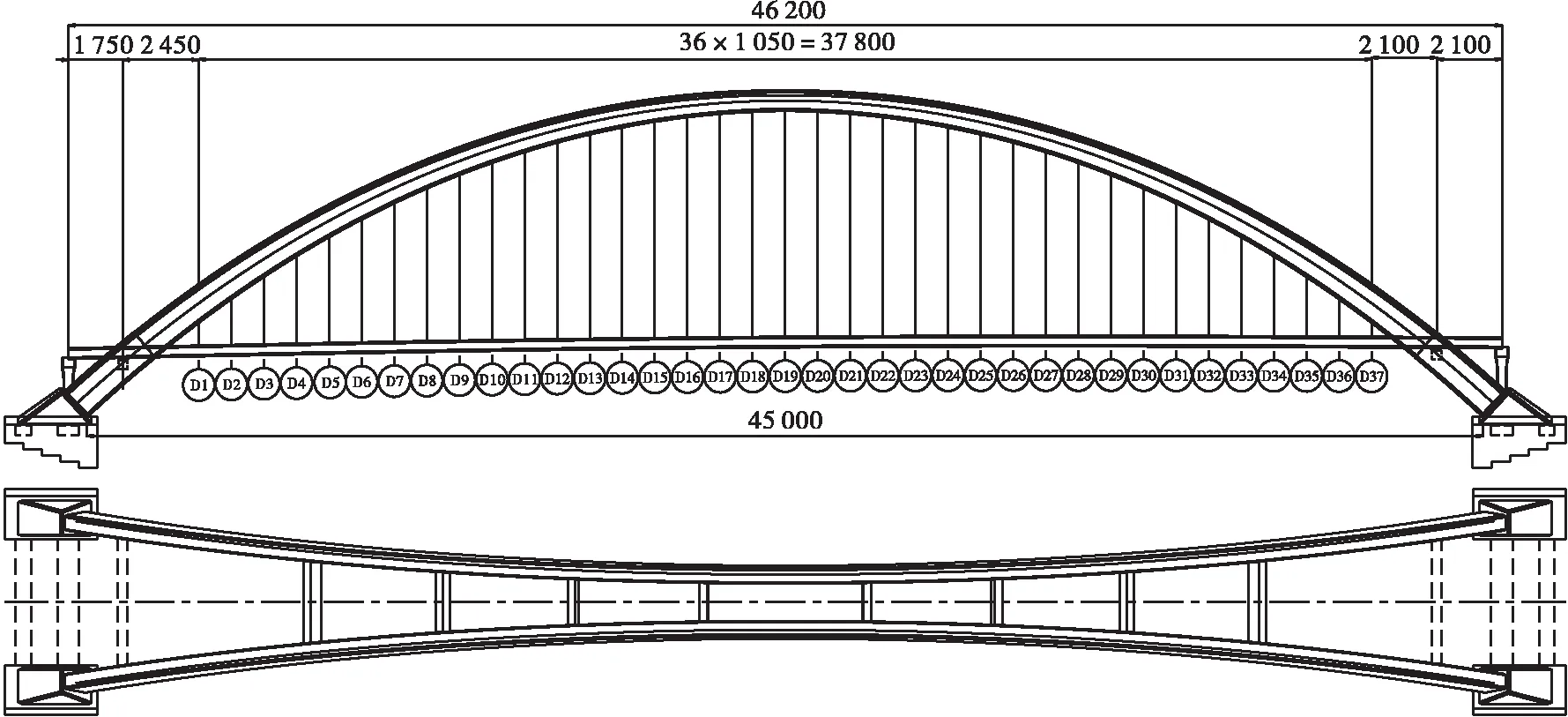
图1 官塘大桥桥型布置图(单位：cm)

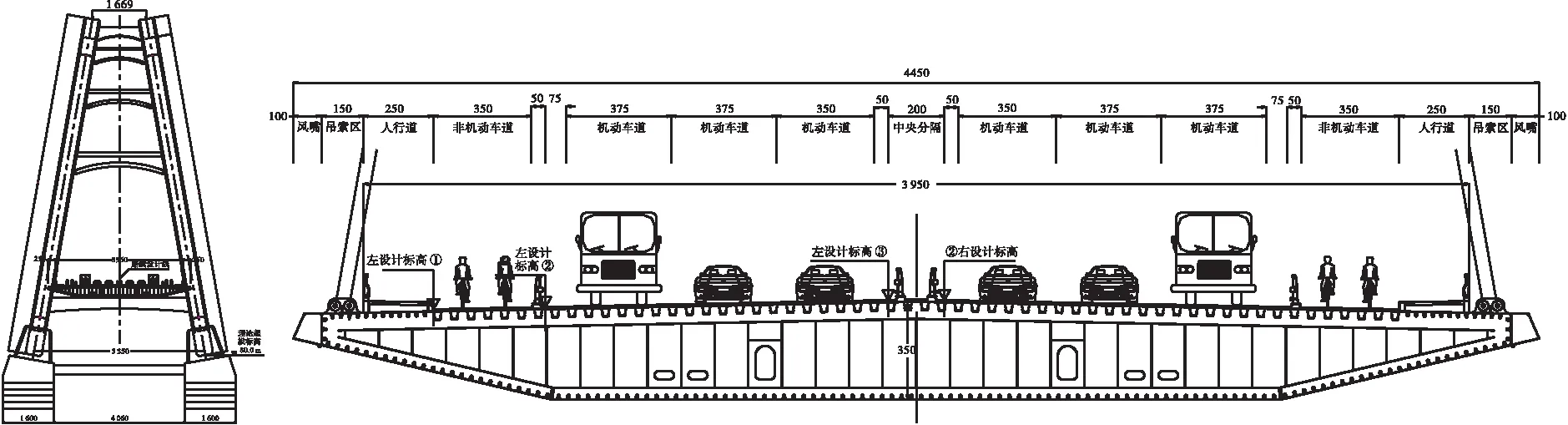
图2 官塘大桥横断面布置图(单位：cm)

2 灰色预测理论

2.1 GM(1，1)模型

我国华中科技大学邓聚龙教授于1982年提出了灰色系统理论，完全已知为白，完全未知为黑；而灰色系统则是部分已知、部分未知的系统。灰色方程称为GM模型，由Grey(灰)及Model(模型)的首字母缩写构成，G(1，N)前面的“1”代表模型阶数为一阶，后面的“N”代表模型包含N个变量，GM(1，1)模型则代表一阶单变量的微分方程模型。灰色方程GM(1，1)的具体建立过程如下。

给某一等时间隔的非负数据列{k，x(k)}：

{k，x(k)}=(1，x1)，

(2，x2)…(n，xn)

(1)

式中：k代表时刻；x(k)=xk代表t=k时刻时某量的观测值。非负数列x(0)代表某量的原始数据序列，如式(2)所示。

(2)

现对原始数据x(0)进行一次累加生成处理，如式(3)所示。

(3)

得到原始数据序列一次累加生成数据序列为X(1)：

(4)

经原始非负数据序列一次累加所生成的累加数序列X(1)具有更强烈的单调性。能近似看做是指数的，可通过指数型曲线进行线形拟合。现利用指数曲线来拟合具有强烈单调性的累加生成序列X(1)，则一定可以用某一阶线性常系数微分方程来表示这条指数拟合曲线：

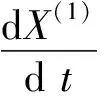
(5)

则有：

(6)

即:

(7)

(8)

Δt代表时间间隔，并认为时间可被充分细化，现将时间间隔Δt当成单位时间间隔。则有：

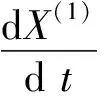
(9)

故式(5)可近似为：

x(0)(k+1)+aX(1)(t)≈u，(k≤t≤k+1)

(10)

式(10)中函数X(1)(t)为对应区间[k，k+1]上的某一取值，并用区间中值近似表达有：

(11)

则式(5)最终可近似简化成式(12)：

(12)

由式(12)可看出，该式为关于待确定参数a和u的一个线性近似表达式。故数据点(xi，yi)由式(12)可转化为：

yi≈axi+b

(13)

根据最小二乘原理，a和b作为线性回归系数可按式(14)进行求解：

(14)

式中：

(15)

由式(15)可知，当有n个原始数据时，则有n-1个依次累加而生成的数据。

最终有一阶微分方程的解为：

(16)

式(16)就是最后得到的预测模型，该模型称作GM(1，1)预测模型。上述各式中a代表了GM(1，1)模型发展系数，反映了x(0)和X(1)的发展态势；u代表了灰色作用量，反映了数据变化的关系。

则还原值：

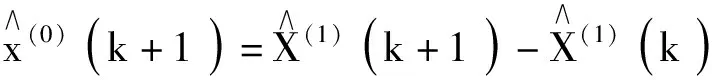
(k=1，2，…，N)。

2.2 残差GM(1，1)模型

当GM(1，1)模型精度尚未达到精度要求时，可通过残差序列建立GM(1，1)模型对原有GM(1，1)模型进行修正。

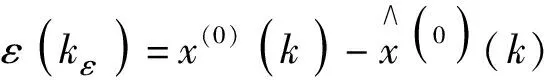
同式(5)有：

(17)

其时间响应式为：

(18)

e[-aε(kε-1)]，kε≥1

(19)

还原式残差修正模型如式(20)所示：

(20)

3 灰色预测模型的建立

3.1 初步预抬高值的预测

广西柳州市官塘大桥中承式钢箱拱桥主梁施工时的理论立模标高仅仅为理论分析计算模型数据，而因现场实际施工时的立模标高需考虑更多不确定因素，例如温度、施工荷载、弹性变形、天气及焊接工艺等；故理论分析计算值与现场实测数据有些许差异，需对理论立模标高进行适当修正。

令实测预抬高值序列为：Y=[Y(1)，Y(2),…，Y(N)]；令理论分析预抬高值序列为：Y′=[Y′(1)，Y′(2)，…，Y′(N)]；式中N为主梁施工阶段数。灰色模型误差X(0)(k)=Y(k)-Y′(k)+C;k=1，2，…,k，N，C=max|Y(k)-Y′(k)|。根据Y、Y′建立其灰色模型误差序列：X(0)=[X(0)(1)，X(0)(2)，…，X(0)(N)]。

(21)

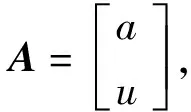
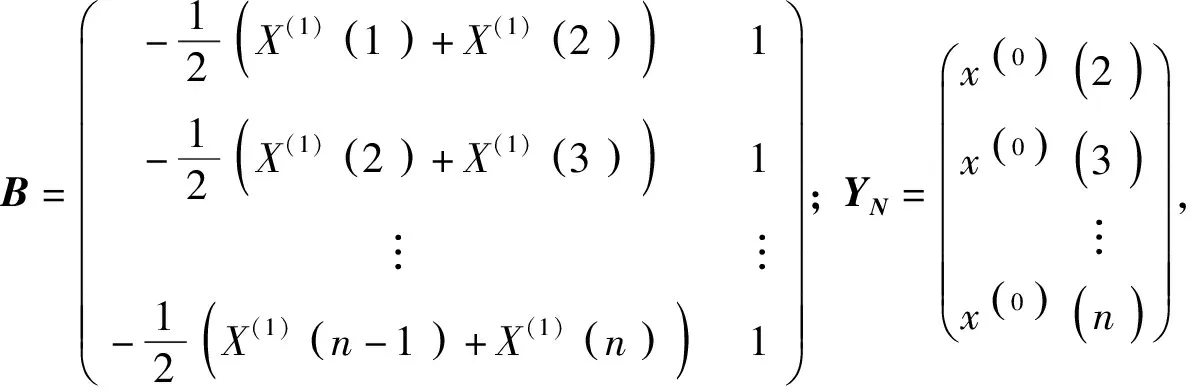
3.2 残差GM(1，1)模型预抬高值修正预测

根据2.2节有：

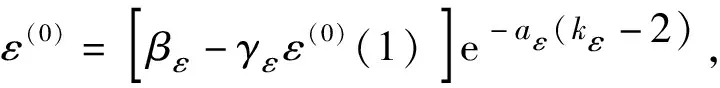
(22)

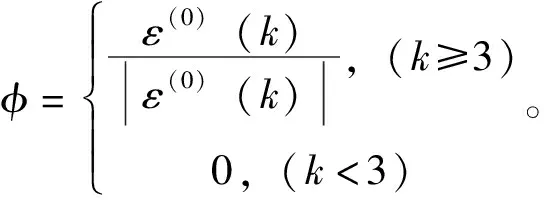
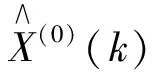
(23)

3.3 各主梁节段立模标高的确定

由前述3.1、3.2综合可得，经残差修正过后第k个主梁节段的立模标高如式(24)所示：

(24)

基于上述计算流程，根据理论分析计算预抬高值及现场实测数据，采用MATLAB编制广西柳州市官塘大桥主梁施工过程的立模标高灰色预测模型计算程序，预测主梁安装下个节段的立模标高，具体分析流程图见图3。

图3 主梁节段立模标高灰色预测模型计算流程图

4 有限元模型的建立

为研究灰色中承式钢箱拱桥主梁施工线形控制中预测理论的应用，以广西柳州市官塘大桥中承式钢箱拱桥为依托背景，建立了结构有限元仿真计算分析模型，通过有限元仿真计算分析模型求得官塘大桥主梁施工过程中各节段理论预抬高值，模型共划分为453个单元，520个节点，采用梁单元来实现主梁及肋间横撑的模拟，采用仅受拉桁架单元来进行吊杆的模拟；拱脚处采用固定约束，拱梁连接处采用弹性连接进行模拟；模型荷载作用考虑了结构自重、二期及施工临时荷载等，其中施工阶段临时荷载考虑了桥面吊机荷载，采用节点荷载进行模拟。相关材料参数表见表1，具体仿真计算分析模型如图4所示。

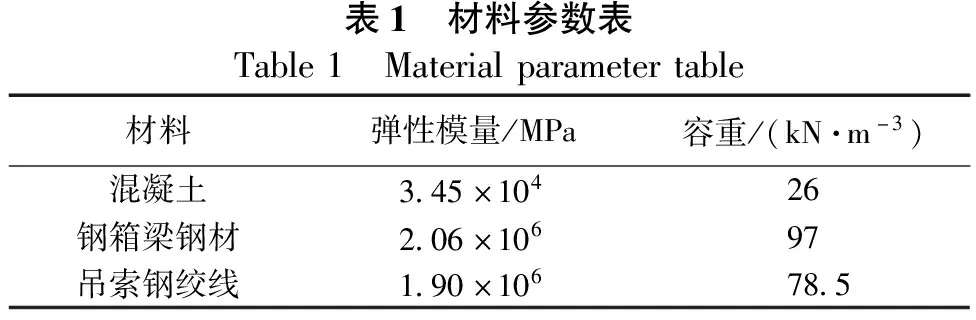
表1 材料参数表Table1 Materialparametertable材料弹性模量/MPa容重/(kN·m-3)混凝土3.45×10426钢箱梁钢材2.06×10697吊索钢绞线1.90×10678.5

图4 官塘大桥仿真计算分析模型图

根据上述所建立结构仿真计算模型，考虑主梁施工过程中各施工荷载因素得到了主梁各节段前端顶面中心施工阶段预抬值如表2所示。(仅考虑有吊杆的阶段即E类标准节段)

表2 主梁各节段施工阶段理论计算预抬值Table2 Theoreticalcalculationpre-liftvalueofeachsectionofthemainbeamduringtheconstructionstage节段号测点编号设计标高值/m预抬高值/mm节段号测点编号设计标高值/m预抬高值/mm 4# D1101.97018.524#D20104.953177.8 5# D2102.1809.925#D21105.008173.6 6# D3102.39013.626#D22105.055156 7# D4102.60012.727#D23105.092131.1 8# D5102.8118.828#D24105.121104 9# D6103.0137.129#D25105.14078.710# D7103.20713.230#D26105.15041.511# D8103.39125.231#D27105.15030.312# D9103.56743.332#D28105.14257.813#D10103.73367.933#D29105.12441.514#D11103.89096.934#D30105.09730.315#D12104.037126.535#D31105.06123.916#D13104.176151.636#D32105.01620.617#D14104.305165.637#D33104.96418.218#D15104.425163.538#D34104.91118.819#D16104.536141.639#D35104.85917.420#D17104.63899.740#D36104.80612.921#D18104.730132.641#D37104.80615.422#D19104.814165

5 灰色模型预测结果验证分析

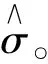
利用MATLAB编制的广西柳州市官塘大桥主梁施工过程的立模标高灰色预测模型计算程序以每4个节段滚动预测求解下一节段立模标高(即以k#～k+3#节段的理论与实测数据预测k+4#节段的立模标高)，并与节段施工完成后实测标高进行对比。立模标高的确定主要决定于节段预抬值的确定，现将8#～40#主梁预抬高值的预测结果及实测数据整理如表3所示。预测预抬高值与实测及理论预抬高值的对比曲线如图5所示。

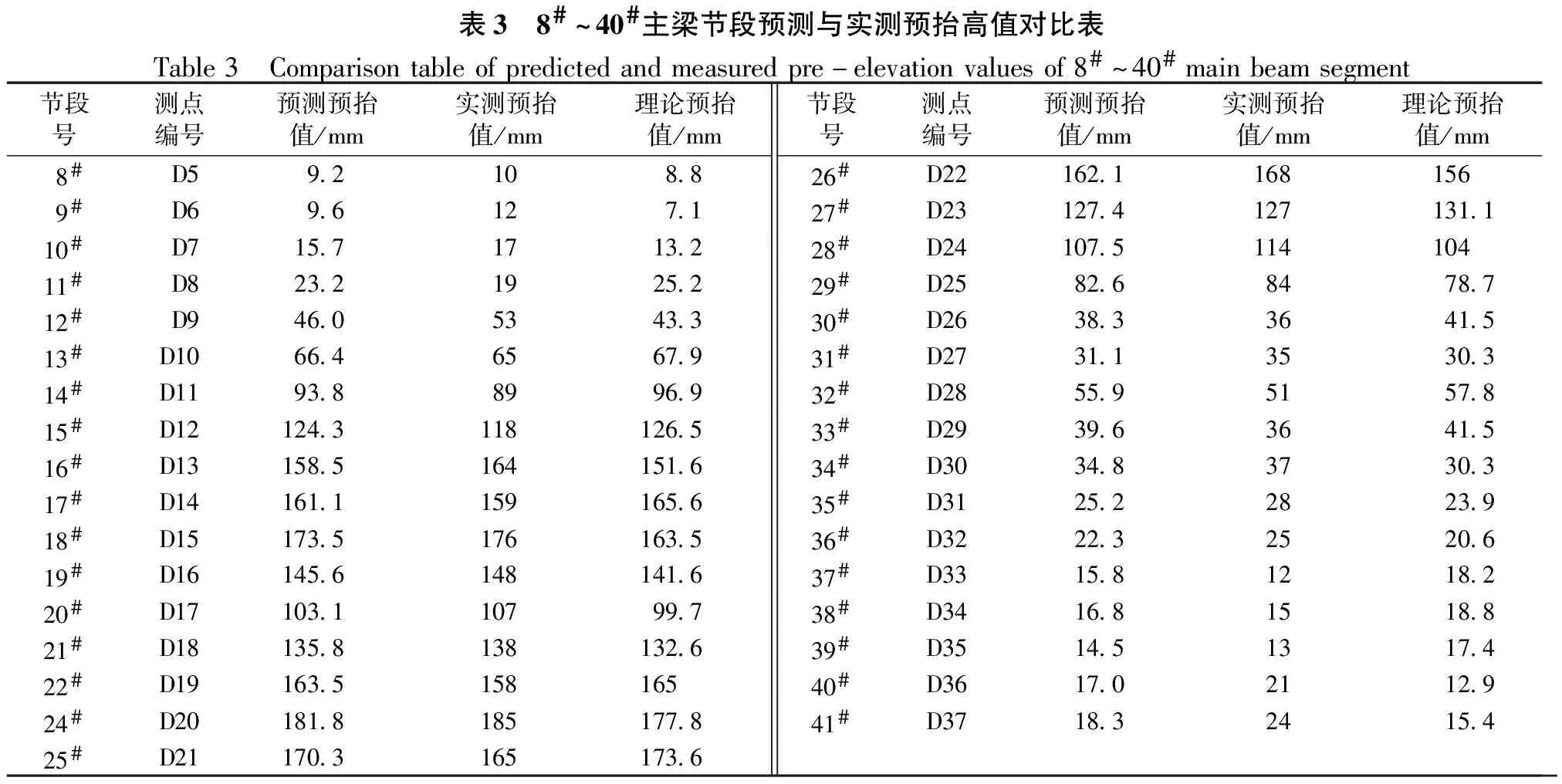
表3 8#～40#主梁节段预测与实测预抬高值对比表Table3 Comparisontableofpredictedandmeasuredpre-elevationvaluesof8#～40#mainbeamsegment节段号测点编号预测预抬值/mm实测预抬值/mm理论预抬值/mm节段号测点编号预测预抬值/mm实测预抬值/mm理论预抬值/mm 8# D59.2108.826#D22162.1168156 9# D69.6127.127#D23127.4127131.110# D715.71713.228#D24107.511410411# D823.21925.229#D2582.68478.712# D946.05343.330#D2638.33641.513#D1066.46567.931#D2731.13530.314#D1193.88996.932#D2855.95157.815#D12124.3118126.533#D2939.63641.516#D13158.5164151.634#D3034.83730.317#D14161.1159165.635#D3125.22823.918#D15173.5176163.536#D3222.32520.619#D16145.6148141.637#D3315.81218.220#D17103.110799.738#D3416.81518.821#D18135.8138132.639#D3514.51317.422#D19163.515816540#D3617.02112.924#D20181.8185177.841#D3718.32415.425#D21170.3165173.6

图5 预抬高值对比曲线表

由表3及图5分析可知，各节段实测预抬值与理论预抬值最大偏差(理论值-实测值)为-12.5 mm，最大偏差率[(理论值-实测值)/实测值×100%]为51.7%；利用灰色模型GM(1，1)滚动预测出的预抬值与实测预抬值的最大偏差(预测值-实测值)为-7 mm，最大偏差率[(预测值-实测值)/实测值×100%]为31.7%；预测预抬值与实测预抬值更接近，且各节段预抬值绝对误差不超过10 mm。经实测验证，考虑残差修正的GM(1，1)模型在广西柳州市官塘大桥主梁施工过程主梁线形预测效果良好，预测模型鲁棒性高。

施工过程中引入残差修正的GM(1，1)模型预测整个主梁(8#～41#)各节段立模标高，并严格控制主梁施工线形指导现场施工，现将成桥状态主梁理论线形、实测线形及预测线形对比图整理如图6所示。

图6 成桥状态主梁线形对比图

经对比分析有，成桥状态主梁实测线形与理论线形各节段最大偏差为34.5 mm，成桥状态主梁实测线形与预测线形各节段最大偏差为29.8 mm，由图6分析可知，主梁预测线形与实测线形吻合度高，验证了残差修正的GM(1，1)模型在广西柳州市官塘大桥主梁施工过程主梁线形预测的精度较高，可在中承式提篮拱桥钢箱主梁实际施工中推广使用。

6 结论

本文以广西柳州市官塘大桥中承式钢箱拱桥为依托背景，建立了考虑残差修正的主梁施工线形灰色预测模型GM(1，1)，并利用现场实测数据对模型进行了对比验证，研究了灰色理论在中承式钢箱提篮拱桥主梁施工过程中线形预测与控制中的应用。具体结论可总结如下：

a.主梁施工过程中预测预抬值与实测预抬值偏差最大仅7 mm，最大偏差率为31.7%;而实测预抬值与理论预抬值最大偏差为12.5 mm，最大偏差率为51.7%，预测预抬值与实测预抬值契合度高，精度良好。

b.成桥状态下主梁预测线形与实测线形吻合良好，相较于理论线形更为贴近，验证了考虑残差修正的灰色预测模型在中承式钢箱提篮拱桥主梁施工过程中应用的可行性及稳定性，可做推广使用。